论文学习—Model-based Adversarial Meta-Reinforcement Learning

Abstract

本文介绍了一种元强化学习（meta-RL）方法，即模型基础对抗元强化学习（AdMRL）。元强化学习旨在从多个训练任务中学习，以便于高效地适应未见过的测试任务。然而，现有的元RL算法在训练和测试任务分布不同时，性能可能会显著下降。

为了解决这个问题，文中提出了一种新的方法，AdMRL，它旨在最小化最坏情况下的次优性差距（即最优回报与算法适应后的回报之间的差异）。这种方法采用了基于模型的方法，并通过交替学习固定任务的动态模型和寻找当前模型的对抗性任务来优化它，即找到使模型导出的策略最大程度次优的任务。

这个方法采用了极小极大目标，假设任务家族是参数化的，通过隐函数定理推导出次优性梯度的公式，并展示如何通过共轭梯度方法和REINFORCE估计器高效实现梯度估计。最后，通过在连续控制基准上的实验，验证了该方法在所有任务上的最坏情况性能、对分布外任务的泛化能力，以及在训练和测试期间的样本效率，相较于现有的最先进元RL算法有所提升。

1. Introduction

1. 深度强化学习的挑战：虽然深度强化学习（Deep RL）技术能够解决复杂的问题，如围棋和Atari游戏，但这些方法通常需要大量的数据来训练，这意味着它们需要与环境进行大量的交互才能学习有效的策略。这在实际应用中可能是一个限制，因为在很多情况下，获取大量交互数据是昂贵或不可行的。

2. 元强化学习的目标：为了解决深度强化学习的采样效率问题，元强化学习（Meta-RL）应运而生。Meta-RL 试图通过在一组相关任务上学习来提高学习效率。具体来说，它旨在开发出能够迅速适应新任务的算法，即便是对于这些新任务只有非常有限的数据（即样本）。

3. 模型不可知元学习（MAML）：这是一种特定的元学习方法，它通过在训练期间学习一个可以快速适应新任务的策略初始化来改善采样效率。简单来说，MAML 旨在找到一种策略的初始设置，这样经过少量的调整，就可以快速适应新任务。

4. PEARL：这是更近期的一种方法，它不仅学习如何执行任务，还学习如何将任务表示在一个潜在的空间内，这样可以更有效地理解和适应新任务。通过这种方式，PEARL 能够在训练时识别任务的共性，并利用这些知识来更好地适应新的、未见过的任务。
   
   在传统的元强化学习框架中，训练任务和测试任务被假定为来自同一分布。这意味着，我们假设在训练时看到的任务类型和在测试时遇到的任务类型在统计上是相似的。这种假设有助于元学习算法通过在训练任务上学习，来更好地泛化到测试任务上。

然而，现实情况中，测试任务往往与训练任务在分布上有所不同。这种情况被称为“分布偏移”。当发生分布偏移时，即测试任务的分布与训练任务的分布不一致，现有的元RL方法的性能可能会显著下降。这是因为算法可能过度适应了训练任务的特定分布，导致它无法有效地适应与训练分布显著不同的新任务。

这个问题的核心是元学习算法的泛化能力——即算法适应新任务的能力在面对与训练过程中不同分布的任务时可能会下降。这一点对于设计能够在现实世界中广泛应用的强化学习算法尤为重要，因为现实世界的任务很少会严格遵循训练期间的分布。

上述讨论了PEARL（一种元强化学习算法）在处理具有不同速度目标的任务时的性能表现，特别是在二维蚂蚁速度任务（Ant2D-velocity tasks）上的应用。

1. 任务说明：这里的任务是让一个二维的蚂蚁（一个机器人或模拟体）达到指定的速度（x,y）。不同的任务由不同的目标速度定义，这些速度在一个二维空间内变化。

2. 训练和测试的分布：在训练期间，这些任务是均匀选取的，覆盖了速度的一个范围（从图中的[-3, 3]^2可以看出）。这意味着训练任务尝试覆盖了一个广泛的速度组合。

3. 性能评估：图1展示了PEARL在这些不同速度任务上的性能。性能是通过子最优性差距（sub-optimality gap）来衡量的，即任务的最优回报减去PEARL获得的回报。图中的颜色表示了这个差距：颜色越浅表示差距越小，性能越好。

4. 性能差异：PEARL在处理低速度目标的任务时表现更好（即能更好地适应这些任务），而在高速度目标的任务上表现不佳。这意味着，如果测试任务主要是高速度任务，那么PEARL的总体性能会下降，因为它在这些任务上的子最优性差距较大。

5. 解决方案：为了解决这个问题，Mehta等人提出了一种方法，通过迭代重新定义任务分布，使算法更多地关注较难的任务。这种方法旨在改善算法在更广泛的任务分布上的性能，特别是在它原来表现不佳的那部分任务上。

这段文字提出了一种对抗性元强化学习（adversarial meta-RL）问题的非分布式（non-distributional）观点。这里是如何理解这段内容：

1. 非分布式观点：传统的元强化学习（meta-RL）方法通常假设训练和测试任务来自同一分布。相比之下，非分布式观点不依赖于任务来自相同分布的假设。这意味着，即使测试任务与训练任务分布不同，这种方法也试图保持有效。

2. 对抗性元强化学习问题：在这种设置中，问题被构建为一种对抗性问题，其中算法试图最小化在最坏情况下的性能损失，即“最坏子优度差距”（worst sub-optimality gap）。这个差距是指算法在适应后与最优返回（即最佳可能性能）之间的差异。

3. 最小化最坏子优度差距：目标是在所有可能的任务中找到一种策略，使得在最困难的任务上的性能损失最小。这是通过优化算法的参数来实现的，例如共享的策略初始化或共享的动态（即算法在处理不同任务时使用的共同规则或模型）。

4. 极小极大问题：这个问题可以被数学上构造为一个极小极大问题（或两玩家游戏），其中一个玩家（最大化玩家）尝试选择最困难的任务（即使算法的性能最差的任务），而另一个玩家（最小化玩家）则尝试调整算法的参数以最小化在这个最困难的任务上的性能损失。这是一种策略和反策略之间的对抗，旨在提高算法对未知和挑战性任务的适应能力。

这种方法试图通过准备算法应对可能的最坏情况，从而提高元强化学习算法的泛化能力，特别是在面对分布偏移时，即当遇到的新任务与训练任务明显不同时。这种对抗性设置帮助确保算法能够在各种不同的任务上保持较好的性能，而不仅仅是那些与训练时相似的任务。

1. 基于模型的方法：这种方法依赖于在训练期间学习一个共享的动态模型。这意味着，无论面对哪个任务，算法都使用相同的基本物理或环境规则（即“动态”）作为学习的基础。这种模型可以捕获环境如何响应不同的行为，从而可以在测试时用于新任务，即使这些新任务在训练时未出现过。

2. 学习共享动态：通过学习在所有训练任务中通用的动态模型，算法可以更好地泛化到新任务，即使这些新任务的最佳策略与训练任务中的策略大不相同。这是因为，尽管任务的目标（如奖励函数）可能变化，但任务背后的基本物理规则或动态保持不变。

3. 样本效率：基于模型的方法在样本效率上通常优于无模型方法，尤其是在单任务设置中。样本效率是指算法从有限的交互数据中学习的能力。在元强化学习设置中，这种效率尤为重要，因为目标是快速适应新任务。

4. 对抗性训练：文中提到的“自然对抗性训练”指的是一种特定的训练过程，在这个过程中，算法在任务级别上进行优化，以最小化子最优性差距（即算法性能与可能的最佳性能之间的差距）。这涉及到一种动态的调整过程，其中算法试图找到最困难的任务（最大化子最优性差距），然后调整其参数以最小化这些任务上的差距（最小化子最优性差距）。

5. 极小极大优化：这里的方法涉及一种极小极大策略，即在参数化的动态上最小化子最优性差距，同时在参数化的任务上最大化它。这意味着算法不仅要学习如何在特定任务上表现得很好，还要学习如何在可能遇到的最困难的任务上表现得足够好。

综合来看，这种基于模型的方法利用了任务之间共享的动态，通过对抗性训练在元强化学习框架中提高泛化能力和样本效率。

上述讨论的是在元强化学习中针对任务参数进行优化的技术挑战和解决方案：

1. 技术挑战：主要的技术挑战在于如何以样本高效的方式优化任务参数。这里的“子最优性差距目标”依赖于任务参数，并且以一种非平凡的方式进行，因为算法在测试时间的适应阶段会反复使用这些任务参数。简单地通过算法的适应阶段的顺序更新进行反向传播是非常耗时的，尤其是在基于模型的方法中，尽管它们是样本高效的，但计算上仍然非常昂贵。

2. 解决方案的启发：受最近在监督学习中学习平衡模型工作的启发，作者提出了一种有效的梯度计算公式，该公式是相对于任务参数的，并且通过隐函数定理来实现。这种方法允许他们高效地计算梯度，即使在面对复杂的任务参数时也是如此。

3. 梯度计算：所提出的梯度计算方法涉及到逆海森向量积（inverse Hessian vector product）。这是一种高级的数学技术，可以用来高效地计算在优化问题中需要的梯度。通过使用共轭梯度方法和REINFORCE估计器，这一过程可以更加高效和实用。

4. 含义：通过这种方法，可以在元强化学习设置中更高效地优化任务参数，即使是在需要进行大量适应的情况下。这对于提高算法的实际应用和扩展性至关重要，因为它减少了计算成本，同时保持了样本效率。

这段描述涉及到在元强化学习中如何高效解决基于任务的参数优化问题，尤其是在算法需要在测试阶段快速适应新任务的场景中。通过使用高级数学技术，如隐函数定理和逆海森向量积，以及有效的估计方法，如共轭梯度和REINFORCE估计器，可以使这个过程更为高效和可行。

主要贡献：

1. 极小极大公式的提出：作者提出了一种基于模型的对抗性元强化学习（AdMRL）方法，并采用了极小极大（minimax）公式来解决分布偏移问题。在这种公式中，算法试图找到最优策略，以应对可能出现的最困难的任务（即“最大化”部分），同时调整模型参数以最小化这些情况下的性能损失（即“最小化”部分）。这种方法旨在提高算法在面对不同于训练分布的新任务时的适应能力。

2. 梯度估计的导出：他们开发了一种新的方法来估计相对于任务参数的梯度，并且展示了如何在样本和时间上高效地实现这种估计。这意味着他们找到了一种更有效的方式来调整任务参数，以改进学习过程，从而使训练和适应新任务更加高效和有效。

3. 性能的显著提升：他们的方法在多个方面显著优于现有的最先进的元强化学习算法。具体来说，他们的方法在所有任务的最坏情况性能、对于分布外任务的泛化能力，以及在训练和测试时的样本效率方面，都显示出了显著的改进。这意味着他们的算法不仅能够更快地适应新的、未见过的任务，而且在面对极端或不利情况时也能表现得更好。

总之，这篇论文提出了一个新的元强化学习框架，通过对抗性训练和极小极大优化，显著提高了元强化学习算法在处理分布偏移和新任务适应性方面的能力。这对于开发能够在现实世界中广泛应用的强化学习算法具有重要意义。

2. Related work

1. 两种主要方向的元学习方法:

   • 预测新任务的最佳基础学习者：这种方法涉及训练一个元学习者（meta-learner），它能预测对于新见任务最有效的基础学习者（base learner）。这意味着元学习者学习如何根据新任务的特征快速定制或选择一个特定的学习策略或模型。
   • 更新基础学习者以快速适应新任务：这种方法集中在直接调整基础学习者的参数，以便它们可以更快地适应新的任务。MAML是这个方向上的一个经典例子，它通过少量步骤内的调整使基础学习者能够迅速适应新任务。

2. MAML（Model-Agnostic Meta-Learning）：

   • MAML旨在发现一组初始参数，这组参数能够使基础学习者通过少量的学习步骤和样本数据迅速适应新任务。MAML的关键在于其模型不可知性，意味着它可以应用于多种不同类型的模型和任务。

3. 提高样本效率的方法：

   • GMPS（Guided Meta-Policy Search） 和 **VaribAD（Variational Bayes-Adaptive Design）**等方法尝试通过不同策略改进样本效率和适应性。例如，GMPS可能通过将策略条件化在任务的潜在表示上来改善适应性，而VaribAD通过合并多个策略的解决方案来提高样本效率。
   • 这些方法试图解决传统元RL方法中存在的样本效率低下问题，即如何在有限的交互下快速学习新任务的最佳策略。

4. 对抗性训练和动态模型适应：

   • 一些方法提出使用对抗性训练来使元学习算法能够更好地处理任务间的分布偏移，即训练和测试任务的差异。这涉及到在训练过程中故意引入难度较大的任务，使得学习算法不仅能适应常见的任务，也能适应更异常或更具挑战性的任务。
   • 同时，通过动态模型适应（比如通过改进的信用分配或通过模型的动态调整），算法可以更灵活地适应新环境，提高其泛化能力。

1. 基于模型的强化学习（MBRL）的优势：MBRL被认为是减少强化学习算法样本复杂度的有希望的途径。相较于直接从与环境的实际交互中学习（即模型无关的方法），MBRL通过学习环境的模型来预测未来的状态和奖励，从而可以在没有实际执行动作的情况下进行策略的测试和改进。

2. Dyna风格算法：这是MBRL的一个流行分支，由Sutton等人提出。Dyna风格的算法通过交替执行两个主要步骤来工作：首先，收集实际环境中的样本来更新模型（即学习环境的动态）；然后，使用这个学到的模型生成虚拟数据（或称为模拟数据），以此来改进决策策略。这种方法的优点是它结合了真实环境数据的学习和通过模拟获得的数据来快速改进策略，从而减少了实际交互的需要。

3. 基于模型预测控制（MPC）的方法：MPC是另一种MBRL的方法，它在每个时间步使用学习到的模型来进行短期规划，并选择动作。在MPC中，模型用于预测未来的状态，基于这些预测，算法评估不同动作的后果，并选择预期效果最好的动作。MPC特别适用于需要连续决策和快速反应的场景，因为它允许算法在没有实际执行之前，就通过模型预测未来的结果来“思考”多步前进。
   
   上述描述了所提方法与现有方法之间的联系和区别，特别是在探索和学习策略方面：

4. 与主动学习的关系：主动学习是一种机器学习策略，旨在主动选择最有用或最困难的数据点进行学习，以提高学习效率。这里提到的方法与主动学习相关，因为它也在尝试在任务空间中找到最重要的点，即它在寻找那些能最大化学习效率的任务。但不同的是，这里的方法专注于在任务空间而不是传统的数据空间进行操作，这意味着它试图确定哪些任务是学习过程中最关键的。

5. 与好奇心驱动学习的关系：好奇心驱动的学习依赖于内在的好奇心激励来鼓励代理在环境中探索。这与本文的方法相关，因为它们都鼓励探索，但本文的方法是在任务空间中进行“探索”，而不是在传统的状态空间中。这意味着，代理被鼓励去探索和学习不同的任务，而不仅仅是在一个给定任务内部的不同状态。

6. 与Jin等人的工作的对比：Jin等人的工作旨在为任何给定的奖励函数计算近乎最优的策略，通过充分探索来实现这一目标。而本文的方法不仅仅是寻找近乎最优的策略，而是寻找能够揭示最大子最优性差距（即学习潜力最大或最具挑战性的部分）的奖励函数。这表明，本文的方法不只满足于找到好的策略，而是通过识别和优化在最困难情况下的表现来提高整体学习和适应能力。

总的来说，这段文字强调了研究团队的方法如何结合了主动学习和好奇心驱动学习的概念，并将它们应用于任务空间探索，而不是传统的数据点选择或状态空间探索。此外，与现有方法相比，它在寻找具有最大子最优性差距的奖励函数方面采取了一种更主动和目标导向的方法。这种方法旨在改善代理在面对未知和复杂任务时的适应性和性能。

3 Preliminaries

这段文字是关于强化学习的基础知识，主要介绍了马尔可夫决策过程（MDP）和一些基本的概念。以下是具体的解释：

1. 马尔可夫决策过程（MDP）：考虑一个具有状态空间 $S$ 和动作空间 $A$ 的马尔可夫决策过程。在这个框架下，决策者（或学习代理）在每个时间点选择动作，并根据这些动作转移到新的状态。

2. 策略 $\pi (a|s)$：策略定义了在给定状态 $s$ 下采取动作 $a$ 的条件分布。简而言之，策略告诉代理在特定状态下应该采取什么动作。

3. 转移动态 $T(a|s,a)$：转移动态指定了在当前状态 $s$ 和采取动作 $a$ 之后转移到下一个状态的条件分布。这些动态通常是未知的，并且需要通过与环境的交互来学习。

4. 奖励函数 $r(s,a)$：奖励函数为每一步的状态-动作对定义了一个奖励，指导代理学习什么是好的行为。

5. 折扣因子 $\gamma$：折扣因子在 $[0,1]$ 范围内，用于计算未来奖励的当前价值，其中值越接近0意味着越注重即时奖励，而值越接近1则意味着未来奖励被考虑得更多。

6. 值函数 $V^{\pi ,T}(s)$：值函数定义了在策略 $\pi$ 和转移动态 $T$ 下，从状态 $s$ 开始的预期回报。值函数可以表示为期望的累积折扣奖励：$V^{\pi ,T}(s)=E[{\sum }_{t=0}^{\infty }{\gamma }^{t}r(s_t,a_t)|s_0=s]$。这是从状态 $s$ 开始并遵循策略 $\pi$ 时，代理可以期待获得的平均总回报。

7. 强化学习的目标：RL的目标是寻找一个策略 $\pi$，最大化预期返回 $\eta (\pi ,T)=E[V^{\pi ,T}(s_0)]$，其中 $s_0$ 是从初始状态分布 $p_0$ 中抽取的。这意味着寻找一个策略，它可以在给定的马尔可夫决策过程中获得最大的平均回报。

这段文字介绍了元强化学习（Meta-Reinforcement Learning, Meta-RL）的概念，并与标准强化学习（Reinforcement Learning, RL）进行了对比。以下是具体的解释：

在元强化学习框架中，我们考虑一系列的任务，这些任务通过参数集合 $\Psi \subseteq {\mathbb{R}}^k$ 来参数化。我们同样考虑一系列策略，这些策略通过参数集合 $\Theta \subseteq {\mathbb{R}}^p$ 来参数化。元强化学习的目标是学习一个策略，这个策略不仅在一个单一任务上表现良好，而且能够迅速适应一系列相关任务。

每个任务可以被看作一个马尔可夫决策过程（MDP），具有相同的状态空间 $S$、动作空间 $A$、转移动态 $T$，但有不同的奖励函数 $r_{\psi }$。每个任务由其奖励函数参数 $\psi$ 来唯一确定。

对于每个任务 $\psi$，策略 $\pi$ 在该任务下的价值函数被表示为 $V_{\psi }^{\pi ,T}$，并且每个任务的期望回报（或性能）被定义为 $\eta (\pi ,T,\psi )=\mathbb{E}[V_{\psi }^{\pi ,T}(s_0)]$，其中 $s_0$ 是初始状态分布。

为了简化，我们使用 $\eta (\Theta ,T,\psi )$ 作为策略参数集 $\Theta$ 在动态 $T$ 和任务 $\psi$ 下的期望回报的简写。

在元强化学习中，目标是利用跨任务的共享结构来快速适应新任务。这里介绍的共享结构 $\Phi \subseteq {\mathbb{R}}^d$ 是一组可以跨多个任务应用的特征或规则。

• 共享结构 $\Phi$：这是所有可能的共享结构的集合，元强化学习算法试图找到一个特定的共享结构 $\varphi \in \Phi$，这个结构能够帮助算法快速适应新的任务。
• 训练算法 $A:\Phi \times \Psi \to \Theta$：这是一个映射或函数，表示从共享结构和任务参数到策略参数的过程。简言之，它表示如何根据共享结构和特定任务信息来定制或调整策略。

基于模型的强化学习（MBRL）:

在MBRL中，重点是参数化模型的转移动态 ${\hat{T}}_{\varphi }$，这通常是通过神经网络实现的，以便模拟真实环境的动态 $T^{\ast }$。

• 转移动态 ${\hat{T}}_{\varphi }$：这是通过学习得到的环境动态的近似，其中 $\varphi$ 表示模型参数。MBRL的目标是调整 $\varphi$ 使得 ${\hat{T}}_{\varphi }$ 尽可能接近真实的环境动态 $T^{\ast }$。
• 随机下界优化（SLBO）：这是一种MBRL算法，它提供了策略改进和模型拟合之间的理论保证。SLBO通过交错地进行策略改进和模型拟合来确保单调提升，即保证策略的性能随着时间的推移逐步提高。

区别和联系：

与标准的强化学习相比，元强化学习通过学习能够跨多个任务应用的共享结构来提高学习效率和适应性。而基于模型的强化学习则专注于学习一个环境模型，以便在不直接与真实环境交互的情况下进行策略的评估和改进。

元强化学习和MBRL在一定程度上是互补的：元强化学习使得策略能够快速适应新任务，而MBRL则通过提供一个准确的环境模型来提高策略评估的效率和效果。在元强化学习中应用MBRL的概念，如通过共享结构来改善模型学习，可以进一步提升适应新任务的能力。

4 Model-based Adversarial Meta-Reinforcement Learning

4.1 Formulation

这段文字进一步细化了在元强化学习框架中考虑的任务族，特别是如何定义和计算任务的总回报。以下是具体的解释：

1. 任务族和奖励函数：考虑一个任务族，每个任务通过参数 $\psi$ 来区分，且每个任务都有其对应的奖励函数 $r_{\psi }(s,a)$。这些奖励函数根据任务参数 $\psi$ 来差异化，并且假设对于所有状态 $s$ 和动作 $a$，奖励函数关于 $\psi$ 是可微分的。这意味着可以通过改变 $\psi$ 的值来调整奖励函数，从而影响学习代理的行为。

2. 总回报的定义：策略 ${\pi }_{\theta }$ 在动态 $T$ 和任务 $\psi$ 上的总回报定义为 $\eta (\theta ,T,\psi )={\mathbb{E}}_{\tau \sim {\pi }_{\theta },T}[R_{\psi }(\tau )]$。这里，$R_{\psi }(\tau )$ 是在奖励函数 $r_{\psi }$ 下的轨迹 $\tau$ 的总回报，而期望是在策略 ${\pi }_{\theta }$ 和动态 $T$ 下关于轨迹 $\tau$ 的分布计算的。

3. 真实环境和虚拟动态下的回报：

   • 真实环境回报 ${\eta }^{\ast }(\theta ,\psi )$：它等价于在真实动态 $T^{\ast }$ 和任务 $\psi$ 下策略 ${\pi }_{\theta }$ 的期望总回报，即 ${\eta }^{\ast }(\theta ,\psi )=\eta (\theta ,T^{\ast },\psi )$。
   • 虚拟动态下的回报 ${\hat{\eta }}_{\varphi }(\theta ,\psi )$：这表示在学习到的（或估计的）动态 ${\hat{T}}_{\varphi }$ 和任务 $\psi$ 下策略 ${\pi }_{\theta }$ 的期望总回报，即 ${\hat{\eta }}_{\varphi }(\theta ,\psi )=\eta (\theta ,{\hat{T}}_{\varphi },\psi )$。

在元强化学习的背景下，这种设置帮助区分了代理在真实环境和在根据其学习到的环境模型（即虚拟动态）中的表现。通过比较 ${\eta }^{\ast }(\theta ,\psi )$ 和 ${\hat{\eta }}_{\varphi }(\theta ,\psi )$，我们可以评估学习到的动态模型的质量以及策略在新任务上适应的能力。

上述描述了元强化学习中的一个关键概念：在学习到的动态模型上执行零次模型基础适应，并定义了最差情况下的子最优性差距。以下是具体的解释：

1. 学习到的动态和测试任务：假设我们有一个通过参数 $\varphi$ 学习到的动态模型 ${\hat{T}}_{\varphi }$ 和一个测试任务 $\psi$。我们的目标是在这个学习到的动态下找到最佳策略，即 ${\text{argmax}}_{\theta }{\hat{\eta }}_{\varphi }(\theta ,\psi )$，这意味着我们想找到一个策略参数 $\theta$，它可以在模型 ${\hat{T}}_{\varphi }$ 和任务 $\psi$ 下获得最大的预期回报。

2. 子最优性差距 $\mathcal{L}(\varphi ,\psi )$：对于给定的动态模型 $\varphi$ 和任务 $\psi$，子最优性差距定义为在任务 $\psi$ 上的 ${\hat{T}}_{\varphi }$-最佳策略和最佳策略在真实环境中的性能之间的差距。形式上，它定义为真实环境中最佳策略的期望回报 ${\eta }^{\ast }(\theta ,\psi )$ 与在模型 ${\hat{T}}_{\varphi }$ 上找到的最佳策略的期望回报 ${\hat{\eta }}_{\varphi }({\text{argmax}}_{\theta }{\hat{\eta }}_{\varphi }(\theta ,\psi ),\psi )$ 之间的差距。

3. 最小最大问题：整体目标是找到一个共享的动态模型 $\varphi$，使得在所有测试任务 $\psi$ 上的最差情况子最优性差距 $\mathcal{L}(\varphi ,\psi )$ 被最小化。这可以通过解决以下最小最大问题来实现：
   $$\underset{\varphi }{\min }\underset{\psi }{\max }\left[\underset{\theta }{\max }{\eta }^{\ast }(\theta ,\psi )-{\eta }^{\ast }({\text{argmax}}_{\theta }{\hat{\eta }}_{\varphi }(\theta ,\psi ),\psi )\right]\equiv \mathcal{L}(\varphi ,\psi )$$
   这个公式表示我们首先寻找对每个任务 $\psi$ 最坏情况下的动态模型 $\varphi$（即使子最优性差距最大化），然后尝试找到使这种最坏情况下的子最优性差距最小的动态模型参数 $\varphi$。
   这段文字描述了一个针对元强化学习问题的优化流程，特别是在寻找最优动态模型参数 $\varphi$ 和任务参数 $\psi$ 以最小化最坏情况下的子最优性差距。以下是具体的解释：

   这里，$\mathcal{L}(\varphi ,\psi )$ 是定义为在给定模型参数 $\varphi$ 和任务参数 $\psi$ 下的子最优性差距。

4. 内部步骤（针对 $\psi$ 的最大化）：在内部步骤中，我们寻找最难的任务 $\psi$，使得在学习到的动态 ${\hat{T}}_{\varphi }$ 下最优的策略在真实的MDP中表现最差。这意味着我们试图找到一个任务，对于当前模型 ${\hat{T}}_{\varphi }$ 来说，基于该模型产生的最优策略与真实环境中的最优策略之间的性能差异最大。

5. 外部步骤（针对 ${\hat{T}}_{\varphi }$ 的最小化）：在外部步骤中，我们通过最小化最坏情况下的子最优性差距来优化动态模型 $\varphi$。这意味着我们试图找到一个模型参数 $\varphi$，使得在所有可能的任务 $\psi$ 上，这个参数能够最小化最优策略和模型生成策略之间的性能差距的最坏情况。

6. 算法目标：通过在最难的任务上训练，我们希望获得对改正模型不准确性最有信息量的数据。这种方法的思想是，通过解决模型在其表现最差的地方，我们可以最有效地改进模型，从而在广泛的任务上提高其性能。

总体而言，这种方法采用了一种系统的方式来确定在哪些任务上模型最需要改进，并通过改进这些领域来提高整体性能。这种最小最大问题的解决方案旨在找到一种平衡，使得学习到的模型能够在面对多样化和具有挑战性的任务时表现得更加鲁棒。

通过在元强化学习过程中，特别是在内部步骤中，对模型进行训练，我们专注于最难的任务，因为这被认为是提高模型准确性的最有效方式。

具体来说，"最难的任务"指的是那些在当前模型下，策略表现与在真实环境中理想表现之间存在最大差距的任务。这种任务通常会揭示模型的不足之处，因为模型在这些任务上未能准确预测环境的动态或未能生成有效的策略。

通过在这些最难的任务上训练，我们希望获得最能揭示模型错误的数据，因为这些数据能够直接指向模型预测与实际环境之间的不一致。从理论上讲，这可以帮助我们更有针对性地调整模型，从而减少这些不一致，提高模型的整体准确性和泛化能力。

总的来说，这种方法旨在通过有目的地集中在揭示最大错误的场景上，来更有效地利用有限的训练资源，进而更快地改进和适应模型。这是一种常见的策略，特别是在处理高度复杂和多变的环境时，如元强化学习场景所常见的。

4.2 Computing Derivatives with respect to Task Parameters

上述描述了如何优化元强化学习中定义的子最优性差距 $\mathcal{L}(\varphi ,\psi )$ 的问题，特别是通过交替使用梯度下降和梯度上升方法。这里是详细的解释：

1. 优化过程：为了优化等式 (1)，即最小最大问题，算法交替执行最小化和最大化步骤。固定任务参数 $\psi$ 时，最小化 $\mathcal{L}(\varphi ,\psi )$ 相当于执行标准的基于模型的强化学习（MBRL）。这意味着，我们在特定任务上调整模型参数 $\varphi$ 来提高性能。

2. 内部最大化问题：当模型 ${\hat{T}}_{\varphi }$ 被固定时，内部最大化任务参数 $\psi$ 是一项非平凡的任务。这涉及到寻找最难的任务，即使得模型表现和真实表现之间的差距最大的任务。这要求我们计算子最优性差距 $\mathcal{L}(\varphi ,\psi )$ 关于任务参数 $\psi$ 的梯度。

3. 梯度计算：梯度的计算涉及几个部分：

   • ${\theta }^{\ast }$ 是在真实动态下的最优策略参数。
   • $\hat{\theta }$ 是在虚拟（学习到的）动态下的最优策略参数。
   • $\frac{\partial {\eta }^{\ast }}{\partial \psi }$ 表示真实最优策略期望回报关于任务参数的梯度。
   • $\frac{\partial {\hat{\eta }}_{\varphi }}{\partial \psi }$ 表示在学习到的动态下最优策略期望回报关于任务参数的梯度。
   • $\frac{\partial \hat{T}}{\partial \theta }$ 表示学习到的动态模型关于策略参数的梯度。

   子最优性差距的梯度反映了当任务参数变化时，子最优性差距如何变化。通过对 $\psi$ 应用梯度上升，我们可以找到使模型与实际表现之间差异最大的任务设置。

4. 算法的目标：通过在这些最难的任务上训练，目标是使模型更准确地反映现实世界的动态，从而减少模型的不准确性并提高元强化学习算法的整体性能。

总之，这个过程涉及到找到使学习模型的表现与真实世界表现之间的差距最大化的任务参数，然后调整这些参数以改善模型的准确性和策略的性能。这种方法旨在通过针对性地解决模型在哪里最不准确的问题来提高模型的整体效能。

首先，对于期望回报 ${\eta }^{\ast }$ 相对于任务参数 $\psi$ 的导数，我们有：

$$\frac{\partial {\eta }^{\ast }}{\partial \psi }={\mathbb{E}}_{\tau \sim {\pi }_{{\theta }^{\ast }},T^{\ast }}\left[\sum _{t=0}^{\infty }{\gamma }^t\frac{\partial R_{\psi }(\tau )}{\partial \psi }\right]$$

这里表示的是，当你改变任务参数 $\psi$ 时，真实环境中最优策略产生的期望回报是如何变化的。这个期望值是通过所有可能轨迹的集合来计算的，其中每条轨迹都是根据最优策略 ${\pi }_{{\theta }^{\ast }}$ 和真实动态 $T^{\ast }$ 生成的。

接下来，考虑如何通过标准策略梯度方法来计算 $\frac{\partial {\eta }^{\ast }}{\partial \theta }$ 在 $\hat{\theta }$ 下的值，这里 $\hat{\theta }$ 是在学习到的动态 ${\hat{T}}_{\varphi }$ 下的最优策略参数：

$$\frac{\partial {\eta }^{\ast }}{\partial \theta }{|}_{\hat{\theta }}={\mathbb{E}}_{\tau \sim {\pi }_{\hat{\theta }},T^{\ast }}\left[\sum _{t=0}^{\infty }{\gamma }^t\frac{\partial \log {\pi }_{\hat{\theta }}(a_t|s_t)}{\partial \theta }{A}^{{\pi }_{\hat{\theta }}}(s_t,a_t)\right]$$

这个公式是策略梯度的标准形式，其中 $A^{{\pi }_{\hat{\theta }}}(s_t,a_t)$ 是优势函数，表示在状态 $s_t$ 下采取动作 $a_t$ 相对于平均策略的额外回报。

所以，当我们讨论公式(2)的梯度时，这实际上涉及到两个主要部分：

1. 真实环境下期望回报对任务参数 $\psi$ 的影响，这直接关联到奖励函数如何随 $\psi$ 变化。
2. 在学习到的动态下，期望回报如何随策略参数变化，这是通过策略梯度方法和优势函数来衡量的。

这些组合起来就形成了我们在调整任务参数 $\psi$ 时需要考虑的梯度部分，使得我们能够针对特定的任务参数调整来优化子最优性差距 $\mathcal{L}(\varphi ,\psi )$。

1. 首先，关于方程(2)中复杂部分的导数 $\frac{\partial \hat{T}}{\partial {\psi }^T}$，我们使用隐函数定理来计算。具体表达式为：

   $$\frac{\partial \hat{\theta }}{\partial {\psi }^T}=-{\left(\frac{{\partial }^2{\hat{\eta }}_{\varphi }}{\partial \theta \partial {\theta }^T}{|}_{\hat{\theta }}\right)}^{-1}\frac{{\partial }^2{\hat{\eta }}_{\varphi }}{\partial \theta \partial {\psi }^T}{|}_{\hat{\theta }}$$

   这是方程(5)的内容，表示通过隐函数定理如何求出策略参数对任务参数的导数。

2. 混合导数项，也就是策略梯度中涉及到的导数，可以通过以下方式计算：

   $$\frac{{\partial }^2{\hat{\eta }}_{\varphi }}{\partial \theta \partial {\psi }^T}={\mathbb{E}}_{\tau \sim {\pi }_{\hat{\theta }},{\hat{T}}_{\varphi }}\left[\sum _{t=0}^{\infty }{\gamma }^t\frac{\partial \log {\pi }_{\hat{\theta }}(a_t|s_t)}{\partial \theta }\frac{\partial A^{{\pi }_{\hat{\theta }}}(s_t,a_t)}{\partial {\psi }^T}\right]$$

   这是方程(6)的内容，涉及到策略参数和任务参数的混合导数。

3. 对于海森矩阵项（Hessian）的估计器，在方程(5)中提到，可以通过REINFORCE估计器得到：

   $$\frac{{\partial }^2{\hat{\eta }}_{\varphi }}{\partial \theta \partial {\theta }^T}={\mathbb{E}}_{\tau \sim {\pi }_{\hat{\theta }},{\hat{T}}_{\varphi }}\left[\left(\frac{\partial \log {\pi }_{\hat{\theta }}(\tau )}{\partial \theta }\frac{\partial \log {\pi }_{\hat{\theta }}(\tau )}{\partial {\theta }^T}+\frac{{\partial }^2\log {\pi }_{\hat{\theta }}(\tau )}{\partial \theta \partial {\theta }^T}\right)R_{\psi }(\tau )\right]$$

   这是方程(7)的内容，用于计算与策略参数相关的二阶导数，即海森矩阵。

通过使用隐函数定理，我们不需要对任务参数进行反向传播，这使得整个估计过程更加高效和可行。这些方程提供了一种方法，通过隐式地解决方程来更新策略参数，使得我们能够以样本高效和计算上可行的方式估计与任务参数相关的梯度。

这一章节涉及的梯度计算主要关注于元强化学习中如何针对特定任务参数优化策略。这里的物理意义或者更贴切地说，其在强化学习领域内的意义，涉及到如何根据任务的不同调整策略以达到最优表现。下面是每个部分的解释：

1. 梯度 $\frac{\partial {\eta }^{\ast }}{\partial \psi }$：这表示当你改变任务参数 $\psi$（比如，任务的目标或环境的状态），真实环境中最优策略导致的期望回报将如何变化。在强化学习中，这有助于我们理解，对于特定的任务变化，最优行为策略需要如何调整。

2. 梯度 $\frac{\partial {\eta }^{\ast }}{\partial \theta }{|}_{\hat{\theta }}$：这是标准策略梯度公式，表示在估计动态下，策略参数 $\theta$
   的微小变化如何影响策略的性能。通过这个梯度，我们可以优化策略，使其在给定的模拟环境下表现更好。

3. 混合导数项 $\frac{{\partial }^2{\hat{\eta }}_{\varphi }}{\partial \theta \partial {\psi }^T}$：这一项涉及到策略参数和任务参数之间的交互作用。它告诉我们，当任务参数发生变化时，我们如何调整策略参数以适应这些变化。这对于设计能够适应不同任务的通用策略非常重要。

4. Hessian 项 $\frac{{\partial }^2{\hat{\eta }}_{\varphi }}{\partial \theta \partial {\theta }^T}$ 的估计：这是通过REINFORCE估计器导出的，它涉及到策略的二阶导数，这有助于我们更精确地调整策略参数以适应环境的变化。

物理意义或直观理解是，通过这些导数和梯度的计算，我们能够在不同的任务之间转换策略，同时确保策略保持高效和适应性。这对于元强化学习特别重要，因为它的目标是开发能够快速适应新任务的策略。这些梯度帮助我们理解不同任务特征如何影响最优策略，并提供了一个系统的方式来自动调整策略以面对新的挑战。简而言之，这些计算帮助我们构建和优化那些能够理解和适应任务变化的智能策略。

4.3 AdMRL: a Practical Implementation

上述描述了元强化学习算法 AdMRL（Adversarial Meta-Reinforcement Learning）的过程。下面是对其流程的解释：

1. 算法概述：算法 AdMRL 通过交替更新动态模型 ${\hat{T}}_{\varphi }$ 和任务参数 $\psi$ 来适应不同的任务。`VirtualTraining($\theta ,\varphi ,\psi ,D,n$) 是一个学习动态模型 $\varphi$ 的过程，其中 $\theta$ 是策略参数，$\psi$ 是任务参数，$D$ 是数据集，而 $n$ 是虚拟步骤的数量。

2. 算法流程：

   • 首先，对于每个训练任务参数化为 $\psi$，初始化策略参数 $\theta$ 随机，并在学习到的动态 $\varphi$ 上优化策略直至收敛，这一步骤称为“零次适应”（zero-shot adaptation，见 Line 4）。
   • 接下来，使用得到的策略 ${\pi }_{\hat{\theta }}$ 从真实环境收集数据，并执行基于模型的强化学习算法 SLBO（见 Line 5），这涉及交替收集样本、更新模型和优化策略。
   • 收集样本和执行 SLBO 更新后，获得几乎最优的策略 ${\pi }_{{\theta }^{\ast }}$。

3. 梯度更新：

   • 使用策略 ${\pi }_{\hat{\theta }}$ 和 ${\pi }_{{\theta }^{\ast }}$，计算每个梯度分量（见 Line 9、10），并针对任务参数 $\psi$ 执行梯度上升（见 Line 12）。
   • 对于第一个训练任务，会跳过零次适应阶段并直接进行 SLBO 更新，因为此时动态模型尚未训练。

4. 外部迭代：完成外部迭代后，对于每个任务，算法都会更新任务参数 $\psi$，以便更好地适应该任务。

通过以上步骤，AdMRL 旨在快速适应新任务，利用从真实环境收集的数据不断优化动态模型和策略。这种方法结合了模型的优点，即能够预测环境动态，和策略的优点，即能够指导行为，以实现元学习的目标，即快速适应新的、未见过的任务。

上述描述的是如何在模型中计算特定于任务参数的梯度，并涉及到求解一个逆Hessian向量乘积问题。这在大规模问题中是常见的，因为直接计算和存储整个Hessian矩阵是非常昂贵的。

1. 逆Hessian向量乘积的计算：计算等式(5)的核心是求解方程 $Ax=b$，其中 $A=\frac{{\partial }^2{\hat{\eta }}_{\varphi }}{\partial \theta \partial {\theta }^T}{|}_{\hat{\theta }}$ 是Hessian矩阵，而 $b=\frac{{\partial }^2{\hat{\eta }}_{\varphi }}{\partial \theta \partial {\psi }^T}{|}_{\hat{\theta }}$。直观上，$A$ 是策略性能（如期望回报 ${\hat{\eta }}_{\varphi }$）关于策略参数 $\theta$ 的二阶导数，而 $b$ 描述策略性能如何随任务参数 $\psi$ 和策略参数 $\theta$ 的改变而改变。

2. 共轭梯度法的应用：在大规模问题中，由于存储和直接计算整个Hessian矩阵 $A$ 是不切实际的，所以使用共轭梯度法来近似求解 $Ax=b$。共轭梯度法是一种迭代方法，它不需要形成完整的Hessian矩阵 $A$，而是只需能计算任意向量 $x$ 与 $A$ 的乘积 $Ax$。这种方法显著降低了内存和计算需求。

3. Hessian向量乘积的效率问题：虽然共轭梯度法提供了一种计算上可行的解决方案，但在实践中发现，如果Hessian矩阵 $A$ 不是正定的（即不保证有唯一最小解），共轭梯度方法的收敛可能会受到影响。因此，改为求解等价问题 $A^{T}Ax=A^{T}b$，这个新问题具有更好的数学属性，有助于共轭梯度方法的收敛。

这个过程的物理意义在于，它提供了一种在复杂动态环境中有效更新策略参数的方法，尤其是在参数空间很大（如深度学习模型）时。通过近似逆Hessian向量乘积，可以在不牺牲过多精度的情况下，有效地估计如何调整策略参数以改善性能，这是许多先进强化学习和元学习方法的核心部分。通过这种方式，算法能够更好地适应新的任务，提高在不同环境中的表现。

上述讨论的是计算关于任务参数的梯度的时间复杂度，并将其与模型基础强化学习（MBRL）算法的其他步骤进行了比较。

首先，在每次任务迭代中，MBRL算法需要采集样本以适应动态模型，然后使用学习到的动态模型展开 $m$ 个虚拟样本来更新策略。这个过程的时间复杂度是 $O(m(d_{\varphi }+d_{\theta }))$，其中 $d_{\varphi }$ 是动态模型参数的维度，$d_{\theta }$ 是策略参数的维度。这表示每次迭代的计算成本随着虚拟样本数量的增加和参数的维度而增加。

另一方面，描述了关于任务参数 $\psi$ 的梯度计算相对来说更为高效。每次任务迭代中只需更新一次任务参数，这个过程的时间复杂度是 $O(d_{\psi }{d}_{\theta })$，其中 $d_{\psi }$ 是任务参数的维度。由于 $d_{\psi }$ 通常远小于 $d_{\varphi }$，且任务参数的维度较小（通常是一个小常数），因此这一步骤的时间复杂度相对较低。

在实践中，MBRL算法可能需要数百万个虚拟样本（$m$ 的值很大）来解决任务，但由于任务参数的维度 $d_{\psi }$ 较小，所以计算关于任务参数的梯度的时间成本可以忽略不计。

简而言之，这意味着在整个算法运行中，与模型动态和策略更新相关的计算负担要重得多，而更新任务参数的计算负担相对较轻。这使得元学习算法在面对高维动态模型和策略参数时，仍然可以有效地针对不同任务调整其策略。

上述讲述的是样本复杂性在元强化学习算法中的应用。虽然计算梯度估计器需要样本，但在实践中，我们可以重用MBRL算法收集和使用的样本来计算关于任务参数的梯度，这意味着在计算关于任务参数的梯度时，几乎不需要额外的样本。

具体来说，这表示当执行基于模型的强化学习（MBRL）算法时，你会收集一系列的样本来训练你的模型。然后，这些相同的样本可以被再次利用，以估计元学习任务中任务参数的梯度。这种方法的优点是它极大地减少了需要收集新样本的需求，从而降低了学习过程的样本复杂性。
因此，核心信息是，在计算任务参数梯度时，通过重用已有的MBRL样本，可以有效减少计算资源的需求，从而提高算法的样本效率。

上述讨论的是提出的方法与传统元强化学习（Meta-RL）之间的关系。它说明了该方法的假设、应用的现实意义、以及它在面对任务变化时的健壮性。

1. 方法的假设：这种方法假设了任务参数的知识，这与标准的Meta-RL设置有所不同。在传统的Meta-RL设置中，通常不假定对任务参数有先验知识。

2. 应用的现实意义：尽管这种方法假设了任务参数的知识，作者认为这一设置（a）在实践中是相关的，并且（b）为更高效和健壮的算法提供了新的机会。即，在现实世界应用中，手工设计的奖励函数家族是合理的，即使这不是常见的情况。

3. 面对任务变化时的健壮性：如果我们甚至不知道测试任务的家族，那么在测试时做出准确的调整是具有挑战性的，如果不是不可能的话。然而，该方法通过限制设置使其能够对最坏情况下的任务变化保持健壮。

4. 未来的工作方向：在训练时已知任务家族但在测试时任务参数未知的情况下，可能存在一些中间形式的方法。这意味着未来的工作可能会探索在训练时识别任务家族，然后在测试时推断任务参数的方法。

5 Experiments

上述概述了实验的目的和关键问题，以及实验的设置：

1. AdMRL的性能评估：实验旨在评估AdMRL（对抗性元强化学习）在标准元强化学习基准上与现有最先进方法相比的表现。

2. 最坏情况性能：探究AdMRL是否能够在分布式元强化学习方法中实现更好的最坏情况性能。

3. 高维任务参数环境中的性能：研究AdMRL在任务参数是高维时的表现。

4. 泛化能力：评估AdMRL在分布外任务（即在训练过程中未见过的任务）上的泛化能力。

实验采用基于OpenAI Gym的连续控制任务进行评估，并使用MuJoCo物理模拟器进行环境模拟。这意味着实验旨在评价AdMRL算法在处理复杂、连续动作空间的任务中的有效性和鲁棒性。

上述描述的是低维度速度控制任务的设置。这些任务是基于控制二维（2-D）或三维（3-D）速度的环境和任务。文中讨论了三种受欢迎的MuJoCo环境：Hopper、Walker和Ant，并且为这些环境定义了任务参数$\psi =({\psi }_x,{\psi }_y,{\psi }_z)$，这些参数分别对应于目标的$x$速度、$y$速度和$z$位置。

对于任务参数，代理的目标是使其$x$和$y$方向的速度以及$z$方向的位置尽可能匹配目标参数。奖励函数定义为：

$$r_{\psi }(v_x,v_y,z)=c_1|v_x-{\psi }_x|+c_2|v_y-{\psi }_y|+c_3|h_z-{\psi }_z|$$

其中，$v_x$和$v_y$表示$x$和$y$方向的速度，$h_z$表示$z$方向的高度（位置），$c_1$、$c_2$、$c_3$是手动设定的系数，确保奖励的每个组成部分都能相似地贡献。

任务参数集$\psi$是一个三维空间的盒子（对于3-D任务），可以根据特定环境而变化。例如，Ant3D的任务参数集合$\Psi$定义为$\Psi =[-3,3]\times [-3,3]\times [0.4,0.6]$，这里$z$位置的范围是选定的，以便目标大多数情况下是可实现的。

对于2-D任务，设置类似，但只涉及两个这样的值，即$x$和$y$方向的速度，而$z$方向被固定或不考虑。在实践中，当任务参数具有更多自由度时，任务分布的变化将变得更为显著，因此作者扩展了2-D设置到3-D，以突出任务分布变化时的挑战。

高维度任务:

• 我们还创建了一组更复杂的高维度任务，以测试我们的算法在处理具有更多自由度的对抗性任务中的表现。这里，奖励函数是线性的，基于状态的后转移状态$s^{\prime }$，即$r_{\psi }(s,a,s^{\prime })={\psi }^T{s}^{\prime }$，其中$\psi \in {\mathbb{R}}^d$（$d$是状态维度）。
• 任务参数$\psi$的集合是$\Psi =[-1,1{]}^d$。这意味着代理的目标是采取行动使$s^{\prime }$最直接地与某个目标向量$\psi$线性相关。
• 在这里，我们使用了HalfCheetah环境，其中$d=18$。为了确保每个状态坐标对总奖励有类似的贡献，我们通过状态$s$减去平均值$\mu$并除以标准差$\sigma$来规范化状态，这里的$\mu$和$\sigma$是从所有收集的真实环境状态中计算出来的。

1. 训练过程：

   • AdMRL算法的训练过程是基于先前的元强化学习方法，特别是MAML（模型无关的元学习）和PEARL（概率嵌入适应性强化学习）。AdMRL根据SLBO（随机下界优化）算法的代码构建，这是一种模型基础的强化学习方法。

2. 样本效率：

   • 在训练过程中，AdMRL相对于MAML和PEARL展示了更高的样本效率。MAML和PEARL分别需要80和2.5百万样本，而AdMRL仅需要0.4或0.8百万样本。

3. 任务参数：

   • 不同于标准的元强化学习方法，AdMRL还利用了任务参数（$\psi$）来明确影响训练过程。这意味着AdMRL不仅学习一般的策略，而且还能根据具体任务调整其策略。

4. 实验设置：

   • AdMRL在不同数量的训练任务上进行实验，从10个任务到20个任务。这与允许MAML和PEARL在更广泛的任务上进行训练以保持公平比较是不同的。

5. 多任务策略：

   • 除了传统的元强化学习方法外，AdMRL还与几种基于多任务策略的方法进行了比较，这些方法直接利用任务参数。比较包括：
     • (A) MT-joint：联合训练多任务策略 $\pi (a|s,\psi )$。
     • (B) MAML-MT和PEARL-MT：这两种方法通过多任务策略替换了MAML和PEARL中的策略。

通过以上解释，我们可以理解AdMRL如何提供一种在样本效率和任务适应性方面都优于传统元强化学习方法的新策略。这在处理广泛且多变的任务时尤其重要，尤其是当这些任务具有不同的环境参数和目标时。

这一段描述的是一种用于评估低维和高维速度控制任务的评价指标。在低维任务中，如Hopper2D、Walker2D和Ant2D，任务在一个6×6×6的网格中被枚举。对于三维任务如Ant3D，会在边界上随机采样20个测试任务。对于每个任务$\psi$，比较不同算法在以下三个方面的性能：$A_0(\psi )$（零样本适应性能），$A_n(\psi )$（收集n个样本后的适应性能），以及$G_n(\psi )=A^{\ast }(\psi )-A_n(\psi )$（最坏情况下的次优性能差距）。实验中，AdMRL与MAML和PEARL在所有环境中进行了比较，样本数量为2000、4000、6000。同时，AdMRL还与在最坏情况下任务中使用均匀或高斯任务采样分布的分布式变体进行了比较，用于处理高维任务和分布外（OOD）任务。

5.1 Adaptation Performance Compared to Baselines

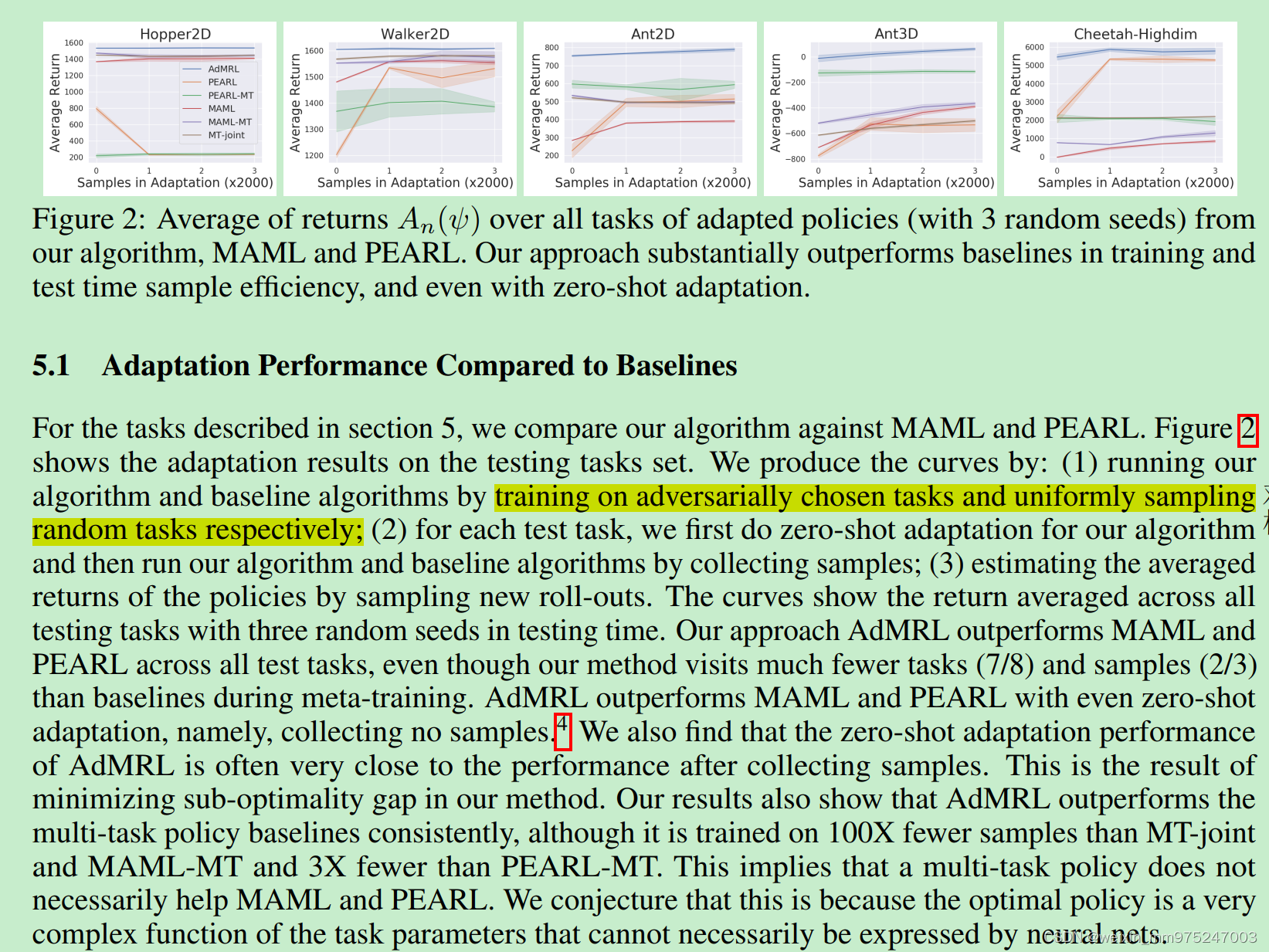
1. 训练和测试任务的准备：AdMRL算法以及基线算法（比如MAML和PEARL）在两种不同的任务集上进行训练：一种是“对抗性选择的任务”（adversarially chosen tasks），另一种是“均匀采样的随机任务”（uniformly sampling random tasks）。这意味着AdMRL不仅在预先定义好的任务上进行测试，还在通过某种策略特别选择的更具挑战性的任务上进行测试。

2. 零样本适应性测试：在每个测试任务上，首先进行零样本适应（zero-shot adaptation），即不收集任何新样本，直接使用已经学习的知识进行任务。然后收集样本并运行算法及基线算法，以便比较它们在收集新信息后的表现。

3. 性能评估：使用三种不同的指标来评估任务性能：$A_0(\psi )$（零样本适应性能），$A_n(\psi )$（收集n个样本后的适应性能），和$G_n(\psi )$（最坏情况下的次优性能差距）。这些指标帮助比较在不同采样条件下算法的适应能力和鲁棒性。

4. 结果分析：AdMRL在所有测试任务上表现优于MAML和PEARL，即使在不收集任何新样本的情况下也是如此。这表明AdMRL在元训练期间学到的策略更具通用性和适应性。此外，AdMRL在训练时需要的样本数量远少于MAML和PEARL，这意味着它更高效。

5. 结论：尽管AdMRL训练时使用的样本少得多，但它在多任务策略上表现出更好的适应性，这意味着一个任务的多样性对于元学习算法来说是一个重要因素。而且，这也暗示了多任务策略在表达复杂任务参数时可能并不总是优于特定的、针对性的策略。

5.2 Comparing with Model-based Baselines in Worst-case Sub-optimality Gap

上述讨论了AdMRL算法与基于模型的基线方法（MB-Unif和MB-Gauss）在最坏情况下次优性能差距（sub-optimality gap）的比较。我们来一步步解释：

1. 次优性能差距（Sub-optimality Gap）$G_n(\psi )$：这是衡量算法在特定任务$\psi$上与最佳可能性能之间的差距。$G_n(\psi )$是对于给定任务$\psi$，经过$n$次样本适应后的策略与最优策略之间性能的差异。数值越低表示算法表现越接近最优。

2. AdMRL与MB-Unif和MB-Gauss的比较：这里比较的是AdMRL、MB-Unif（基于均匀分布的任务采样的模型基方法）和MB-Gauss（基于高斯分布的任务采样的模型基方法）的性能。图3(a)展示了不同任务参数$\psi$下的$G_n(\psi )$值，图像中的颜色越浅表示次优性能差距越小，即算法表现越好。

3. 实验结果的解释：

   • 图3(a)：显示了AdMRL在各个测试任务上的次优性能差距相对于MB-Unif和MB-Gauss是较小的，尤其是在任务参数空间的边界上，这表示AdMRL在最坏情况下具有更好的泛化能力。
   • 图3(b)：展示了随着适应样本数量增加，AdMRL在Ant2D环境中的次优性能差距如何变化，并与MB-Unif和MB-Gauss进行比较。图中AdMRL的曲线显示出更低的次优性能差距，意味着其适应性更好。

4. 总结：这一部分的研究表明，AdMRL算法在对抗性选择的任务中，特别是在任务参数空间的边界上，相比于基于特定分布采样任务的模型基方法，能够实现更小的次优性能差距，说明了其在面对未知或变化大的任务时具有更好的适应性和泛化能力。
   AdMRL算法在处理高维任务上的性能，尤其是与基于模型的基线方法MB-Unif和MB-Gauss相比较的情况。我们来逐句解释：

5. 高维任务性能（Performance on high-dimensional tasks）：在高维任务参数条件下，AdMRL算法的表现显著优于MB-Unif和MB-Gauss。这里的“高维”意味着任务的参数非常多，给任务设计和算法优化带来了更大的挑战。

6. 次优性能差距（Sub-optimality Gap）：AdMRL在适应过程中的次优性能差距较小。这个差距是指算法当前表现与理论上最佳可能表现之间的差异。较小的差距意味着算法的表现更接近最优。

7. 高维任务的多样性：在高维任务中，每个任务都有不同的最优行为模式。这增加了问题的复杂性，因为算法必须能够适应一系列不同的最优解。

8. 对比随机采样方法：传统的基于分布的方法（如MB-Unif和MB-Gauss），通过从某个给定的任务分布中随机采样来进行元训练，这种方法在高维任务中往往效率较低，因为很难通过随机采样覆盖到所有具有最大次优性能差距的任务。

9. 非分布式对抗选择方法：AdMRL采用的是一种非分布式对抗选择方式，这意味着它不是简单地从任务分布中随机选择任务进行训练，而是更加高效地寻找那些最难的任务，并在这些任务上训练模型以最小化最坏情况下的次优性能差距。
   
   上述字主要说明了AdMRL（自适应对抗元强化学习）算法如何在Ant3D环境中的元训练期间选择任务的参数ψ，并与基于模型的统一方法（MB-Unif）和基于高斯分布的方法（MB-Gauss）进行比较。

10. 任务的选择（任务参数ψ的可视化）：AdMRL能够快速地定位到有大次优性能差距的任务，尤其是在参数空间的边界上。这意味着AdMRL不是随机选择任务进行训练，而是能够识别并优先训练那些最具挑战性（即“难”任务）的任务，这些任务对模型训练最为信息丰富。

11. 与传统方法的比较：相对于MB-Unif和MB-Gauss，这两种方法通过从均匀分布或高斯分布中随机采样任务参数来选择任务，AdMRL的方法更可能选择边界上的任务，而这些任务通常更难，但为模型提供了更重要的学习信息。

12. 任务空间的探索：图中的三维图示显示了各种方法在任务参数空间中探索的范围。MB-Unif和MB-Gauss主要在中心区域集中，而AdMRL探索了更广泛的空间，包括边界区域，这表明AdMRL在探索任务空间时更加全面和有效。

13. 次优性能差距（Sub-optimality Gap）：图中还比较了这些方法在适应新任务时的性能，特别是在高维任务中AdMRL如何实现最小的最坏情况次优性能差距$G_{\text{max}}^n(\psi )$，这表示AdMRL在适应新任务时比其他方法更接近最优解。

5.3 Out-of-distribution Performance

上述展示了AdMRL算法在Ant2D环境中对于分布外（OOD, Out-Of-Distribution）任务的表现，并与两种基于模型的基线方法MB-Unif和MB-Gauss进行了比较。图5(a)展示了不同任务参数ψ下，这三种方法适应策略后的次优性能差距$G_n(\psi )$，这里n = 6K表示在适应过程中使用的样本数量。次优性能差距是指策略从最优性能差距多远，数值越小表示性能越接近最优。

• 次优性能差距（Sub-optimality Gap）：在图5(a)中，不同的颜色深度表示不同的次优性能差距大小，颜色越浅表示差距越小，即策略表现越好。可以看出，AdMRL在多数任务参数设置下，都比MB-Unif和MB-Gauss表现得更好，尤其是在任务参数空间的边界处，这表明AdMRL具有更好的泛化能力。

• 泛化能力：AdMRL在面对OOD任务时显示出比MB-Unif和MB-Gauss更低的次优性能差距，这意味着AdMRL能更好地适应新颖或未见过的任务。

• 图5(b)的曲线：展示了随着适应过程中样本数量增加，不同方法的次优性能差距的变化。可以看到，随着样本数的增加，AdMRL的次优性能差距通常比MB-Unif和MB-Gauss更低，这再次证明了其较好的学习和泛化能力。
  
  上述展示了在Ant2D环境中，基于不同方法（AdMRL、MB-Unif、MB-Gauss）学习得到的模型的预测误差。这里使用的是L2损失来衡量模型的预测误差，L2损失越小，表示模型的预测越准确。

从图中可以看出，由AdMRL学习得到的模型的L2损失最小，意味着其预测精度高于MB-Unif和MB-Gauss学习的模型。换言之，AdMRL方法在处理超出分布（OOD）任务时，能够更准确地捕捉到真实动态的特性，从而产生更准确的预测。

说明了AdMRL在模型学习质量方面相对于MB-Unif和MB-Gauss的优越性。这表示AdMRL不仅在最优性能上表现更好，而且在模型预测的准确性上也更胜一筹。

作者提出了一种新的方法，称为基于模型的对抗性元强化学习（AdMRL），旨在解决元强化学习（meta-RL）中的分布偏移问题。作者定义了对抗性元-RL问题，并提出了一种最小最大（minimax）公式，以最小化最坏情况下的次优性能差距。为了高效优化，他们导出了关于任务参数的梯度的估计器，并利用共轭梯度法实现了该估计器的高效使用。他们在标准基准环境上提供了广泛的实验结果，展示了他们的方法相对于先前的元-RL算法的有效性。

对于未来的研究方向，他们提出了几个有趣的点：

1. 将AdMRL应用到更困难的设置中，例如视觉领域。
2. 用其他基于模型的强化学习（MBRL）算法替换SLBO。
3. 将AdMRL应用于奖励函数的参数化未知的情况。

AdMRL提出了一种新颖的方法来解决元强化学习中的关键问题，并展示了其在多种设置中的应用潜力。此外，他们还计划将这种方法扩展到更多的应用和更复杂的场景中。