- 1[uni-app] canvas绘制圆环进度条_uniapp 环形进度条
- 2Linux网络子系统中报文的接收及NAPI的实现_netif_napi_add
- 3python怎么求因子之和_P066 求n的所有因子之和 ★★
- 4H5如何调用小程序分享 微信SDK_微信sdk支持h5直接唤起分享吗
- 5nmap在kali的使用方法和常见命令(入门)_kali的nmap用法
- 6leetcode 矩阵置零 java_leetcode java 矩阵置零
- 7封装请求拦截器、响应拦截器原理
- 8在 Linux 中,文件总共被分成了 7 种_linux中7种主要文件类型
- 9gcc g++环境变量设置_MinGW + 配置系统环境变量
- 10带有反斜杠的字符串如何转json对象_vue json 里面有反斜杠的怎么转成json
分布式&数据结构与算法面试题_分布式更多的一个概念,是为了解决单个物理服务器容量和性能瓶颈问题而采用的优化
赞
踩
分布式
分布式概述
分布式
分布式(distributed)是为了解决单个物理服务器容量和性能瓶颈问题而采用的优化手段,将一个业务拆分成不同的子业务,分布在不同的机器上执行。服务之间通过远程调用协同工作,对外提供服务。
该领域需要解决的问题极多,在不同的技术层面上,又包括:分布式缓存、分布式数据库、分布式计算、分布式文件系统等,一些技术如MQ、Redis、zookeeper等都跟分布式有关。
从理念上讲,分布式的实现有两种形式:
水平扩展:当一台机器扛不住流量时,就通过添加机器的方式,将流量平分到所有服务器上,所有机器都可以提供相同的服务;
垂直拆分:前端有不同业务需求时,一台机器扛不住流量,可以将不同的业务需求分发到不同的机器上,比如A机器处理余票查询的请求,B机器处理支付的请求。
集群
集群(cluster)是指在多台不同的服务器中部署相同应用或服务模块,构成一个集群,通过负载均衡设备对外提供服务。
两个特点
可扩展性:集群中的服务节点,可以动态的添加机器,从而增加集群的处理能力。
高可用性:如果集群某个节点发生故障,这台节点运行的服务,可以被其他服务节点接管,从而增强集群的高可用性。
两大能力
负载均衡:负载均衡能把任务比较均衡地分布到集群环境下的服务节点上。
集群容错:集群服务调用失败后,服务框架能够根据容错策略在底层自动容错,不影响服务的正常提供
微服务
微服务就是很小的服务,小到一个服务只对应一个单一的功能,只做一件事。这个服务可以单独部署运行,服务之间通过远程调用协同工作,每个微服务都是由独立的小团队开发,测试,部署,上线,负责它的整个生命周期。
多线程
多线程(multi-thread):多线程是指程序中包含多个执行流,即在一个程序中可以同时运行多个不同的线程来执行不同的任务。多线程是为了提高CPU的利用率。
高并发
高并发(High Concurrency)是一种系统运行过程中发生了一种“短时间内遇到大量请求”的情况,高并发对应的是访问请求,多线程是解决高并发的方法之一,高并发还可以通过分布式,集群,算法优化,数据库优化等方法解决。
分布式系统设计理念
分布式系统的目标与要素
分布式系统的目标是提升系统的整体性能和吞吐量,另外还要尽量保证分布式系统的容错性(假如增加10台服务器才达到单机运行效果2倍左右的性能,那么这个分布式系统就根本没有存在的意义)。
即使采用了分布式系统,我们也要尽力运用并发编程、高性能网络框架等等手段提升单机上的程序性能。
分布式系统设计两大思路:中心化和去中心化
![]()
中心化设计
-
两个角色: 中心化的设计思想很简单,分布式集群中的节点机器按照角色分工,大体上分为两种角色:“领导” 和 “干活的”
-
角色职责: “领导”通常负责分发任务并监督“干活的”,发现谁太闲了,就想方设法地给其安排新任务,确保没有一个“干活的”能够偷懒,如果“领导”发现某个“干活的”因为劳累过度而病倒了,则是不会考虑先尝试“医治”他,而是一脚踢出去,然后把他的任务分给其他人。其中微服务架构 Kubernetes 就恰好采用了这一设计思路。
-
中心化设计的问题
-
中心化的设计存在的最大问题是“领导”的安危问题,如果“领导”出了问题,则群龙无首,整个集群就奔溃了。但我们难以同时安排两个“领导”以避免单点问题。
-
中心化设计还存在另外一个潜在的问题,既“领导”的能力问题:可以领导10个人高效工作并不意味着可以领导100个人高效工作,所以如果系统设计和实现得不好,问题就会卡在“领导”身上。
-
-
领导安危问题的解决办法: 大多数中心化系统都采用了主备两个“领导”的设计方案,可以是热备或者冷备,也可以是自动切换或者手动切换,而且越来越多的新系统都开始具备自动选举切换“领导”的能力,以提升系统的可用性。
去中心化设计
-
众生地位平等: 在去中心化的设计里,通常没有“领导”和“干活的”这两种角色的区分,大家的角色都是一样的,地位是平等的,全球互联网就是一个典型的去中心化的分布式系统,联网的任意节点设备宕机,都只会影响很小范围的功能。
-
“去中心化”不是不要中心,而是由节点自由选择中心。 (集群的成员会自发的举行“会议”选举新的“领导”主持工作。最典型的案例就是ZooKeeper及Go语言实现的Etcd)
-
去中心化设计的问题: 去中心化设计里最难解决的一个问题是 “脑裂”问题 ,这种情况的发生概率很低,但影响很大。脑裂指一个集群由于网络的故障,被分为至少两个彼此无法通信的单独集群,此时如果两个集群都各自工作,则可能会产生严重的数据冲突和错误。一般的设计思路是,当集群判断发生了脑裂问题时,规模较小的集群就“自杀”或者拒绝服务。
分布式事务
什么是分布式事务
分布式事务就是指事务的资源分别位于分布式系统的不同节点之上的事务
分布式事务产生的原因
数据库分库分表
当业务数据量达到单库单表的极限时,就需要考虑分库分表,跨多个数据库的事务操作就需要使用分布式事务
业务服务化
随着互联网快速发展,微服务,SOA等服务架构模式正在被大规模的使用,现在分布式系统一般由多个独立的微服务组成,多个微服务通过远程调用协同工作。跨系统的事务也属于分布式事务。
@$CAP定理
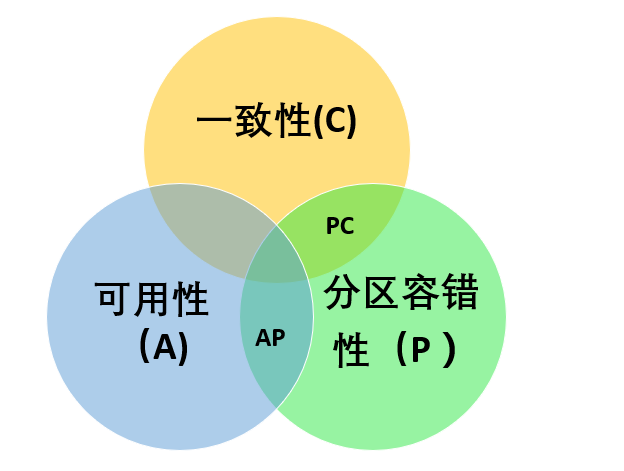
在理论计算机科学中,CAP定理(CAP theorem),又被称作布鲁尔定理(Brewer's theorem),它指出对于一个分布式计算系统来说,不可能同时满足以下三点:
| 选项 | 描述 |
|---|---|
| Consistency(一致性) | 指数据在多个副本之间能够保持一致的特性(对某个指定的客户端来说,读操作保证能够返回最新的写操作结果。这里并不是强调同一时刻拥有相同的数据) |
| Availability(可用性) | 指系统提供的服务必须一直处于可用的状态,每次请求都能获取到非错的响应(非故障的节点在合理的时间内返回合理的响应(不是错误和超时的响应)。不保证获取的数据为最新数据) |
| Partition tolerance(分区容错性) | 分布式系统在遇到任何网络分区故障的时候,仍然能够对外提供满足一致性和可用性的服务,除非整个网络环境都发生了故障 |
Spring Cloud在CAP法则上主要满足的是A和P法则,Dubbo和Zookeeper在CAP法则主要满足的是C和P法则
注意:不是所谓的3选2(不要被网上大多数文章误导了)
现实生活中,大部分人解释这一定律时,常常简单的表述为:“一致性、可用性、分区容错性三者你只能同时达到其中两个,不可能同时达到三者”。实际上这是一个非常具有误导性质的说法,而且在CAP理论诞生12年之后,CAP之父也在2012年重写了之前的论文。
当发生网络分区的时候,如果我们要继续服务,那么强一致性和可用性只能2选1。也就是说当网络分区之后P是前提,决定了P之后才有C和A的选择。也就是说分区容错性(Partition tolerance)我们是必须要实现的
值得补充的是,CAP理论告诉我们分布式系统只能选择AP或者CP,但实际上并不是说整个系统只能选择AP或者CP,在 CAP 理论落地实践时,我们需要将系统内的数据按照不同的应用场景和要求进行分类,每类数据选择不同的策略(CP 还是 AP),而不是直接限定整个系统所有数据都是同一策略。
CAP定理的证明
关于CAP这三个特性我们就介绍完了,接下来我们试着证明一下为什么CAP不能同时满足。
![]()
为了简化证明的过程,我们假设整个集群里只有两个N1和N2两个节点,如下图:
N1和N2当中各自有一个应用程序AB和数据库,当系统满足一致性的时候,我们认为N1和N2数据库中的数据保持一致。在满足可用性的时候,我们认为无论用户访问N1还是N2,都可以获得正确的结果,在满足分区容错性的时候,我们认为无论N1还是N2宕机或者是两者的通信中断,都不影响系统的运行。
我们假设一种极端情况,假设某个时刻N1和N2之间的网络通信突然中断了。如果系统满足分区容错性,那么显然可以支持这种异常。问题是在此前提下,一致性和可用性是否可以做到不受影响呢?
我们做个假设实验,如下图,突然某一时刻N1和N2之间的关联断开:
有用户向N1发送了请求更改了数据,将数据库从V0更新成了V1。由于网络断开,所以N2数据库依然是V0,如果这个时候有一个请求发给了N2,但是N2并没有办法可以直接给出最新的结果V1,这个时候该怎么办呢?
这个时候无非两种方法,一种是将错就错,将错误的V0数据返回给用户。第二种是阻塞等待,等待网络通信恢复,N2中的数据更新之后再返回给用户。显然前者牺牲了一致性,后者牺牲了可用性。
这个例子虽然简单,但是说明的内容却很重要。在分布式系统当中,CAP三个特性我们是无法同时满足的,必然要舍弃一个。
@$BASE理论
BASE理论由eBay架构师Dan Pritchett提出,在2008年上被分表为论文,并且eBay给出了他们在实践中总结的基于BASE理论的一套新的分布式事务解决方案。
BASE 是 Basically Available(基本可用) 、Soft-state(软状态) 和 Eventually Consistent(最终一致性) 三个短语的缩写。BASE理论是对CAP中一致性和可用性权衡的结果,其来源于对大规模互联网系统分布式实践的总结,是基于CAP定理逐步演化而来的,它大大降低了我们对系统的要求。
BASE理论的核心思想
即使无法做到强一致性,但每个应用都可以根据自身业务特点,采用适当的方式来使系统达到最终一致性。也就是牺牲数据的一致性来满足系统的高可用性,系统中一部分数据不可用或者不一致时,仍需要保持系统整体“基本可用”。
针对数据库领域,BASE思想的主要实现是对业务数据进行拆分,让不同的数据分布在不同的机器上,以提升系统的可用性,当前主要有以下两种做法:
-
按功能划分数据库
-
分片(如开源的Mycat、Amoeba等)。
BASE理论三要素
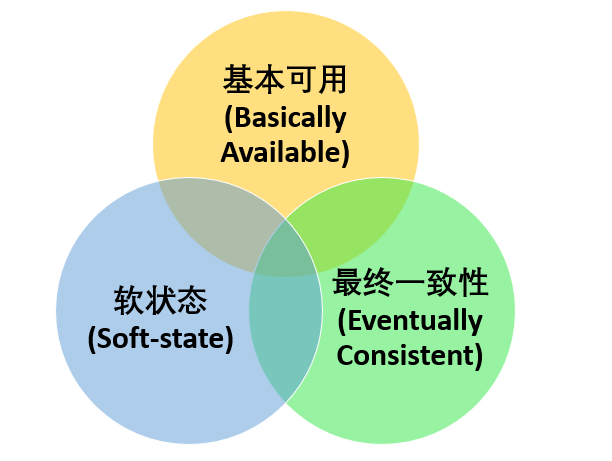
1. 基本可用
基本可用是指分布式系统在出现不可预知故障的时候,允许损失部分可用性。即保证核心可用。但是,这绝不等价于系统不可用。
比如:
-
响应时间上的损失:正常情况下,一个在线搜索引擎需要在0.5秒之内返回给用户相应的查询结果,但由于出现故障,查询结果的响应时间增加了1~2秒
-
系统功能上的损失:正常情况下,在一个电子商务网站上进行购物的时候,消费者几乎能够顺利完成每一笔订单,但是在一些节日大促购物高峰的时候,由于消费者的购物行为激增,为了保护购物系统的稳定性,部分消费者可能会被引导到一个降级页面
2. 软状态
软状态指允许系统中的数据存在中间状态,并认为该中间状态的存在不会影响系统的整体可用性,即允许系统在不同节点的数据副本之间进行数据同步的过程存在延时。这里的中间状态就是 CAP 理论中的数据不一致。
3. 最终一致性
最终一致性强调的是系统中的所有数据副本经过一定时间后,最终能够达到一致的状态。因此,最终一致性的本质是需要系统保证最终数据能够达到一致,而不需要实时保证系统数据的强一致性。
BASE 理论本质上是对 CAP 的延伸和补充,更具体地说,是对 CAP 中 AP 方案的一个补充:
-
CAP 理论是忽略延时的,而实际应用中延时是无法避免的。这一点就意味着完美的 CP 场景是不存在的,即使是几毫秒的数据复制延迟,在这几毫秒时间间隔内,系统是不符合 CP 要求的。因此 CAP 中的 CP 方案,实际上也是实现了最终一致性,只是“一定时间”是指几毫秒而已。
-
AP 方案中牺牲一致性只是指发生分区故障期间,而不是永远放弃一致性。这一点其实就是 BASE 理论延伸的地方,分区故障期间牺牲一致性,但分区故障恢复后,系统应该达到最终一致性。
数据一致性模型
分布式系统通过复制数据来提高系统的可靠性和容错性,并且将数据的不同的副本存放在不同的机器上,由于维护数据副本的一致性代价很高,因此许多系统采用弱一致性来提高性能,下面介绍常见的一致性模型:
-
强一致性 要求无论更新操作是在哪个数据副本上执行,之后所有的读操作都要能获得最新的数据。对于单副本数据来说,读写操作是在同一数据上执行的,容易保证强一致性。对多副本数据来说,则需要使用分布式事务协议。
-
弱一致性 在这种一致性下,用户读到某一操作对系统特定数据的更新需要一段时间,我们将这段时间称为"不一致性窗口"。
-
最终一致性 是弱一致性的一种特例,在这种一致性下系统保证用户最终能够读取到某操作对系统特定数据的更新(读取操作之前没有该数据的其他更新操作)。"不一致性窗口"的大小依赖于交互延迟、系统的负载,以及数据的副本数等。
系统选择哪种一致性模型取决于应用对一致性的需求,所选取的一致性模型还会影响到系统如何处理用户的请求以及对副本维护技术的选择等。
酸碱平衡
ACID能够保证事务的强一致性,即数据是实时一致的。这在本地事务中是没有问题的,在分布式事务中,强一致性会极大影响分布式系统的性能,因此分布式系统中遵循BASE理论即可。
但分布式系统的不同业务场景对一致性的要求也不同。如交易场景下,就要求强一致性,此时就需要遵循ACID理论,而在注册成功后发送短信验证码等场景下,并不需要实时一致,因此遵循BASE理论即可。因此要根据具体业务场景,在ACID和BASE之间寻求平衡。
柔性事务
柔性事务的概念
在电商等互联网场景下,传统的事务在数据库性能和处理能力上都暴露出了瓶颈。在分布式领域基于CAP理论以及BASE理论,有人就提出了柔性事务的概念。
基于BASE理论的设计思想,柔性事务下,在不影响系统整体可用性的情况下(Basically Available 基本可用),允许系统存在数据不一致的中间状态(Soft State 软状态),在经过数据同步的延时之后,最终数据能够达到一致(Eventually Consistent 最终一致性)。并不是完全放弃了ACID,而是通过放宽一致性要求,借助本地事务来实现最终一致性的同时也保证系统的吞吐。
实现柔性事务的一些特性
下面介绍的是实现柔性事务的一些常见特性,这些特性在具体的方案中不一定都要满足,因为不同的方案要求不一样。
可见性(对外可查询) 在分布式事务执行过程中,如果某一个步骤执行出错,就需要明确的知道其他几个操作的处理情况,这就需要其他的服务都能够提供查询接口,保证可以通过查询来判断操作的处理情况。
为了保证操作的可查询,需要对于每一个服务的每一次调用都有一个全局唯一的标识,可以是业务单据号(如订单号)、也可以是系统分配的操作流水号(如支付记录流水号)。除此之外,操作的时间信息也要有完整的记录。
操作幂等性 同一个方法,使用同样的参数,调用多次产生的业务结果与调用一次产生的业务结果相同。
之所以需要操作幂等性,是因为为了保证数据的最终一致性,很多事务协议都会有很多重试的操作,如果一个方法不保证幂等,那么将无法被重试。幂等操作的实现方式有多种,如在系统中缓存所有的请求与处理结果、检测到重复操作后,直接返回上一次的处理结果等。
@$常见分布式事务解决方案
介绍完分布式系统的一致性相关理论,下面基于不同的一致性模型介绍分布式事务的常见解决方案,后面会再介绍各个方案的使用场景。
分布式事务的实现有许多种,其中较经典是由Tuxedo提出的XA分布式事务协议,XA协议包含二阶段提交(2PC)和三阶段提交(3PC)两种实现。
常用概念
-
本地事务:由资源管理器本地管理的事务。本地事务的优点就是支持严格的ACID特性,高效,可靠,状态可以只在资源管理器中维护,而且应用编程模型简单。但是本地事务不具备分布式事务的处理能力,隔离的最小单位受限于资源管理器。
-
全局事务:当事务由全局事务管理器进行全局管理时称为全局事务,事务管理器负责管理全局的事务状态和参与的资源,协同资源的一致提交回滚。
-
TX协议:应用或者应用服务器与事务管理器的接口。
-
XA协议:全局事务管理器与资源管理器的接口。XA是由X/Open组织提出的分布式事务规范。该规范主要定义了全局事务管理器和局部资源管理器之间的接口。主流的数据库产品都实现了XA接口。XA接口是一个双向的系统接口,在事务管理器以及多个资源管理器之间作为通信桥梁。之所以需要XA是因为在分布式系统中从理论上讲两台机器是无法达到一致性状态的,因此引入一个单点进行协调。由全局事务管理器管理和协调的事务可以跨越多个资源和进程。全局事务管理器一般使用XA二阶段协议与数据库进行交互。
-
AP:应用程序。
-
RM:资源管理器,这里可以是一个DBMS或者消息服务器管理系统,应用程序通过资源管理器对资源进行控制,资源必须实现XA定义的接口。资源管理器负责控制和管理实际的资源。
-
TM:事务管理器,负责协调和管理事务,提供给AP编程接口以及管理资源管理器。事务管理器控制着全局事务,管理事务的生命周期,并且协调资源。
2PC(二阶段提交)方案 —— 强一致性
方案简介
二阶段提交协议(Two-phase Commit,即2PC)是常用的分布式事务解决方案,即将事务的提交过程分为两个阶段来进行处理:准备阶段和提交阶段。事务的发起者称协调者,事务的执行者称参与者。
在分布式系统里,每个节点都可以知晓自己操作的成功或者失败,却无法知道其他节点操作的成功或失败。当一个事务跨多个节点时,为了保持事务的原子性与一致性,而引入一个协调者来统一掌控所有参与者的操作结果,并指示它们是否要把操作结果进行真正的提交或者回滚(rollback)。
二阶段提交的算法思路可以概括为:参与者将操作成败通知协调者,再由协调者根据所有参与者的反馈情报决定各参与者是否要提交操作还是中止操作。
核心思想就是对每一个事务都采用先尝试后提交的处理方式,处理后所有的读操作都要能获得最新的数据,因此也可以将二阶段提交看作是一个强一致性算法。
处理流程
简单一点理解,可以把协调者节点比喻为带头大哥,参与者理解比喻为跟班小弟,带头大哥统一协调跟班小弟的任务执行。
阶段1:准备阶段
1、协调者向所有参与者发送事务内容,询问是否可以提交事务,并等待所有参与者答复。
2、各参与者执行事务操作,将undo和redo信息记入事务日志中(但不提交事务)。
3、如参与者执行成功,给协调者反馈yes,即可以提交;如执行失败,给协调者反馈no,即不可提交。
阶段2:提交阶段 如果协调者收到了参与者的失败消息或者超时,直接给每个参与者发送回滚(rollback)消息;否则,发送提交(commit)消息;参与者根据协调者的指令执行提交或者回滚操作,释放所有事务处理过程中使用的锁资源。(注意:必须在最后阶段释放锁资源) 接下来分两种情况分别讨论提交阶段的过程。
情况1,当所有参与者均反馈yes,提交事务:
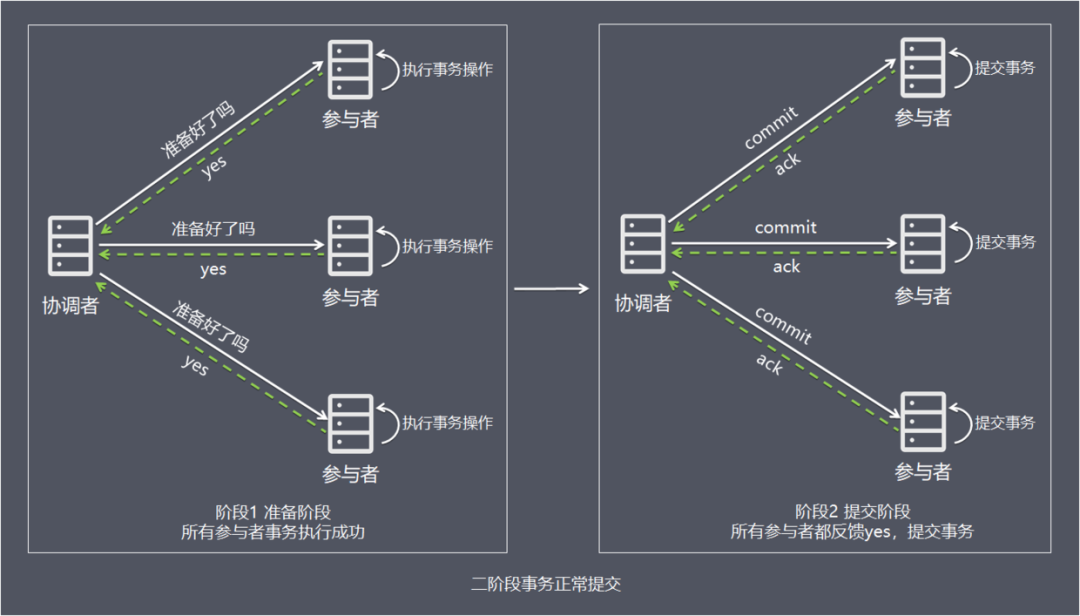
1、协调者向所有参与者发出正式提交事务的请求(即commit请求)。
2、参与者执行commit请求,并释放整个事务期间占用的资源。
3、各参与者向协调者反馈ack(应答)完成的消息。
4、协调者收到所有参与者反馈的ack消息后,即完成事务提交。
情况2,当任何阶段1一个参与者反馈no,中断事务:
1、协调者向所有参与者发出回滚请求(即rollback请求)。
2、参与者使用阶段1中的undo信息执行回滚操作,并释放整个事务期间占用的资源。
3、各参与者向协调者反馈ack完成的消息。
4、协调者收到所有参与者反馈的ack消息后,即完成事务中断。
方案总结
2PC方案实现起来简单,实际项目中使用比较少,主要因为以下问题:
-
性能问题 所有参与者在事务提交阶段处于同步阻塞状态,占用系统资源,容易导致性能瓶颈。
-
可靠性问题 如果协调者存在单点故障问题,如果协调者出现故障,参与者将一直处于锁定状态。
-
数据一致性问题 在阶段2中,如果发生局部网络问题,一部分事务参与者收到了提交消息,另一部分事务参与者没收到提交消息,那么就导致了节点之间数据的不一致。
3PC(三阶段提交)方案
方案简介
三阶段提交协议,是二阶段提交协议的改进版本,与二阶段提交不同的是,引入超时机制。同时在协调者和参与者中都引入超时机制。
三阶段提交将二阶段的准备阶段拆分为2个阶段,插入了一个preCommit阶段,使得原先在二阶段提交中,参与者在准备之后,由于协调者发生崩溃或错误,而导致参与者处于无法知晓是否提交或者中止的“不确定状态”所产生的可能相当长的延时的问题得以解决。
处理流程
阶段1:canCommit 协调者向参与者发送commit请求,参与者如果可以提交就返回yes响应(参与者不执行事务操作),否则返回no响应:
1、协调者向所有参与者发出包含事务内容的canCommit请求,询问是否可以提交事务,并等待所有参与者答复。
2、参与者收到canCommit请求后,如果认为可以执行事务操作,则反馈yes并进入预备状态,否则反馈no。
阶段2:preCommit 协调者根据阶段1 canCommit参与者的反应情况来决定是否可以基于事务的preCommit操作。根据响应情况,有以下两种可能。
情况1:阶段1所有参与者均反馈yes,参与者预执行事务:

1、协调者向所有参与者发出preCommit请求,进入准备阶段。
2、参与者收到preCommit请求后,执行事务操作,将undo和redo信息记入事务日志中(但不提交事务)。
3、各参与者向协调者反馈ack响应或no响应,并等待最终指令。
情况2:阶段1任何一个参与者反馈no,或者等待超时后协调者尚无法收到所有参与者的反馈,即中断事务:
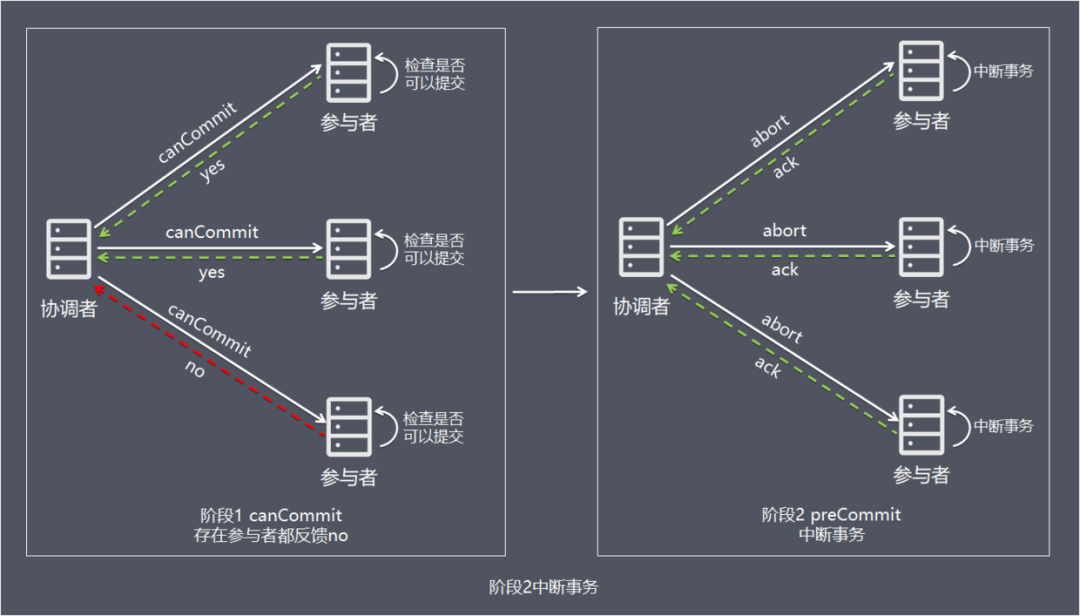
1、协调者向所有参与者发出abort请求。
2、无论收到协调者发出的abort请求,或者在等待协调者请求过程中出现超时,参与者均会中断事务。
阶段3:do Commit 该阶段进行真正的事务提交,也可以分为以下两种情况:
情况1:阶段2所有参与者均反馈ack响应,执行真正的事务提交:
-
1、如果协调者处于工作状态,则向所有参与者发出do Commit请求。
-
2、参与者收到do Commit请求后,会正式执行事务提交,并释放整个事务期间占用的资源。
-
3、各参与者向协调者反馈ack完成的消息。
-
4、协调者收到所有参与者反馈的ack消息后,即完成事务提交。
阶段2任何一个参与者反馈no,或者等待超时后协调者尚无法收到所有参与者的反馈,即中断事务:
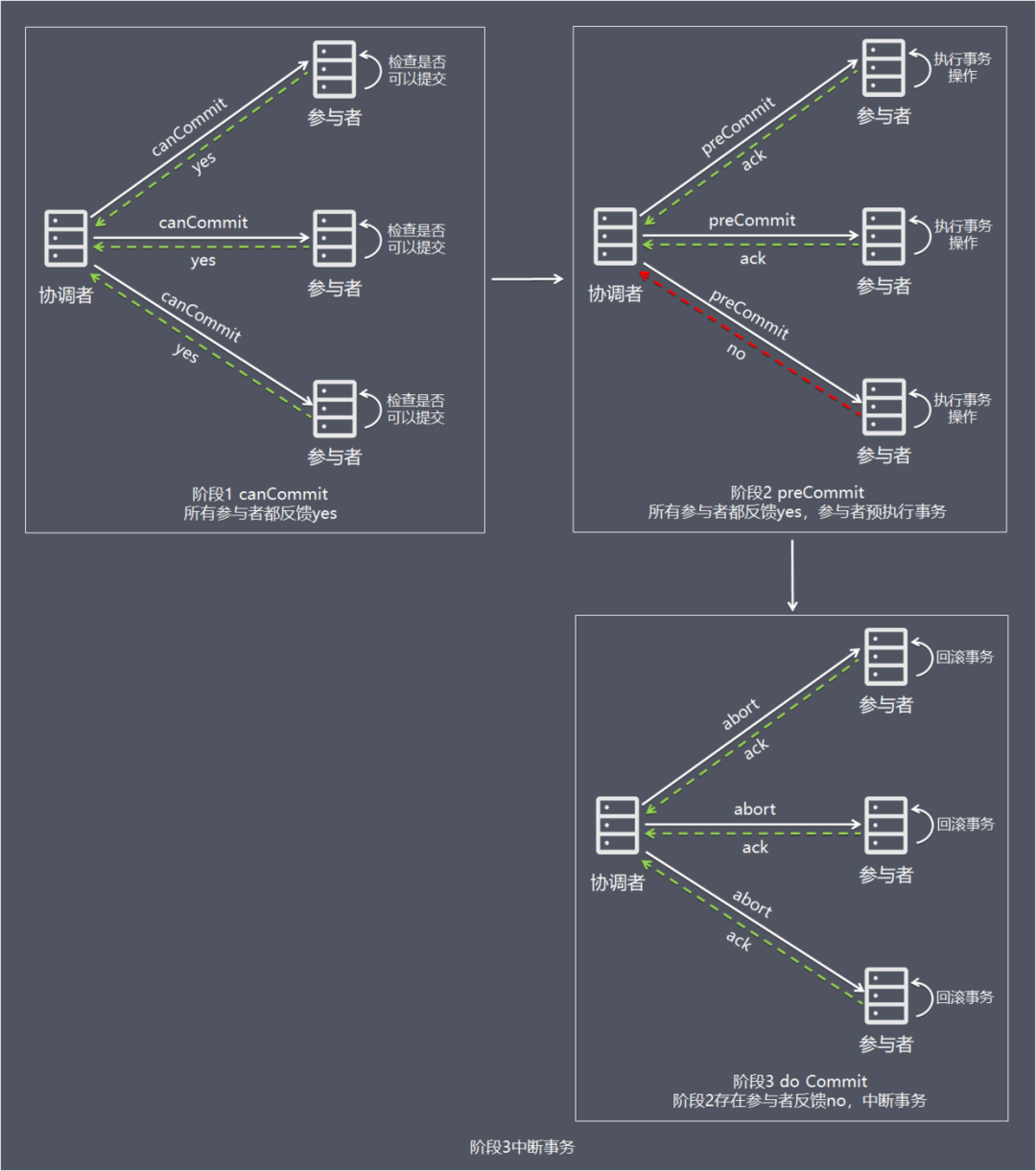
-
1、如果协调者处于工作状态,向所有参与者发出abort请求。
-
2、参与者使用阶段1中的undo信息执行回滚操作,并释放整个事务期间占用的资源。
-
3、各参与者向协调者反馈ack完成的消息。
-
4、协调者收到所有参与者反馈的ack消息后,即完成事务中断。
注意:进入阶段3后,无论协调者出现问题,或者协调者与参与者网络出现问题,都会导致参与者无法接收到协调者发出的do Commit请求或abort请求。此时,参与者都会在等待超时之后,继续执行事务提交。
方案总结
-
优点 相比二阶段提交,三阶段贴近降低了阻塞范围,在等待超时后协调者或参与者会中断事务。避免了协调者单点问题,阶段3中协调者出现问题时,参与者会继续提交事务。
-
缺点 数据不一致问题依然存在,当在参与者收到preCommit请求后等待do commit指令时,此时如果协调者请求中断事务,而协调者无法与参与者正常通信,会导致参与者继续提交事务,造成数据不一致。
TCC (Try-Confirm-Cancel)事务 —— 最终一致性(两阶段型、补偿型)
方案简介
TCC(Try-Confirm-Cancel)的概念,最早是由Pat Helland于2007年发表的一篇名为《Life beyond Distributed Transactions:an Apostate’s Opinion》的论文提出。
TCC是服务化的二阶段编程模型,其Try、Confirm、Cancel 3个方法均由业务编码实现;
-
Try操作作为一阶段,负责资源的检查和预留。
-
Confirm操作作为二阶段提交操作,执行真正的业务。
-
Cancel是预留资源的取消。
TCC事务的Try、Confirm、Cancel可以理解为SQL事务中的Lock、Commit、Rollback。
处理流程
为了方便理解,下面以电商下单为例进行方案解析,这里把整个过程简单分为扣减库存,订单创建2个步骤,库存服务和订单服务分别在不同的服务器节点上。
1、Try 阶段 从执行阶段来看,与传统事务机制中业务逻辑相同。但从业务角度来看,却不一样。TCC机制中的Try仅是一个初步操作,它和后续的确认一起才能真正构成一个完整的业务逻辑,这个阶段主要完成:
-
完成所有业务检查( 一致性 )
-
预留必须业务资源( 准隔离性 )
-
Try 尝试执行业务 TCC事务机制以初步操作(Try)为中心的,确认操作(Confirm)和取消操作(Cancel)都是围绕初步操作(Try)而展开。因此,Try阶段中的操作,其保障性是最好的,即使失败,仍然有取消操作(Cancel)可以将其执行结果撤销。

假设商品库存为100,购买数量为2,这里检查和更新库存的同时,冻结用户购买数量的库存,同时创建订单,订单状态为待确认。
2、Confirm / Cancel 阶段 根据Try阶段服务是否全部正常执行,继续执行确认操作(Confirm)或取消操作(Cancel)。Confirm和Cancel操作满足幂等性,如果Confirm或Cancel操作执行失败,将会不断重试直到执行完成。
Confirm:当Try阶段服务全部正常执行, 执行确认业务逻辑操作
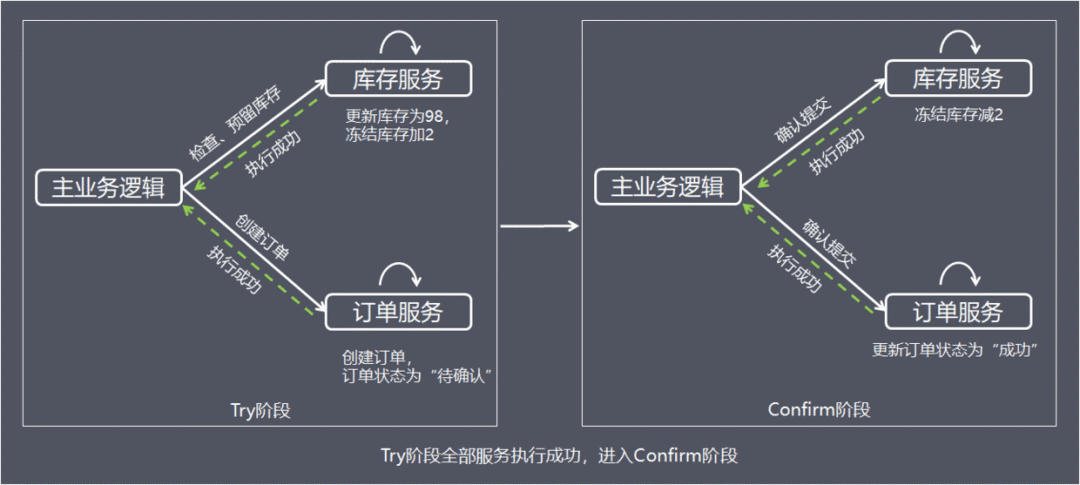
这里使用的资源一定是Try阶段预留的业务资源。在TCC事务机制中认为,如果在Try阶段能正常的预留资源,那Confirm一定能完整正确的提交。Confirm阶段也可以看成是对Try阶段的一个补充,Try+Confirm一起组成了一个完整的业务逻辑。
Cancel:当Try阶段存在服务执行失败, 进入Cancel阶段
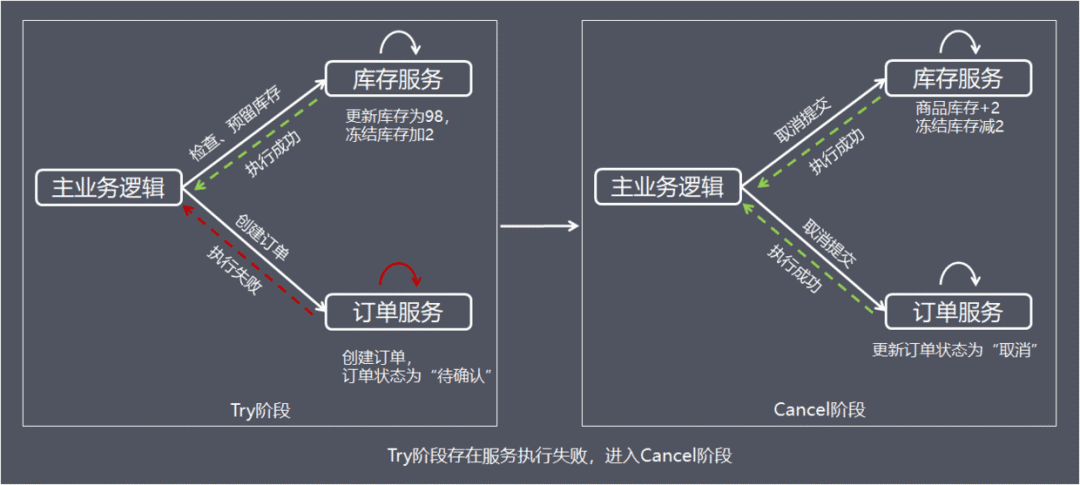
Cancel取消执行,释放Try阶段预留的业务资源,上面的例子中,Cancel操作会把冻结的库存释放,并更新订单状态为取消。
方案总结
TCC事务机制相对于传统事务机制(X/Open XA),TCC事务机制相比于上面介绍的XA事务机制,有以下优点:
-
性能提升 具体业务来实现控制资源锁的粒度变小,不会锁定整个资源。
-
数据最终一致性 基于Confirm和Cancel的幂等性,保证事务最终完成确认或者取消,保证数据的一致性。
-
可靠性 解决了XA协议的协调者单点故障问题,由主业务方发起并控制整个业务活动,业务活动管理器也变成多点,引入集群。
缺点:TCC的Try、Confirm和Cancel操作功能要按具体业务来实现,业务耦合度较高,提高了开发成本。
本地消息表 —— 最终一致性
方案简介
本地消息表的方案最初是由ebay提出,核心思路是将分布式事务拆分成本地事务进行处理。
方案通过在事务主动发起方额外新建事务消息表,事务发起方处理业务和记录事务消息在本地事务中完成,轮询事务消息表的数据发送事务消息,事务被动方基于消息中间件消费事务消息表中的事务。
这样设计可以避免”业务处理成功 + 事务消息发送失败",或"业务处理失败 + 事务消息发送成功"的棘手情况出现,保证2个系统事务的数据一致性。
处理流程
下面把分布式事务最先开始处理的事务方称为事务主动方,在事务主动方之后处理的业务内的其他事务称为事务被动方。
为了方便理解,下面继续以电商下单为例进行方案解析,这里把整个过程简单分为扣减库存,订单创建2个步骤,库存服务和订单服务分别在不同的服务器节点上,其中库存服务是事务主动方,订单服务是事务被动方。
事务的主动方需要额外新建事务消息表,用于记录分布式事务的消息的发生、处理状态。
整个业务处理流程如下:
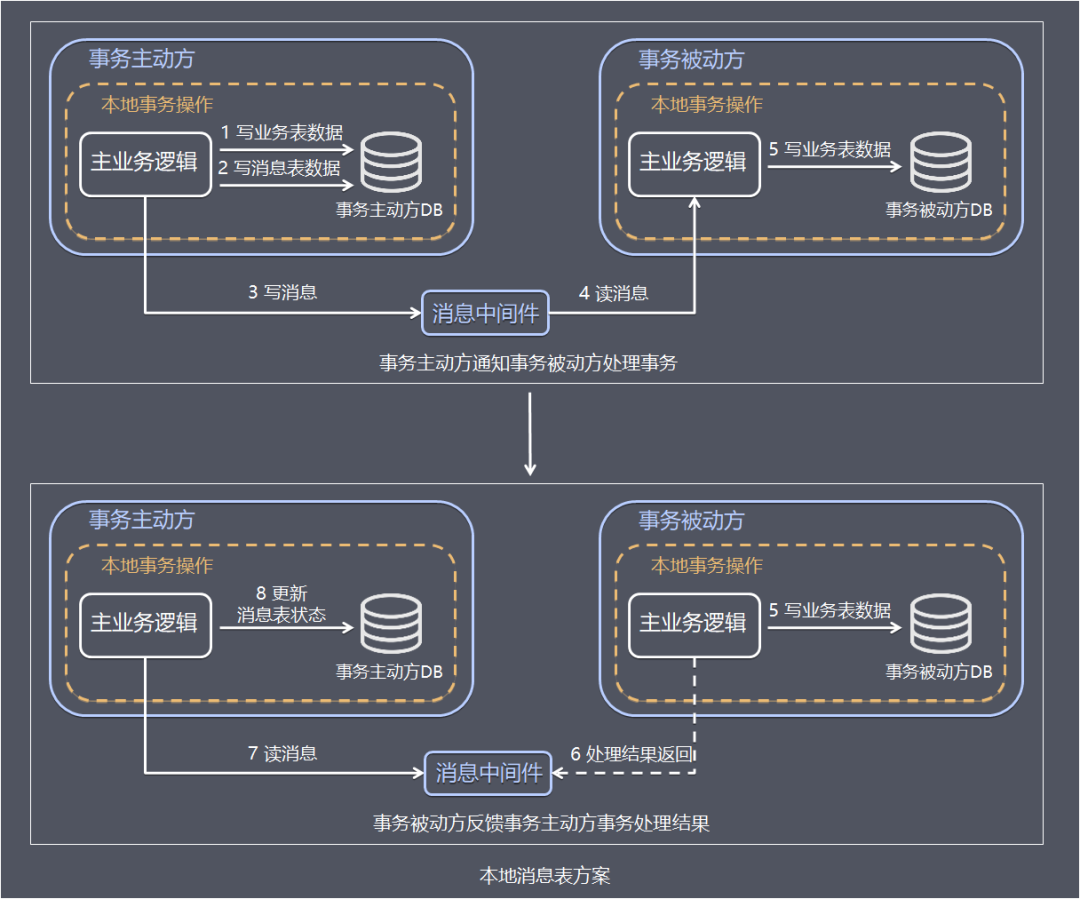
步骤1 事务主动方处理本地事务。 事务主动发在本地事务中处理业务更新操作和写消息表操作。上面例子中库存服务阶段再本地事务中完成扣减库存和写消息表(图中1、2)。
步骤2 事务主动方通过消息中间件,通知事务被动方处理事务通知事务待消息。消息中间件可以基于Kafka、RocketMQ消息队列,事务主动方法主动写消息到消息队列,事务消费方消费并处理消息队列中的消息。上面例子中,库存服务把事务待处理消息写到消息中间件,订单服务消费消息中间件的消息,完成新增订单(图中3 - 5)。
步骤3 事务被动方通过消息中间件,通知事务主动方事务已处理的消息。 上面例子中,订单服务把事务已处理消息写到消息中间件,库存服务消费中间件的消息,并将事务消息的状态更新为已完成(图中6 - 8)
为了数据的一致性,当处理错误需要重试,事务发送方和事务接收方相关业务处理需要支持幂等。具体保存一致性的容错处理如下:
1、当步骤1处理出错,事务回滚,相当于什么都没发生。
2、当步骤2、步骤3处理出错,由于未处理的事务消息还是保存在事务发送方,事务发送方可以定时轮询超时消息数据,再次发送的消息中间件进行处理。事务被动方消费事务消息重试处理。
3、如果是业务上的失败,事务被动方可以发消息给事务主动方进行回滚。
4、如果多个事务被动方已经消费消息,事务主动方需要回滚事务时需要通知事务被动方回滚。
方案总结
方案的优点如下:
-
从应用设计开发的角度实现了消息数据的可靠性,消息数据的可靠性不依赖于消息中间件,弱化了对MQ中间件特性的依赖。
-
方案轻量,容易实现。
缺点如下:
-
与具体的业务场景绑定,耦合性强,不可公用。
-
消息数据与业务数据同库,占用业务系统资源。
-
业务系统在使用关系型数据库的情况下,消息服务性能会受到关系型数据库并发性能的局限。
MQ事务 —— 最终一致(可靠消息,异步确保)
方案简介
基于MQ的分布式事务方案其实是对本地消息表的封装,将本地消息表基于MQ 内部,其他方面的协议基本与本地消息表一致。
处理流程
下面主要基于RocketMQ4.3之后的版本介绍MQ的分布式事务方案。
在本地消息表方案中,保证事务主动方发写业务表数据和写消息表数据的一致性是基于数据库事务,RocketMQ的事务消息相对于普通MQ,相对于提供了2PC的提交接口,方案如下:
正常情况——事务主动方发消息 这种情况下,事务主动方服务正常,没有发生故障,发消息流程如下:
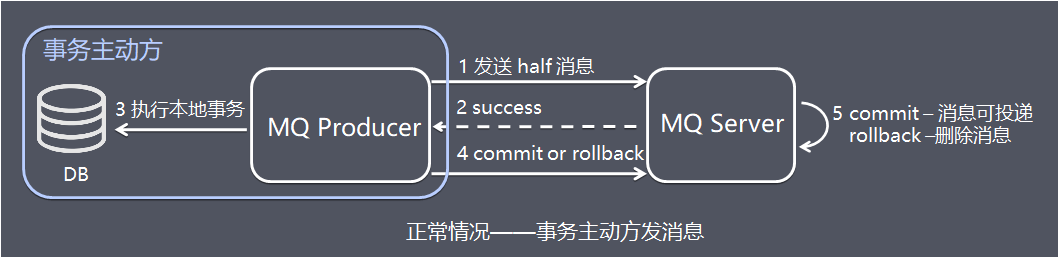
图中1、发送方向 MQ服务端(MQ Server)发送half消息。
图中2、MQ Server 将消息持久化成功之后,向发送方 ACK 确认消息已经发送成功。
图中3、发送方开始执行本地事务逻辑。
图中4、发送方根据本地事务执行结果向 MQ Server 提交二次确认(commit 或是 rollback)。
图中5、MQ Server 收到 commit 状态则将半消息标记为可投递,订阅方最终将收到该消息;MQ Server 收到 rollback 状态则删除半消息,订阅方将不会接受该消息。
异常情况——事务主动方消息恢复 在断网或者应用重启等异常情况下,图中4提交的二次确认超时未到达 MQ Server,此时处理逻辑如下:
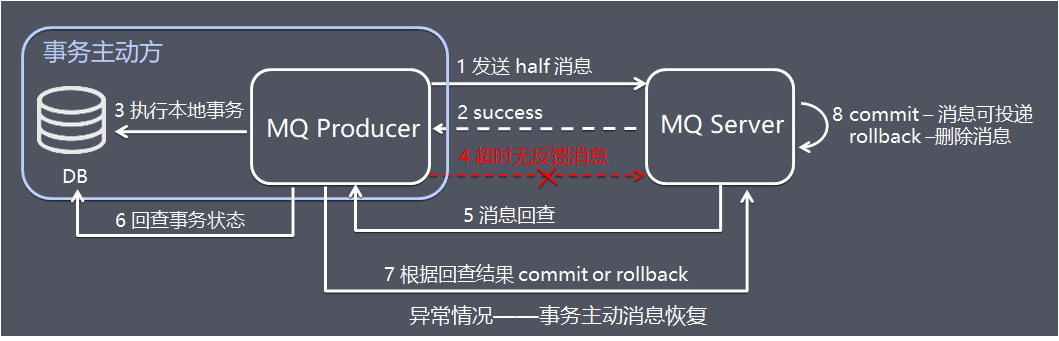
图中5、MQ Server 对该消息发起消息回查。
图中6、发送方收到消息回查后,需要检查对应消息的本地事务执行的最终结果。
图中7、发送方根据检查得到的本地事务的最终状态再次提交二次确认
图中8、MQ Server基于commit / rollback 对消息进行投递或者删除
方案总结
相比本地消息表方案,MQ事务方案优点是:
-
消息数据独立存储 ,降低业务系统与消息系统之间的耦合。
-
吞吐量由于使用本地消息表方案。
缺点是:
-
一次消息发送需要两次网络请求(half消息 + commit/rollback消息)
-
业务处理服务需要实现消息状态回查接口
最大努力通知(非可靠消息,定期校对)
最大努力通知也被称为定期校对,其实在MQ事务已经包含,这里再单独介绍,主要是为了知识体系的完整性。这种方案也需要消息中间件的参与,其过程如下:
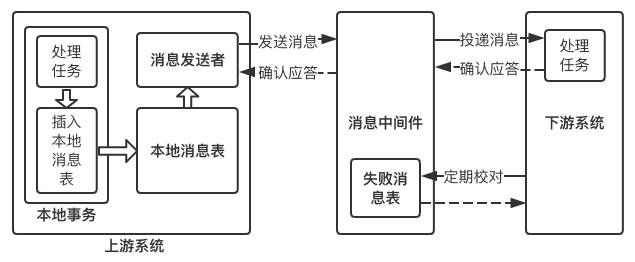
-
上游系统在完成任务后,向消息中间件同步地发送一条消息,确保消息中间件成功持久化这条消息,然后上游系统可以去做别的事情了;
-
消息中间件收到消息后负责将该消息同步投递给相应的下游系统,并触发下游系统的任务执行;
-
当下游系统处理成功后,向消息中间件反馈确认应答,消息中间件便可以将该条消息删除,从而该事务完成。
上面是一个理想化的过程,但在实际场景中,往往会出现如下几种意外情况:
-
消息中间件向下游系统投递消息失败
-
上游系统向消息中间件发送消息失败
对于第一种情况,消息中间件具有重试机制,我们可以在消息中间件中设置消息的重试次数和重试时间间隔,对于网络不稳定导致的消息投递失败的情况,往往重试几次后消息便可以成功投递,如果超过了重试的上限仍然投递失败,那么消息中间件不再投递该消息,而是记录在失败消息表中,消息中间件需要提供失败消息的查询接口,下游系统会定期查询失败消息,并将其消费,这就是所谓的“定期校对”。
如果重复投递和定期校对都不能解决问题,往往是因为下游系统出现了严重的错误,此时就需要人工干预。
对于第二种情况,需要在上游系统中建立消息重发机制。可以在上游系统建立一张本地消息表,并将 任务处理过程 和 向本地消息表中插入消息 这两个步骤放在一个本地事务中完成。如果向本地消息表插入消息失败,那么就会触发回滚,之前的任务处理结果就会被取消。如果这两步都执行成功,那么该本地事务就完成了。接下来会有一个专门的消息发送者不断地发送本地消息表中的消息,如果发送失败它会返回重试。当然,也要给消息发送者设置重试的上限,一般而言,达到重试上限仍然发送失败,那就意味着消息中间件出现严重的问题,此时也只有人工干预才能解决问题。
对于不支持事务型消息的消息中间件,如果要实现分布式事务的话,就可以采用这种方式。它能够通过重试机制+定期校对实现分布式事务,但相比于第二种方案,它达到数据一致性的周期较长,而且还需要在上游系统中实现消息重试发布机制,以确保消息成功发布给消息中间件,这无疑增加了业务系统的开发成本,使得业务系统不够纯粹,并且这些额外的业务逻辑无疑会占用业务系统的硬件资源,从而影响性能。
因此,尽量选择支持事务型消息的消息中间件来实现分布式事务,如RocketMQ。
Saga事务 —— 最终一致性
方案简介
Saga事务源于1987年普林斯顿大学的Hecto和Kenneth发表的如何处理long lived transaction(长活事务)论文,Saga事务核心思想是将长事务拆分为多个本地短事务,由Saga事务协调器协调,如果正常结束那就正常完成,如果某个步骤失败,则根据相反顺序一次调用补偿操作。
处理流程
Saga事务基本协议如下:
-
每个Saga事务由一系列幂等的有序子事务(sub-transaction) Ti 组成。
-
每个Ti 都有对应的幂等补偿动作Ci,补偿动作用于撤销Ti造成的结果。
可以看到,和TCC相比,Saga没有“预留”动作,它的Ti就是直接提交到库。
下面以下单流程为例,整个操作包括:创建订单、扣减库存、支付、增加积分 Saga的执行顺序有两种:

-
事务正常执行完成 T1, T2, T3, ..., Tn,例如:扣减库存(T1),创建订单(T2),支付(T3),依次有序完成整个事务。
-
事务回滚 T1, T2, ..., Tj, Cj,..., C2, C1,其中0 < j < n,例如:扣减库存(T1),创建订单(T2),支付(T3,支付失败),支付回滚(C3),订单回滚(C2),恢复库存(C1)。
Saga定义了两种恢复策略:
-
向前恢复(forward recovery)
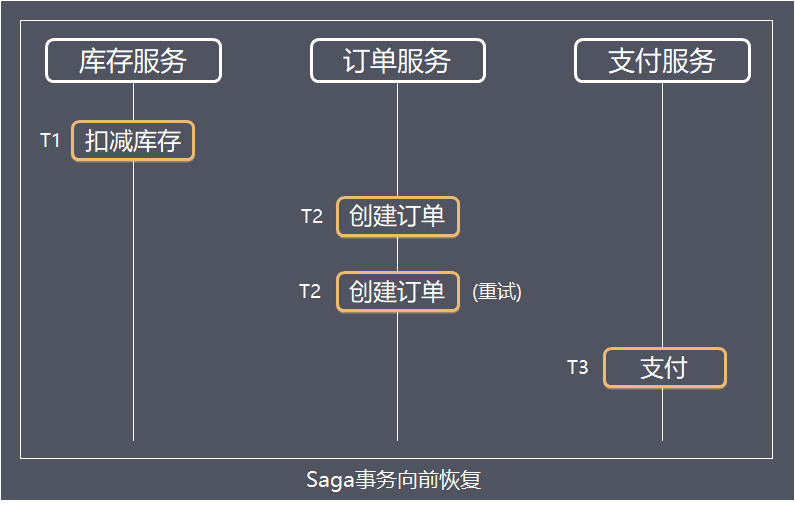
对应于上面第一种执行顺序,适用于必须要成功的场景,发生失败进行重试,执行顺序是类似于这样的:T1, T2, ..., Tj(失败), Tj(重试),..., Tn,其中j是发生错误的子事务(sub-transaction)。该情况下不需要Ci。
-
向后恢复(backward recovery)
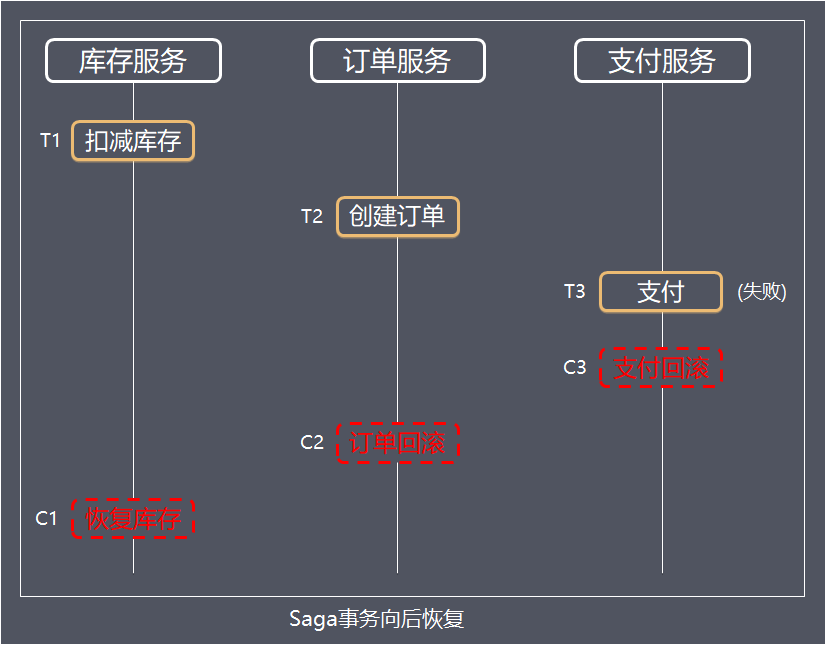
对应于上面提到的第二种执行顺序,其中j是发生错误的子事务(sub-transaction),这种做法的效果是撤销掉之前所有成功的子事务,使得整个Saga的执行结果撤销。
Saga事务常见的有两种不同的实现方式:
-
1、命令协调(Order Orchestrator):中央协调器负责集中处理事件的决策和业务逻辑排序。
中央协调器(Orchestrator,简称OSO)以命令/回复的方式与每项服务进行通信,全权负责告诉每个参与者该做什么以及什么时候该做什么。
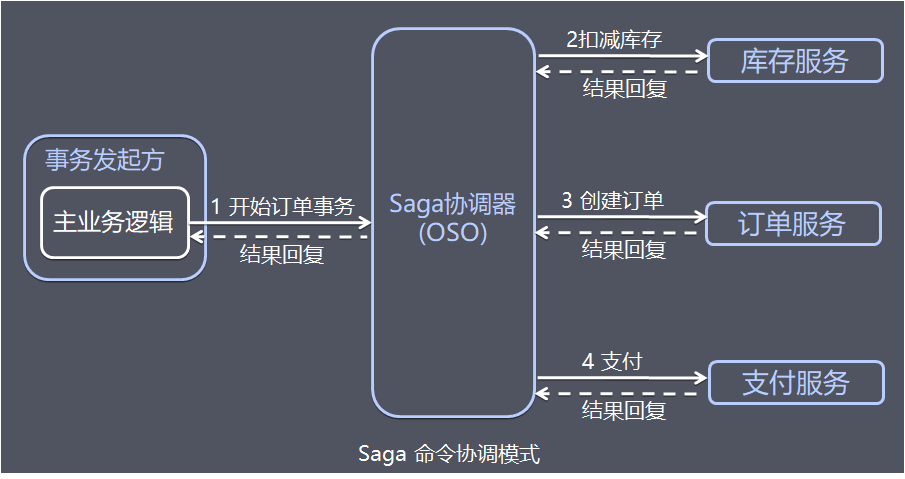
以电商订单的例子为例:
1、事务发起方的主业务逻辑请求OSO服务开启订单事务 2、OSO向库存服务请求扣减库存,库存服务回复处理结果。3、OSO向订单服务请求创建订单,订单服务回复创建结果。4、OSO向支付服务请求支付,支付服务回复处理结果。5、主业务逻辑接收并处理OSO事务处理结果回复。
中央协调器必须事先知道执行整个订单事务所需的流程(例如通过读取配置)。如果有任何失败,它还负责通过向每个参与者发送命令来撤销之前的操作来协调分布式的回滚。基于中央协调器协调一切时,回滚要容易得多,因为协调器默认是执行正向流程,回滚时只要执行反向流程即可。
-
2、事件编排 (Event Choreography0:没有中央协调器(没有单点风险)时,每个服务产生并观察其他服务的事件,并决定是否应采取行动。
在事件编排方法中,第一个服务执行一个事务,然后发布一个事件。该事件被一个或多个服务进行监听,这些服务再执行本地事务并发布(或不发布)新的事件。
当最后一个服务执行本地事务并且不发布任何事件时,意味着分布式事务结束,或者它发布的事件没有被任何Saga参与者听到都意味着事务结束。
以电商订单的例子为例:
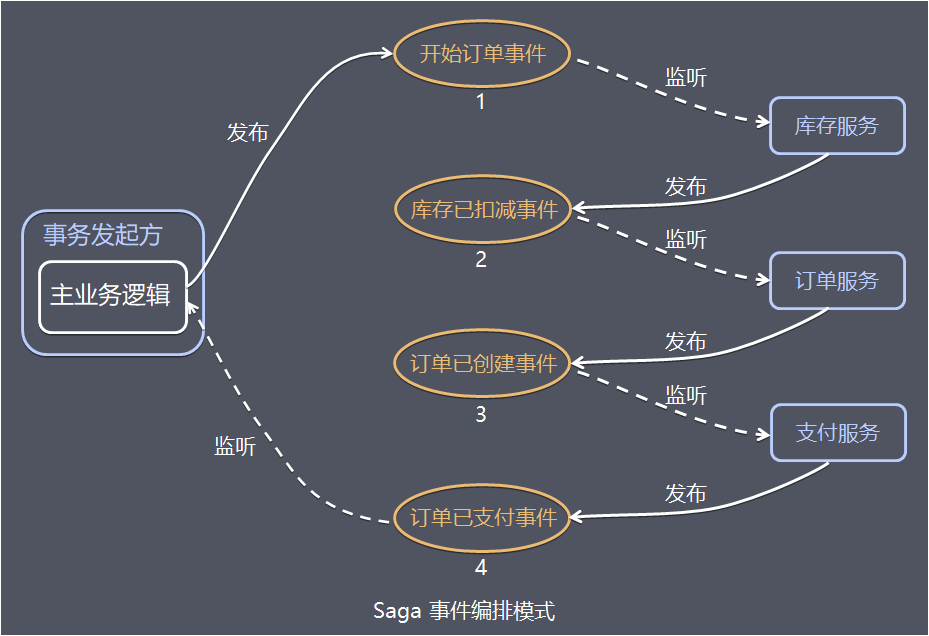
1、事务发起方的主业务逻辑发布开始订单事件 2、库存服务监听开始订单事件,扣减库存,并发布库存已扣减事件 2、订单服务监听库存已扣减事件,创建订单,并发布订单已创建事件 4、支付服务监听订单已创建事件,进行支付,并发布订单已支付事件 5、主业务逻辑监听订单已支付事件并处理。
事件/编排是实现Saga模式的自然方式,它很简单,容易理解,不需要太多的代码来构建。如果事务涉及2至4个步骤,则可能是非常合适的。
方案总结
命令协调设计的优点和缺点: 优点如下:
-
1、服务之间关系简单,避免服务之间的循环依赖关系,因为Saga协调器会调用Saga参与者,但参与者不会调用协调器
-
2、程序开发简单,只需要执行命令/回复(其实回复消息也是一种事件消息),降低参与者的复杂性。
-
3、易维护扩展,在添加新步骤时,事务复杂性保持线性,回滚更容易管理,更容易实施和测试
缺点如下:
-
1、中央协调器容易处理逻辑容易过于复杂,导致难以维护。
-
2、存在协调器单点故障风险。
事件/编排设计的优点和缺点 优点如下:
-
1、避免中央协调器单点故障风险。
-
2、当涉及的步骤较少服务开发简单,容易实现。
缺点如下:
-
1、服务之间存在循环依赖的风险。
-
2、当涉及的步骤较多,服务间关系混乱,难以追踪调测。
值得补充的是,由于Saga模型中没有Prepare阶段,因此事务间不能保证隔离性,当多个Saga事务操作同一资源时,就会产生更新丢失、脏数据读取等问题,这时需要在业务层控制并发,例如:在应用层面加锁,或者应用层面预先冻结资源。
总结
各方案使用场景
介绍完分布式事务相关理论和常见解决方案后,最终的目的在实际项目中运用,因此,总结一下各个方案的常见的使用场景。
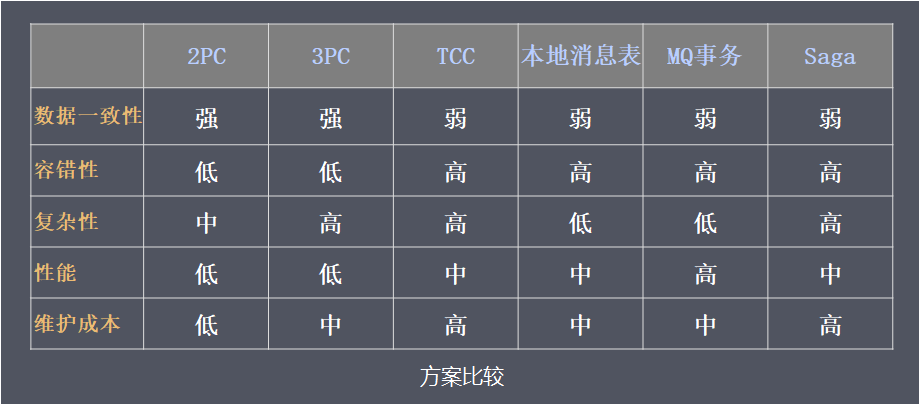
-
2PC/3PC 依赖于数据库,能够很好的提供强一致性和强事务性,但相对来说延迟比较高,比较适合传统的单体应用,在同一个方法中存在跨库操作的情况,不适合高并发和高性能要求的场景。
-
TCC 适用于执行时间确定且较短,实时性要求高,对数据一致性要求高,比如互联网金融企业最核心的三个服务:交易、支付、账务。
-
本地消息表/MQ事务 都适用于事务中参与方支持操作幂等,对一致性要求不高,业务上能容忍数据不一致到一个人工检查周期,事务涉及的参与方、参与环节较少,业务上有对账/校验系统兜底。
-
Saga事务 由于Saga事务不能保证隔离性,需要在业务层控制并发,适合于业务场景事务并发操作同一资源较少的情况。Saga相比缺少预提交动作,导致补偿动作的实现比较麻烦,例如业务是发送短信,补偿动作则得再发送一次短信说明撤销,用户体验比较差。Saga事务较适用于补偿动作容易处理的场景。
常用的分布式事务解决方案
-
TCC (两阶段型、补偿型)
-
MQ事务,可靠消息最终一致(异步确保型)
-
最大努力通知(非可靠消息 、定期校对)
三种解决方案均是基于柔性事务实现最终一致性。
TCC事务补偿型方案,采用两阶段实现,但有别于2PC协议的两阶段提交,实时性较高,基于AOP实现,适合于实时的系统交互。
异步消息确保型方案,基于MQ中间件实现,或者说是对MQ不支持分布式事务进行的改进,使用场景比较广,适合于对实时性要求不高的应用场景。
最大努力通知型方案,适合于跨平台的业务活动,例如商户通知,允许多次通知、支持查询校对、定期对账。
分布式事务方案设计
实际运用理论时进行架构设计时,许多人容易犯“手里有了锤子,看什么都觉得像钉子”的错误,设计方案时考虑的问题场景过多,各种重试,各种补偿机制引入系统,导致设计出来的系统过于复杂,落地遥遥无期。
世界上解决一个计算机问题最简单的方法:“恰好”不需要解决它!—— 阿里中间件技术专家沈询
有些问题,看起来很重要,但实际上我们可以通过合理的设计或者将问题分解来规避。设计分布式事务系统也不是需要考虑所有异常情况,不必过度设计各种回滚,补偿机制。如果硬要把时间花在解决问题本身,实际上不仅效率低下,而且也是一种浪费。
如果系统要实现回滚流程的话,有可能系统复杂度将大大提升,且很容易出现Bug,估计出现Bug的概率会比需要事务回滚的概率大很多。在设计系统时,我们需要衡量是否值得花这么大的代价来解决这样一个出现概率非常小的问题,可以考虑当出现这个概率很小的问题,能否采用人工解决的方式,这也是大家在解决疑难问题时需要多多思考的地方。
分布式锁
分布式锁的实现方式
| 类别 | 优点 | 缺点 |
|---|---|---|
| 基于数据库实现分布式锁 | 操作简单,容易理解 | 1.性能较差,并且有锁表的风险;2.非阻塞操作失败后,需要轮询,占用cpu资源;3.长时间不commit或者长时间轮询,可能会占用较多连接资源 |
| 基于缓存(Redis等)实现分布式锁 | 非阻塞,性能好 | 1.锁删除失败,过期时间不好控制,操作不当容易造成死锁2.非阻塞,操作失败后,需要轮询,占用cpu资源; |
| 基于Zookeeper实现分布式锁 | ZooKeeper有较好的性能和可靠性。集群,无单点问题,可重入,可避免锁无法释放 | 性能不如redis实现,主要原因是写操作(获取锁释放锁)都需要在Leader上执行,然后同步到follower。 |
从理解的难易程度角度(从低到高)数据库 > 缓存 > Zookeeper
从实现的复杂性角度(从低到高)Zookeeper >= 缓存 > 数据库
从性能角度(从高到低)缓存 > Zookeeper >= 数据库
从可靠性角度(从高到低)Zookeeper > 缓存 > 数据库
数据结构与算法
冒泡排序
冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列,依次比较两个元素,如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
算法描述
-
比较相邻的元素。如果第一个比第二个大,就交换它们两个;
-
对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
-
针对所有的元素重复以上的步骤,除了最后一个;
-
重复步骤1~3,直到排序完成。
动图演示
代码实现
下面的排序算法统一使用的测试代码如下,源码GitHub链接
public static void main(String[] args) {
int[] array = {3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48};
// 只需要修改成对应的方法名就可以了
bubbleSort(array);
System.out.println(Arrays.toString(array));
}
/**
* Description:冒泡排序
*
* @param array 需要排序的数组
* @author JourWon
* @date 2019/7/11 9:54
*/
public static void bubbleSort(int[] array) {
if (array == null || array.length <= 1) {
return;
}
int length = array.length;
// 外层循环控制比较轮数i
for (int i = 0; i < length; i++) {
// 内层循环控制每一轮比较次数,每进行一轮排序都会找出一个较大值
// (array.length - 1)防止索引越界,(array.length - 1 - i)减少比较次数
for (int j = 0; j < length - 1 - i; j++) {
// 前面的数大于后面的数就进行交换
if (array[j] > array[j + 1]) {
int temp = array[j + 1];
array[j + 1] = array[j];
array[j] = temp;
}
}
}
}
算法分析
最佳情况:T(n) = O(n) 最差情况:T(n) = O(n^2) 平均情况:T(n) = O(n^2)
选择排序
表现最稳定的排序算法之一,因为无论什么数据进去都是O(n^2)的时间复杂度,所以用到它的时候,数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。理论上讲,选择排序可能也是平时排序一般人想到的最多的排序方法了吧。
选择排序(Selection-sort)是一种简单直观的排序算法。它的工作原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
算法描述
n个记录的直接选择排序可经过n-1趟直接选择排序得到有序结果。具体算法描述如下:
-
初始状态:无序区为R[1..n],有序区为空;
-
第i趟排序(i=1,2,3…n-1)开始时,当前有序区和无序区分别为R[1..i-1]和R(i..n)。该趟排序从当前无序区中-选出关键字最小的记录 R[k],将它与无序区的第1个记录R交换,使R[1..i]和R[i+1..n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区;
-
n-1趟结束,数组有序化了。
动图演示
![]()
代码实现
下面的排序算法统一使用的测试代码如下,源码GitHub链接
public static void main(String[] args) {
int[] array = {3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48};
// 只需要修改成对应的方法名就可以了
selectionSort(array);
System.out.println(Arrays.toString(array));
}
/**
* Description: 选择排序
*
* @param array
* @return void
* @author JourWon
* @date 2019/7/11 23:31
*/
public static void selectionSort(int[] array) {
if (array == null || array.length <= 1) {
return;
}
int length = array.length;
for (int i = 0; i < length - 1; i++) {
// 保存最小数的索引
int minIndex = i;
for (int j = i + 1; j < length; j++) {
// 找到最小的数
if (array[j] < array[minIndex]) {
minIndex = j;
}
}
// 交换元素位置
if (i != minIndex) {
swap(array, minIndex, i);
}
}
}
/**
* Description: 交换元素位置
*
* @param array
* @param a
* @param b
* @return void
* @author JourWon
* @date 2019/7/11 17:57
*/
private static void swap(int[] array, int a, int b) {
int temp = array[a];
array[a] = array[b];
array[b] = temp;
}
算法分析
最佳情况:T(n) = O(n^2) 最差情况:T(n) = O(n^2) 平均情况:T(n) = O(n^2)
快速排序
快速排序的基本思想:通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
算法描述
快速排序使用分治法来把一个串(list)分为两个子串(sub-lists)。具体算法描述如下:
-
从数列中挑出一个元素,称为 “基准”(pivot);
-
重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
-
递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
动图演示
![]()
代码实现
下面的排序算法统一使用的测试代码如下,源码GitHub链接
public static void main(String[] args) {
int[] array = {3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48};
// 只需要修改成对应的方法名就可以了
quickSort(array);
System.out.println(Arrays.toString(array));
}
/**
* Description: 快速排序
*
* @param array
* @return void
* @author JourWon
* @date 2019/7/11 23:39
*/
public static void quickSort(int[] array) {
quickSort(array, 0, array.length - 1);
}
private static void quickSort(int[] array, int left, int right) {
if (array == null || left >= right || array.length <= 1) {
return;
}
int mid = partition(array, left, right);
quickSort(array, left, mid);
quickSort(array, mid + 1, right);
}
private static int partition(int[] array, int left, int right) {
int temp = array[left];
while (right > left) {
// 先判断基准数和后面的数依次比较
while (temp <= array[right] && left < right) {
--right;
}
// 当基准数大于了 arr[left],则填坑
if (left < right) {
array[left] = array[right];
++left;
}
// 现在是 arr[right] 需要填坑了
while (temp >= array[left] && left < right) {
++left;
}
if (left < right) {
array[right] = array[left];
--right;
}
}
array[left] = temp;
return left;
}
算法分析
最佳情况:T(n) = O(nlogn) 最差情况:T(n) = O(n^2) 平均情况:T(n) = O(nlogn)
递归
什么叫递归
递归函数就是直接或间接调用自身的函数,也就是自身调用自己。
一般什么时候使用递归?
递归是常用的编程技术,其基本思想就是“自己调用自己”,一个使用递归技术的方法即是直接或间接的调用自身的方法。递归方法实际上体现了“以此类推”、“用同样的步骤重复”这样的思想。
还有些数据结构如二叉树,结构本身固有递归特性;此外,有一类问题,其本身没有明显的递归结构,但用递归程序求解比其他方法更容易编写程序。
需满足的两个条件
-
有反复执行的过程(调用自身)
-
有跳出反复执行过程的条件(递归出口)
经典问题:阶乘
递归阶乘n! = n * (n-1) * (n-2) * ...* 1(n>0)
public static Integer recursionMulity(Integer n) {
if (n == 1) {
return 1;
}
return n * recursionMulity(n - 1);
}
经典问题:不死神兔(斐波那契数列)
3个月起每个月都生一对兔子,小兔子长到第三个月后每个月又生一对兔子,假如兔子都不死,问每个月的兔子总数为多少?
分析:首先我们要明白题目的意思指的是每个月的兔子总对数;假设将兔子分为小中大三种,兔子从出生后三个月后每个月就会生出一对兔子,
那么我们假定第一个月的兔子为小兔子,第二个月为中兔子,第三个月之后就为大兔子,那么第一个月分别有1、0、0,第二个月分别为0、1、0,
第三个月分别为1、0、1,第四个月分别为,1、1、1,第五个月分别为2、1、2,第六个月分别为3、2、3,第七个月分别为5、3、5……
兔子总数分别为:1、1、2、3、5、8、13……
于是得出了一个规律,从第三个月起,后面的兔子总数都等于前面两个月的兔子总数之和,即为斐波那契数列。
public static int fib(int mon) {
if (mon < 2) {
return 1;
} else {
return fib(mon - 1) + fib(mon - 2);
}
}
二分查找
在数组[130,150,170,190,210,230,250,270,290,310]中查找数字190,红色为二分线(折半线),灰色为查找区域,黑色为排除区域。
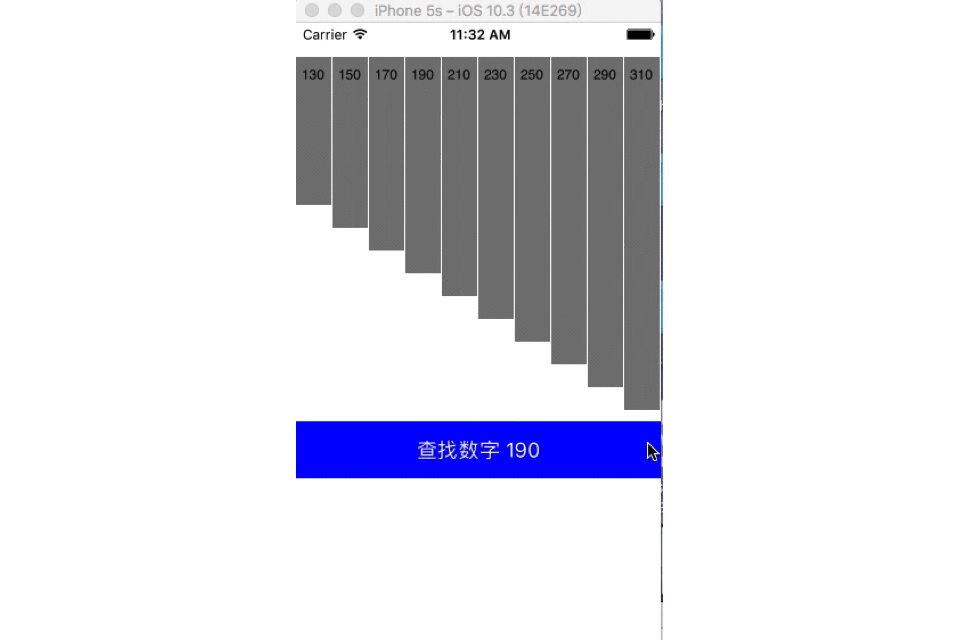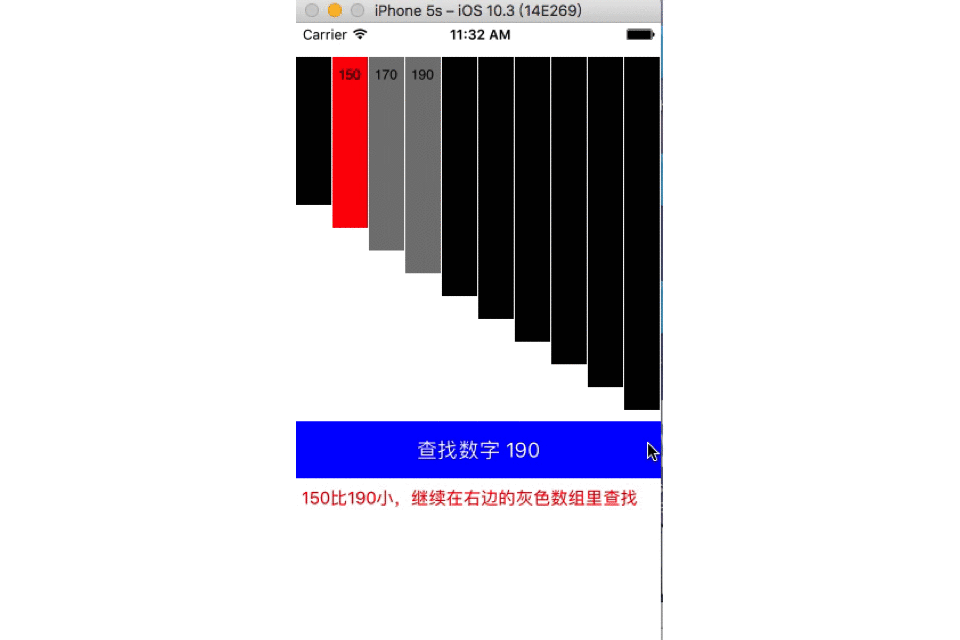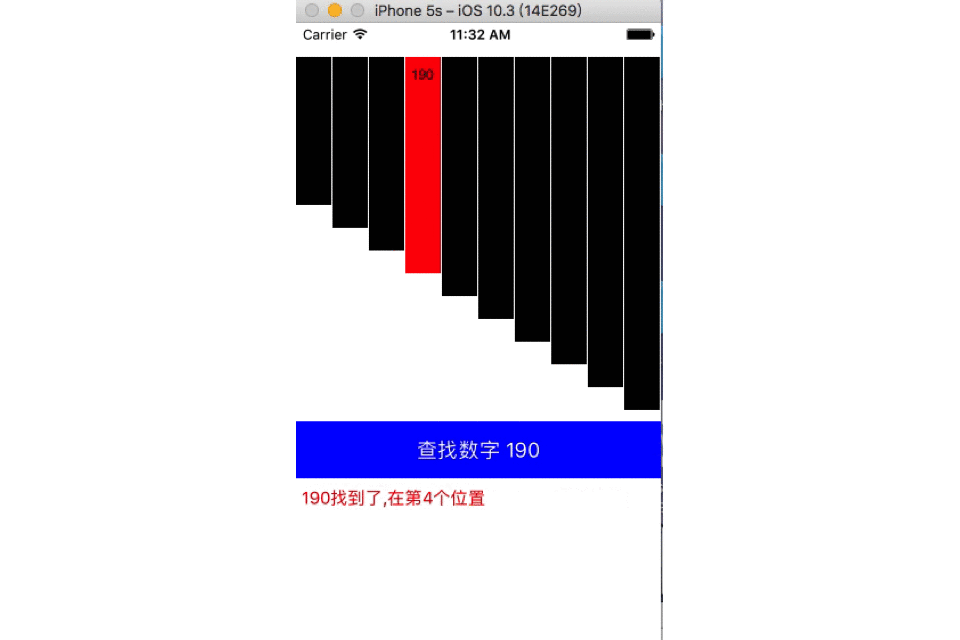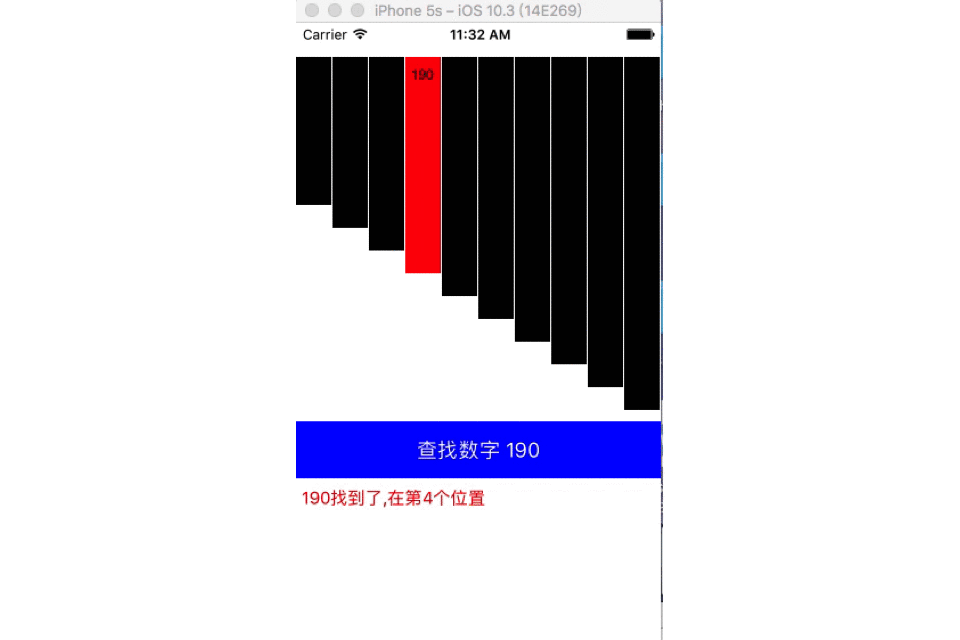
二分查找也称折半查找(Binary Search),它是一种效率较高的查找方法,前提是数据结构必须先排好序,时间复杂度可以表示O(h)=O(log2n),以2为底,n的对数。其缺点是要求待查表为有序表,且插入删除困难。
左加右不加,找右缩左,找左缩右
public class BinarySearch {
public static void main(String[] args) {
int[] arr = {5, 12, 23, 43, 66, 98, 100};
System.out.println(binarySearch(arr, 23));
}
/**
* 循环实现二分查找
*
* @param arr
* @param key
* @return
*/
public static int binarySearch(int[] arr, int key) {
//第一个下标
int low = 0;
//最后一个下标
int high = arr.length - 1;
int mid = 0;
//防越界
if (key < arr[low] || key > arr[high] || low > high) {
return -1;
}
while (low <= high) {
mid = low + (high – low) / 2;
if (key < arr[mid]) {
high = mid - 1;
} else if (key > arr[mid]) {
low = mid + 1;
} else {
return mid;
}
}
return -1;
}
}
二分查找中中间值的计算
这是一个经典的话题,如何计算二分查找中的中值?大家一般给出了两种计算方法:
-
算法一:
mid = (low + high) / 2 -
算法二:
mid = low + (high – low)/2
乍看起来,算法一简洁,算法二提取之后,跟算法一没有什么区别。但是实际上,区别是存在的。算法一的做法,在极端情况下,(low + high)存在着溢出的风险,进而得到错误的mid结果,导致程序错误。而算法二能够保证计算出来的mid,一定大于low,小于high,不存在溢出的问题。
一致性Hash算法
概述
一致性Hash是一种特殊的Hash算法,由于其均衡性、持久性的映射特点,被广泛的应用于负载均衡领域和分布式存储,如nginx和memcached都采用了一致性Hash来作为集群负载均衡的方案。
普通的Hash函数最大的作用是散列,或者说是将一系列在形式上具有相似性质的数据,打散成随机的、均匀分布的数据。不难发现,这样的Hash只要集群的数量N发生变化,之前的所有Hash映射就会全部失效。如果集群中的每个机器提供的服务没有差别,倒不会产生什么影响,但对于分布式缓存这样的系统而言,映射全部失效就意味着之前的缓存全部失效,后果将会是灾难性的。一致性Hash通过构建环状的Hash空间代替线性Hash空间的方法解决了这个问题。
良好的分布式cahce系统中的一致性hash算法应该满足以下几个方面:
-
平衡性(Balance)
平衡性是指哈希的结果能够尽可能分布到所有的缓冲中去,这样可以使得所有的缓冲空间都得到利用。很多哈希算法都能够满足这一条件。
-
单调性(Monotonicity)
单调性是指如果已经有一些内容通过哈希分派到了相应的缓冲中,又有新的缓冲区加入到系统中,那么哈希的结果应能够保证原有已分配的内容可以被映射到新的缓冲区中去,而不会被映射到旧的缓冲集合中的其他缓冲区。
-
分散性(Spread)
在分布式环境中,终端有可能看不到所有的缓冲,而是只能看到其中的一部分。当终端希望通过哈希过程将内容映射到缓冲上时,由于不同终端所见的缓冲范围有可能不同,从而导致哈希的结果不一致,最终的结果是相同的内容被不同的终端映射到不同的缓冲区中。这种情况显然是应该避免的,因为它导致相同内容被存储到不同缓冲中去,降低了系统存储的效率。分散性的定义就是上述情况发生的严重程度。好的哈希算法应能够尽量避免不一致的情况发生,也就是尽量降低分散性。
-
负载(Load)
负载问题实际上是从另一个角度看待分散性问题。既然不同的终端可能将相同的内容映射到不同的缓冲区中,那么对于一个特定的缓冲区而言,也可能被不同的用户映射为不同的内容。与分散性一样,这种情况也是应当避免的,因此好的哈希算法应能够尽量降低缓冲的负荷。
-
平滑性(Smoothness)
平滑性是指缓存服务器的数目平滑改变和缓存对象的平滑改变是一致的。
一致性Hash算法原理
简单来说,一致性哈希将整个哈希值空间组织成一个虚拟的圆环,如假设某哈希函数H的值空间为0-2^32-1(即哈希值是一个32位无符号整形),整个哈希空间环如下:整个空间按顺时针方向组织。0和2^32-1在零点中方向重合。
![]()
下一步将各个服务器使用Hash进行一次哈希,具体可以选择服务器的ip或主机名作为关键字进行哈希,这样每台机器就能确定其在哈希环上的位置,这里假设将上文中四台服务器使用ip地址哈希后在环空间的位置如下:
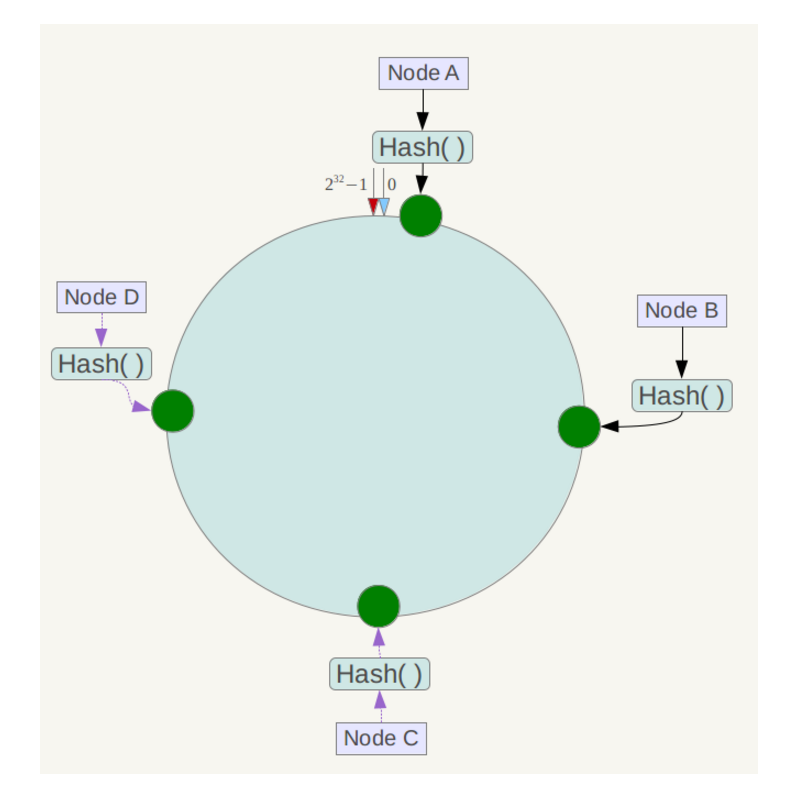
接下来使用如下算法定位数据访问到相应服务器:将数据key使用相同的函数Hash计算出哈希值,并确定此数据在环上的位置,从此位置沿环顺时针“行走”,第一台遇到的服务器就是其应该定位到的服务器。
例如我们有Object A、Object B、Object C、Object D四个数据对象,经过哈希计算后,在环空间上的位置如下:
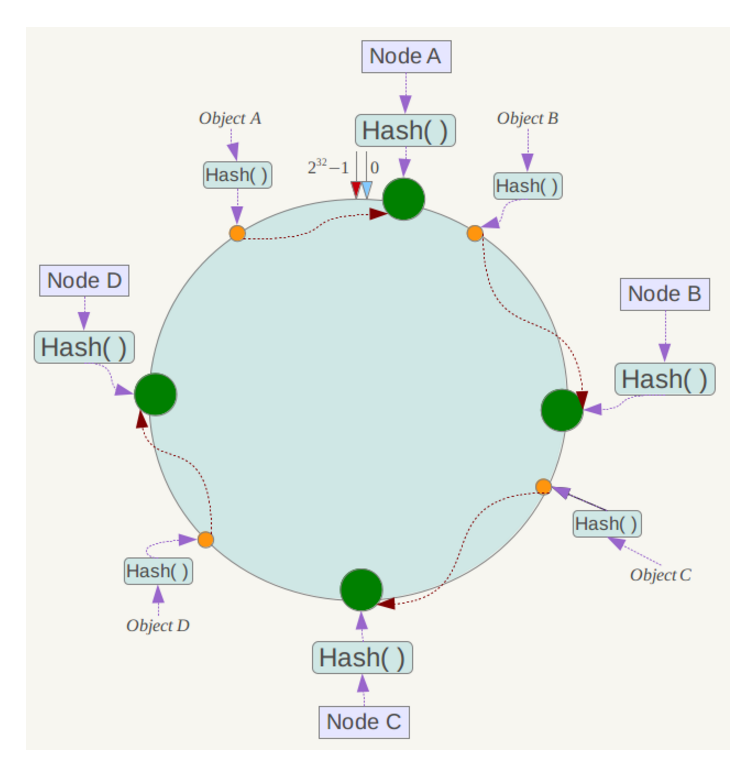
根据一致性哈希算法,数据A会被定为到Node A上,B被定为到Node B上,C被定为到Node C上,D被定为到Node D上。
下面分析一致性哈希算法的容错性和可扩展性。现假设Node C不幸宕机,可以看到此时对象A、B、D不会受到影响,只有C对象被重定位到Node D。一般的,在一致性哈希算法中,如果一台服务器不可用,则受影响的数据仅仅是此服务器到其环空间中前一台服务器(即沿着逆时针方向行走遇到的第一台服务器)之间数据,其它不会受到影响。
下面考虑另外一种情况,如果在系统中增加一台服务器Node X,如下图所示:
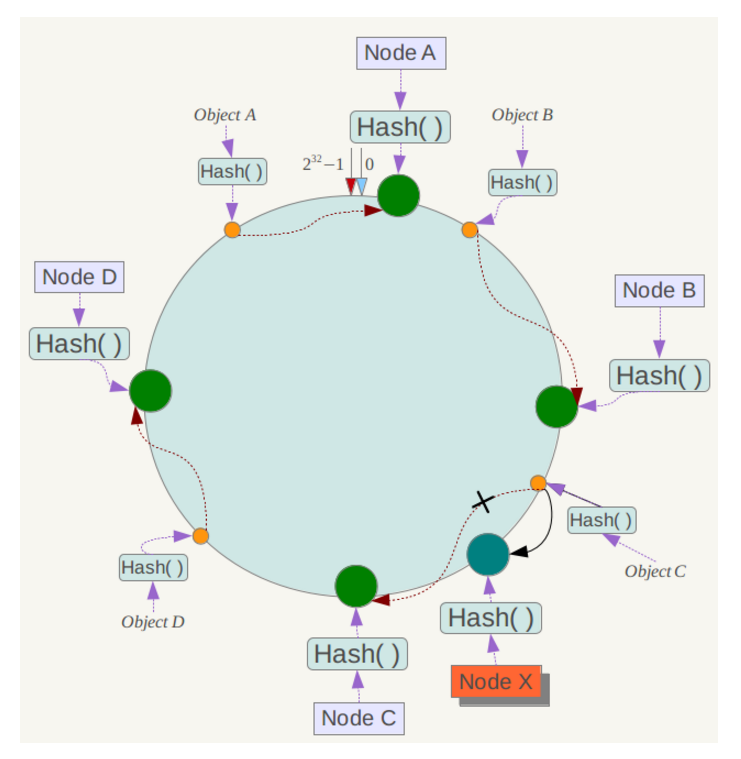
此时对象Object A、B、D不受影响,只有对象C需要重定位到新的Node X 。一般的,在一致性哈希算法中,如果增加一台服务器,则受影响的数据仅仅是新服务器到其环空间中前一台服务器(即沿着逆时针方向行走遇到的第一台服务器)之间数据,其它数据也不会受到影响。
综上所述,一致性哈希算法对于节点的增减都只需重定位环空间中的一小部分数据,具有较好的容错性和可扩展性。
Java代码实现
public class ConsistentHash<T> {
/**
* 节点的复制因子,实际节点个数 * numberOfReplicas = 虚拟节点个数
*/
private final int numberOfReplicas;
/**
* 存储虚拟节点的hash值到真实节点的映射
*/
private final SortedMap<Integer, T> circle = new TreeMap<Integer, T>();
public ConsistentHash(int numberOfReplicas, Collection<T> nodes) {
this.numberOfReplicas = numberOfReplicas;
for (T node : nodes) {
add(node);
}
}
public void add(T node) {
for (int i = 0; i < numberOfReplicas; i++) {
// 对于一个实际机器节点 node, 对应 numberOfReplicas 个虚拟节点
/*
* 不同的虚拟节点(i不同)有不同的hash值,但都对应同一个实际机器node
* 虚拟node一般是均衡分布在环上的,数据存储在顺时针方向的虚拟node上
*/
String nodestr = node.toString() + i;
int hashcode = nodestr.hashCode();
System.out.println("hashcode:" + hashcode);
circle.put(hashcode, node);
}
}
public void remove(T node) {
for (int i = 0; i < numberOfReplicas; i++) {
circle.remove((node.toString() + i).hashCode());
}
}
/**
* 获得一个最近的顺时针节点,根据给定的key 取Hash
* 然后再取得顺时针方向上最近的一个虚拟节点对应的实际节点
* 再从实际节点中取得 数据
*
* @param key
* @return
*/
public T get(Object key) {
if (circle.isEmpty()) {
return null;
}
// node 用String来表示,获得node在哈希环中的hashCode
int hash = key.hashCode();
System.out.println("hashcode----->:" + hash);
//数据映射在两台虚拟机器所在环之间,就需要按顺时针方向寻找机器
if (!circle.containsKey(hash)) {
SortedMap<Integer, T> tailMap = circle.tailMap(hash);
hash = tailMap.isEmpty() ? circle.firstKey() : tailMap.firstKey();
}
return circle.get(hash);
}
public long getSize() {
return circle.size();
}
/**
* 查看表示整个哈希环中各个虚拟节点位置
*/
public void testBalance() {
//获得TreeMap中所有的Key
Set<Integer> sets = circle.keySet();
//将获得的Key集合排序
SortedSet<Integer> sortedSets = new TreeSet<Integer>(sets);
for (Integer hashCode : sortedSets) {
System.out.println(hashCode);
}
System.out.println("----each location 's distance are follows: ----");
/*
* 查看相邻两个hashCode的差值
*/
Iterator<Integer> it = sortedSets.iterator();
Iterator<Integer> it2 = sortedSets.iterator();
if (it2.hasNext()) {
it2.next();
}
long keyPre, keyAfter;
while (it.hasNext() && it2.hasNext()) {
keyPre = it.next();
keyAfter = it2.next();
System.out.println(keyAfter - keyPre);
}
}
public static void main(String[] args) {
Set<String> nodes = new HashSet<String>();
nodes.add("A");
nodes.add("B");
nodes.add("C");
ConsistentHash<String> consistentHash = new ConsistentHash<String>(2, nodes);
consistentHash.add("D");
System.out.println("hash circle size: " + consistentHash.getSize());
System.out.println("location of each node are follows: ");
consistentHash.testBalance();
String node = consistentHash.get("apple");
System.out.println("node----------->:" + node);
}
}


