【DL】——Warmup学习率调整策略_lr poly 学习率原论文

1. warmup的必要性

原理这部分转载自:
神经网络中 warmup 策略为什么有效；有什么理论解释么？

那么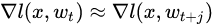在什么时候可能不成立呢？论文[3]告诉我们有两种情况：

• 在训练的开始阶段，模型权重迅速改变
• mini-batch size较小，样本方差较大

第一种情况很好理解，可以认为，刚开始模型对数据的“分布”理解为零，或者是说“均匀分布”（当然这取决于你的初始化）；在第一轮训练的时候，每个数据点对模型来说都是新的，模型会很快地进行数据分布修正，如果这时候学习率就很大，极有可能导致开始的时候就对该数据“过拟合”，后面要通过多轮训练才能拉回来，浪费时间。当训练了一段时间（比如两轮、三轮）后，模型已经对每个数据点看过几遍了，或者说对当前的batch而言有了一些正确的先验，较大的学习率就不那么容易会使模型学偏，所以可以适当调大学习率。这个过程就可以看做是warmup。那么为什么之后还要decay呢？当模型训到一定阶段后（比如十个epoch），模型的分布就已经比较固定了，或者说能学到的新东西就比较少了。如果还沿用较大的学习率，就会破坏这种稳定性，用我们通常的话说，就是已经接近loss的local optimal了，为了靠近这个point，我们就要慢慢来。

第二种情况其实和第一种情况是紧密联系的。在训练的过程中，如果有mini-batch内的数据分布方差特别大，这就会导致模型学习剧烈波动，使其学得的权重很不稳定，这在训练初期最为明显，最后期较为缓解（所以我们要对数据进行scale也是这个道理）。

这说明，在上面两种情况下，我们并不能单纯地成倍增长lr 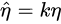。要么改变学习率增长方法，要么设法解决上面两个问题。

前面的两个问题都不是很好解决，于是更多的方法用在了学习率的调整上。

有趣的是，warmup在ResNet[4]中就已经提到了，原文说的是：

We further explore n = 18 that leads to a 110-layer ResNet. In this case, we find that the initial learning rate of 0.1 is slightly too large to start converging . So we use 0.01 to warm up the training until the training error is below 80% (about 400 iterations), and then go back to 0.1 and continue training.

在注释中说的是：

With an initial learning rate of 0.1, it starts converging (<90% error) after several epochs, but still reaches similar accuracy.

这两句话是说，如果一开始就用0.1，虽然最终会收敛，但之后acc还是不会提高（使用了pateaus schedule）；如果用了warmup，在收敛后还能有所提高。也就是说，用warmup和不用warmup达到的收敛点，对之后模型能够达到的suboptimal有影响。这说明什么？这说明不用warmup收敛到的点比用warmup收敛到的点更差。这可以从侧面说明，一开始学偏了的权重后面拉都拉不回来……

从上图(b,c)可以看到，加了warmup增加了模型最后几层的相似性，这表明warmup可以避免FC层的不稳定的剧烈改变。从图一中可以看到，在有了warmup之后，模型能够学得更稳定。综上所述，如果来总结一下现在大batch size和大learning rate下的学习率变化和规律的话，可以认为，学习率是呈现“上升——平稳——下降”的规律，这尤其在深层模型和具有多层MLP层的模型中比较显著。如果从模型学习的角度来说，学习率的这种变化对应了模型“平稳——探索——平稳”的学习阶段。

2. Warmup可视化

说一百道一千直接上代码，可视化一下warmup中学习率随epoch变化的情况。这里直接上代码
Code：

import numpy as np
import matplotlib.pyplot as plt


def Warmup_poly():
    warm_start_lr = 1e-5
    warm_steps = 1000

    lr0 = 1e-2
    nsteps = 2000
    power = 0.9

    lrs = []

    # warmup
    warm_factor = (lr0 / warm_start_lr) ** (1 / warm_steps)
    for i in range(warm_steps):
        warm_lr = warm_start_lr * warm_factor ** i
        lrs.append(warm_lr)

    # poly lr
    for j in range(warm_steps, nsteps):
        lr = lr0 * (1 - (j - warm_steps) / (nsteps - warm_steps)) ** power
        lrs.append(lr)

    lrs = np.array(lrs)
    plt.plot(lrs)
    plt.xlabel("Iters")
    plt.ylabel("lr")
    plt.show()

if __name__ == "__main__":
    Warmup_poly()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

可以看到学习率lr的变化就如前面所说：开始的时候小，而且变换缓慢，后续增大。

2. poly 学习率调整
我们画出整个训练过程中学习率lr的变化，warmup后，我们采用poly学习率的调整方案。学习率的变化公式为：

3. cosine学习率调整
学习率先从很小的数值线性增加到预设学习率，然后按照cos函数值进行衰减，学习率变化在中间比较快，两端变化缓慢。其学习率系数如下图所示。
Code：

def Warmup_cosine():
    warmup_start_lr = 1e-5
    warmup_factor = 1.0069316688
    warmup_steps = 1000

    nsteps = 4000
    base_lr = 0.01
    power = 0.9
    lrs = []
    for i in range(warmup_steps):
        lr = warmup_start_lr * (warmup_factor ** i)             # warm_factor = (base_lr / warmup_start_lr) ** (1 / warmup_steps)
        lrs.append(lr)

    for i in range(warmup_steps, nsteps):
        lr = base_lr * 0.5 * ( math.cos((i - warmup_steps) /(nsteps - warmup_steps) * math.pi) + 1)
        lrs.append(lr)

    
    lrs = np.array(lrs)

    # plot
    plt.plot(lrs)
    plt.xlabel("Iters")
    plt.ylabel("lr")
    plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

reference

1. https://www.zhihu.com/search?type=content&q=warmup
2. https://blog.csdn.net/weixin_42990464/article/details/104640641
3. https://blog.csdn.net/guzhao9901/article/details/114373603