【神经网络与深度学习day10-基于torch使用Lenet实现手写数字识别】_lenet实验

---

5.3 基于LeNet实现手写体数字识别实验

5.3.1 MNIST数据集

5.3.1.1 数据集介绍

手写体数字识别是计算机视觉中最常用的图像分类任务，让计算机识别出给定图片中的手写体数字（0-9共10个数字）。由于手写体风格差异很大，因此手写体数字识别是具有一定难度的任务。

我们采用常用的手写数字识别数据集：MNIST数据集。
我们可以从这里下载手写数字识别数据集：MNIST
MNIST数据集是计算机视觉领域的经典入门数据集，包含了60,000个训练样本和10,000个测试样本。

这些数字已经过尺寸标准化并位于图像中心，图像是固定大小(28×28像素)。

LeNet-5虽然提出的时间比较早，但它是一个非常成功的神经网络模型。

基于LeNet-5的手写数字识别系统在20世纪90年代被美国很多银行使用，用来识别支票上面的手写数字。

导入数据集代码如下：

import json
import gzip
# 打印并观察数据集分布情况
train_set, dev_set, test_set = json.load(gzip.open('./mnist.json.gz'))
train_images, train_labels = train_set[0][:3000], train_set[1][:3000]
dev_images, dev_labels = dev_set[0][:200], dev_set[1][:200]
test_images, test_labels = test_set[0][:200], test_set[1][:200]
train_set, dev_set, test_set = [train_images, train_labels], [dev_images, dev_labels], [test_images, test_labels]
print('Length of train/dev/test set:{}/{}/{}'.format(len(train_set[0]), len(dev_set[0]), len(test_set[0])))
1
2
3
4
5
6
7
8
9

为了方便观察训练过程，我们划分训练集3000张。
Length of train/dev/test set:3000/200/200

数据集第一张图片展示：
代码：

import numpy as np
import matplotlib.pyplot as plt
import torch
import PIL.Image as Image
image, label = train_set[0][0], train_set[1][0]
image, label = np.array(image).astype('float32'), int(label)
# 原始图像数据为长度784的行向量，需要调整为[28,28]大小的图像
image = np.reshape(image, [28,28])
image = Image.fromarray(image.astype('uint8'), mode='L')
print("The number in the picture is {}".format(label))
plt.figure(figsize=(5, 5))
plt.imshow(image)
plt.savefig('conv-number5.pdf')
1
2
3
4
5
6
7
8
9
10
11
12
13

5.3.1.2 数据集导入

import torchvision.transforms as transforms

# 数据预处理
transforms = transforms.Compose([transforms.Resize(32),transforms.ToTensor(), transforms.Normalize(mean=[0.5], std=[0.5])])
import random
from torch.utils.data import Dataset,DataLoader

class MNIST_dataset(Dataset):
    def __init__(self, dataset, transforms, mode='train'):
        self.mode = mode
        self.transforms =transforms
        self.dataset = dataset

    def __getitem__(self, idx):
        # 获取图像和标签
        image, label = self.dataset[0][idx], self.dataset[1][idx]
        image, label = np.array(image).astype('float32'), int(label)
        image = np.reshape(image, [28,28])
        image = Image.fromarray(image.astype('uint8'), mode='L')
        image = self.transforms(image)

        return image, label

    def __len__(self):
        return len(self.dataset[0])
# 加载 mnist 数据集
train_dataset = MNIST_dataset(dataset=train_set, transforms=transforms, mode='train')
test_dataset = MNIST_dataset(dataset=test_set, transforms=transforms, mode='test')
dev_dataset = MNIST_dataset(dataset=dev_set, transforms=transforms, mode='dev')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

5.3.2 模型构建

这里的LeNet-5和原始版本有4点不同：

1. C3层没有使用连接表来减少卷积数量。
2. 汇聚层使用了简单的平均汇聚，没有引入权重和偏置参数以及非线性激活函数。
3. 卷积层的激活函数使用ReLU函数。
4. 最后的输出层为一个全连接线性层。

网络共有7层，包含3个卷积层、2个汇聚层以及2个全连接层的简单卷积神经网络接，受输入图像大小为32×32=1024，输出对应10个类别的得分。

5.3.2.1 使用自定义算子，构建LeNet-5模型

自定义的Conv2D和Pool2D算子中包含多个for循环，所以运算速度比较慢。

import torch.nn.functional as F
import torch.nn as nn


class Model_LeNet(nn.Module):
    def __init__(self, in_channels, num_classes=10):
        super(Model_LeNet, self).__init__()
        # 卷积层：输出通道数为6，卷积核大小为5×5
        self.conv1 = nn.Conv2d(in_channels=in_channels, out_channels=6, kernel_size=5)
        # 汇聚层：汇聚窗口为2×2，步长为2
        self.pool2 = nn.MaxPool2d(kernel_size=(2, 2), stride=2)
        # 卷积层：输入通道数为6，输出通道数为16，卷积核大小为5×5，步长为1
        self.conv3 = nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5, stride=1)
        # 汇聚层：汇聚窗口为2×2，步长为2
        self.pool4 = nn.AvgPool2d(kernel_size=(2, 2), stride=2)
        # 卷积层：输入通道数为16，输出通道数为120，卷积核大小为5×5
        self.conv5 = nn.Conv2d(in_channels=16, out_channels=120, kernel_size=5, stride=1)
        # 全连接层：输入神经元为120，输出神经元为84
        self.linear6 = nn.Linear(120, 84)
        # 全连接层：输入神经元为84，输出神经元为类别数
        self.linear7 = nn.Linear(84, num_classes)

    def forward(self, x):
        # C1：卷积层+激活函数

        output = F.relu(self.conv1(x))
        # S2：汇聚层
        output = self.pool2(output)
        # C3：卷积层+激活函数
        output = F.relu(self.conv3(output))
        # S4：汇聚层
        output = self.pool4(output)
        # C5：卷积层+激活函数
        output = F.relu(self.conv5(output))
        # 输入层将数据拉平[B,C,H,W] -> [B,CxHxW]
        output = torch.squeeze(output, dim=3)
        output = torch.squeeze(output, dim=2)
        # F6：全连接层
        output = F.relu(self.linear6(output))
        # F7：全连接层
        output = self.linear7(output)
        return output

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

5.3.2.2 使用pytorch中的相应算子，构建LeNet-5模型

torch.nn.Conv2d()；torch.nn.MaxPool2d()；torch.nn.avg_pool2d()

class Torch_LeNet(nn.Module):
    def __init__(self, in_channels, num_classes=10):
        super(Torch_LeNet, self).__init__()
        # 卷积层：输出通道数为6，卷积核大小为5*5
        self.conv1 = nn.Conv2d(in_channels=in_channels, out_channels=6, kernel_size=5)
        # 汇聚层：汇聚窗口为2*2，步长为2
        self.pool2 = nn.MaxPool2d(kernel_size=2, stride=2)
        # 卷积层：输入通道数为6，输出通道数为16，卷积核大小为5*5
        self.conv3 = nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5)
        # 汇聚层：汇聚窗口为2*2，步长为2
        self.pool4 = nn.AvgPool2d(kernel_size=2, stride=2)
        # 卷积层：输入通道数为16，输出通道数为120，卷积核大小为5*5
        self.conv5 = nn.Conv2d(in_channels=16, out_channels=120, kernel_size=5)
        # 全连接层：输入神经元为120，输出神经元为84
        self.linear6 = nn.Linear(in_features=120, out_features=84)
        # 全连接层：输入神经元为84，输出神经元为类别数
        self.linear7 = nn.Linear(in_features=84, out_features=num_classes)

    def forward(self, x):
        # C1：卷积层+激活函数
        output = F.relu(self.conv1(x))
        # S2：汇聚层
        output = self.pool2(output)
        # C3：卷积层+激活函数
        output = F.relu(self.conv3(output))
        # S4：汇聚层
        output = self.pool4(output)
        # C5：卷积层+激活函数
        output = F.relu(self.conv5(output))
        # 输入层将数据拉平[B,C,H,W] -> [B,CxHxW]
        output = torch.squeeze(output, dim=3)
        output = torch.squeeze(output, dim=2)
        # F6：全连接层
        output = F.relu(self.linear6(output))
        # F7：全连接层
        output = self.linear7(output)
        return output
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

5.3.2.3模型测试

测试LeNet-5模型，构造一个形状为 [1,1,32,32]的输入数据送入网络，观察每一层特征图的形状变化。

# 这里用np.random创建一个随机数组作为输入数据
inputs = np.random.randn(*[1, 1, 32, 32])
inputs = inputs.astype('float32')

# 创建Model_LeNet类的实例，指定模型名称和分类的类别数目
model = Model_LeNet(in_channels=1, num_classes=10)
print(model)
# 通过调用LeNet从基类继承的sublayers()函数，查看LeNet中所包含的子层
print(model.named_parameters())
x = torch.tensor(inputs)
print(x)
for item in model.children():
    # item是LeNet类中的一个子层
    # 查看经过子层之后的输出数据形状
    item_shapex = 0
    names = []
    parameter = []
    for name in item.named_parameters():
        names.append(name[0])
        parameter.append(name[1])
        item_shapex += 1
    try:
        x = item(x)
    except:
        # 如果是最后一个卷积层输出，需要展平后才可以送入全连接层
        x = x.reshape([x.shape[0], -1])
        x = item(x)

    if item_shapex == 2:
        # 查看卷积和全连接层的数据和参数的形状，
        # 其中item.parameters()[0]是权重参数w，item.parameters()[1]是偏置参数b
        print(item, x.shape, parameter[0].shape, parameter[1].shape)
    else:
        # 汇聚层没有参数
        print(item, x.shape)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

结果：

5.3.2.4 测试两个网络的运算速度。

测试两个网络的运算速度的代码如下：

import time

# 这里用np.random创建一个随机数组作为测试数据
inputs = np.random.randn(*[1,1,32,32])
inputs = inputs.astype('float32')
x = torch.tensor(inputs)

# 创建Model_LeNet类的实例，指定模型名称和分类的类别数目
model = Model_LeNet(in_channels=1, num_classes=10)
# 创建Torch_LeNet类的实例，指定模型名称和分类的类别数目
torch_model = Torch_LeNet(in_channels=1, num_classes=10)

# 计算Model_LeNet类的运算速度
model_time = 0
for i in range(60):
    strat_time = time.time()
    out = model(x)
    end_time = time.time()
    # 预热10次运算，不计入最终速度统计
    if i < 10:
        continue
    model_time += (end_time - strat_time)
avg_model_time = model_time / 50
print('Model_LeNet speed:', avg_model_time, 's')
# 计算Torch_LeNet类的运算速度
torch_model_time = 0
for i in range(60):
    strat_time = time.time()
    torch_out = torch_model(x)
    end_time = time.time()
    # 预热10次运算，不计入最终速度统计
    if i < 10:
        continue
    torch_model_time += (end_time - strat_time)
avg_torch_model_time = torch_model_time / 50

print('Torch_LeNet speed:', avg_torch_model_time, 's')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

测试结果：

我们发现，自定义算子慢于torch算子，但是相差也不算很大，可以忽略不计，但是torch的性能表现确实比自定义算子的性能表现要好。

5.3.2.5 测试两个网络的运算结果

令两个网络加载同样的权重，测试一下两个网络的输出结果是否一致。

# 这里用np.random创建一个随机数组作为测试数据
inputs = np.random.randn(*[1,1,32,32])
inputs = inputs.astype('float32')
x = torch.tensor(inputs)

# 创建Model_LeNet类的实例，指定模型名称和分类的类别数目
model = Model_LeNet(in_channels=1, num_classes=10)
# 获取网络的权重
params = model.state_dict()
# 自定义Conv2D算子的bias参数形状为[out_channels, 1]
# torch API中Conv2D算子的bias参数形状为[out_channels]
# 需要进行调整后才可以赋值
for key in params:
    if 'bias' in key:
        params[key] = params[key].squeeze()
# 创建Torch_LeNet类的实例，指定模型名称和分类的类别数目
torch_model = Torch_LeNet(in_channels=1, num_classes=10)
# 将Model_LeNet的权重参数赋予给Torch_LeNet模型，保持两者一致
torch_model.load_state_dict(params)

# 打印结果保留小数点后6位
torch.set_printoptions(6)
# 计算Model_LeNet的结果
output = model(x)
print('Model_LeNet output: ', output)
# 计算Torch_LeNet的结果
torch_output = torch_model(x)
print('Torch_LeNet output: ', torch_output)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

运算结果比较：

5.3.2.6 统计LeNet-5模型的参数量和计算量。

我们使用torchsummary统计参数量和计算量：
代码如下：

from torchsummary import summary
model = Torch_LeNet(in_channels=1, num_classes=10)
params_info = summary(model, (1, 32, 32))
print(params_info)
1
2
3
4

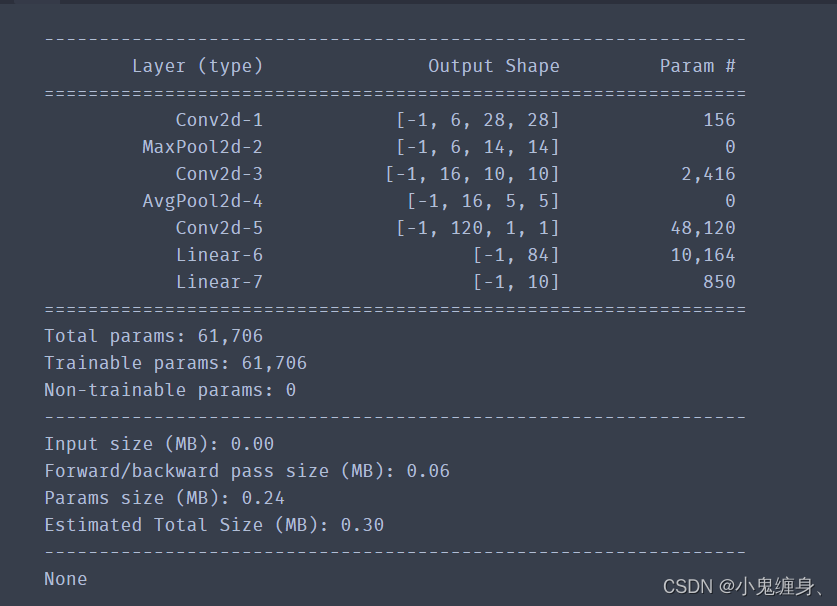
5.3.2.7 paddle可以统计Floats,torch可以吗？

在飞桨中，还可以使用paddle.flopsAPI自动统计计算量。pytorch可以么？
回答：可以，在torch中，我们可以使用torchstat统计计算量。

from torchstat import stat
# 导入模型，输入一张输入图片的尺寸
stat(model, (1, 32,32))
1
2
3

结果展示：

5.3.3 模型训练

使用交叉熵损失函数，并用随机梯度下降法作为优化器来训练LeNet-5网络。
用RunnerV3在训练集上训练5个epoch，并保存准确率最高的模型作为最佳模型。
我们选择训练6个epoch，然后给出RunnerV3和Accuracy的code:

class RunnerV3(object):
    def __init__(self, model, optimizer, loss_fn, metric, **kwargs):
        self.model = model
        self.optimizer = optimizer
        self.loss_fn = loss_fn
        self.metric = metric  # 只用于计算评价指标

        # 记录训练过程中的评价指标变化情况
        self.dev_scores = []

        # 记录训练过程中的损失函数变化情况
        self.train_epoch_losses = []  # 一个epoch记录一次loss
        self.train_step_losses = []  # 一个step记录一次loss
        self.dev_losses = []

        # 记录全局最优指标
        self.best_score = 0

    def train(self, train_loader, dev_loader=None, **kwargs):
        # 将模型切换为训练模式
        self.model.train()

        # 传入训练轮数，如果没有传入值则默认为0
        num_epochs = kwargs.get("num_epochs", 0)
        # 传入log打印频率，如果没有传入值则默认为100
        log_steps = kwargs.get("log_steps", 100)
        # 评价频率
        eval_steps = kwargs.get("eval_steps", 0)

        # 传入模型保存路径，如果没有传入值则默认为"best_model.pdparams"
        save_path = kwargs.get("save_path", "best_model.pdparams")

        custom_print_log = kwargs.get("custom_print_log", None)

        # 训练总的步数
        num_training_steps = num_epochs * len(train_loader)

        if eval_steps:
            if self.metric is None:
                raise RuntimeError('Error: Metric can not be None!')
            if dev_loader is None:
                raise RuntimeError('Error: dev_loader can not be None!')

        # 运行的step数目
        global_step = 0

        # 进行num_epochs轮训练
        for epoch in range(num_epochs):
            # 用于统计训练集的损失
            total_loss = 0
            for step, data in enumerate(train_loader):
                X, y = data
                # 获取模型预测
                logits = self.model(X)
                loss = self.loss_fn(logits, y)  # 默认求mean
                total_loss += loss

                # 训练过程中，每个step的loss进行保存
                self.train_step_losses.append((global_step, loss.item()))

                if log_steps and global_step % log_steps == 0:
                    print(
                        f"[Train] epoch: {epoch}/{num_epochs}, step: {global_step}/{num_training_steps}, loss: {loss.item():.5f}")

                # 梯度反向传播，计算每个参数的梯度值
                loss.backward()

                if custom_print_log:
                    custom_print_log(self)

                # 小批量梯度下降进行参数更新
                self.optimizer.step()
                # 梯度归零
                optimizer.zero_grad()

                # 判断是否需要评价
                if eval_steps > 0 and global_step > 0 and \
                        (global_step % eval_steps == 0 or global_step == (num_training_steps - 1)):

                    dev_score, dev_loss = self.evaluate(dev_loader, global_step=global_step)
                    print(f"[Evaluate]  dev score: {dev_score:.5f}, dev loss: {dev_loss:.5f}")

                    # 将模型切换为训练模式
                    self.model.train()

                    # 如果当前指标为最优指标，保存该模型
                    if dev_score > self.best_score:
                        self.save_model(save_path)
                        print(
                            f"[Evaluate] best accuracy performence has been updated: {self.best_score:.5f} --> {dev_score:.5f}")
                        self.best_score = dev_score

                global_step += 1

            # 当前epoch 训练loss累计值
            trn_loss = (total_loss / len(train_loader)).item()
            # epoch粒度的训练loss保存
            self.train_epoch_losses.append(trn_loss)

        print("[Train] Training done!")

    # 模型评估阶段，使用'paddle.no_grad()'控制不计算和存储梯度
    @torch.no_grad()
    def evaluate(self, dev_loader, **kwargs):
        assert self.metric is not None

        # 将模型设置为评估模式
        self.model.eval()

        global_step = kwargs.get("global_step", -1)

        # 用于统计训练集的损失
        total_loss = 0

        # 重置评价
        self.metric.reset()

        # 遍历验证集每个批次
        for batch_id, data in enumerate(dev_loader):
            X, y = data

            # 计算模型输出
            logits = self.model(X)

            # 计算损失函数
            loss = self.loss_fn(logits, y).item()
            # 累积损失
            total_loss += loss

            # 累积评价
            self.metric.update(logits, y)

        dev_loss = (total_loss / len(dev_loader))
        dev_score = self.metric.accumulate()

        # 记录验证集loss
        if global_step != -1:
            self.dev_losses.append((global_step, dev_loss))
            self.dev_scores.append(dev_score)

        return dev_score, dev_loss

    # 模型评估阶段，使用'paddle.no_grad()'控制不计算和存储梯度
    @torch.no_grad()
    def predict(self, x, **kwargs):
        # 将模型设置为评估模式
        self.model.eval()
        # 运行模型前向计算，得到预测值
        logits = self.model(x)
        return logits

    def save_model(self, save_path):
        torch.save(self.model.state_dict(), save_path)

    def load_model(self, model_path):
        state_dict = torch.load(model_path)
        self.model.load_state_dict(state_dict)
import torch
#新增准确率计算函数
def accuracy(preds, labels):
    """
    输入：
        - preds：预测值，二分类时，shape=[N, 1]，N为样本数量，多分类时，shape=[N, C]，C为类别数量
        - labels：真实标签，shape=[N, 1]
    输出：
        - 准确率：shape=[1]
    """
    print(preds)
    # 判断是二分类任务还是多分类任务，preds.shape[1]=1时为二分类任务，preds.shape[1]>1时为多分类任务
    if preds.shape[1] == 1:
        # 二分类时，判断每个概率值是否大于0.5，当大于0.5时，类别为1，否则类别为0
        # 使用'torch.can_cast'将preds的数据类型转换为float32类型
        preds = torch.can_cast((preds>=0.5).dtype,to=torch.float32)
    else:
        # 多分类时，使用'torch.argmax'计算最大元素索引作为类别
        preds = torch.argmax(preds,dim=1)
        torch.can_cast(preds.dtype,torch.int32)
    return torch.mean(torch.tensor((preds == labels), dtype=torch.float32))


class Accuracy():
    def __init__(self):
        """
        输入：
           - is_logist: outputs是logist还是激活后的值
        """

        # 用于统计正确的样本个数
        self.num_correct = 0
        # 用于统计样本的总数
        self.num_count = 0

        self.is_logist = True

    def update(self, outputs, labels):
        """
        输入：
           - outputs: 预测值, shape=[N,class_num]
           - labels: 标签值, shape=[N,1]
        """

        # 判断是二分类任务还是多分类任务，shape[1]=1时为二分类任务，shape[1]>1时为多分类任务
        if outputs.shape[1] == 1: # 二分类
            outputs = torch.squeeze(outputs, axis=-1)
            if self.is_logist:
                # logist判断是否大于0
                preds = torch.can_cast((outputs>=0), dtype=torch.float32)
            else:
                # 如果不是logist，判断每个概率值是否大于0.5，当大于0.5时，类别为1，否则类别为0
                preds = torch.can_cast((outputs>=0.5), dtype=torch.float32)
        else:
            # 多分类时，使用'paddle.argmax'计算最大元素索引作为类别
            preds = torch.argmax(outputs, dim=1).int()

        # 获取本批数据中预测正确的样本个数
        labels = torch.squeeze(labels, dim=-1)
        batch_correct = torch.sum(torch.tensor(preds == labels, dtype=torch.float32)).numpy()
        batch_count = len(labels)

        # 更新num_correct 和 num_count
        self.num_correct += batch_correct
        self.num_count += batch_count

    def accumulate(self):
        # 使用累计的数据，计算总的指标
        if self.num_count == 0:
            return 0
        return self.num_correct / self.num_count

    def reset(self):
        # 重置正确的数目和总数
        self.num_correct = 0
        self.num_count = 0

    def name(self):
        return "Accuracy"
import torch.optim as opti
# 学习率大小
lr = 0.1
# 批次大小
batch_size = 64
# 加载数据
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
dev_loader = DataLoader(dev_dataset, batch_size=batch_size)
test_loader = DataLoader(test_dataset, batch_size=batch_size)
# 定义LeNet网络
# 自定义算子实现的LeNet-5
model = Model_LeNet(in_channels=1, num_classes=10)
# 飞桨API实现的LeNet-5
# model = Paddle_LeNet(in_channels=1, num_classes=10)
# 定义优化器
optimizer = opti.SGD(model.parameters(), 0.2)
# 定义损失函数
loss_fn = F.cross_entropy
# 定义评价指标
metric = Accuracy()
# 实例化 RunnerV3 类，并传入训练配置。
runner = RunnerV3(model, optimizer, loss_fn, metric)
# 启动训练
log_steps = 15
eval_steps = 15
runner.train(train_loader, dev_loader, num_epochs=6, log_steps=log_steps,
                eval_steps=eval_steps, save_path="best_model.pdparams")

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264

结果展示：
[Train] epoch: 0/6, step: 0/282, loss: 2.29864
[Train] epoch: 0/6, step: 15/282, loss: 2.23512
[Evaluate] dev score: 0.35000, dev loss: 2.22403
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.35000
:60: UserWarning: To copy construct from a tensor, it is recommended to use sourceTensor.clone().detach() or sourceTensor.clone().detach().requires_grad_(True), rather than torch.tensor(sourceTensor).
batch_correct = torch.sum(torch.tensor(preds == labels, dtype=torch.float32)).numpy()
[Train] epoch: 0/6, step: 30/282, loss: 2.26119
[Evaluate] dev score: 0.09000, dev loss: 2.31535
[Train] epoch: 0/6, step: 45/282, loss: 1.87482
[Evaluate] dev score: 0.31500, dev loss: 1.96644
[Train] epoch: 1/6, step: 60/282, loss: 1.49791
[Evaluate] dev score: 0.32500, dev loss: 1.90903
[Train] epoch: 1/6, step: 75/282, loss: 1.08951
[Evaluate] dev score: 0.43000, dev loss: 1.97639
[Evaluate] best accuracy performence has been updated: 0.35000 --> 0.43000
[Train] epoch: 1/6, step: 90/282, loss: 0.72709
[Evaluate] dev score: 0.72000, dev loss: 0.62929
[Evaluate] best accuracy performence has been updated: 0.43000 --> 0.72000
[Train] epoch: 2/6, step: 105/282, loss: 1.01030
[Evaluate] dev score: 0.58000, dev loss: 1.11268
[Train] epoch: 2/6, step: 120/282, loss: 0.30258
[Evaluate] dev score: 0.84000, dev loss: 0.36762
[Evaluate] best accuracy performence has been updated: 0.72000 --> 0.84000
[Train] epoch: 2/6, step: 135/282, loss: 0.27759
[Evaluate] dev score: 0.87500, dev loss: 0.38257
[Evaluate] best accuracy performence has been updated: 0.84000 --> 0.87500
[Train] epoch: 3/6, step: 150/282, loss: 0.37689
[Evaluate] dev score: 0.81500, dev loss: 0.50451
[Train] epoch: 3/6, step: 165/282, loss: 0.39598
[Evaluate] dev score: 0.90500, dev loss: 0.26139
[Evaluate] best accuracy performence has been updated: 0.87500 --> 0.90500
[Train] epoch: 3/6, step: 180/282, loss: 0.20255
[Evaluate] dev score: 0.89500, dev loss: 0.26024
[Train] epoch: 4/6, step: 195/282, loss: 0.08575
[Evaluate] dev score: 0.92000, dev loss: 0.16601
[Evaluate] best accuracy performence has been updated: 0.90500 --> 0.92000
[Train] epoch: 4/6, step: 210/282, loss: 0.16293
[Evaluate] dev score: 0.95000, dev loss: 0.14370
[Evaluate] best accuracy performence has been updated: 0.92000 --> 0.95000
[Train] epoch: 4/6, step: 225/282, loss: 0.20410
[Evaluate] dev score: 0.95000, dev loss: 0.14841
[Train] epoch: 5/6, step: 240/282, loss: 0.09400
[Evaluate] dev score: 0.94000, dev loss: 0.15105
[Train] epoch: 5/6, step: 255/282, loss: 0.30644
[Evaluate] dev score: 0.96000, dev loss: 0.17032
[Evaluate] best accuracy performence has been updated: 0.95000 --> 0.96000
[Train] epoch: 5/6, step: 270/282, loss: 0.20965
[Evaluate] dev score: 0.87500, dev loss: 0.31949
[Evaluate] dev score: 0.94000, dev loss: 0.12479
[Train] Training done!

可以看出的是，最好的精确度performence展示已经达到了96%，在验证集上的准确度也达到了94%，取得了不错的效果。

5.3.4 模型评价

我们看一下训练过程中的误差变化和精确率变化：

#可视化误差
def plot(runner, fig_name):
    plt.figure(figsize=(10,5))

    plt.subplot(1,2,1)
    train_items = runner.train_step_losses[::30]
    train_steps=[x[0] for x in train_items]
    train_losses = [x[1] for x in train_items]

    plt.plot(train_steps, train_losses, color='#8E004D', label="Train loss")
    if runner.dev_losses[0][0]!=-1:
        dev_steps=[x[0] for x in runner.dev_losses]
        dev_losses = [x[1] for x in runner.dev_losses]
        plt.plot(dev_steps, dev_losses, color='#E20079', linestyle='--', label="Dev loss")
    #绘制坐标轴和图例
    plt.ylabel("loss", fontsize='x-large')
    plt.xlabel("step", fontsize='x-large')
    plt.legend(loc='upper right', fontsize='x-large')
    
    plt.subplot(1,2,2)
    #绘制评价准确率变化曲线
    if runner.dev_losses[0][0]!=-1:
        plt.plot(dev_steps, runner.dev_scores, 
            color='#E20079', linestyle="--", label="Dev accuracy")
    else:
        plt.plot(list(range(len(runner.dev_scores))), runner.dev_scores, 
            color='#E20079', linestyle="--", label="Dev accuracy")
    #绘制坐标轴和图例
    plt.ylabel("score", fontsize='x-large')
    plt.xlabel("step", fontsize='x-large')
    plt.legend(loc='lower right', fontsize='x-large')
    
    plt.savefig(fig_name)
    plt.show()
runner.load_model('best_model.pdparams')
plot(runner, 'cnn-loss1.pdf')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

可视化结果：

测试准确率：

# 加载最优模型
runner.load_model('best_model.pdparams')
# 模型评价
score, loss = runner.evaluate(test_loader)
print("[Test] accuracy/loss: {:.4f}/{:.4f}".format(score, loss))
1
2
3
4
5

5.3.5 模型预测

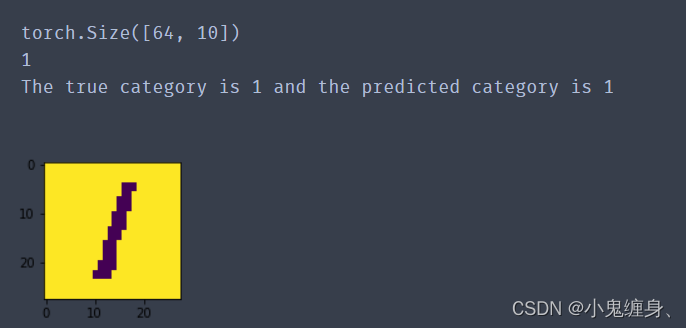
# 获取测试集中第一条数
X, label = next(iter(test_loader))
logits = runner.predict(X)
# 多分类，使用softmax计算预测概率
pred = F.softmax(logits,dim=1)
print(pred.shape)
# 获取概率最大的类别
pred_class = torch.argmax(pred[2]).numpy()
print(pred_class)
label = label[2].numpy()
# 输出真实类别与预测类别
print("The true category is {} and the predicted category is {}".format(label, pred_class))
# 可视化图片
plt.figure(figsize=(2, 2))
image, label = test_set[0][2], test_set[1][2]
image= np.array(image).astype('float32')
image = np.reshape(image, [28,28])
image = Image.fromarray(image.astype('uint8'), mode='L')
plt.imshow(image)
plt.savefig('cnn-number2.pdf')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

实现结果：

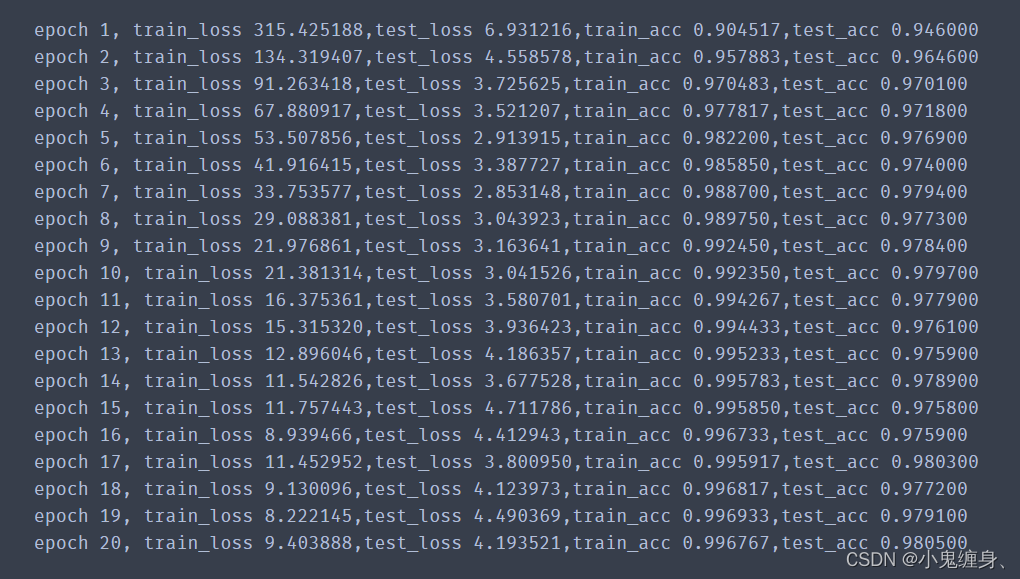
使用前馈神经网络实现MNIST识别，与LeNet效果对比。（选做）

使用前馈神经网络实现MNIST识别代码：

from torchvision import datasets,transforms
from torch.utils.data import DataLoader
import matplotlib.pyplot as plt
import torchvision
from torch import nn
import numpy as np
import torch
transformation =transforms.Compose([
    transforms.ToTensor()  #转换到Tensor，并且转换为0-1之间,将channel 放到第一个纬度
])
train_ds = datasets.MNIST('data/',train = True,transform = transformation,download = True)
test_ds = datasets.MNIST('data/',train = False,transform = transformation,download = True)
# len(train_ds)
# len(test_ds)
train_loader = DataLoader(train_ds,batch_size =64 ,shuffle = True,num_workers = 16)
test_loader = DataLoader(test_ds,batch_size =256 ,shuffle = False,num_workers = 16)
class Model(nn.Module):
    def __init__(self):
        super().__init__()
        self.linear1 = nn.Linear(28*28,128)
        self.linear2 = nn.Linear(128,64)
        self.linear3 = nn.Linear(64,10)
    def forward(self,input):
        x = input.view(-1,28*28)
        x = nn.functional.relu(self.linear1(x))
        x = nn.functional.relu(self.linear2(x))
        y = self.linear3(x)
        return y
model = Model()
loss_fn  = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(),lr=0.001)
def accuracy(y_pred,y_true):
    y_pred = torch.argmax(y_pred,dim=1)
    acc = (y_pred==y_true).float().mean()
    return acc
#测试集
def evaluate_testset(data_loader,model):
    acc_sum,loss_sum,total_example = 0.0,0.0,0
    for x,y in data_loader:
        y_hat = model(x)
        acc_sum += (y_hat.argmax(dim=1)==y).sum().item()
        loss = loss_fn(y_hat,y) 
        loss_sum += loss.item()
        total_example+=y.shape[0]
    return acc_sum/total_example,loss_sum
#定义模型训练函数
def train(model,train_loader,test_loader,loss,num_epochs,batch_size,params=None,lr=None,optimizer=None):
    train_ls = []
    test_ls = []
    for epoch in range(num_epochs): # 训练模型一共需要num_epochs个迭代周期
        train_loss_sum, train_acc_num,total_examples = 0.0,0.0,0
        for x, y in train_loader: # x和y分别是小批量样本的特征和标签
            y_pred = model(x)
            loss = loss_fn(y_pred, y)  #计算损失
            optimizer.zero_grad() # 梯度清零
            loss.backward()  # 反向传播
            optimizer.step() #梯度更新
            total_examples += y.shape[0]
            train_loss_sum += loss.item()
            train_acc_num += (y_pred.argmax(dim=1)==y).sum().item()
        train_ls.append(train_loss_sum)
        test_acc,test_loss = evaluate_testset(test_loader,model)
        test_ls.append(test_loss)
        print('epoch %d, train_loss %.6f,test_loss %f,train_acc %.6f,test_acc %.6f'%(epoch+1, train_ls[epoch],test_ls[epoch],train_acc_num/total_examples,test_acc))
    return
num_epoch  = 20
batch_size = 64
train(model,train_loader,test_loader,loss_fn,num_epoch,batch_size,params=model.parameters,lr=0.001,optimizer=optimizer)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69

训练结果示意：

参数量的对比：

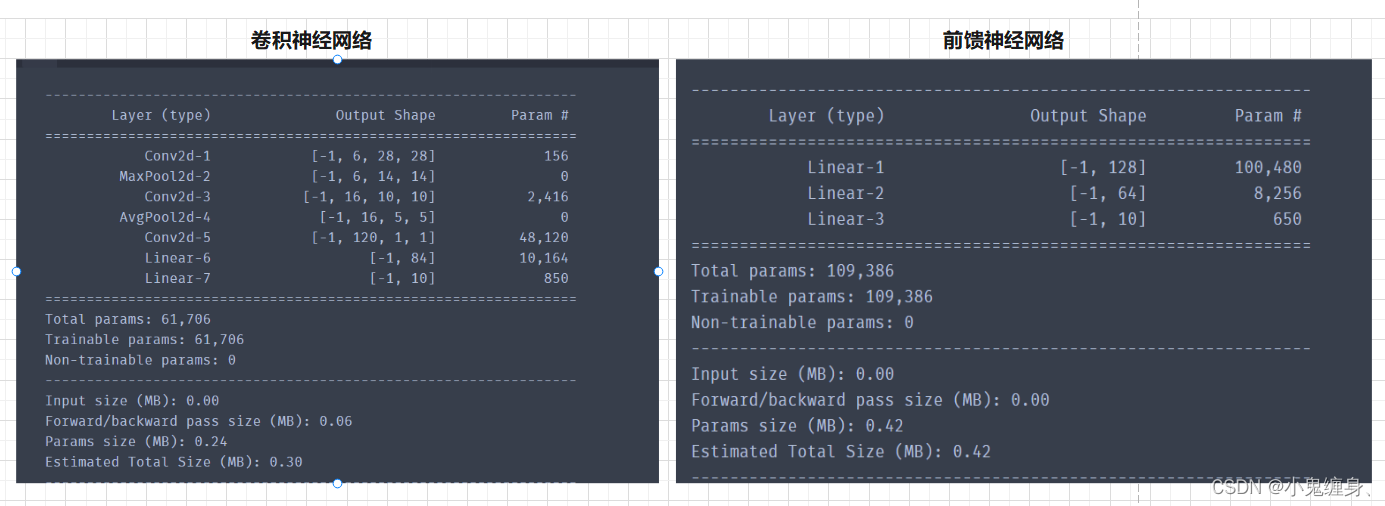
对比结果发现，卷积神经网络的参数量只有6w，而前馈神经网络却有10w+的参数量，虽然前馈神经网络展现的性能比卷积神经网络好（也可能是因为我卷积神经网络的训练次数太少，具体再高的准确率大家可以自己尝试对比一下），但其5%的准确率却需要再加一倍的性能，这显然展现了卷积神经网络的优点，下面我们来对比一下浮点运算数：

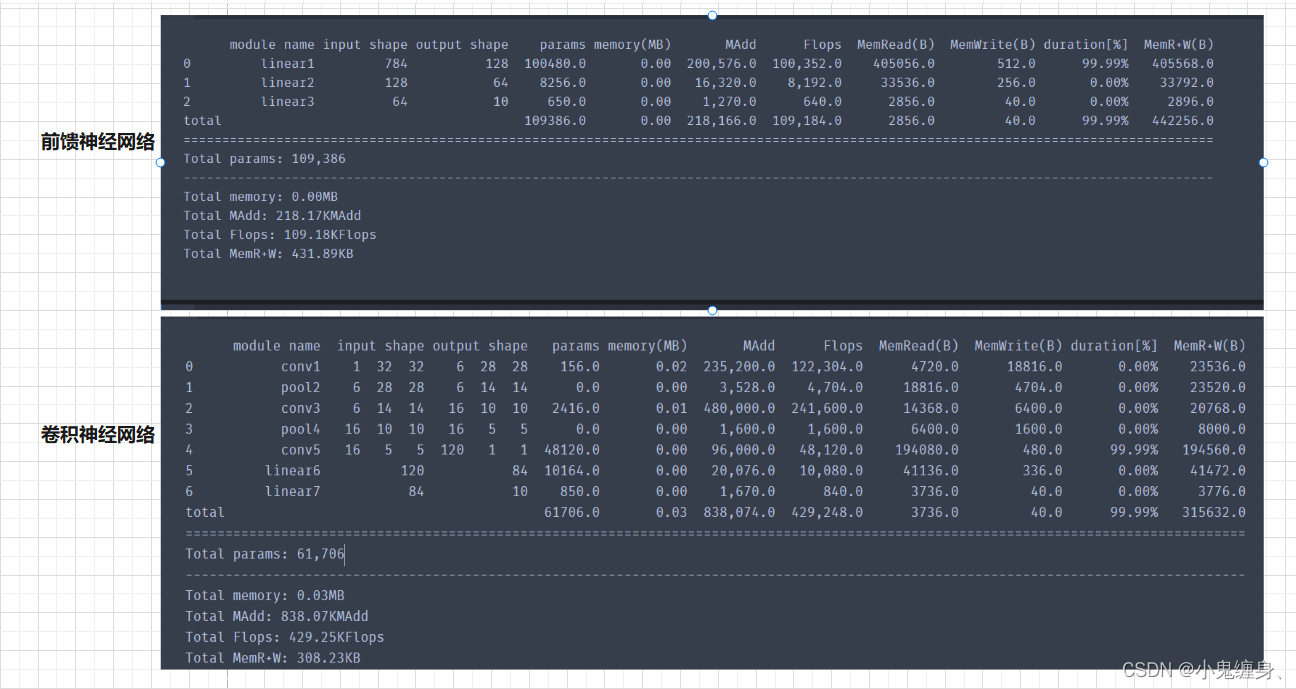
我们得到的结果是卷积神经网络的计算量>前馈神经网络的计算量，但是为什么会这样呢？我查找了很多资料，各大博客和视频，没有找到具体相关的解释，我的理解是虽然卷积神经网络的参数量少于亲前馈神经网络，但是由于其层数的增多，导致计算量不可避免的增加，但是同等性能下，卷积神经网络肯定是优于前馈神经网络的。

可视化LeNet中的部分特征图和卷积核，谈谈自己的看法。（选做）

C1：卷积层+激活函数

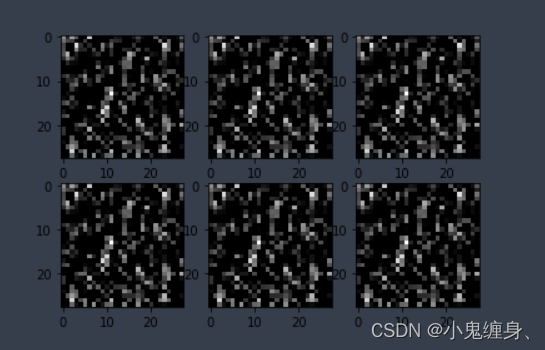
S2：汇聚层

C3：卷积层+激活函数

S4：汇聚层

---

总结

今天基于torch使用Lenet实现手写数字识别，实验也写了好久，也和别人探讨了一些准确率低的问题所在，在只更改邱老师的paddle代码的时候，经常会出来准确率为10%的问题，也就是10张图片瞎猜一张的准确率，如下图：

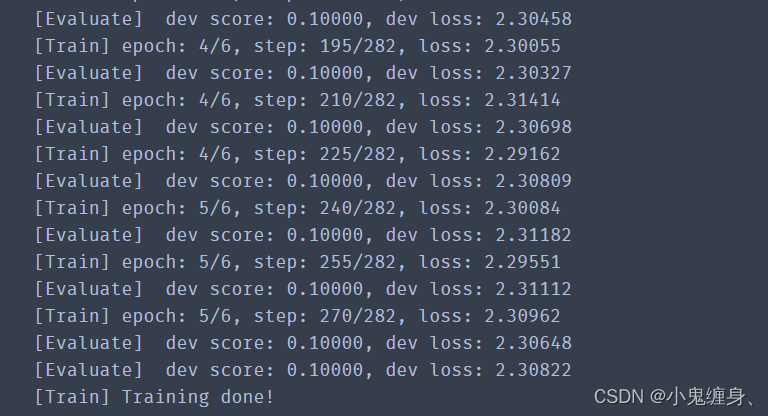
在探讨问题的过程中，一开始我认为是学习率的影响因素，将学习率设置为0.1、0.2、1、2、5、10、20等发现准确率只提高了5个百分点，甚至只提升一个百分点，和别人探讨的过程中，我们发现在torch中，transform.Normalize的参数过大，Normalize是对数据做标准化处理的，如果参数设置为175.5和175.5的话，会导致均值处在175.5，方差在175.5内，由于我们使用的图片在transforms.ToTensor处理后，值均位于0-1之间，这就解释了为什么这个参数对于卷积神经网络的结果影响之大，顺便提一句，在Normalize中，均值反映了图像的亮度，均值越大说明图像亮度越大，反之越小；标准差反映了图像像素值与均值的离散程度，标准差越大说明图像的质量越好； 我们重新修改为mean = 0.5 和std = 0.5 才得到了这个94%的准确率，至于为什么没有到99%，大家可以自己尝试学习率的更改，我这里得到了一个差不多的准确率就没再调参，大家想要得到99%的准确率可以调这个代码的lr试一下，在这里哦~(模型训练5.3.3这一行，我设置的是0.2)：

这就是今天的全部内容了。

Rerferences:

前馈神经网络实现手写数字识别
transforms.Normalize，计算数据量大数据集的像素均值（mean)和标准差（std)
NNDL 实验5（上）
卷积神经网络 — 动手学深度学习 2.0.0-beta1 documentation (d2l.ai)
老师博客：
NNDL 实验六 卷积神经网络（3）LeNet实现MNIST