devbox
小丑西瓜9
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

【数据结构】集合与散列表

作者：小丑西瓜9 | 2024-05-13 00:51:25

赞

踩

【数据结构】集合与散列表

文章目录

集合中的数据元素除属于同一个集合之外，没有任何逻辑关系
集合上的运算主要有：（1）查找某个元素是否存在（2）将集合中的元素排序

1.任何容器都能存储集合
2.常用的表现形式时借鉴于线性表或树。
3.唯一一个仅适合存储和处理集合的数据结构是散列表

集合基本概念

（1）关键字：集合中每个元素都有若干个属性，用它可以标识一个元素。
（2）查找表：由同一类型的元素构成的集合，集合中的元素之间没有任何逻辑关系

一般有三种组织查找表的方法：静态查找表，动态查找表，散列表

（3）静态查找表：查找符合条件的是否在表中，查找某个元素的属性。静态查找表在整个程序的运行期间结构不会变化。

本文主要介绍顺序查找、折半查找和分块查找

（4）动态查找：在查找过程中允许插入查找表中不存在的元素，或者从查找表中删除已存在的某个元素。

本文主要介绍二叉查找树。

（5）平均查找长度：查找过程中对关键码的平均比较次数

静态查找表

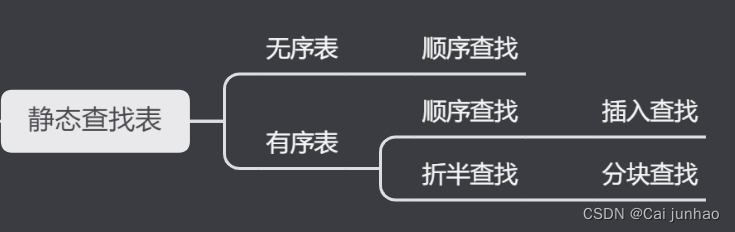
在这里插入图片描述

顺序查找

当查找表中的元素无序时，只能做顺序查找。

顺序表查找

在无序表中set[1…n]中查找关键字为k的元素

算法思想：
将数组set的第一个可用空间置为待查找的关键字k，起到监视哨的作用。查找时，从后向前进行比较，最多比较到下标0位置处，一定会找到一个关键字等于k的元素，这样就省去循环中下标越界的判定。
若查找成功则返回元素的下标，失败则返回0；

template <class RecType>
int seqSearch(vector<RecType> %set, const RecType &k){	//使用STL的vector向量容器
	int i;
	set[0]=k;		//监视哨置为k
	for(i=set.size()-1;k!=set[i];--i);	//从表尾向前查找
	return i;			//成功返回元素的位置，失败返回0
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7

有序表的顺序查找

在有序表set[1…n]中查找关键字为k的元素

假设有序表是按照递增顺序排列的，为减少查找失败时的比较次数，循环条件改为k<set[i],在退出循环后，增加了if语句判断是否找到关键字等于k的元素。

template <class RecType>
int sortedSeqSearch(vector<RecType> &set, const RecType &k){
	int i;
	set[0]=k;
	for(i=set.size()-1;k<set[i];--i);
	if(k==set[i])	return i;
	return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8

顺序查找的缺点时平均查找长度较大，时间复杂度为O(n)
它的优点是算法简单且适合面广，对表的结构无任何要求。

折半查找

又称二分查找

要求查找表有序，级元素按关键字有序，且必须是顺序存储的。

算法思想：
将给定关键字k与有序表的中间位置上的位置进行比较，若相等，则查找成功；否则中间元素将有序表分为两个部分，前一部分的元素均小于中间元素，后一部分均大于中间元素。
在这里插入图片描述

步骤：
（1）置查找范围初值，low=1,high=n
（2）计算中间项，mid=(low+high)/2
（3）将待查找关键字k与中间项的关键字比较：若相等则查找成功，返回中间项的下标mid；若k小于中间项关键字，则low指针不变，high指针更新为mid-1；若k大于中间项关键字，则high指针不变，low指针更新为mid+1
（4）重复步骤二三直到查找成功，返回mid值。若查找失败，返回0.

非递归折半查找

在有序表中set[1…n]中查找关键字为k的元素

template <class RecType>
int binarySearch(const vector<RecType> &set, const RecType &k){
	int low=1, high=set.size()-1,mid;	
	while(low<=high){			//查找范围不为空
		mid=(low+high)/2;		//计算中间位置
		if(k==set[mid])	return min;		//查找成功
		if(k<set[mid])	high=mid-1;		//继续在前半区查找，修改high
		else low = mid+1;				//继续在后半区查找，修改low
	}
	return 0;			//查找失败
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11

递归折半查找

在有序表set[1…n]中查找关键字为k的元素

template <class RecType>
int binarySearch2(const vector<RecType> &set, const RecType &k, int low, int high){
	if(low>high)	return 0;		//递归出口1，查找失败
	int mid=(low+high)/2;		//计算中间位置
	
	if(k==set[mid])	return min;		//递归出口2，查找成功
	else if(k<set[mid])	
		return binarySearch2(set,k,low,mid-1);		//递归在前半区查找
	else return binarySearch2(set,k,mid+1,high);	//递归在后半区查找
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10

折半查找的优点是比较次数少，查找次数快，时间复杂性为O(logn)。缺点是要求待查找表为有序表

分块查找

又称是索引索引顺序查找。是顺序查找方法的改进，其目的是缩小查找范围来改进顺序查找的性能。

把整个有序表分为若干块B1B2…Bn,当i<j时，BI的关键字都小于Bj中元素的关键字，块内的元素可以是有序或无序存储的，但块之间必须是有序的。
分块之后，会建立一个索引表。每个块中在索引表中有一项，称为索引项。
索引项有两个域，用于存放块中元素关键字的最大值和块的第一个元素在索引表中的位置。
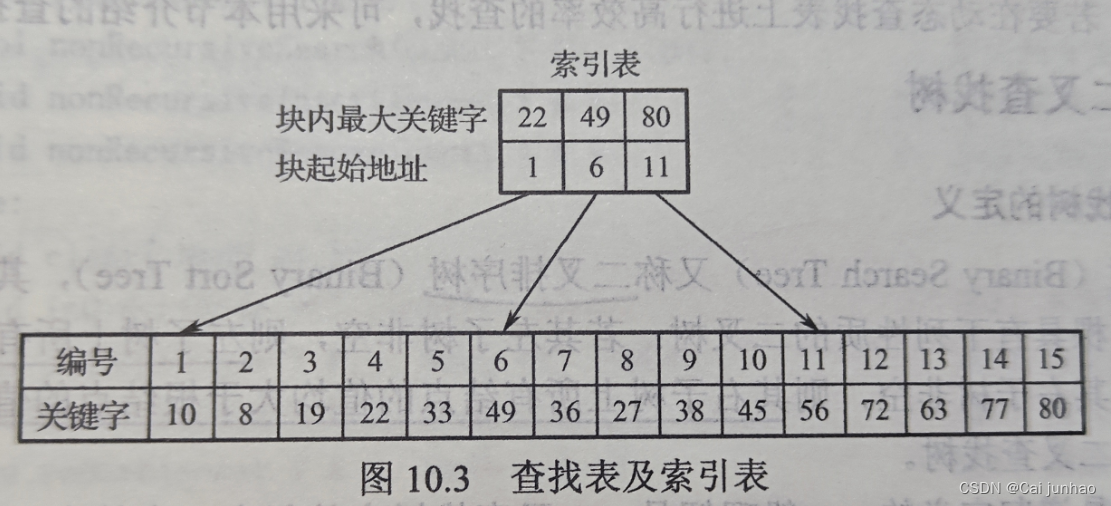
在这里插入图片描述

分块查找的基本过程：
（1）在索引表查找，将待查关键字k与索引表中的关键字进行比较，确定所在的块，可以用顺序查找或折半查找。
（2）然后再块内查找，若块内有序，则折半查找；若无序，则顺序查找。

动态查找表

二叉查找树

又称二叉排序树。

二叉查找树是一颗二叉树，左子树上所有结点的值均小于根结点的值，右子树上所有结点的值均小于根结点的值。

二叉查找树的二叉链表的类型定义：

template <class T>
class BinarySearchTree{
private:
	struct Node{
		T data;		//关键字域
		Node *left, *right;		//左，右孩子指针
		Node(const T & value, Node *lt=NULL, Node *rt=NULL){
			data=value,left=lt,right=rt;	
		}
	};
	Node *root;		//指向根结点的指针

public:
	BinarySearchTree(Node *t=NULL){root=t;}
	~BinarySearchTree(){if(root)	clear(root);	root=NULL;}
	void inOrderTraverse() const;	//中序遍历的公共接口
	bool search(const T & k) const{ return search(k,root); }//递归查找的公有接口
	void insert(const T & k) {insert(k,root);}		//递归插入的公有接口
	void remove(const T & k){remove(k,root);}		//递归删除的公有接口
	bool nonRecursiveSearch(const T &k) const{return nonRecursiveSearch(k, root);}	//非递归查找的公有接口
	void nonRecursiveInsert(const T &k){nonRecursiveInsert(k,root);}		//非递归插入的公有接口
	void nonRecursiveRemove(const T &k){nonRecursiveRemove(k,root);}		//非递归删除的公有接口
	
private:
	void clear(Node *t);
	void inOrder(Node *t) const;				//递归，中序遍历输出有序序列
	bool search(const T & k, Node *t) const;		//递归，查找值为k的结点
	void insert(const T & k,Node * & t);		//递归，插入值为k的结点
	void remove(const T & k,Node * & t);		//递归，删除值为k的结点
	bool nonRecursiveSearch(const T &k,Node *t) const;	//非递归，查找值为k的结点
	void nonRecursiveInsert(const T &k,Node *&t);		//非递归，插入值为k的结点
	void nonRecursiveRemove(const T &k,Node *&t);		//非递归，删除值为k的结点
	void visited(Node *t)const{cout<<t->data<<' ';}		
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34

查找

递归查找

在根指针t所指二叉树中查找关键字等于k的元素，若查找成功，则返回true,否则返回false。

template <class T>
bool BinarySearchTree<T>::search(const T & k, Node *t)const{
	if(t==NULL)	return false;
	else if(k<t->data)	return search(k,t->left);
	else if(k>t->data)	return search(k,t->rigth);
	else return true;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
非递归查找

在根指针t所指二叉树中非递归查找关键字等于k的元素，若查找成功，则返回true,否则返回false

template <class T>
bool BinarySearchTree<T>::nonRecursiveSearch(const T &k,Node *t) const{
	while(t){
		if(k<t->data)	t=t->left;
		else if(k>t->data)	t=t->right;
		else return true;
	}
	return false;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9

二叉树的查找过程，实际上是走了一条从根结点到关键字等于k的元素所在结点的路径，所需要的比较次数为结点所在的层次数。
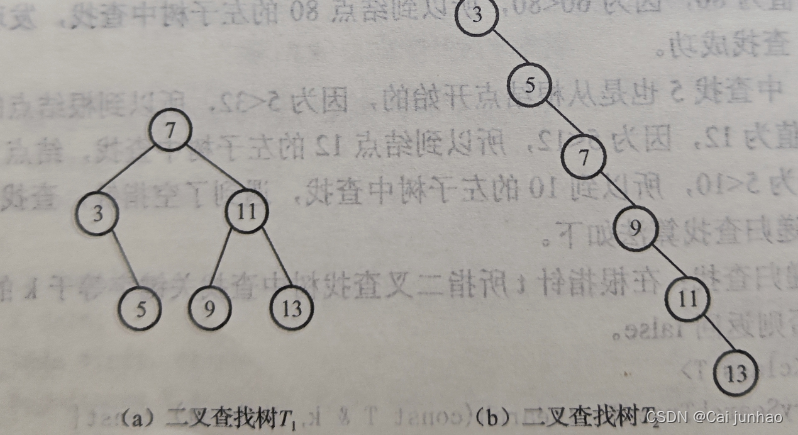
在这里插入图片描述
树T1查找成功的平均查找长度为：ASL=（1x1+2x2+3x3）/6=14/6=2.33
树T2查找成功的平均查找长度为：ASL=（1x1+1x2+1x3+1x4+1x5+1x6）/6=21/6=3.5

采用二叉树查找树进行查找的效率与二叉树的形态有关。平均查找长度正比于logn。

插入

新插入的结点一定是新添加的叶结点。

递归插入

若二叉树中没有关键字k，则插入，否则直接返回。

template <class T>
void BinarySearchTree<T>::insert(const T & k,Node *&t){
	if(t==NULL)	t=new Node(k,NULL,NULL);
	else if(k<t->data)	insert(k,t->left);
	else if(k>t->data)	insert(k,t->rigth);	
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
非递归插入
template <class T>
void BinarySearchTree<T>::nonRecursiveInsert(const T & k, Node *&t){
	Node *p=t;
	Node *f=NULL;		//f为p的双亲
	while(p){			//查找插入位置
		if(p->data==k)	return;	//已有k，无须插入，直接返回
		f=p;			//f保存当前查找的结点
		p=(k<p->data)?p->left:p->right;
	}
	p=new Node(k,NULL,NULL);		//p指向值为k的新结点
	if(t=NULL)	t=p;
	else if(k<f->data)	f->left=p;
	else f->data=p;	
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14

删除

删除一个结点，不能以该结点为根的子树全删除，只能删除该结点，并保证删除后所得的二叉树仍然满足二叉查找树的性质。即，在二叉查找树中删除一个结点相当于删除有序序列中的一个元素。
（1）若删除叶结点，则直接删除，并将其双亲的相应指针域置空。
（2）若删除的结点只有一个孩子，则用此孩子取代被删结点的位置。
（3）若删除的结点左右两颗子树，则选择右子树的最小结点（或左子树的最大结点），将该结点的数据域赋值给要删除结点的数据域，然后删除右子树的最小结点。

递归删除
template <class T>
void BinarySearchTree<T>::remove(const T & k,Node * & t){
	if(t==NULL)	return;		//递归出口1，没找到值为k的结点
	
	if(k<t->data)	remove(k,t->left);	//继续在左子树中查找k
	else if(k>t->data)	remove(k,t->right);		//继续在右子树中查找k
	else if(t->left!=NULL&&t->right->NULL){		//递归出口2，值为k的结点有左右孩子
		Node *temp=t->left;
		while(temp->right!=NULL)
			temp=temp->right;		//temp为左子树最右结点（左子树最大值）
		t->data=temp->data;			//用temp替换t
		remove(t->data,t->left);	//继续在左子树中删除temp
	}
	else{				//递归出口3，只有一个孩子或没有孩子
		Node *temp=t;
		t=(t->left!=NULL)?t->left:t->right;
		delete temp;
	}
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
非递归删除算法

若二叉树中有关键字为k的结点，则删除它，否则直接退出。

template <class T>
void BinarySearchTree<T>::noRecursiveRemove(const T & k,Node * & t){
	Node* p=t,*f=NULL,*q=NULL,*tmp=NULL;	//f指向被删除结点的双亲
	while(p){
		if(p->data==k)	break;		//找到关键字为k的结点
		f=p;
		p=(k<p->data)?p->left:p->right;
	}
	if(!p)	return;
	if(p->left!=NULL&&p->right!=NULL){	//关键字为k的结点有左、右两个孩子
		f=p;			//f是其双亲
		tmp=p->right;		//tmp成为新的被删结点
		while(tmp->left!=NULL){		//查找右子树最小值（最左结点）
			f=tmp;
			tmp=tmp->left;
		}
		p->data=tmp->data;		//右子树最小结点tmp替换p
		p=tmp;			//tmp成为新的被删结点，p指向tmp
	}
	if(!(p->left!=NULL&&p->right!=NULL)){		//p只有一个孩子或p是叶结点
		q=(p->left!=NULL)?p->left:p->right;
		if(q==t)	t=q;
		else if(f->left==p)	f->left=q;
		else f->right=q;
		}
		delete q;
}	

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27

二叉查找树中的插入和删除运算是基于查找运算的。当二叉查找树的形态和折半查找的判定相同，此时平均查找长度和logn成正比，各算法的最好时间复杂度为O(logn)
最坏情况是，当构造二叉查找树的关键字序列有序时，将构成单支二叉树，此时平均查找长度和顺序查找相同，为(n+1)/2，各算法的最坏时间复杂度为O(n)。

散列表

概念

负载因子a：表空间大小n/表结点数n

a越小，冲突的可能性越小

冲突：某散列表函数对于不相等的关键码计算了相同的散列地址。

不产生冲突的散列表极少

同义词：发生冲突的两个关键码

构造的方法

平方取中法

关键字求平方后，按散列表的表长，取中间的若干位作为散列地址。这是因为关键字求平方后的中间几位数和关键字的每一位都有关。

例如，关键字key=2346，散列地址为3位数，2346x2346=5503716，取中间的037作为散列地址。

除留余数法

把关键字除以某个不大于散列表长度的整数得到的余数作为散列地址。
散列函数形式为：H(key)=key mod p (p<=m)

p若选取不好，容易产生同义词，通常是设为一个小于散列表长度m的最大质数。

解决冲突的方法

闭散列法

又称为开放地址法。一是数组空间是封闭的，发生冲突时不再使用额外的存储单元，即长度是确定的，定义后不能增加；二是每个地址对所有元素都是开放的

基本思想：对于一个待插入散列表的元素，若按给定的散列函数求得基地址H（key）被占用，则按照某种策略寻找另一个散列地址。

当发生冲突时，寻找下一个可用散列地址得过程称为探测。
探测得计算公式：H=(H(key)+di) mod m , i=1,2...k(k<=m-1)
(1)线性探测法
递增序列di=i,即di为1，2，3…,m-1的线性序列

当发生冲突时，依次探测地址为(H(key)+1) mod m，(H(key)+2) mod m，(H(key)+3) mod m…，直到找到 一个空单元，把数据放入该空单元中。顺序查找时，把散列表看成一个循环表，如果探测到了表尾都没有找到空单元，则回到表头继续探测。若探测了所有单元仍未找到空单元，则说明散列表已满，需要进行“溢出”处理。

（2）二次探测法

线性探测法很容易出现堆积，有一长串的连续被占单元，降低了效率。要使得发生冲突的元素的位置较分散，可以加大探测序列的步长。

二次探测法的递增序列di=i2,即di为12，-12,22，-22…k2的线性序列.
当发生冲突时，依次探测地址为(H(key)+1) mod m，(H(key)-1) mod m，(H(key)+2) mod m，(H(key)-2) mod m…,直到找到空单元。

开散列法

将所有关键字为同义词的元素存储在同一单链表中，单链表包含两个域：数据域存储集合中的元素，指针域指向下一个同义词。

散列表的实现

闭散列表的类型定义和运算实现

在闭散列表定义了结点类型Node，每个结点除存储关键字key外，还存储了结点的状态state。

template <class KeyType>
class closeHashTable:public hashTable<KeyType>
private:
	enum NodeState{EMPTY, ACTION, DELETED};	//状态：空、使用中、已删除
	struct Node{			//散列表中的结点类型
		KeyType key;		//关键字
		NodeState state;		//该位置的使用状态
		Node() {state=EMPTY;}
	};
	Node *data;		//散列表
	int maxSize;	//散列表容量
	int curLength;		//当前存放的元素个数
	void resize();		//扩大散列表长度
	
public:         
	closeHashTable(int len=11,int (*h)(const KeyType &k, int maxSize)=defaultHash);
	~closeHashTable(){delete [] data;}
	int size() {return curLength;}		//返回当前元素个数
	int capacity()	{return maxSize;}		//返回表的容量
	bool search(const KeyType &k)	const;		//查找关键字为k的元素是否存在
	int getPos(const KeyType &k) const;			//查找关键字为k的元素的位置
	bool insert(const KeyType &k);			//插入关键字为k的元素
	bool remove(const KeyType &k);		//删除关键字为k的元素
	void print();     		//输出散列表
}                                                  

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
构造函数

行参len为用户指定的数值，利用nextPrime(len)函数求出大于该数值的第一个质数作为散列表的长度；形参h是函数指针，可以通过实参来指定自己的散列函数。

template <class Type>
closeHashTable<KeyTable>::closeHashTable(int len, int (*h)(const KeyType &k, int maxSiz)){
	maxSize=nextPrime(len);
	data=new Node[maxSize];
	hash=h;
	curLength=0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
查找1

查找关键字为k的元素是否在散列表中，查找成功返回true，查找失败返回false.

template <class KeyType>
cool closeHashTable<KeyType>::search(const KeyType &k) const{
	int offset=1;
	int pos=hash(k,maxSize);		//关键字为k的元素的基地址
	while(data[pos].state==ACTIVE){	//该地址处于使用中状态
		if(data[pos].key!=k)			//pos位置的关键字不等于k
			pos=(pos+offset)%maxSize;	//计算下一刻散列地址
		else 
			return true;			
	}
	return fasle;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
查找2

查找散列表中关键字为k的元素的散列地址，如果找到了该元素，则返回它的散列地址，否则返回-1

template <class KeyType>
int closeHashType<KeyType>::getPos(const KeyType & k)const{
	int offset=1;
	int pos=hash(k,maxSize);
	while(data[pos].state==ACTIVE){
		if(data[pos].key!=k)
			pos=(pos+offset)%maxSize;
		else 
			return pos;
	}
	return -1;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
插入

插入关键字为k的元素到散列表中，若已存在则退出程序并返回false，否则插入元素并返回ture

template <class KeyType>
bool closeHashTable<KeyType>::insert(const KeyType &k){
	int offset=1;
	int pos;

	if(curLength>maxSize/2)	reisze();	//装填因子大于0.5时扩充表空间
	pos=hash(k, maxSize);
	while(data[pos].state==ACTIVE){		///查找可用空间
		if(data[pos].key!=k)			//被其他元素占用，发生冲突
			pos=(pos+offset)%maxSize;		//求下一个散列地址
		else 
			return false;			//该元素已经存在
	}							//退出循环时data[pos].state!=ACTIVATE
	data[pos].key=k;			//保存关键字k
	data[pos].state=ACTIVE;		//状态改为ACTIVATE
	curLength++;			//元素个数增加
	return true;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
删除

删除散列表中关键字为k的元素，若删除失败则返回false，否则返回ture

template <class KeyType>
bool closeHashTable<KeyType>::remove(const KeyType &k){
	int pos=getPos(k);		//调用getPos求散列地址
	if(pos!=-1){
		data[pos].state=DELETED;		//懒惰删除，仅将状态改为DELETE
		curLength--;
		return true;
	}
	else
		return false;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
扩大表空间
template <class KeyType>
void closeHashTable<KeyType>::resize(){
	Node *tmp=data;
	int oldSize=maxSize;
	maxSize=nextPrime(2*oldSize);
	data=new Node[maxSize];
	
	for(int i=0;i<oldSize;++i){
		if(tmp[i].state==ACTIVETE){
			insert(tmp[i].key);		//执行insert会使curLength++
			curLength--;		//重新将元素插入进去，不能改变当前长度
		}
	}
	delete [] tmp;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
输出散列表

遍历散列表，输出标记为ACTIVETE的元素。

template <class KeyType>
void closeHashTable<KeyType>::print(){
	int pos;
	cout<<"输出闭散列表中的内容："<<endl;
	for(pos=0;pos<maxSize;++pos){
		if(data[pos].state==ACTIVE)
			cout<<pos<<": "<<data[pos].key<<"\t\t";
	}
	cout<<endl;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10

开散列表的类型定义和运算实现

template <class Type>
class openHashTable:public hashTable<Type>{
private:
	struct Node{
		Type key;		//关键字域
		Node *next;		//指针域
		Node () {next=NULL;}
		Node (const Type &d){key=d; next=NULL;}
	};
	Node** data;		//散列表数组，数组元素为Node型的指针
	int maxSize;		//容量
	int curLength;		//当前存储的元素个数
	void resize();		//扩大表空间

public:
	openHashTable(int len=11, int (*h)(const Type & k, int maxSize)=defaultHash);
	~openHashTable();
	int size() {return curLength;}		//返回当前元素个数
	int capacity() {return maxSize;}	//返回表容量
	bool search(const Type &k)const;	
	bool insert(const Type &k);
	bool remove(const Type &k);
	void print();
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
构造函数
template <class Type>
openHashTable<Type>::openHashTable(int len=11, int (*h)(const Type & k, int maxSize)){
	hash=h;
	curLength=0;
	maxSize=nextPrime(len);
	data=new Node*[maxSize];		//用于存放头执政的散列表数组
	
	for(int i=0;i<maxSize;++i)
		data[i]=new Node;	//为每个单链表申请头结点
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
析构函数

释放每个单链表及散列表数组

template <class Type>
openHashTable<Type>::~openHashTable(){
	for(int i=0;i<maxSize;++i){
		Node *p=data[i];
		while(p){
			Node *tmp=p->next;
			delete p;
			p=tmp;
		}
	}
	delete [] data;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
查找

查找关键字为k的元素是否在散列表中，查找成功返回true，查找失败返回false.

template <class Type>
bool openHashTable<Type>::search(const Type &k)const{
	int pos=hash(k, maxSize);
	Node *p=data[pos]->next;
	while(p!=NULL&&p->next!=k)	
		p=p->next;
	if(p!=NULL)	return true;
	else return false;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
插入

插入关键字为k的元素到散列表中，若已存在则退出程序并返回false，否则插入元素并返回ture

template <class Type>
bool openHashTable<Type>::insert(const Type &k){
	if(curLength+1>maxSize)	resize();
	int pos=hash(k,maxSize);
	Node *p=data[pos]->next;	
	while(p!=NULL&&p->key!=k)		//查找关键字为k的元素
		p=p->next;

	if(p==NULL){
		p=new Node(k);
		p->next=data[pos]->next;		//在表头插入该元素
		data[pos]->next=p;
		curLength++;
		return true;
	}
	return false;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
删除

删除散列表中关键字为k的元素，若删除失败则返回false，否则返回ture

template <class Type>
bool openHashTable<Type>::remove(const Type &k){
	int pos=hash(k,maxSize);
	Node *pre=data[pos],*p;
	while(pre->next!=NULL&&pre->key!=k)
		pre=pre->next;
	if(pre->next==NULL)	return false;
	else{
		p->pre->next;
		pre->next=p->next;
		delete p;
		curLength--;
		return true;
	}
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
扩大散列表空间
template <class Type>
void openHashTable<Type>::resize(){
	Node **tmp=data,*p,*q;
	int i,pos,oldSize=maxSize;
	maxSize=nextPrime(2*oldSize);	//找到下一个质数
	data=new Node*[maxSize];
	
	for(i=0;i<maxSize;++i)	//设立新的散列表数组
		data[i]=new Node;		
	for(i=0;i<oldSize;++i){		//处理原散列表
		p=tmp[i]->next;		//p指向一个单链表的首元结点
		while(p){		//吹里该单链表中的每个结点
			pos=hash(p=>key,maxSize);		//计算p所值向结点的新hash地址
			q=p->next;		//q保存p的后继
			p->next=data[pos]->next;	//在新hash地址的表头插入p结点
			data[pos]->next=p;
			p=q;		//准备处理下一个结点
		}
	}
	for(i=0;i<oldSize;++i)
		delete tmp[i];
	
	delete []tmp;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
输出散列表
template <class Type>
void openHashTable<Type>::print(){
	int i;
	Node *p;
	cout<<"输出开散列表中的内容: "<<endl;
	for(i=0;i<maxSize;++i){
		p=data[i]->next;		//p指向一个单链表的首元结点
		cout<<i<<":";
		while(p){
			cout<<"->"<<p->key;
			p=p->next;
		}
		cout<<endl;
	}
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15

习题

1.在有序表A[1…20]中，按折半查找方法进行查找，查找长度为4的元素的下标从小到大依次是( )

二叉查找树如下:
1 a10
2 a5 a15
3 a2 a7 a12 a18
4 a1 a3 a6 a8 a11 a13 a16 a19
5 a4 a9 a14 a17 a20

答案：1，3，6，8，11，13，16，19

2.下列正确的是()
A.在二叉树中插入一个新结点，总是插入叶结点下面。
B.Hash表的平均查找长度与处理冲突的方法无关
C.采用线性探测法处理散列是的冲突，当从哈希表中删除一个记录时，不应将这个记录的所在位置置空，因为这会影响以后的查找
D.随着装填因子a的增大,用闭散列表解决冲突,其平均搜索长度比用开散列表法解决冲突时的平均搜索偿付增长得慢

选C

3.哈希表长为14,哈希函数H(key)=key % 11.表中已有 4个结点,a(15)=4,a(38)=5,a(61)=6,a(84)=7,其余地址为空,若用二次探测再散列得方法处理冲突,求关键字为49的结点地址()

H1=19%11=5
H2=(5+12)%11=6
H2=(5+22)%11=9

答案是9

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/小丑西瓜9/article/detail/561233
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号