OFDM通信链路matlab仿真_ofdm调制 matlab

UP目录

一、理论基础

二、核心程序

三、测试结果

---

一、理论基础

        OFDM(Orthogonal Frequency Division Multiplexing)即正交频分复用技术，实际上OFDM是MCM(Multi Carrier Modulation)，多载波调制的一种。通过频分复用实现高速串行数据的并行传输, 它具有较好的抗多径衰落的能力，能够支持多用户接入。OFDM技术由MCM（Multi-Carrier Modulation，多载波调制）发展而来。OFDM技术是多载波传输方案的实现方式之一，它的调制和解调是分别基于IFFT和FFT来实现的，是实现复杂度最低、应用最广的一种多载波传输方案。

      OFDM主要思想是：将信道分成若干正交子信道，将高速数据信号转换成并行的低速子数据流，调制到在每个子信道上进行传输。正交信号可以通过在接收端采用相关技术来分开，这样可以减少子信道之间的相互干扰(ISI) 。每个子信道上的信号带宽小于信道的相关带宽，因此每个子信道上可以看成平坦性衰落，从而可以消除码间串扰，而且由于每个子信道的带宽仅仅是原信道带宽的一小部分，信道均衡变得相对容易。

       OFDM是一种特殊的多载波传输方案。OFDM应用DFT和其逆变换IDFT方法解决了产生多个互相正交的子载波和从子载波中恢复原信号的问题。这就解决了多载波传输系统发送和传送的难题。应用快速傅里叶变换更使多载波传输系统的复杂度大大降低。从此OFDM技术开始走向实用。但是应用OFDM系统仍然需要大量繁杂的数字信号处理过程，而当时还缺乏数字处理功能强大的元器件，因此OFDM技术迟迟没有得到迅速发展。

基于IFFT/FFT 实现的OFDM 系统:

       OFDM采用BPSK、QPSK、16QAM、64QAM4种调制方式。按照星座图，将每个子信道上的数据，映射到星座图点的复数表示，转换为同相Ich和正交分量Qch。

       其实这是一种查表的方法，以16QAM星座为例，bits_per_symbol=4，则每个OFDM符号的每个子信道上有4个二进制数{d1,d2,d3,d4},共有16种取值，对应星座图上16个点，每个点的实部记为Qch。为了所有的映射点有相同高的平均功率，输出要进行归一化，所以对应BPSK,PQSK,16QAM,64QAM，分别乘以归一化系数系数1，, , .输出的复数序列即为映射后的调制结果。

        对上一步得到的相同分量和正交分量按照（Ich+Qch*i）进行IFFT运算。并将得到的复数的实部作为新的Ich，虚部作为新的Qch。

         在实际运用中， 信号的产生和解调都是采用数字信号处理的方法来实现的， 此时要对信号进行抽样， 形成离散时间信号。 由于OFDM信号的带宽为B=N·Δf， 信号必须以Δt=1/B=1/(N·Δf)的时间间隔进行采样。 采样后的信号用sn,i

      t=1/B=1/(N·Δf)的时间间隔进行采样。 采样后的信号用sn,i表示， i = 0, 1, …, N-1，则有

        从该式可以看出，它是一个严格的离散反傅立叶变换（IDFT）的表达式。IDFT可以采用快速反傅立叶变换(IFFT)来实现 

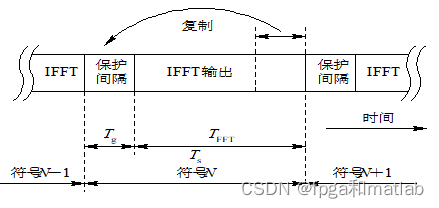
         由IFFT运算后的每个符号的同相分量和正交分量分别转换为串行数据，并将符号尾部G长度的数据加到头部，构成循环前缀。如果加入空的间隔，在多径传播的影响下，会造成载波间干扰ICI。保护见个的长度G应该大于多径时的扩张的最大值。

二、核心程序

.........................................................................
baseband_out_length = carrier_count * symbols_per_carrier * bits_per_symbol;%所输入的比特数目
 
carriers = (1:carrier_count) + (floor(IFFT_bin_length/4) - floor(carrier_count/2));% 共轭对称子载波映射  复数数据对应的IFFT点坐标
 
conjugate_carriers = IFFT_bin_length - carriers + 2;%共轭对称子载波映射  共轭复数对应的IFFT点坐标
...................................................................................
 
XX=zeros(symbols_per_carrier,IFFT_bin_length+GI+GIP);
 
for k=1:symbols_per_carrier;
 
    for i=1:IFFT_bin_length;
 
        XX(k,i+GI)=signal_after_IFFT(k,i);
 
    end
 
    for i=1:GI;
 
        XX(k,i)=signal_after_IFFT(k,i+IFFT_bin_length-GI);%添加循环前缀
 
    end
 
    for j=1:GIP;
 
        XX(k,IFFT_bin_length+GI+j)=signal_after_IFFT(k,j);%添加循环后缀
 
    end
 
end
 
time_wave_matrix_cp=XX;%添加了循环前缀与后缀的时域信号矩阵,此时一个OFDM符号长度为IFFT_bin_length+GI+GIP=660
 
%==============OFDM符号加窗==========================================
 
windowed_time_wave_matrix_cp=zeros(1,IFFT_bin_length+GI+GIP);
 
for i = 1:symbols_per_carrier
 
windowed_time_wave_matrix_cp(i,:) = real(time_wave_matrix_cp(i,:)).*rcoswindow(beta,IFFT_bin_length+GI)';%加窗  升余弦窗
end 
%========================生成发送信号，并串变换==================================================
windowed_Tx_data=zeros(1,symbols_per_carrier*(IFFT_bin_length+GI)+GIP);
windowed_Tx_data(1:IFFT_bin_length+GI+GIP)=windowed_time_wave_matrix_cp(1,:);
for i = 1:symbols_per_carrier-1 ;
    windowed_Tx_data((IFFT_bin_length+GI)*i+1:(IFFT_bin_length+GI)*(i+1)+GIP)=windowed_time_wave_matrix_cp(i+1,:);%并串转换，循环后缀与循环前缀相叠加
end
.................................................................................
Rx_data_matrix=zeros(symbols_per_carrier,IFFT_bin_length+GI+GIP);
for i=1:symbols_per_carrier;
    Rx_data_matrix(i,:)=Rx_data(1,(i-1)*(IFFT_bin_length+GI)+1:i*(IFFT_bin_length+GI)+GIP);%串并变换
end
Rx_data_complex_matrix=Rx_data_matrix(:,GI+1:IFFT_bin_length+GI);%去除循环前缀与循环后缀，得到有用信号矩阵
%==============================================================
%                      OFDM解码   16QAM解码
%=================FFT变换=================================
Y1=fft(Rx_data_complex_matrix,IFFT_bin_length,2);%OFDM解码 即FFT变换
Rx_carriers=Y1(:,carriers);%除去IFFT/FFT变换添加的0，选出映射的子载波
Rx_phase =angle(Rx_carriers);%接收信号的相位
Rx_mag = abs(Rx_carriers);%接收信号的幅度
figure(4);
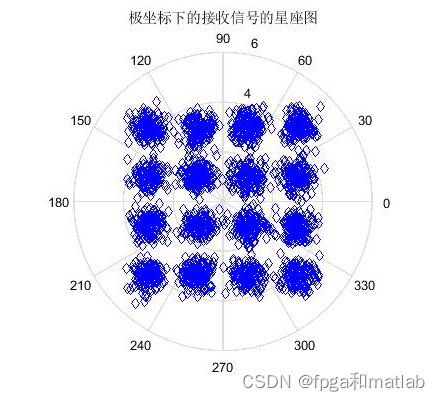
polar(Rx_phase, Rx_mag,'bd');%极坐标坐标下画出接收信号的星座图
title('极坐标下的接收信号的星座图')
%======================================================================
[M, N]=pol2cart(Rx_phase, Rx_mag);
Rx_complex_carrier_matrix = complex(M, N);
figure(5);
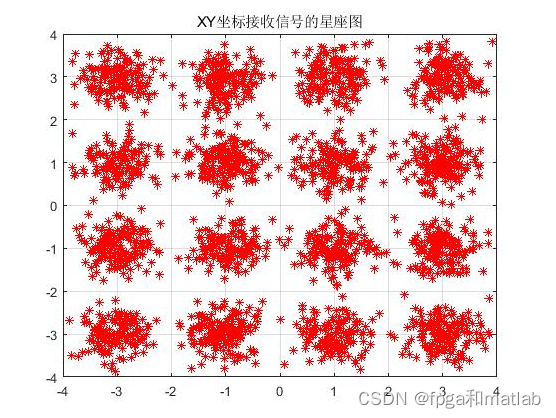
plot(Rx_complex_carrier_matrix,'*r');%XY坐标接收信号的星座图
title('XY坐标接收信号的星座图')
axis([-4, 4, -4, 4]);
grid on
%====================16qam解调=======================================
............................................................................
up107

三、测试结果