小丑西瓜9

这个屌丝很懒，什么也没留下！

热门标签

（代码中使用拆分的方式实现多头注意力）详解Transformer中Self-Attention以及Multi-Head Attention_多头注意力是怎么切分的

作者：小丑西瓜9 | 2024-02-16 11:54:56

踩

多头注意力是怎么切分的

原文链接：https://blog.csdn.net/qq_37541097/article/details/117691873

原文名称：Attention Is All You Need
原文链接：https://arxiv.org/abs/1706.03762

如果不想看文章的可以看下我在b站上录的视频：https://b23.tv/gucpvt

最近Transformer在CV领域很火，Transformer是2017年Google在Computation and Language上发表的，当时主要是针对自然语言处理领域提出的（之前的RNN模型记忆长度有限且无法并行化，只有计算完

     t
    
    
     i
    
   
  
  
   t_i
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.76508em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathdefault">t</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>时刻后的数据才能计算<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     t
    
    
     
      i
     
     
      +
     
     
      1
     
    
   
  
  
   t_{i+1}
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.823411em; vertical-align: -0.208331em;"></span><span class="mord"><span class="mord mathdefault">t</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span class="mbin mtight">+</span><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.208331em;"><span class=""></span></span></span></span></span></span></span></span></span></span>时刻的数据，但Transformer都可以做到）。在这篇文章中作者提出了<code onclick="mdcp.copyCode(event)" style="user-select: auto;">Self-Attention</code>的概念，然后在此基础上提出<code onclick="mdcp.copyCode(event)" style="user-select: auto;">Multi-Head Attention</code>，所以本文对<code onclick="mdcp.copyCode(event)" style="user-select: auto;">Self-Attention</code>以及<code onclick="mdcp.copyCode(event)" style="user-select: auto;">Multi-Head Attention</code>的理论进行详细的讲解。在阅读本文之前，建议大家先去看下李弘毅老师讲的Transformer的内容。本文的内容是基于李弘毅老师讲的内容加上自己阅读一些源码进行的总结。</p> 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

前言

如果之前你有在网上找过self-attention或者transformer的相关资料，基本上都是贴的原论文中的几张图以及公式，如下图，讲的都挺抽象的，反正就是看不懂（可能我太菜的原因）。就像李弘毅老师课程里讲到的"不懂的人再怎么看也不会懂的"。那接下来本文就结合李弘毅老师课上的内容加上原论文的公式来一个个进行详解。

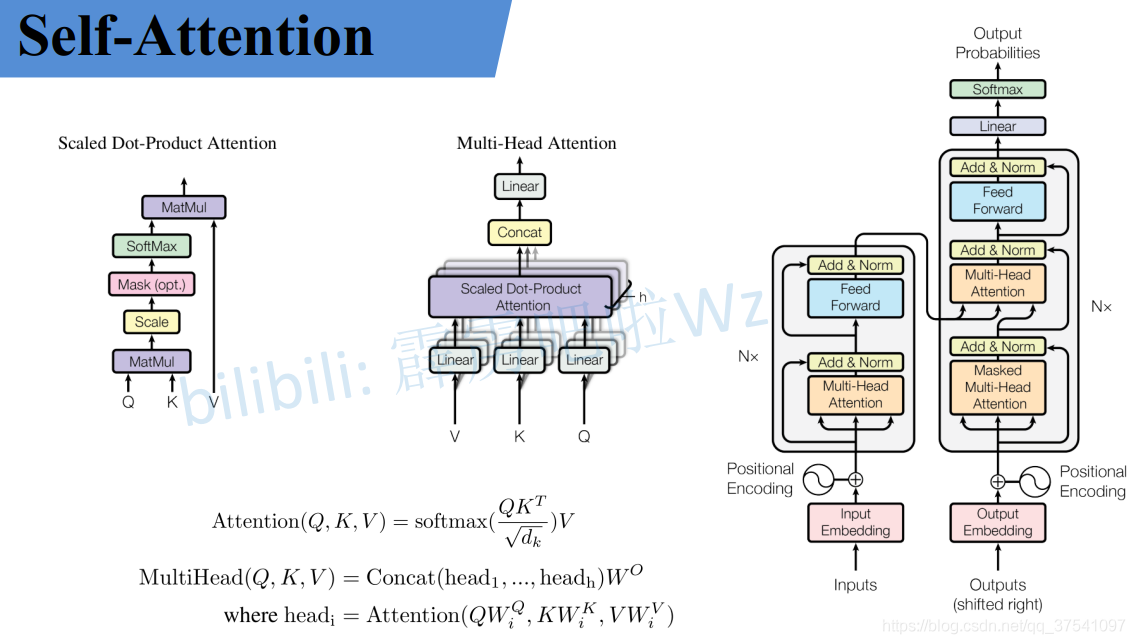
attention is all you need

Self-Attention

下面这个图是我自己画的，为了方便大家理解，假设输入的序列长度为2，输入就两个节点

     x
    
    
     1
    
   
   
    ,
   
   
    
     x
    
    
     2
    
   
  
  
   x_1, x_2
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.625em; vertical-align: -0.19444em;"></span><span class="mord"><span class="mord mathdefault">x</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span class="mord mathdefault">x</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>，然后通过Input Embedding也就是图中的<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    f
   
   
    (
   
   
    x
   
   
    )
   
  
  
   f(x)
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span style="margin-right: 0.10764em;" class="mord mathdefault">f</span><span class="mopen">(</span><span class="mord mathdefault">x</span><span class="mclose">)</span></span></span></span></span>将输入映射到<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     a
    
    
     1
    
   
   
    ,
   
   
    
     a
    
    
     2
    
   
  
  
   a_1, a_2
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.625em; vertical-align: -0.19444em;"></span><span class="mord"><span class="mord mathdefault">a</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span class="mord mathdefault">a</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>。紧接着分别将<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     a
    
    
     1
    
   
   
    ,
   
   
    
     a
    
    
     2
    
   
  
  
   a_1, a_2
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.625em; vertical-align: -0.19444em;"></span><span class="mord"><span class="mord mathdefault">a</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span class="mord mathdefault">a</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>分别通过三个变换矩阵<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     W
    
    
     q
    
   
   
    ,
   
   
    
     W
    
    
     k
    
   
   
    ,
   
   
    
     W
    
    
     v
    
   
  
  
   W_q, W_k, W_v
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.969438em; vertical-align: -0.286108em;"></span><span class="mord"><span style="margin-right: 0.13889em;" class="mord mathdefault">W</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.151392em;"><span class="" style="top: -2.55em; margin-left: -0.13889em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span style="margin-right: 0.03588em;" class="mord mathdefault mtight">q</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span style="margin-right: 0.13889em;" class="mord mathdefault">W</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.336108em;"><span class="" style="top: -2.55em; margin-left: -0.13889em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span style="margin-right: 0.13889em;" class="mord mathdefault">W</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.151392em;"><span class="" style="top: -2.55em; margin-left: -0.13889em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span style="margin-right: 0.03588em;" class="mord mathdefault mtight">v</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>（这三个参数是可训练的，是共享的）得到对应的<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     q
    
    
     i
    
   
   
    ,
   
   
    
     k
    
    
     i
    
   
   
    ,
   
   
    
     v
    
    
     i
    
   
  
  
   q^i, k^i, v^i
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.0191em; vertical-align: -0.19444em;"></span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">q</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.824664em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span style="margin-right: 0.03148em;" class="mord mathdefault">k</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.824664em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">v</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.824664em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span></span></span></span></span></span></span></span></span></span>（这里在源码中是直接使用全连接层实现的，这里为了方便理解，忽略偏执）。</p> 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178

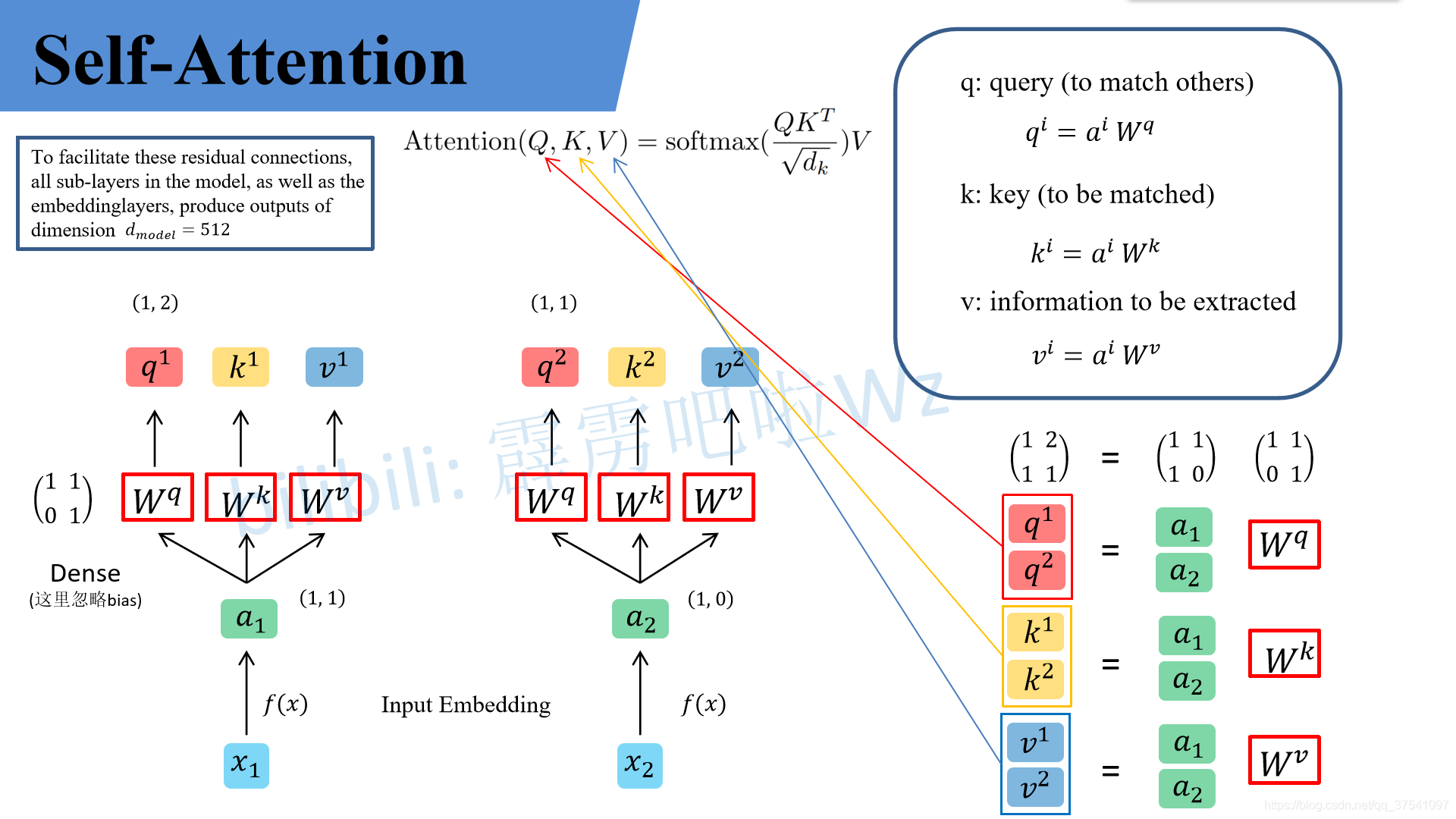
self-attention

其中

     q
    
   
   
    q
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.625em; vertical-align: -0.19444em;"></span><span style="margin-right: 0.03588em;" class="mord mathdefault">q</span></span></span></span></span>代表query，后续会去和每一个<span class="katex--inline"><span class="katex"><span class="katex-mathml">
 
  
   
    
     k
    
   
   
    k
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.69444em; vertical-align: 0em;"></span><span style="margin-right: 0.03148em;" class="mord mathdefault">k</span></span></span></span></span>进行匹配</li><li><span class="katex--inline"><span class="katex"><span class="katex-mathml">
 
  
   
    
     k
    
   
   
    k
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.69444em; vertical-align: 0em;"></span><span style="margin-right: 0.03148em;" class="mord mathdefault">k</span></span></span></span></span>代表key，后续会被每个<span class="katex--inline"><span class="katex"><span class="katex-mathml">
 
  
   
    
     q
    
   
   
    q
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.625em; vertical-align: -0.19444em;"></span><span style="margin-right: 0.03588em;" class="mord mathdefault">q</span></span></span></span></span>匹配</li><li><span class="katex--inline"><span class="katex"><span class="katex-mathml">
 
  
   
    
     v
    
   
   
    v
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.43056em; vertical-align: 0em;"></span><span style="margin-right: 0.03588em;" class="mord mathdefault">v</span></span></span></span></span>代表从<span class="katex--inline"><span class="katex"><span class="katex-mathml">
 
  
   
    
     a
    
   
   
    a
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.43056em; vertical-align: 0em;"></span><span class="mord mathdefault">a</span></span></span></span></span>中提取得到的信息</li></ul> 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68

假设

     a
    
    
     1
    
   
   
    =
   
   
    (
   
   
    1
   
   
    ,
   
   
    1
   
   
    )
   
   
    ,
   
   
    
     a
    
    
     2
    
   
   
    =
   
   
    (
   
   
    1
   
   
    ,
   
   
    0
   
   
    )
   
   
    ,
   
   
    
     W
    
    
     q
    
   
   
    =
   
   
    
     (
    
    
     
      
       1
      
      
       ,
      
      
       1
      
     
     
      
       0
      
      
       ,
      
      
       1
      
     
    
    
     )
    
   
  
  
   a_1=(1, 1), a_2=(1,0), W^q= \binom{1, 1}{0, 1}
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.58056em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathdefault">a</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord">1</span><span class="mclose">)</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span class="mord mathdefault">a</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord">0</span><span class="mclose">)</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span style="margin-right: 0.13889em;" class="mord mathdefault">W</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.664392em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span style="margin-right: 0.03588em;" class="mord mathdefault mtight">q</span></span></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 1.37622em; vertical-align: -0.481108em;"></span><span class="mord"><span class="mopen delimcenter" style="top: 0em;"><span class="delimsizing size1">(</span></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.895108em;"><span class="" style="top: -2.355em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">0</span><span class="mpunct mtight">,</span><span class="mord mtight">1</span></span></span></span><span class="" style="top: -3.144em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span><span class="mpunct mtight">,</span><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.481108em;"><span class=""></span></span></span></span></span><span class="mclose delimcenter" style="top: 0em;"><span class="delimsizing size1">)</span></span></span></span></span></span></span>那么：<br> <span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
 
  
   
    
     
      q
     
     
      1
     
    
    
     =
    
    
     (
    
    
     1
    
    
     ,
    
    
     1
    
    
     )
    
    
     
      (
     
     
      
       
        1
       
       
        ,
       
       
        1
       
      
      
       
        0
       
       
        ,
       
       
        1
       
      
     
     
      )
     
    
    
     =
    
    
     (
    
    
     1
    
    
     ,
    
    
     2
    
    
     )
    
    
     ,
    
    
     &nbsp;&nbsp;&nbsp;
    
    
     
      q
     
     
      2
     
    
    
     =
    
    
     (
    
    
     1
    
    
     ,
    
    
     0
    
    
     )
    
    
     
      (
     
     
      
       
        1
       
       
        ,
       
       
        1
       
      
      
       
        0
       
       
        ,
       
       
        1
       
      
     
     
      )
     
    
    
     =
    
    
     (
    
    
     1
    
    
     ,
    
    
     1
    
    
     )
    
   
   
     q^1 = (1, 1) \binom{1, 1}{0, 1} =(1, 2) , \ \ \ q^2 = (1, 0) \binom{1, 1}{0, 1} =(1, 1) 
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.05855em; vertical-align: -0.19444em;"></span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">q</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.864108em;"><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 2.40003em; vertical-align: -0.95003em;"></span><span class="mopen">(</span><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord">1</span><span class="mclose">)</span><span class="mord"><span class="mopen delimcenter" style="top: 0em;"><span class="delimsizing size3">(</span></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.32144em;"><span class="" style="top: -2.314em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord">0</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord">1</span></span></span><span class="" style="top: -3.677em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.88044em;"><span class=""></span></span></span></span></span><span class="mclose delimcenter" style="top: 0em;"><span class="delimsizing size3">)</span></span></span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 1.11411em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord">2</span><span class="mclose">)</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mspace">&nbsp;</span><span class="mspace">&nbsp;</span><span class="mspace">&nbsp;</span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">q</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.864108em;"><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 2.40003em; vertical-align: -0.95003em;"></span><span class="mopen">(</span><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord">0</span><span class="mclose">)</span><span class="mord"><span class="mopen delimcenter" style="top: 0em;"><span class="delimsizing size3">(</span></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.32144em;"><span class="" style="top: -2.314em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord">0</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord">1</span></span></span><span class="" style="top: -3.677em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.88044em;"><span class=""></span></span></span></span></span><span class="mclose delimcenter" style="top: 0em;"><span class="delimsizing size3">)</span></span></span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord">1</span><span class="mclose">)</span></span></span></span></span></span><br> 前面有说Transformer是可以并行化的，所以可以直接写成：<br> <span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
 
  
   
    
     
      (
     
     
      
       
        q
       
       
        1
       
      
      
       
        q
       
       
        2
       
      
     
     
      )
     
    
    
     =
    
    
     
      (
     
     
      
       
        1
       
       
        ,
       
       
        1
       
      
      
       
        1
       
       
        ,
       
       
        0
       
      
     
     
      )
     
    
    
     
      (
     
     
      
       
        1
       
       
        ,
       
       
        1
       
      
      
       
        0
       
       
        ,
       
       
        1
       
      
     
     
      )
     
    
    
     =
    
    
     
      (
     
     
      
       
        1
       
       
        ,
       
       
        2
       
      
      
       
        1
       
       
        ,
       
       
        1
       
      
     
     
      )
     
    
   
   
     \binom{q^1}{q^2} = \binom{1, 1}{1, 0} \binom{1, 1}{0, 1} = \binom{1, 2}{1, 1} 
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 2.44114em; vertical-align: -0.95003em;"></span><span class="mord"><span class="mopen delimcenter" style="top: 0em;"><span class="delimsizing size3">(</span></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.49111em;"><span class="" style="top: -2.314em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">q</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.740108em;"><span class="" style="top: -2.989em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span></span></span><span class="" style="top: -3.677em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">q</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.814108em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span></span></span></span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.88044em;"><span class=""></span></span></span></span></span><span class="mclose delimcenter" style="top: 0em;"><span class="delimsizing size3">)</span></span></span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 2.40003em; vertical-align: -0.95003em;"></span><span class="mord"><span class="mopen delimcenter" style="top: 0em;"><span class="delimsizing size3">(</span></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.32144em;"><span class="" style="top: -2.314em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord">0</span></span></span><span class="" style="top: -3.677em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.88044em;"><span class=""></span></span></span></span></span><span class="mclose delimcenter" style="top: 0em;"><span class="delimsizing size3">)</span></span></span><span class="mord"><span class="mopen delimcenter" style="top: 0em;"><span class="delimsizing size3">(</span></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.32144em;"><span class="" style="top: -2.314em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord">0</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord">1</span></span></span><span class="" style="top: -3.677em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.88044em;"><span class=""></span></span></span></span></span><span class="mclose delimcenter" style="top: 0em;"><span class="delimsizing size3">)</span></span></span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 2.40003em; vertical-align: -0.95003em;"></span><span class="mord"><span class="mopen delimcenter" style="top: 0em;"><span class="delimsizing size3">(</span></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.32144em;"><span class="" style="top: -2.314em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord">1</span></span></span><span class="" style="top: -3.677em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.88044em;"><span class=""></span></span></span></span></span><span class="mclose delimcenter" style="top: 0em;"><span class="delimsizing size3">)</span></span></span></span></span></span></span></span><br> 同理我们可以得到<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    (
   
   
    
     
      k
     
     
      1
     
    
    
     
      k
     
     
      2
     
    
   
   
    )
   
  
  
   \binom{k^1}{k^2}
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.41793em; vertical-align: -0.35001em;"></span><span class="mord"><span class="mopen delimcenter" style="top: 0em;"><span class="delimsizing size1">(</span></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.06792em;"><span class="" style="top: -2.355em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.746314em;"><span class="" style="top: -2.786em; margin-right: 0.0714286em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span></span></span></span><span class="" style="top: -3.144em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.891314em;"><span class="" style="top: -2.931em; margin-right: 0.0714286em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mtight">1</span></span></span></span></span></span></span></span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.345em;"><span class=""></span></span></span></span></span><span class="mclose delimcenter" style="top: 0em;"><span class="delimsizing size1">)</span></span></span></span></span></span></span>和<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    (
   
   
    
     
      v
     
     
      1
     
    
    
     
      v
     
     
      2
     
    
   
   
    )
   
  
  
   \binom{v^1}{v^2}
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.41793em; vertical-align: -0.35001em;"></span><span class="mord"><span class="mopen delimcenter" style="top: 0em;"><span class="delimsizing size1">(</span></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.06792em;"><span class="" style="top: -2.355em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight"><span style="margin-right: 0.03588em;" class="mord mathdefault mtight">v</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.746314em;"><span class="" style="top: -2.786em; margin-right: 0.0714286em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span></span></span></span><span class="" style="top: -3.144em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight"><span style="margin-right: 0.03588em;" class="mord mathdefault mtight">v</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.891314em;"><span class="" style="top: -2.931em; margin-right: 0.0714286em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mtight">1</span></span></span></span></span></span></span></span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.345em;"><span class=""></span></span></span></span></span><span class="mclose delimcenter" style="top: 0em;"><span class="delimsizing size1">)</span></span></span></span></span></span></span>，那么求得的<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    (
   
   
    
     
      q
     
     
      1
     
    
    
     
      q
     
     
      2
     
    
   
   
    )
   
  
  
   \binom{q^1}{q^2}
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.54903em; vertical-align: -0.481108em;"></span><span class="mord"><span class="mopen delimcenter" style="top: 0em;"><span class="delimsizing size1">(</span></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.06792em;"><span class="" style="top: -2.355em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight"><span style="margin-right: 0.03588em;" class="mord mathdefault mtight">q</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.746314em;"><span class="" style="top: -2.786em; margin-right: 0.0714286em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span></span></span></span><span class="" style="top: -3.144em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight"><span style="margin-right: 0.03588em;" class="mord mathdefault mtight">q</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.891314em;"><span class="" style="top: -2.931em; margin-right: 0.0714286em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mtight">1</span></span></span></span></span></span></span></span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.481108em;"><span class=""></span></span></span></span></span><span class="mclose delimcenter" style="top: 0em;"><span class="delimsizing size1">)</span></span></span></span></span></span></span>就是原论文中的<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    Q
   
  
  
   Q
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.87777em; vertical-align: -0.19444em;"></span><span class="mord mathdefault">Q</span></span></span></span></span>，<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    (
   
   
    
     
      k
     
     
      1
     
    
    
     
      k
     
     
      2
     
    
   
   
    )
   
  
  
   \binom{k^1}{k^2}
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.41793em; vertical-align: -0.35001em;"></span><span class="mord"><span class="mopen delimcenter" style="top: 0em;"><span class="delimsizing size1">(</span></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.06792em;"><span class="" style="top: -2.355em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.746314em;"><span class="" style="top: -2.786em; margin-right: 0.0714286em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span></span></span></span><span class="" style="top: -3.144em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.891314em;"><span class="" style="top: -2.931em; margin-right: 0.0714286em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mtight">1</span></span></span></span></span></span></span></span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.345em;"><span class=""></span></span></span></span></span><span class="mclose delimcenter" style="top: 0em;"><span class="delimsizing size1">)</span></span></span></span></span></span></span>就是<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    K
   
  
  
   K
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span style="margin-right: 0.07153em;" class="mord mathdefault">K</span></span></span></span></span>，<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    (
   
   
    
     
      v
     
     
      1
     
    
    
     
      v
     
     
      2
     
    
   
   
    )
   
  
  
   \binom{v^1}{v^2}
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.41793em; vertical-align: -0.35001em;"></span><span class="mord"><span class="mopen delimcenter" style="top: 0em;"><span class="delimsizing size1">(</span></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.06792em;"><span class="" style="top: -2.355em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight"><span style="margin-right: 0.03588em;" class="mord mathdefault mtight">v</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.746314em;"><span class="" style="top: -2.786em; margin-right: 0.0714286em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span></span></span></span><span class="" style="top: -3.144em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight"><span style="margin-right: 0.03588em;" class="mord mathdefault mtight">v</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.891314em;"><span class="" style="top: -2.931em; margin-right: 0.0714286em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mtight">1</span></span></span></span></span></span></span></span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.345em;"><span class=""></span></span></span></span></span><span class="mclose delimcenter" style="top: 0em;"><span class="delimsizing size1">)</span></span></span></span></span></span></span>就是<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    V
   
  
  
   V
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span style="margin-right: 0.22222em;" class="mord mathdefault">V</span></span></span></span></span>。接着先拿<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     q
    
    
     1
    
   
  
  
   q^1
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.00855em; vertical-align: -0.19444em;"></span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">q</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.814108em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span></span></span></span></span></span></span></span></span>和每个<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    k
   
  
  
   k
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.69444em; vertical-align: 0em;"></span><span style="margin-right: 0.03148em;" class="mord mathdefault">k</span></span></span></span></span>进行match，点乘操作，接着除以<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     d
    
   
  
  
   \sqrt{d}
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.04em; vertical-align: -0.10778em;"></span><span class="mord sqrt"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.93222em;"><span class="svg-align" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="mord" style="padding-left: 0.833em;"><span class="mord mathdefault">d</span></span></span><span class="" style="top: -2.89222em;"><span class="pstrut" style="height: 3em;"></span><span class="hide-tail" style="min-width: 0.853em; height: 1.08em;">
       <svg width="400em" height="1.08em" viewBox="0 0 400000 1080" preserveAspectRatio="xMinYMin slice">
        <path d="M95,702c-2.7,0,-7.17,-2.7,-13.5,-8c-5.8,-5.3,-9.5,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
558
559
560
561
562
563
564
565
566
567
568
569
570
571
572
573
574
575
576
577
578
579
580
581
582
583
584
585
586
587
588
589
590
591
592
593
594
595
596
597
598
599
600
601
602
603
604
605
606
607
608
609
610
611
612
613
614
615
616
617
618
619
620
621
622
623
624
625
626
627
628
629
630
631
632
633
634
635
636
637
638
639
640
641
642
643
644
645
646
647
648
649
650
651
652
653
654
655

-10,-9.5,-14c0,-2,0.3,-3.3,1,-4c1.3,-2.7,23.83,-20.7,67.5,-54c44.2,-33.3,65.8,
-50.3,66.5,-51c1.3,-1.3,3,-2,5,-2c4.7,0,8.7,3.3,12,10s173,378,173,378c0.7,0,
35.3,-71,104,-213c68.7,-142,137.5,-285,206.5,-429c69,-144,104.5,-217.7,106.5,
-221c5.3,-9.3,12,-14,20,-14H400000v40H845.2724s-225.272,467,-225.272,467
s-235,486,-235,486c-2.7,4.7,-9,7,-19,7c-6,0,-10,-1,-12,-3s-194,-422,-194,-422
s-65,47,-65,47z M834 80H400000v40H845z">
得到对应的

    α
   
  
  
   \alpha
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.43056em; vertical-align: 0em;"></span><span style="margin-right: 0.0037em;" class="mord mathdefault">α</span></span></span></span></span>，其中<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    d
   
  
  
   d
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.69444em; vertical-align: 0em;"></span><span class="mord mathdefault">d</span></span></span></span></span>代表向量<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     k
    
    
     i
    
   
  
  
   k^i
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.824664em; vertical-align: 0em;"></span><span class="mord"><span style="margin-right: 0.03148em;" class="mord mathdefault">k</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.824664em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span></span></span></span></span></span></span></span></span></span>的长度，在本示例中等于2，除以<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     d
    
   
  
  
   \sqrt{d}
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.04em; vertical-align: -0.10778em;"></span><span class="mord sqrt"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.93222em;"><span class="svg-align" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="mord" style="padding-left: 0.833em;"><span class="mord mathdefault">d</span></span></span><span class="" style="top: -2.89222em;"><span class="pstrut" style="height: 3em;"></span><span class="hide-tail" style="min-width: 0.853em; height: 1.08em;">
       <svg width="400em" height="1.08em" viewBox="0 0 400000 1080" preserveAspectRatio="xMinYMin slice">
        <path d="M95,702c-2.7,0,-7.17,-2.7,-13.5,-8c-5.8,-5.3,-9.5,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

     d
    
   
  
  
   \sqrt{d}
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.04em; vertical-align: -0.10778em;"></span><span class="mord sqrt"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.93222em;"><span class="svg-align" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="mord" style="padding-left: 0.833em;"><span class="mord mathdefault">d</span></span></span><span class="" style="top: -2.89222em;"><span class="pstrut" style="height: 3em;"></span><span class="hide-tail" style="min-width: 0.853em; height: 1.08em;">
       <svg width="400em" height="1.08em" viewBox="0 0 400000 1080" preserveAspectRatio="xMinYMin slice">
        <path d="M95,702c-2.7,0,-7.17,-2.7,-13.5,-8c-5.8,-5.3,-9.5,
1
2
3
4
5
6
7
8
9
10
11

     α
    
    
     
      1
     
     
      ,
     
     
      i
     
    
   
  
  
   \alpha_{1, i}
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.716668em; vertical-align: -0.286108em;"></span><span class="mord"><span style="margin-right: 0.0037em;" class="mord mathdefault">α</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: -0.0037em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span><span class="mpunct mtight">,</span><span class="mord mathdefault mtight">i</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span></span></span></span></span>：<br> <span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
 
  
   
    
     
      α
     
     
      
       1
      
      
       ,
      
      
       1
      
     
    
    
     =
    
    
     
      
       
        q
       
       
        1
       
      
      
       ⋅
      
      
       
        k
       
       
        1
       
      
     
     
      
       d
      
     
    
    
     =
    
    
     
      
       1
      
      
       ×
      
      
       1
      
      
       +
      
      
       2
      
      
       ×
      
      
       0
      
     
     
      
       2
      
     
    
    
     =
    
    
     0.71
    
    
    
     
      α
     
     
      
       1
      
      
       ,
      
      
       2
      
     
    
    
     =
    
    
     
      
       
        q
       
       
        1
       
      
      
       ⋅
      
      
       
        k
       
       
        2
       
      
     
     
      
       d
      
     
    
    
     =
    
    
     
      
       1
      
      
       ×
      
      
       0
      
      
       +
      
      
       2
      
      
       ×
      
      
       1
      
     
     
      
       2
      
     
    
    
     =
    
    
     1.41
    
   
   
     \alpha_{1, 1} = \frac{q^1 \cdot k^1}{\sqrt{d}}=\frac{1\times 1+2\times 0}{\sqrt{2}}=0.71 \\ \alpha_{1, 2} = \frac{q^1 \cdot k^2}{\sqrt{d}}=\frac{1\times 0+2\times 1}{\sqrt{2}}=1.41 
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.716668em; vertical-align: -0.286108em;"></span><span class="mord"><span style="margin-right: 0.0037em;" class="mord mathdefault">α</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: -0.0037em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span><span class="mpunct mtight">,</span><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 2.42111em; vertical-align: -0.93em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.49111em;"><span class="" style="top: -2.17778em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord sqrt"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.93222em;"><span class="svg-align" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="mord" style="padding-left: 0.833em;"><span class="mord mathdefault">d</span></span></span><span class="" style="top: -2.89222em;"><span class="pstrut" style="height: 3em;"></span><span class="hide-tail" style="min-width: 0.853em; height: 1.08em;">
               <svg width="400em" height="1.08em" viewBox="0 0 400000 1080" preserveAspectRatio="xMinYMin slice">
                <path d="M95,702c-2.7,0,-7.17,-2.7,-13.5,-8c-5.8,-5.3,-9.5,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204

     q
    
    
     2
    
   
  
  
   q^2
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.00855em; vertical-align: -0.19444em;"></span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">q</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.814108em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span></span></span></span></span>去匹配所有的<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    k
   
  
  
   k
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.69444em; vertical-align: 0em;"></span><span style="margin-right: 0.03148em;" class="mord mathdefault">k</span></span></span></span></span>能得到<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     α
    
    
     
      2
     
     
      ,
     
     
      i
     
    
   
  
  
   \alpha_{2, i}
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.716668em; vertical-align: -0.286108em;"></span><span class="mord"><span style="margin-right: 0.0037em;" class="mord mathdefault">α</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: -0.0037em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">2</span><span class="mpunct mtight">,</span><span class="mord mathdefault mtight">i</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span></span></span></span></span>，统一写成矩阵乘法形式：<br> <span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
 
  
   
    
     
      (
     
     
      
       
        
         α
        
        
         
          1
         
         
          ,
         
         
          1
         
        
       
       
        &nbsp;&nbsp;
       
       
        
         α
        
        
         
          1
         
         
          ,
         
         
          2
         
        
       
      
      
       
        
         α
        
        
         
          2
         
         
          ,
         
         
          1
         
        
       
       
        &nbsp;&nbsp;
       
       
        
         α
        
        
         
          2
         
         
          ,
         
         
          2
         
        
       
      
     
     
      )
     
    
    
     =
    
    
     
      
       
        (
       
       
        
         
          q
         
         
          1
         
        
        
         
          q
         
         
          2
         
        
       
       
        )
       
      
      
       
        
         (
        
        
         
          
           k
          
          
           1
          
         
         
          
           k
          
          
           2
          
         
        
        
         )
        
       
       
        T
       
      
     
     
      
       d
      
     
    
   
   
     \binom{\alpha_{1, 1} \ \ \alpha_{1, 2}}{\alpha_{2, 1} \ \ \alpha_{2, 2}}=\frac{\binom{q^1}{q^2}\binom{k^1}{k^2}^T}{\sqrt{d}} 
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 2.42211em; vertical-align: -0.972108em;"></span><span class="mord"><span class="mopen delimcenter" style="top: 0em;"><span class="delimsizing size3">(</span></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.10756em;"><span class="" style="top: -2.314em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord"><span style="margin-right: 0.0037em;" class="mord mathdefault">α</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: -0.0037em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">2</span><span class="mpunct mtight">,</span><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mspace">&nbsp;</span><span class="mspace">&nbsp;</span><span class="mord"><span style="margin-right: 0.0037em;" class="mord mathdefault">α</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: -0.0037em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">2</span><span class="mpunct mtight">,</span><span class="mord mtight">2</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span></span></span><span class="" style="top: -3.677em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord"><span style="margin-right: 0.0037em;" class="mord mathdefault">α</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: -0.0037em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span><span class="mpunct mtight">,</span><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mspace">&nbsp;</span><span class="mspace">&nbsp;</span><span class="mord"><span style="margin-right: 0.0037em;" class="mord mathdefault">α</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: -0.0037em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span><span class="mpunct mtight">,</span><span class="mord mtight">2</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.972108em;"><span class=""></span></span></span></span></span><span class="mclose delimcenter" style="top: 0em;"><span class="delimsizing size3">)</span></span></span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 3.10026em; vertical-align: -0.93em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 2.17026em;"><span class="" style="top: -2.47693em;"><span class="pstrut" style="height: 3.29915em;"></span><span class="mord"><span class="mord sqrt"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.93222em;"><span class="svg-align" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="mord" style="padding-left: 0.833em;"><span class="mord mathdefault">d</span></span></span><span class="" style="top: -2.89222em;"><span class="pstrut" style="height: 3em;"></span><span class="hide-tail" style="min-width: 0.853em; height: 1.08em;">
               <svg width="400em" height="1.08em" viewBox="0 0 400000 1080" preserveAspectRatio="xMinYMin slice">
                <path d="M95,702c-2.7,0,-7.17,-2.7,-13.5,-8c-5.8,-5.3,-9.5,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213

    (
   
   
    
     α
    
    
     
      1
     
     
      ,
     
     
      1
     
    
   
   
    ,
   
   
    
     α
    
    
     
      1
     
     
      ,
     
     
      2
     
    
   
   
    )
   
  
  
   (\alpha_{1, 1}, \alpha_{1, 2})
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.03611em; vertical-align: -0.286108em;"></span><span class="mopen">(</span><span class="mord"><span style="margin-right: 0.0037em;" class="mord mathdefault">α</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: -0.0037em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span><span class="mpunct mtight">,</span><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span style="margin-right: 0.0037em;" class="mord mathdefault">α</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: -0.0037em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span><span class="mpunct mtight">,</span><span class="mord mtight">2</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mclose">)</span></span></span></span></span>和<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    (
   
   
    
     α
    
    
     
      2
     
     
      ,
     
     
      1
     
    
   
   
    ,
   
   
    
     α
    
    
     
      2
     
     
      ,
     
     
      2
     
    
   
   
    )
   
  
  
   (\alpha_{2, 1}, \alpha_{2, 2})
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.03611em; vertical-align: -0.286108em;"></span><span class="mopen">(</span><span class="mord"><span style="margin-right: 0.0037em;" class="mord mathdefault">α</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: -0.0037em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">2</span><span class="mpunct mtight">,</span><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span style="margin-right: 0.0037em;" class="mord mathdefault">α</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: -0.0037em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">2</span><span class="mpunct mtight">,</span><span class="mord mtight">2</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mclose">)</span></span></span></span></span>分别进行softmax处理得到<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    (
   
   
    
     
      α
     
     
      ^
     
    
    
     
      1
     
     
      ,
     
     
      1
     
    
   
   
    ,
   
   
    
     
      α
     
     
      ^
     
    
    
     
      1
     
     
      ,
     
     
      2
     
    
   
   
    )
   
  
  
   (\hat\alpha_{1, 1}, \hat\alpha_{1, 2})
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.03611em; vertical-align: -0.286108em;"></span><span class="mopen">(</span><span class="mord"><span class="mord accent"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.69444em;"><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span style="margin-right: 0.0037em;" class="mord mathdefault">α</span></span><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="accent-body" style="left: -0.22222em;">^</span></span></span></span></span></span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: -0.0037em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span><span class="mpunct mtight">,</span><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span class="mord accent"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.69444em;"><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span style="margin-right: 0.0037em;" class="mord mathdefault">α</span></span><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="accent-body" style="left: -0.22222em;">^</span></span></span></span></span></span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: -0.0037em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span><span class="mpunct mtight">,</span><span class="mord mtight">2</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mclose">)</span></span></span></span></span>和<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    (
   
   
    
     
      α
     
     
      ^
     
    
    
     
      2
     
     
      ,
     
     
      1
     
    
   
   
    ,
   
   
    
     
      α
     
     
      ^
     
    
    
     
      2
     
     
      ,
     
     
      2
     
    
   
   
    )
   
  
  
   (\hat\alpha_{2, 1}, \hat\alpha_{2, 2})
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.03611em; vertical-align: -0.286108em;"></span><span class="mopen">(</span><span class="mord"><span class="mord accent"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.69444em;"><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span style="margin-right: 0.0037em;" class="mord mathdefault">α</span></span><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="accent-body" style="left: -0.22222em;">^</span></span></span></span></span></span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: -0.0037em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">2</span><span class="mpunct mtight">,</span><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span class="mord accent"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.69444em;"><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span style="margin-right: 0.0037em;" class="mord mathdefault">α</span></span><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="accent-body" style="left: -0.22222em;">^</span></span></span></span></span></span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: -0.0037em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">2</span><span class="mpunct mtight">,</span><span class="mord mtight">2</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mclose">)</span></span></span></span></span>，这里的<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     α
    
    
     ^
    
   
  
  
   \hat{\alpha}
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.69444em; vertical-align: 0em;"></span><span class="mord accent"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.69444em;"><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span style="margin-right: 0.0037em;" class="mord mathdefault">α</span></span></span><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="accent-body" style="left: -0.22222em;">^</span></span></span></span></span></span></span></span></span></span>相当于计算得到针对每个<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    v
   
  
  
   v
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.43056em; vertical-align: 0em;"></span><span style="margin-right: 0.03588em;" class="mord mathdefault">v</span></span></span></span></span>的权重。到这我们就完成了<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     A
    
    
     t
    
    
     t
    
    
     e
    
    
     n
    
    
     t
    
    
     i
    
    
     o
    
    
     n
    
   
   
    (
   
   
    Q
   
   
    ,
   
   
    K
   
   
    ,
   
   
    V
   
   
    )
   
  
  
   {\rm Attention}(Q, K, V)
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord"><span class="mord"><span class="mord mathrm">A</span><span class="mord mathrm">t</span><span class="mord mathrm">t</span><span class="mord mathrm">e</span><span class="mord mathrm">n</span><span class="mord mathrm">t</span><span class="mord mathrm">i</span><span class="mord mathrm">o</span><span class="mord mathrm">n</span></span></span><span class="mopen">(</span><span class="mord mathdefault">Q</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span style="margin-right: 0.07153em;" class="mord mathdefault">K</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span style="margin-right: 0.22222em;" class="mord mathdefault">V</span><span class="mclose">)</span></span></span></span></span>公式中<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     s
    
    
     o
    
    
     f
    
    
     t
    
    
     m
    
    
     a
    
    
     x
    
   
   
    (
   
   
    
     
      Q
     
     
      
       K
      
      
       T
      
     
    
    
     
      
       d
      
      
       k
      
     
    
   
   
    )
   
  
  
   {\rm softmax}(\frac{QK^T}{\sqrt{d_k}})
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.62747em; vertical-align: -0.538em;"></span><span class="mord"><span class="mord"><span class="mord mathrm">s</span><span class="mord mathrm">o</span><span style="margin-right: 0.07778em;" class="mord mathrm">f</span><span class="mord mathrm">t</span><span class="mord mathrm">m</span><span class="mord mathrm">a</span><span class="mord mathrm">x</span></span></span><span class="mopen">(</span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.08947em;"><span class="" style="top: -2.58644em;"><span class="pstrut" style="height: 3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord sqrt mtight"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.862231em;"><span class="svg-align" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="mord mtight" style="padding-left: 0.833em;"><span class="mord mtight"><span class="mord mathdefault mtight">d</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3448em;"><span class="" style="top: -2.34877em; margin-left: 0em; margin-right: 0.0714286em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.151229em;"><span class=""></span></span></span></span></span></span></span></span><span class="" style="top: -2.82223em;"><span class="pstrut" style="height: 3em;"></span><span class="hide-tail mtight" style="min-width: 0.853em; height: 1.08em;">
               <svg width="400em" height="1.08em" viewBox="0 0 400000 1080" preserveAspectRatio="xMinYMin slice">
                <path d="M95,702c-2.7,0,-7.17,-2.7,-13.5,-8c-5.8,-5.3,-9.5,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369

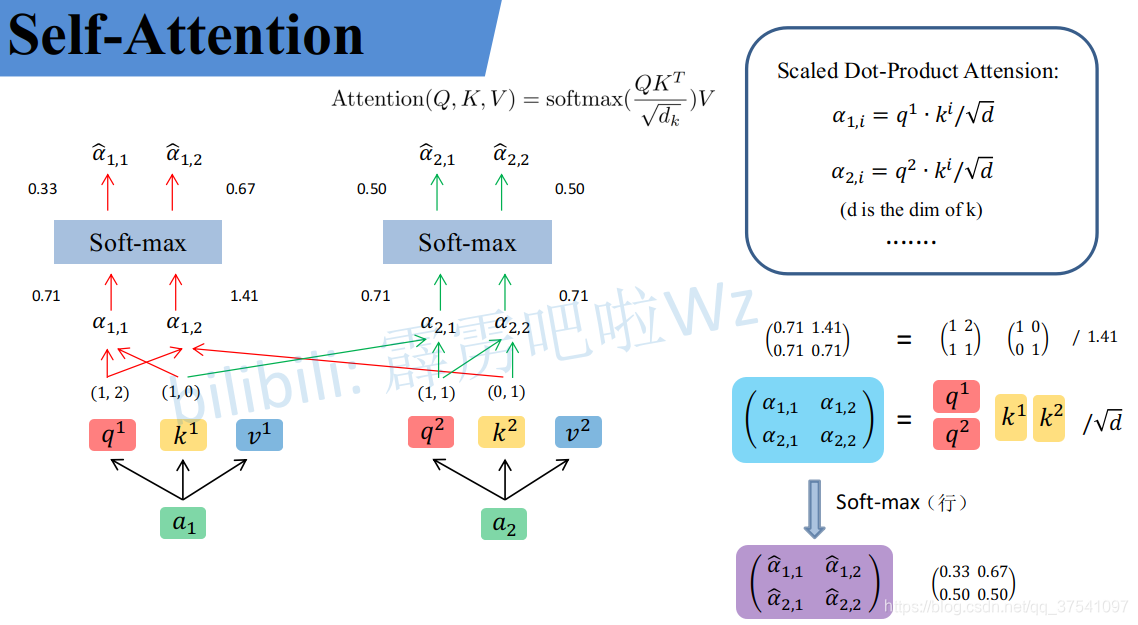
self-attention
上面已经计算得到

    α
   
  
  
   \alpha
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.43056em; vertical-align: 0em;"></span><span style="margin-right: 0.0037em;" class="mord mathdefault">α</span></span></span></span></span>，即针对每个<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    v
   
  
  
   v
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.43056em; vertical-align: 0em;"></span><span style="margin-right: 0.03588em;" class="mord mathdefault">v</span></span></span></span></span>的权重，接着进行加权得到最终结果：<br> <span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
 
  
   
    
     
      b
     
     
      1
     
    
    
     =
    
    
     
      
       α
      
      
       ^
      
     
     
      
       1
      
      
       ,
      
      
       1
      
     
    
    
     ×
    
    
     
      v
     
     
      1
     
    
    
     +
    
    
     
      
       α
      
      
       ^
      
     
     
      
       1
      
      
       ,
      
      
       2
      
     
    
    
     ×
    
    
     
      v
     
     
      2
     
    
    
     =
    
    
     (
    
    
     0.33
    
    
     ,
    
    
     0.67
    
    
     )
    
    
    
     
      b
     
     
      2
     
    
    
     =
    
    
     
      
       α
      
      
       ^
      
     
     
      
       2
      
      
       ,
      
      
       1
      
     
    
    
     ×
    
    
     
      v
     
     
      1
     
    
    
     +
    
    
     
      
       α
      
      
       ^
      
     
     
      
       2
      
      
       ,
      
      
       2
      
     
    
    
     ×
    
    
     
      v
     
     
      2
     
    
    
     =
    
    
     (
    
    
     0.50
    
    
     ,
    
    
     0.50
    
    
     )
    
   
   
     b_1 = \hat{\alpha}_{1, 1} \times v^1 + \hat{\alpha}_{1, 2} \times v^2=(0.33, 0.67) \\ b_2 = \hat{\alpha}_{2, 1} \times v^1 + \hat{\alpha}_{2, 2} \times v^2=(0.50, 0.50) 
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.84444em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathdefault">b</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 0.980548em; vertical-align: -0.286108em;"></span><span class="mord"><span class="mord accent"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.69444em;"><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span style="margin-right: 0.0037em;" class="mord mathdefault">α</span></span></span><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="accent-body" style="left: -0.22222em;">^</span></span></span></span></span></span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span><span class="mpunct mtight">,</span><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.222222em;"></span><span class="mbin">×</span><span class="mspace" style="margin-right: 0.222222em;"></span></span><span class="base"><span class="strut" style="height: 0.947438em; vertical-align: -0.08333em;"></span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">v</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.864108em;"><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.222222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.222222em;"></span></span><span class="base"><span class="strut" style="height: 0.980548em; vertical-align: -0.286108em;"></span><span class="mord"><span class="mord accent"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.69444em;"><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span style="margin-right: 0.0037em;" class="mord mathdefault">α</span></span></span><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="accent-body" style="left: -0.22222em;">^</span></span></span></span></span></span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span><span class="mpunct mtight">,</span><span class="mord mtight">2</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.222222em;"></span><span class="mbin">×</span><span class="mspace" style="margin-right: 0.222222em;"></span></span><span class="base"><span class="strut" style="height: 0.864108em; vertical-align: 0em;"></span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">v</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.864108em;"><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span class="mord">0</span><span class="mord">.</span><span class="mord">3</span><span class="mord">3</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord">0</span><span class="mord">.</span><span class="mord">6</span><span class="mord">7</span><span class="mclose">)</span></span><span class="mspace newline"></span><span class="base"><span class="strut" style="height: 0.84444em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathdefault">b</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 0.980548em; vertical-align: -0.286108em;"></span><span class="mord"><span class="mord accent"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.69444em;"><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span style="margin-right: 0.0037em;" class="mord mathdefault">α</span></span></span><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="accent-body" style="left: -0.22222em;">^</span></span></span></span></span></span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">2</span><span class="mpunct mtight">,</span><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.222222em;"></span><span class="mbin">×</span><span class="mspace" style="margin-right: 0.222222em;"></span></span><span class="base"><span class="strut" style="height: 0.947438em; vertical-align: -0.08333em;"></span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">v</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.864108em;"><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.222222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.222222em;"></span></span><span class="base"><span class="strut" style="height: 0.980548em; vertical-align: -0.286108em;"></span><span class="mord"><span class="mord accent"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.69444em;"><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span style="margin-right: 0.0037em;" class="mord mathdefault">α</span></span></span><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="accent-body" style="left: -0.22222em;">^</span></span></span></span></span></span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">2</span><span class="mpunct mtight">,</span><span class="mord mtight">2</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.222222em;"></span><span class="mbin">×</span><span class="mspace" style="margin-right: 0.222222em;"></span></span><span class="base"><span class="strut" style="height: 0.864108em; vertical-align: 0em;"></span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">v</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.864108em;"><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span class="mord">0</span><span class="mord">.</span><span class="mord">5</span><span class="mord">0</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord">0</span><span class="mord">.</span><span class="mord">5</span><span class="mord">0</span><span class="mclose">)</span></span></span></span></span></span><br> 统一写成矩阵乘法形式：<br> <span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
 
  
   
    
     
      (
     
     
      
       
        b
       
       
        1
       
      
      
       
        b
       
       
        2
       
      
     
     
      )
     
    
    
     =
    
    
     
      (
     
     
      
       
        
         
          α
         
         
          ^
         
        
        
         
          1
         
         
          ,
         
         
          1
         
        
       
       
        &nbsp;&nbsp;
       
       
        
         
          α
         
         
          ^
         
        
        
         
          1
         
         
          ,
         
         
          2
         
        
       
      
      
       
        
         
          α
         
         
          ^
         
        
        
         
          2
         
         
          ,
         
         
          1
         
        
       
       
        &nbsp;&nbsp;
       
       
        
         
          α
         
         
          ^
         
        
        
         
          2
         
         
          ,
         
         
          2
         
        
       
      
     
     
      )
     
    
    
     
      (
     
     
      
       
        v
       
       
        1
       
      
      
       
        v
       
       
        2
       
      
     
     
      )
     
    
   
   
     \binom{b_1}{b_2} = \binom{\hat\alpha_{1, 1} \ \ \hat\alpha_{1, 2}}{\hat\alpha_{2, 1} \ \ \hat\alpha_{2, 2}}\binom{v^1}{v^2} 
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 2.40003em; vertical-align: -0.95003em;"></span><span class="mord"><span class="mopen delimcenter" style="top: 0em;"><span class="delimsizing size3">(</span></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.37144em;"><span class="" style="top: -2.314em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord"><span class="mord mathdefault">b</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span><span class="" style="top: -3.677em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord"><span class="mord mathdefault">b</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.836em;"><span class=""></span></span></span></span></span><span class="mclose delimcenter" style="top: 0em;"><span class="delimsizing size3">)</span></span></span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 2.46322em; vertical-align: -0.972108em;"></span><span class="mord"><span class="mopen delimcenter" style="top: 0em;"><span class="delimsizing size3">(</span></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.37144em;"><span class="" style="top: -2.314em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord"><span class="mord accent"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.69444em;"><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span style="margin-right: 0.0037em;" class="mord mathdefault">α</span></span><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="accent-body" style="left: -0.22222em;">^</span></span></span></span></span></span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: -0.0037em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">2</span><span class="mpunct mtight">,</span><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mspace">&nbsp;</span><span class="mspace">&nbsp;</span><span class="mord"><span class="mord accent"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.69444em;"><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span style="margin-right: 0.0037em;" class="mord mathdefault">α</span></span><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="accent-body" style="left: -0.22222em;">^</span></span></span></span></span></span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: -0.0037em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">2</span><span class="mpunct mtight">,</span><span class="mord mtight">2</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span></span></span><span class="" style="top: -3.677em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord"><span class="mord accent"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.69444em;"><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span style="margin-right: 0.0037em;" class="mord mathdefault">α</span></span><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="accent-body" style="left: -0.22222em;">^</span></span></span></span></span></span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: -0.0037em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span><span class="mpunct mtight">,</span><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mspace">&nbsp;</span><span class="mspace">&nbsp;</span><span class="mord"><span class="mord accent"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.69444em;"><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span style="margin-right: 0.0037em;" class="mord mathdefault">α</span></span><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="accent-body" style="left: -0.22222em;">^</span></span></span></span></span></span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: -0.0037em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span><span class="mpunct mtight">,</span><span class="mord mtight">2</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.972108em;"><span class=""></span></span></span></span></span><span class="mclose delimcenter" style="top: 0em;"><span class="delimsizing size3">)</span></span></span><span class="mord"><span class="mopen delimcenter" style="top: 0em;"><span class="delimsizing size3">(</span></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.49111em;"><span class="" style="top: -2.314em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">v</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.740108em;"><span class="" style="top: -2.989em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span></span></span><span class="" style="top: -3.677em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">v</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.814108em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span></span></span></span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.686em;"><span class=""></span></span></span></span></span><span class="mclose delimcenter" style="top: 0em;"><span class="delimsizing size3">)</span></span></span></span></span></span></span></span><br> <img src="https://img-blog.csdnimg.cn/2021060816151080.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzM3NTQxMDk3,size_16,color_FFFFFF,t_70#pic_center" alt="self-attention">到这，<code onclick="mdcp.copyCode(event)" style="user-select: auto;">Self-Attention</code>的内容就讲完了。总结下来就是论文中的一个公式：<br> <span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
 
  
   
    
     
      A
     
     
      t
     
     
      t
     
     
      e
     
     
      n
     
     
      t
     
     
      i
     
     
      o
     
     
      n
     
    
    
     (
    
    
     Q
    
    
     ,
    
    
     K
    
    
     ,
    
    
     V
    
    
     )
    
    
     =
    
    
     
      s
     
     
      o
     
     
      f
     
     
      t
     
     
      m
     
     
      a
     
     
      x
     
    
    
     (
    
    
     
      
       Q
      
      
       
        K
       
       
        T
       
      
     
     
      
       
        d
       
       
        k
       
      
     
    
    
     )
    
    
     V
    
   
   
     {\rm Attention}(Q, K, V)={\rm softmax}(\frac{QK^T}{\sqrt{d_k}})V 
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord"><span class="mord"><span class="mord mathrm">A</span><span class="mord mathrm">t</span><span class="mord mathrm">t</span><span class="mord mathrm">e</span><span class="mord mathrm">n</span><span class="mord mathrm">t</span><span class="mord mathrm">i</span><span class="mord mathrm">o</span><span class="mord mathrm">n</span></span></span><span class="mopen">(</span><span class="mord mathdefault">Q</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span style="margin-right: 0.07153em;" class="mord mathdefault">K</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span style="margin-right: 0.22222em;" class="mord mathdefault">V</span><span class="mclose">)</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 2.44833em; vertical-align: -0.93em;"></span><span class="mord"><span class="mord"><span class="mord mathrm">s</span><span class="mord mathrm">o</span><span style="margin-right: 0.07778em;" class="mord mathrm">f</span><span class="mord mathrm">t</span><span class="mord mathrm">m</span><span class="mord mathrm">a</span><span class="mord mathrm">x</span></span></span><span class="mopen">(</span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.51833em;"><span class="" style="top: -2.25278em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord sqrt"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.85722em;"><span class="svg-align" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="mord" style="padding-left: 0.833em;"><span class="mord"><span class="mord mathdefault">d</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.336108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span><span class="" style="top: -2.81722em;"><span class="pstrut" style="height: 3em;"></span><span class="hide-tail" style="min-width: 0.853em; height: 1.08em;">
               <svg width="400em" height="1.08em" viewBox="0 0 400000 1080" preserveAspectRatio="xMinYMin slice">
                <path d="M95,702c-2.7,0,-7.17,-2.7,-13.5,-8c-5.8,-5.3,-9.5,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511

Multi-Head Attention

刚刚已经聊完了Self-Attention模块，接下来再来看看Multi-Head Attention模块，实际使用中基本使用的还是Multi-Head Attention模块。原论文中说使用多头注意力机制能够联合来自不同head部分学习到的信息。Multi-head attention allows the model to jointly attend to information from different representation subspaces at different positions.其实只要懂了Self-Attention模块Multi-Head Attention模块就非常简单了。

首先还是和Self-Attention模块一样将

     a
    
    
     i
    
   
  
  
   a_i
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.58056em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathdefault">a</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>分别通过<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     W
    
    
     q
    
   
   
    ,
   
   
    
     W
    
    
     k
    
   
   
    ,
   
   
    
     W
    
    
     v
    
   
  
  
   W^q, W^k, W^v
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.04355em; vertical-align: -0.19444em;"></span><span class="mord"><span style="margin-right: 0.13889em;" class="mord mathdefault">W</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.664392em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span style="margin-right: 0.03588em;" class="mord mathdefault mtight">q</span></span></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span style="margin-right: 0.13889em;" class="mord mathdefault">W</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.849108em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span></span></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span style="margin-right: 0.13889em;" class="mord mathdefault">W</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.664392em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span style="margin-right: 0.03588em;" class="mord mathdefault mtight">v</span></span></span></span></span></span></span></span></span></span></span></span>得到对应的<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     q
    
    
     i
    
   
   
    ,
   
   
    
     k
    
    
     i
    
   
   
    ,
   
   
    
     v
    
    
     i
    
   
  
  
   q^i, k^i, v^i
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.0191em; vertical-align: -0.19444em;"></span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">q</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.824664em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span style="margin-right: 0.03148em;" class="mord mathdefault">k</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.824664em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">v</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.824664em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span></span></span></span></span></span></span></span></span></span>，然后再根据使用的head的数目<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    h
   
  
  
   h
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.69444em; vertical-align: 0em;"></span><span class="mord mathdefault">h</span></span></span></span></span>进一步把得到的<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     q
    
    
     i
    
   
   
    ,
   
   
    
     k
    
    
     i
    
   
   
    ,
   
   
    
     v
    
    
     i
    
   
  
  
   q^i, k^i, v^i
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.0191em; vertical-align: -0.19444em;"></span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">q</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.824664em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span style="margin-right: 0.03148em;" class="mord mathdefault">k</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.824664em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">v</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.824664em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span></span></span></span></span></span></span></span></span></span>均分成<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    h
   
  
  
   h
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.69444em; vertical-align: 0em;"></span><span class="mord mathdefault">h</span></span></span></span></span>份。比如下图中假设<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    h
   
   
    =
   
   
    2
   
  
  
   h=2
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.69444em; vertical-align: 0em;"></span><span class="mord mathdefault">h</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 0.64444em; vertical-align: 0em;"></span><span class="mord">2</span></span></span></span></span>然后<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     q
    
    
     1
    
   
  
  
   q^1
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.00855em; vertical-align: -0.19444em;"></span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">q</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.814108em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span></span></span></span></span></span></span></span></span>拆分成<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     q
    
    
     
      1
     
     
      ,
     
     
      1
     
    
   
  
  
   q^{1,1}
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.00855em; vertical-align: -0.19444em;"></span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">q</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.814108em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span><span class="mpunct mtight">,</span><span class="mord mtight">1</span></span></span></span></span></span></span></span></span></span></span></span></span>和<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     q
    
    
     
      1
     
     
      ,
     
     
      2
     
    
   
  
  
   q^{1,2}
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.00855em; vertical-align: -0.19444em;"></span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">q</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.814108em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span><span class="mpunct mtight">,</span><span class="mord mtight">2</span></span></span></span></span></span></span></span></span></span></span></span></span>，那么<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     q
    
    
     
      1
     
     
      ,
     
     
      1
     
    
   
  
  
   q^{1,1}
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.00855em; vertical-align: -0.19444em;"></span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">q</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.814108em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span><span class="mpunct mtight">,</span><span class="mord mtight">1</span></span></span></span></span></span></span></span></span></span></span></span></span>就属于head1，<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     q
    
    
     
      1
     
     
      ,
     
     
      2
     
    
   
  
  
   q^{1,2}
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.00855em; vertical-align: -0.19444em;"></span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">q</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.814108em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span><span class="mpunct mtight">,</span><span class="mord mtight">2</span></span></span></span></span></span></span></span></span></span></span></span></span>属于head2。</p> 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288

multi-head
看到这里，如果读过原论文的人肯定有疑问，论文中不是写的通过

     W
    
    
     i
    
    
     Q
    
   
   
    ,
   
   
    
     W
    
    
     i
    
    
     K
    
   
   
    ,
   
   
    
     W
    
    
     i
    
    
     V
    
   
  
  
   W^Q_i, W^K_i, W^V_i
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.2361em; vertical-align: -0.276864em;"></span><span class="mord"><span style="margin-right: 0.13889em;" class="mord mathdefault">W</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.959239em;"><span class="" style="top: -2.42314em; margin-left: -0.13889em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span><span class="" style="top: -3.18091em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">Q</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.276864em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span style="margin-right: 0.13889em;" class="mord mathdefault">W</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.841331em;"><span class="" style="top: -2.44134em; margin-left: -0.13889em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span style="margin-right: 0.07153em;" class="mord mathdefault mtight">K</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.258664em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span style="margin-right: 0.13889em;" class="mord mathdefault">W</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.841331em;"><span class="" style="top: -2.44134em; margin-left: -0.13889em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span style="margin-right: 0.22222em;" class="mord mathdefault mtight">V</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.258664em;"><span class=""></span></span></span></span></span></span></span></span></span></span>映射得到每个head的<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     Q
    
    
     i
    
   
   
    ,
   
   
    
     K
    
    
     i
    
   
   
    ,
   
   
    
     V
    
    
     i
    
   
  
  
   Q_i, K_i, V_i
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.87777em; vertical-align: -0.19444em;"></span><span class="mord"><span class="mord mathdefault">Q</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span style="margin-right: 0.07153em;" class="mord mathdefault">K</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: -0.07153em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span style="margin-right: 0.22222em;" class="mord mathdefault">V</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: -0.22222em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>吗：<br> <span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
 
  
   
    
     h
    
    
     e
    
    
     a
    
    
     
      d
     
     
      i
     
    
    
     =
    
    
     
      A
     
     
      t
     
     
      t
     
     
      e
     
     
      n
     
     
      t
     
     
      i
     
     
      o
     
     
      n
     
    
    
     (
    
    
     Q
    
    
     
      W
     
     
      i
     
     
      Q
     
    
    
     ,
    
    
     K
    
    
     
      W
     
     
      i
     
     
      K
     
    
    
     ,
    
    
     V
    
    
     
      W
     
     
      i
     
     
      V
     
    
    
     )
    
   
   
     head_i = {\rm Attention}(QW^Q_i, KW^K_i, VW^V_i) 
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.84444em; vertical-align: -0.15em;"></span><span class="mord mathdefault">h</span><span class="mord mathdefault">e</span><span class="mord mathdefault">a</span><span class="mord"><span class="mord mathdefault">d</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 1.2361em; vertical-align: -0.276864em;"></span><span class="mord"><span class="mord"><span class="mord mathrm">A</span><span class="mord mathrm">t</span><span class="mord mathrm">t</span><span class="mord mathrm">e</span><span class="mord mathrm">n</span><span class="mord mathrm">t</span><span class="mord mathrm">i</span><span class="mord mathrm">o</span><span class="mord mathrm">n</span></span></span><span class="mopen">(</span><span class="mord mathdefault">Q</span><span class="mord"><span style="margin-right: 0.13889em;" class="mord mathdefault">W</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.959239em;"><span class="" style="top: -2.42314em; margin-left: -0.13889em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span><span class="" style="top: -3.18091em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">Q</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.276864em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span style="margin-right: 0.07153em;" class="mord mathdefault">K</span><span class="mord"><span style="margin-right: 0.13889em;" class="mord mathdefault">W</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.891331em;"><span class="" style="top: -2.453em; margin-left: -0.13889em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span style="margin-right: 0.07153em;" class="mord mathdefault mtight">K</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.247em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span style="margin-right: 0.22222em;" class="mord mathdefault">V</span><span class="mord"><span style="margin-right: 0.13889em;" class="mord mathdefault">W</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.891331em;"><span class="" style="top: -2.453em; margin-left: -0.13889em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span style="margin-right: 0.22222em;" class="mord mathdefault mtight">V</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.247em;"><span class=""></span></span></span></span></span></span><span class="mclose">)</span></span></span></span></span></span><br> 但我在github上看的一些源码中就是简单的进行均分，其实也可以将<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     W
    
    
     i
    
    
     Q
    
   
   
    ,
   
   
    
     W
    
    
     i
    
    
     K
    
   
   
    ,
   
   
    
     W
    
    
     i
    
    
     V
    
   
  
  
   W^Q_i, W^K_i, W^V_i
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.2361em; vertical-align: -0.276864em;"></span><span class="mord"><span style="margin-right: 0.13889em;" class="mord mathdefault">W</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.959239em;"><span class="" style="top: -2.42314em; margin-left: -0.13889em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span><span class="" style="top: -3.18091em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">Q</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.276864em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span style="margin-right: 0.13889em;" class="mord mathdefault">W</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.841331em;"><span class="" style="top: -2.44134em; margin-left: -0.13889em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span style="margin-right: 0.07153em;" class="mord mathdefault mtight">K</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.258664em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span style="margin-right: 0.13889em;" class="mord mathdefault">W</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.841331em;"><span class="" style="top: -2.44134em; margin-left: -0.13889em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span style="margin-right: 0.22222em;" class="mord mathdefault mtight">V</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.258664em;"><span class=""></span></span></span></span></span></span></span></span></span></span>设置成对应值来实现均分，比如下图中的Q通过<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     W
    
    
     1
    
    
     Q
    
   
  
  
   W^Q_1
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.22555em; vertical-align: -0.266308em;"></span><span class="mord"><span style="margin-right: 0.13889em;" class="mord mathdefault">W</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.959239em;"><span class="" style="top: -2.43369em; margin-left: -0.13889em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span><span class="" style="top: -3.18091em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">Q</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.266308em;"><span class=""></span></span></span></span></span></span></span></span></span></span>就能得到均分后的<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     Q
    
    
     1
    
   
  
  
   Q_1
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.87777em; vertical-align: -0.19444em;"></span><span class="mord"><span class="mord mathdefault">Q</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>。</p> 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279

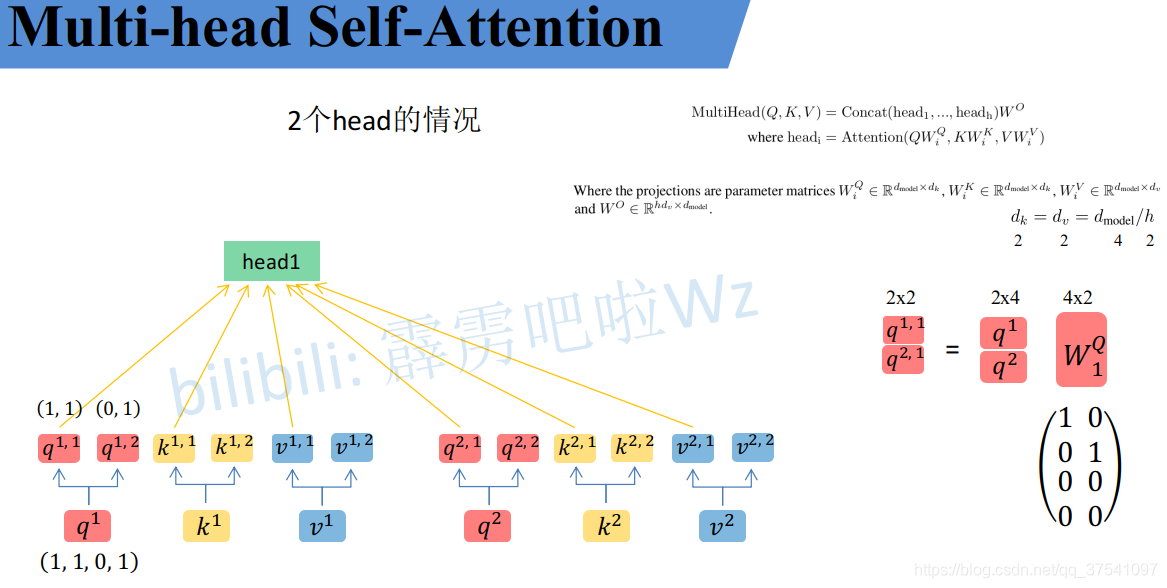
multi-head
通过上述方法就能得到每个

    h
   
   
    e
   
   
    a
   
   
    
     d
    
    
     i
    
   
  
  
   head_i
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.84444em; vertical-align: -0.15em;"></span><span class="mord mathdefault">h</span><span class="mord mathdefault">e</span><span class="mord mathdefault">a</span><span class="mord"><span class="mord mathdefault">d</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>对应的<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     Q
    
    
     i
    
   
   
    ,
   
   
    
     K
    
    
     i
    
   
   
    ,
   
   
    
     V
    
    
     i
    
   
  
  
   Q_i, K_i, V_i
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.87777em; vertical-align: -0.19444em;"></span><span class="mord"><span class="mord mathdefault">Q</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span style="margin-right: 0.07153em;" class="mord mathdefault">K</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: -0.07153em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span style="margin-right: 0.22222em;" class="mord mathdefault">V</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: -0.22222em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>参数，接下来针对每个head使用和Self-Attention中相同的方法即可得到对应的结果。<br> <span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
 
  
   
    
     
      A
     
     
      t
     
     
      t
     
     
      e
     
     
      n
     
     
      t
     
     
      i
     
     
      o
     
     
      n
     
    
    
     (
    
    
     
      Q
     
     
      i
     
    
    
     ,
    
    
     
      K
     
     
      i
     
    
    
     ,
    
    
     
      V
     
     
      i
     
    
    
     )
    
    
     =
    
    
     
      s
     
     
      o
     
     
      f
     
     
      t
     
     
      m
     
     
      a
     
     
      x
     
    
    
     (
    
    
     
      
       
        Q
       
       
        i
       
      
      
       
        K
       
       
        i
       
       
        T
       
      
     
     
      
       
        d
       
       
        k
       
      
     
    
    
     )
    
    
     
      V
     
     
      i
     
    
   
   
     {\rm Attention}(Q_i, K_i, V_i)={\rm softmax}(\frac{Q_iK_i^T}{\sqrt{d_k}})V_i 
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord"><span class="mord"><span class="mord mathrm">A</span><span class="mord mathrm">t</span><span class="mord mathrm">t</span><span class="mord mathrm">e</span><span class="mord mathrm">n</span><span class="mord mathrm">t</span><span class="mord mathrm">i</span><span class="mord mathrm">o</span><span class="mord mathrm">n</span></span></span><span class="mopen">(</span><span class="mord"><span class="mord mathdefault">Q</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span style="margin-right: 0.07153em;" class="mord mathdefault">K</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: -0.07153em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span style="margin-right: 0.22222em;" class="mord mathdefault">V</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: -0.22222em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mclose">)</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 2.44833em; vertical-align: -0.93em;"></span><span class="mord"><span class="mord"><span class="mord mathrm">s</span><span class="mord mathrm">o</span><span style="margin-right: 0.07778em;" class="mord mathrm">f</span><span class="mord mathrm">t</span><span class="mord mathrm">m</span><span class="mord mathrm">a</span><span class="mord mathrm">x</span></span></span><span class="mopen">(</span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.51833em;"><span class="" style="top: -2.25278em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord sqrt"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.85722em;"><span class="svg-align" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="mord" style="padding-left: 0.833em;"><span class="mord"><span class="mord mathdefault">d</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.336108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span><span class="" style="top: -2.81722em;"><span class="pstrut" style="height: 3em;"></span><span class="hide-tail" style="min-width: 0.853em; height: 1.08em;">
               <svg width="400em" height="1.08em" viewBox="0 0 400000 1080" preserveAspectRatio="xMinYMin slice">
                <path d="M95,702c-2.7,0,-7.17,-2.7,-13.5,-8c-5.8,-5.3,-9.5,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210

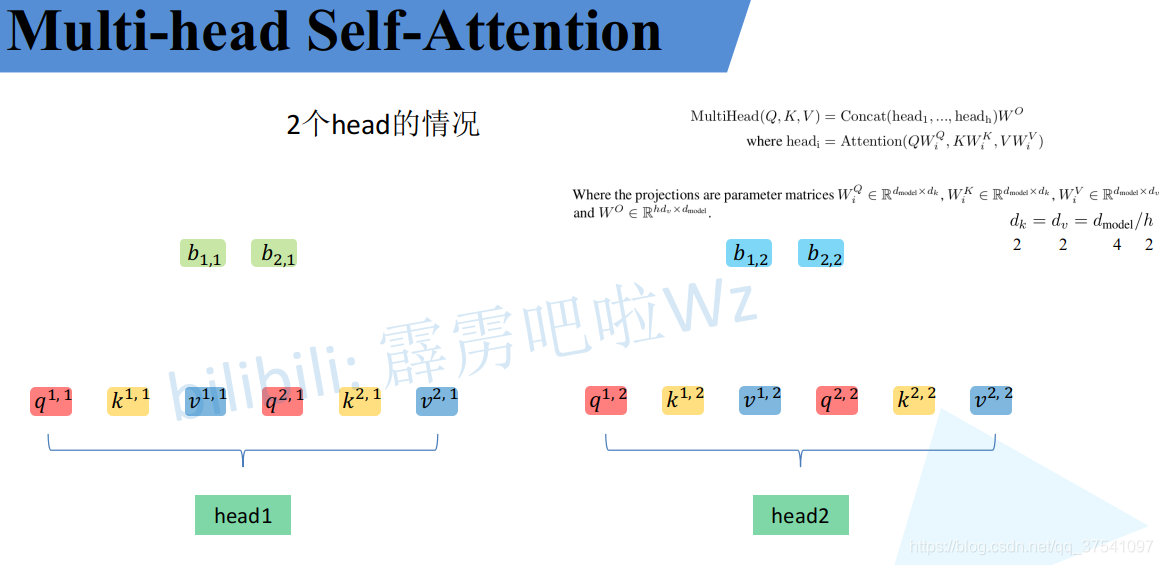
multi-head
接着将每个head得到的结果进行concat拼接，比如下图中

     b
    
    
     
      1
     
     
      ,
     
     
      1
     
    
   
  
  
   b_{1,1}
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.980548em; vertical-align: -0.286108em;"></span><span class="mord"><span class="mord mathdefault">b</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span><span class="mpunct mtight">,</span><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span></span></span></span></span>（<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    h
   
   
    e
   
   
    a
   
   
    
     d
    
    
     1
    
   
  
  
   head_1
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.84444em; vertical-align: -0.15em;"></span><span class="mord mathdefault">h</span><span class="mord mathdefault">e</span><span class="mord mathdefault">a</span><span class="mord"><span class="mord mathdefault">d</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>得到的<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     b
    
    
     1
    
   
  
  
   b_1
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.84444em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathdefault">b</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>）和<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     b
    
    
     
      1
     
     
      ,
     
     
      2
     
    
   
  
  
   b_{1,2}
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.980548em; vertical-align: -0.286108em;"></span><span class="mord"><span class="mord mathdefault">b</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span><span class="mpunct mtight">,</span><span class="mord mtight">2</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span></span></span></span></span>（<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    h
   
   
    e
   
   
    a
   
   
    
     d
    
    
     2
    
   
  
  
   head_2
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.84444em; vertical-align: -0.15em;"></span><span class="mord mathdefault">h</span><span class="mord mathdefault">e</span><span class="mord mathdefault">a</span><span class="mord"><span class="mord mathdefault">d</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>得到的<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     b
    
    
     1
    
   
  
  
   b_1
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.84444em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathdefault">b</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>）拼接在一起，<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     b
    
    
     
      2
     
     
      ,
     
     
      1
     
    
   
  
  
   b_{2,1}
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.980548em; vertical-align: -0.286108em;"></span><span class="mord"><span class="mord mathdefault">b</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">2</span><span class="mpunct mtight">,</span><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span></span></span></span></span>（<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    h
   
   
    e
   
   
    a
   
   
    
     d
    
    
     1
    
   
  
  
   head_1
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.84444em; vertical-align: -0.15em;"></span><span class="mord mathdefault">h</span><span class="mord mathdefault">e</span><span class="mord mathdefault">a</span><span class="mord"><span class="mord mathdefault">d</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>得到的<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     b
    
    
     2
    
   
  
  
   b_2
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.84444em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathdefault">b</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>）和<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     b
    
    
     
      2
     
     
      ,
     
     
      2
     
    
   
  
  
   b_{2,2}
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.980548em; vertical-align: -0.286108em;"></span><span class="mord"><span class="mord mathdefault">b</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">2</span><span class="mpunct mtight">,</span><span class="mord mtight">2</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span></span></span></span></span>（<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    h
   
   
    e
   
   
    a
   
   
    
     d
    
    
     2
    
   
  
  
   head_2
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.84444em; vertical-align: -0.15em;"></span><span class="mord mathdefault">h</span><span class="mord mathdefault">e</span><span class="mord mathdefault">a</span><span class="mord"><span class="mord mathdefault">d</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>得到的<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     b
    
    
     2
    
   
  
  
   b_2
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.84444em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathdefault">b</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>）拼接在一起。</p> 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267

multi-head
接着将拼接后的结果通过

     W
    
    
     O
    
   
  
  
   W^O
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.841331em; vertical-align: 0em;"></span><span class="mord"><span style="margin-right: 0.13889em;" class="mord mathdefault">W</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.841331em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span style="margin-right: 0.02778em;" class="mord mathdefault mtight">O</span></span></span></span></span></span></span></span></span></span></span></span>（可学习的参数）进行融合，如下图所示，融合后得到最终的结果<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     b
    
    
     1
    
   
   
    ,
   
   
    
     b
    
    
     2
    
   
  
  
   b_1, b_2
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.88888em; vertical-align: -0.19444em;"></span><span class="mord"><span class="mord mathdefault">b</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span class="mord mathdefault">b</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>。</p> 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

在这里插入图片描述
到这，Multi-Head Attention的内容就讲完了。总结下来就是论文中的两个公式：

      M
     
     
      u
     
     
      l
     
     
      t
     
     
      i
     
     
      H
     
     
      e
     
     
      a
     
     
      d
     
    
    
     (
    
    
     Q
    
    
     ,
    
    
     K
    
    
     ,
    
    
     V
    
    
     )
    
    
     =
    
    
     
      C
     
     
      o
     
     
      n
     
     
      c
     
     
      a
     
     
      t
     
     
      (
     
     
      h
     
     
      e
     
     
      a
     
     
      
       d
      
      
       1
      
     
     
      ,
     
     
      .
     
     
      .
     
     
      .
     
     
      ,
     
     
      h
     
     
      e
     
     
      a
     
     
      
       d
      
      
       h
      
     
     
      )
     
    
    
     
      W
     
     
      O
     
    
    
    
     
      w
     
     
      h
     
     
      e
     
     
      r
     
     
      e
     
     
      &nbsp;
     
     
      h
     
     
      e
     
     
      a
     
     
      
       d
      
      
       i
      
     
     
      =
     
     
      A
     
     
      t
     
     
      t
     
     
      e
     
     
      n
     
     
      t
     
     
      i
     
     
      o
     
     
      n
     
    
    
     (
    
    
     Q
    
    
     
      W
     
     
      i
     
     
      Q
     
    
    
     ,
    
    
     K
    
    
     
      W
     
     
      i
     
     
      K
     
    
    
     ,
    
    
     V
    
    
     
      W
     
     
      i
     
     
      V
     
    
    
     )
    
   
   
     {\rm MultiHead}(Q, K, V) = {\rm Concat(head_1,...,head_h)}W^O \\ {\rm where \ head_i = Attention}(QW_i^Q, KW_i^K, VW_i^V) 
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord"><span class="mord"><span class="mord mathrm">M</span><span class="mord mathrm">u</span><span class="mord mathrm">l</span><span class="mord mathrm">t</span><span class="mord mathrm">i</span><span class="mord mathrm">H</span><span class="mord mathrm">e</span><span class="mord mathrm">a</span><span class="mord mathrm">d</span></span></span><span class="mopen">(</span><span class="mord mathdefault">Q</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span style="margin-right: 0.07153em;" class="mord mathdefault">K</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span style="margin-right: 0.22222em;" class="mord mathdefault">V</span><span class="mclose">)</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 1.14133em; vertical-align: -0.25em;"></span><span class="mord"><span class="mord"><span class="mord mathrm">C</span><span class="mord mathrm">o</span><span class="mord mathrm">n</span><span class="mord mathrm">c</span><span class="mord mathrm">a</span><span class="mord mathrm">t</span><span class="mopen">(</span><span class="mord mathrm">h</span><span class="mord mathrm">e</span><span class="mord mathrm">a</span><span class="mord"><span class="mord mathrm">d</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathrm mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord mathrm">.</span><span class="mord mathrm">.</span><span class="mord mathrm">.</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord mathrm">h</span><span class="mord mathrm">e</span><span class="mord mathrm">a</span><span class="mord"><span class="mord mathrm">d</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.336108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathrm mtight">h</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mclose">)</span></span></span><span class="mord"><span style="margin-right: 0.13889em;" class="mord mathdefault">W</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.891331em;"><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span style="margin-right: 0.02778em;" class="mord mathdefault mtight">O</span></span></span></span></span></span></span></span></span><span class="mspace newline"></span><span class="base"><span class="strut" style="height: 1.2361em; vertical-align: -0.276864em;"></span><span class="mord"><span class="mord"><span style="margin-right: 0.01389em;" class="mord mathrm">w</span><span class="mord mathrm">h</span><span class="mord mathrm">e</span><span class="mord mathrm">r</span><span class="mord mathrm">e</span><span class="mspace">&nbsp;</span><span class="mord mathrm">h</span><span class="mord mathrm">e</span><span class="mord mathrm">a</span><span class="mord"><span class="mord mathrm">d</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.317502em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathrm mtight">i</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mord mathrm">A</span><span class="mord mathrm">t</span><span class="mord mathrm">t</span><span class="mord mathrm">e</span><span class="mord mathrm">n</span><span class="mord mathrm">t</span><span class="mord mathrm">i</span><span class="mord mathrm">o</span><span class="mord mathrm">n</span></span></span><span class="mopen">(</span><span class="mord mathdefault">Q</span><span class="mord"><span style="margin-right: 0.13889em;" class="mord mathdefault">W</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.959239em;"><span class="" style="top: -2.42314em; margin-left: -0.13889em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span><span class="" style="top: -3.18091em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">Q</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.276864em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span style="margin-right: 0.07153em;" class="mord mathdefault">K</span><span class="mord"><span style="margin-right: 0.13889em;" class="mord mathdefault">W</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.891331em;"><span class="" style="top: -2.453em; margin-left: -0.13889em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span style="margin-right: 0.07153em;" class="mord mathdefault mtight">K</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.247em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span style="margin-right: 0.22222em;" class="mord mathdefault">V</span><span class="mord"><span style="margin-right: 0.13889em;" class="mord mathdefault">W</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.891331em;"><span class="" style="top: -2.453em; margin-left: -0.13889em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span style="margin-right: 0.22222em;" class="mord mathdefault mtight">V</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.247em;"><span class=""></span></span></span></span></span></span><span class="mclose">)</span></span></span></span></span></span></p> 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262

Self-Attention与Multi-Head Attention计算量对比

在原论文章节3.2.2中最后有说两者的计算量其实差不多。Due to the reduced dimension of each head, the total computational cost is similar to that of single-head attention with full dimensionality.下面做了个简单的实验，这个model文件大家先忽略哪来的。这个Attention就是实现Multi-head Attention的方法，其中包括上面讲的所有步骤。

首先创建了一个Self-Attention模块（单头）a1，然后把proj变量置为Identity（Identity对应的是Multi-Head Attention中最后那个

      W
     
     
      o
     
    
   
   
    W^o
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord"><span style="margin-right: 0.13889em;" class="mord mathdefault">W</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.664392em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">o</span></span></span></span></span></span></span></span></span></span></span></span>的映射，单头中是没有的，所以置为Identity即不做任何操作）。</li><li>再创建一个<code onclick="mdcp.copyCode(event)" style="user-select: auto;">Multi-Head Attention</code>模块（多头）<code onclick="mdcp.copyCode(event)" style="user-select: auto;">a2</code>，然后设置8个head。</li><li>创建一个随机变量，注意shape</li><li>使用fvcore分别计算两个模块的FLOPs</li></ul> 
1
2
3
4
5
6
7
8
9
10
11
12

import torch
from fvcore.nn import FlopCountAnalysis

from model import Attention


def main():
    # Self-Attention
    a1 = Attention(dim=512, num_heads=1)
    a1.proj = torch.nn.Identity()  # remove Wo

    # Multi-Head Attention
    a2 = Attention(dim=512, num_heads=8)

    # [batch_size, num_tokens, total_embed_dim]
    t = (torch.rand(32, 1024, 512),)

    flops1 = FlopCountAnalysis(a1, t)
    print("Self-Attention FLOPs:", flops1.total())

    flops2 = FlopCountAnalysis(a2, t)
    print("Multi-Head Attention FLOPs:", flops2.total())


if __name__ == '__main__':
    main()

 
 
 
 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

终端输出如下，可以发现确实两者的FLOPs差不多，Multi-Head Attention比Self-Attention略高一点：

Self-Attention FLOPs: 60129542144
Multi-Head Attention FLOPs: 68719476736

 
 
 
 1
2
1
2

其实两者FLOPs的差异只是在最后的

     W
    
    
     O
    
   
  
  
   W^O
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.841331em; vertical-align: 0em;"></span><span class="mord"><span style="margin-right: 0.13889em;" class="mord mathdefault">W</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.841331em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span style="margin-right: 0.02778em;" class="mord mathdefault mtight">O</span></span></span></span></span></span></span></span></span></span></span></span>上，如果把<code onclick="mdcp.copyCode(event)" style="user-select: auto;">Multi-Head Attentio</code>的<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     W
    
    
     O
    
   
  
  
   W^O
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.841331em; vertical-align: 0em;"></span><span class="mord"><span style="margin-right: 0.13889em;" class="mord mathdefault">W</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.841331em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span style="margin-right: 0.02778em;" class="mord mathdefault mtight">O</span></span></span></span></span></span></span></span></span></span></span></span>也删除（即把<code onclick="mdcp.copyCode(event)" style="user-select: auto;">a2</code>的proj也设置成Identity），可以看出两者FLOPs是一样的：</p> 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

Self-Attention FLOPs: 60129542144
Multi-Head Attention FLOPs: 60129542144

 
 
 
 1
2
1
2

Positional Encoding

如果仔细观察刚刚讲的Self-Attention和Multi-Head Attention模块，在计算中是没有考虑到位置信息的。假设在Self-Attention模块中，输入

     a
    
    
     1
    
   
   
    ,
   
   
    
     a
    
    
     2
    
   
   
    ,
   
   
    
     a
    
    
     3
    
   
  
  
   a_1, a_2, a_3
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.625em; vertical-align: -0.19444em;"></span><span class="mord"><span class="mord mathdefault">a</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span class="mord mathdefault">a</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span class="mord mathdefault">a</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">3</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>得到<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     b
    
    
     1
    
   
   
    ,
   
   
    
     b
    
    
     2
    
   
   
    ,
   
   
    
     b
    
    
     3
    
   
  
  
   b_1, b_2, b_3
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.88888em; vertical-align: -0.19444em;"></span><span class="mord"><span class="mord mathdefault">b</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span class="mord mathdefault">b</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span class="mord mathdefault">b</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">3</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>。对于<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     a
    
    
     1
    
   
  
  
   a_1
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.58056em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathdefault">a</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>而言，<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     a
    
    
     2
    
   
  
  
   a_2
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.58056em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathdefault">a</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>和<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     a
    
    
     3
    
   
  
  
   a_3
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.58056em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathdefault">a</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">3</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>离它都是一样近的而且没有先后顺序。假设将输入的顺序改为<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     a
    
    
     1
    
   
   
    ,
   
   
    
     a
    
    
     3
    
   
   
    ,
   
   
    
     a
    
    
     2
    
   
  
  
   a_1, a_3, a_2
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.625em; vertical-align: -0.19444em;"></span><span class="mord"><span class="mord mathdefault">a</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span class="mord mathdefault">a</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">3</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span class="mord mathdefault">a</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>，对结果<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     b
    
    
     1
    
   
  
  
   b_1
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.84444em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathdefault">b</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>是没有任何影响的。下面是使用Pytorch做的一个实验，首先使用<code onclick="mdcp.copyCode(event)" style="user-select: auto;">nn.MultiheadAttention</code>创建一个<code onclick="mdcp.copyCode(event)" style="user-select: auto;">Self-Attention</code>模块（<code onclick="mdcp.copyCode(event)" style="user-select: auto;">num_heads=1</code>），注意这里在正向传播过程中直接传入<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    Q
   
   
    K
   
   
    V
   
  
  
   QKV
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.87777em; vertical-align: -0.19444em;"></span><span class="mord mathdefault">Q</span><span style="margin-right: 0.07153em;" class="mord mathdefault">K</span><span style="margin-right: 0.22222em;" class="mord mathdefault">V</span></span></span></span></span>，接着创建两个顺序不同的<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    Q
   
   
    K
   
   
    V
   
  
  
   QKV
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.87777em; vertical-align: -0.19444em;"></span><span class="mord mathdefault">Q</span><span style="margin-right: 0.07153em;" class="mord mathdefault">K</span><span style="margin-right: 0.22222em;" class="mord mathdefault">V</span></span></span></span></span>变量t1和t2（主要是将<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     q
    
    
     2
    
   
   
    ,
   
   
    
     k
    
    
     2
    
   
   
    ,
   
   
    
     v
    
    
     2
    
   
  
  
   q^2, k^2, v^2
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.00855em; vertical-align: -0.19444em;"></span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">q</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.814108em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span style="margin-right: 0.03148em;" class="mord mathdefault">k</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.814108em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">v</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.814108em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span></span></span></span></span>和<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    
     q
    
    
     3
    
   
   
    ,
   
   
    
     k
    
    
     3
    
   
   
    ,
   
   
    
     v
    
    
     3
    
   
  
  
   q^3, k^3, v^3
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.00855em; vertical-align: -0.19444em;"></span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">q</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.814108em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">3</span></span></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span style="margin-right: 0.03148em;" class="mord mathdefault">k</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.814108em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">3</span></span></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">v</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.814108em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">3</span></span></span></span></span></span></span></span></span></span></span></span>的顺序换了下），分别将这两个变量输入Self-Attention模块进行正向传播。</p> 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294

import torch
import torch.nn as nn


m = nn.MultiheadAttention(embed_dim=2, num_heads=1)

t1 = [[[1., 2.],   # q1, k1, v1
       [2., 3.],   # q2, k2, v2
       [3., 4.]]]  # q3, k3, v3

t2 = [[[1., 2.],   # q1, k1, v1
       [3., 4.],   # q3, k3, v3
       [2., 3.]]]  # q2, k2, v2

q, k, v = torch.as_tensor(t1), torch.as_tensor(t1), torch.as_tensor(t1)
print("result1: \n", m(q, k, v))

q, k, v = torch.as_tensor(t2), torch.as_tensor(t2), torch.as_tensor(t2)
print("result2: \n", m(q, k, v))

 
 
 
 1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/小丑西瓜9/article/detail/92928