在线性回归模型中，因变量与自变量之间存在线性关系，并试图找到最佳拟合直线来描述这种关系。其数学表达式为：Y = β0 + β1X1 + β2X2 + ... + βn*Xn + ε，其中Y是因变量，X是自变量，β是回归系数。如果回归分析中只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。

在线性回归算法中，我们会通过cost/loss函数计算权重和偏移量。损失函数(Loss/Error Function)是计算单个训练集的误差，而代价函数(Cost Function)则是计算整个训练集所有损失之和的平均值。

在实际应用中，例如预测房价的例子中，我们可以通过构建线性回归模型来寻找房价与面积之间的线性关系，从而利用该模型进行房价预测。总的来说，线性回归是一种强大且灵活的工具，可以应用于许多实际问题中。

一元一次线性回归公式及解析

应用案例（一）——自定义数据（Custom data）

1、下载安装sklearn库

Anaconda Prompt：pip install sklearn

sklearn，全称scikit-learn，是一个基于Python的开源机器学习工具包。它提供了各种分类、回归和聚类算法，包括但不限于支持向量机、随机森林、梯度提升、k均值和DBSCAN等。此外，它还包含了许多常用的机器学习算法、预处理技术、模型选择和评估工具等，可以方便地进行数据挖掘。这个库通过集成NumPy, SciPy和Matplotlib等Python数值计算的库实现了高效的算法应用。可以说，sklearn是机器学习中一个非常常用且功能强大的Python第三方模块。

2、导入库函数


import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression#用于从sklearn库中导入线性回归模型。

3、加载数据集


x=np.array([10,20,30,40,50,60])#腰围——independent variable（独立型变量）——特征
y=np.array([15,45,50,70,110,130])#体重——dependent variable（依赖型变量）——预测值

4、创建线性回归对象

linreg=LinearRegression()#创建LinearRegression类的实例对象

X=x.reshape(-1,1)#-1表示所有行，1表示变成1列。——将数组x重塑为列向量。

x=np.array([10,20,30,40,50,60])

X=x.reshape(-1,1)#-1表示所有行，1表示变成1列。——将数组x重塑为列向量。

在这两句代码中，x是一个一维的NumPy数组，而X是一个二维的NumPy数组。

将x转换为X的目的是将其重塑为一个列向量，其中每个元素都是原始数组中的一个元素。这样做是为了符合某些机器学习算法的要求，例如线性回归模型需要输入的数据是二维的（特征矩阵）。

具体来说，reshape(-1, 1)函数将x重塑为一个列向量，其中-1表示自动计算该维度的大小。在这种情况下，由于x只有6个元素，所以重塑后的X将是一个6行1列的二维数组。

因此，通过将x转换为X，我们可以将其作为机器学习算法的输入数据进行进一步处理和训练。

x与X的区别：

X和原本的x在形状上有所不同。原本的x是一个一维数组，而X是一个二维数组，其中每一行都是原本的x中的元素。具体来说，如果原本的x包含n个元素，那么X将包含n行和1列。

5、模型训练

1、fit()：在机器学习中，fit函数是一个核心方法，主要用于训练模型。以线性回归模型为例，fit函数可以用于计算最佳拟合参数。

具体来说，当我们创建一个线性回归模型对象后，可以使用fit函数来拟合我们的数据。例如：

linreg.fit(X,y)#因为本应用案例数据集很小，所以并没有做训练集和测试集的拆分

6、预测结果

因为此案例中的数据量非常小，所以没有划分训练集和测试集，因为意义不大。所以，此处的训练集和测试集是相同的。

y_predict=linreg.predict(X)#使用线性回归模型 linreg 对输入数据 X 进行预测，并将预测结果存储在变量 y_predict 中

7、绘制模型图像


plt.scatter(X,y,c="g")#真实值
 
plt.scatter(X,y_predict,c="b")#预测值
 
plt.plot(X,y_predict,'Red')#回归模型
 
plt.show()

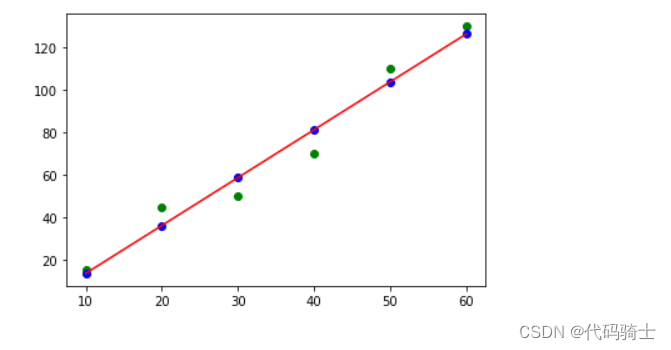
8、应用模型进行预测

linreg.predict([[75]])#注意线性回归模型传入的参数必须是二维数组

9、评估指标


from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
 
# 评估指标
mse = mean_squared_error(y, y_predict)
rmse = np.sqrt(mse)
mae = mean_absolute_error(y, y_predict)
r2 = r2_score(y, y_predict)
 
print("均方误差（MSE）：", mse)
print("均方根误差（RMSE）：", rmse)
print("平均绝对误差（MAE）：", mae)
print("R2分数：", r2)

均方误差（MSE）： 55.71428571428573
均方根误差（RMSE）： 7.46420027292179
平均绝对误差（MAE）： 6.666666666666668
R2分数： 0.9638610038610038

这些指标都是用来衡量线性回归模型的预测性能的。

均方误差（MSE）：它是实际观察值与预测值之间差的平方的平均值，数值越小表示模型的拟合效果越好。在这个例子中，MSE为55.71428571428573，比较大，说明模型的预测精度不高。
均方根误差（RMSE）：它是MSE的平方根，也是衡量模型预测精度的一种常用指标。在这个例子中，RMSE为7.46420027292179，也比较大，说明模型的预测精度不高。
平均绝对误差（MAE）：它是实际观察值与预测值之间差的绝对值的平均值，数值越小表示模型的拟合效果越好。在这个例子中，MAE为6.666666666666668，也比较大，说明模型的预测精度不高。
R2分数：它是决定系数，用于衡量模型对数据的拟合程度。它的取值范围在0到1之间，越接近1表示模型对数据的拟合程度越高。在这个例子中，R2分数为0.9638610038610038，比较接近1，说明模型对数据的拟合程度较高。

综合来看，这个线性回归模型对数据的拟合程度较高，但预测精度不高。可能需要进一步优化模型或者考虑使用其他类型的回归模型来提高预测精度。

应用案例（二）——Age, Weight, Height, BMI Analysis

数据来源于kaggle：

Age, Weight, Height, BMI Analysis | Kaggle

Step1：加载函数库


#处理数据
import numpy as np
import pandas as pd
#绘制图像
import matplotlib.pyplot as plt
import seaborn as sns
#机器学习模型
from sklearn.linear_model import LinearRegression

Step2：获取数据（Get Data）

df = pd.read_csv("./kaggle-data/bmi.csv")

Step3：数据分析（Data Analysis）

df["BmiClass"].unique()

array(['Obese Class 1', 'Overweight', 'Underweight', 'Obese Class 2',
       'Obese Class 3', 'Normal Weight'], dtype=object)

df.corr()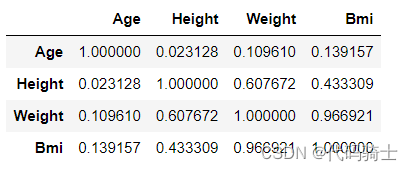

sns.heatmap(df.corr())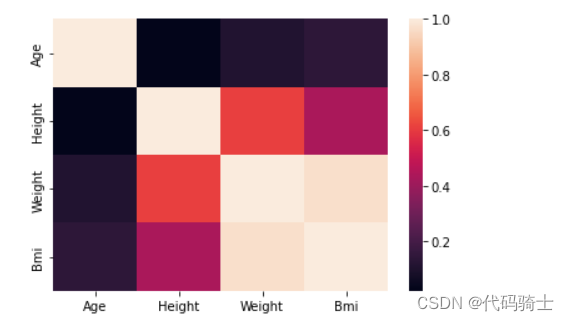

Step4：划分特征集（独立变量independent variable）和响应集（dependent variable）

分析：Weight-Bmi


x = df["Weight"]
x = np.array(x)

X=x.reshape(-1,1)#-1表示所有行，1表示变成1列。——将数组x重塑为列向量。(因为fit函数中的X必须是二维数组)


y = df["Bmi"]
y = np.array(y)

Step5：划分训练集与测试集


from sklearn.model_selection import train_test_split
 
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30, random_state=42)

Step6：创建模型并训练


linreg=LinearRegression()#创建LinearRegression类的实例对象
linreg.fit(X,y)

Step7:模型预测

y_predict=linreg.predict(X_test)


plt.scatter(X,y,c="g")#原始点值
 
#plt.scatter(X,y_predict,c="b")#预测点值
 
plt.plot(X_test,y_predict,'Red')#预测直线
 
plt.show()


print(linreg.coef_)#输出斜率
 
print(linreg.intercept_)#截距
 
linreg.predict([[75]])#预测75的值

Step8：评估指标


from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
 
# 评估指标
mse = mean_squared_error(y_test, y_predict)
rmse = np.sqrt(mse)
mae = mean_absolute_error(y_test, y_predict)
r2 = r2_score(y_test, y_predict)
 
print("均方误差（MSE）：", mse)
print("均方根误差（RMSE）：", rmse)
print("平均绝对误差（MAE）：", mae)
print("R2分数：", r2)

均方误差（MSE）： 5.317227468654762
均方根误差（RMSE）： 2.3059114182150973
平均绝对误差（MAE）： 1.4445498844767182
R2分数： 0.930531636814612

这些指标都是用来衡量线性回归模型的预测性能的。

均方误差（MSE）：它是实际观察值与预测值之间差的平方的平均值，数值越小表示模型的拟合效果越好。在这个例子中，MSE为5.317227468654762。
均方根误差（RMSE）：它是MSE的平方根，也是衡量模型预测精度的一种常用指标。在这个例子中，RMSE为2.3059114182150973。
平均绝对误差（MAE）：它是实际观察值与预测值之间差的绝对值的平均值，数值越小表示模型的拟合效果越好。在这个例子中，MAE为1.4445498844767182。
R2分数：它是决定系数，用于衡量模型对数据的拟合程度。它的取值范围在0到1之间，越接近1表示模型对数据的拟合程度越高。在这个例子中，R2分数为0.930531636814612。

综合来看，这个线性回归模型的预测性能较好，但还有改进的空间。

分析：Weight-Height


#处理数据
import numpy as np
import pandas as pd
#绘制图像
import matplotlib.pyplot as plt
import seaborn as sns
#机器学习模型
from sklearn.linear_model import LinearRegression
 
df = pd.read_csv("./kaggle-data/bmi.csv")


x = np.array(df["Weight"])
X=x.reshape(-1,1)#-1表示所有行，1表示变成1列。——将数组x重塑为列向量。(因为fit函数中的X必须是二维数组)
y = np.array(df["Height"])


from sklearn.model_selection import train_test_split
 
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30, random_state=42)
linreg=LinearRegression()#创建LinearRegression类的实例对象
linreg.fit(X,y)
y_predict=linreg.predict(X_test)
y_predict


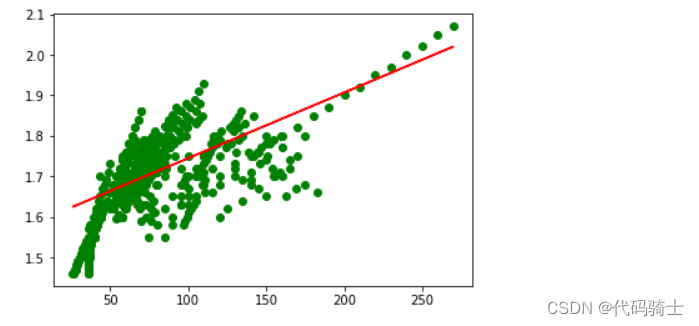
plt.scatter(X,y,c="g")#原始点值
 
#plt.scatter(X,y_predict,c="b")#预测点值
 
plt.plot(X_test,y_predict,'Red')#预测直线
 
plt.show()


from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
 
# 评估指标
mse = mean_squared_error(y_test, y_predict)
rmse = np.sqrt(mse)
mae = mean_absolute_error(y_test, y_predict)
r2 = r2_score(y_test, y_predict)
 
print("均方误差（MSE）：", mse)
print("均方根误差（RMSE）：", rmse)
print("平均绝对误差（MAE）：", mae)
print("R2分数：", r2)

均方误差（MSE）： 0.004602807109702035
均方根误差（RMSE）： 0.0678439909623692
平均绝对误差（MAE）： 0.05320966584449583
R2分数： 0.3970282667901889

这些指标都是用来衡量线性回归模型的预测性能的。

均方误差（MSE）：它是实际观察值与预测值之间差的平方的平均值，数值越小表示模型的拟合效果越好。在这个例子中，MSE为0.004602807109702035，非常小，说明模型的预测精度很高。
均方根误差（RMSE）：它是MSE的平方根，也是衡量模型预测精度的一种常用指标。在这个例子中，RMSE为0.0678439909623692，也比较小，说明模型的预测精度很高。
平均绝对误差（MAE）：它是实际观察值与预测值之间差的绝对值的平均值，数值越小表示模型的拟合效果越好。在这个例子中，MAE为0.05320966584449583，也较小，说明模型的预测精度很高。
R2分数：它是决定系数，用于衡量模型对数据的拟合程度。它的取值范围在0到1之间，越接近1表示模型对数据的拟合程度越高。在这个例子中，R2分数为0.3970282667901889，比较低，说明模型对数据的拟合程度不高。

综合来看，这个线性回归模型的预测精度很高，但模型对数据的拟合程度不高。可能需要进一步优化模型或者考虑使用其他类型的回归模型来提高拟合程度。

linreg.predict([[90]])

array([1.72819609])

二、MultipleLinear Regression多元线性回归应用

多元线性回归是一种用于评估一个因变量与多个自变量之间关系的方法。如果因变量的变化受到两个或两个以上重要因素的影响，就需要采用多元线性回归进行分析。其基本原理和计算过程与一元线性回归相同，但由于自变量个数多，计算过程相当复杂，通常需要借助统计软件进行运算。

在多元线性回归模型中，设y为因变量，X1, X2…Xk为自变量，且自变量与因变量之间存在线性关系。此时，多元线性回归模型可以表示为：Y=b0+b1x1+…+bkxk+e。其中，b0是常数项，b1, b2…bk是回归系数。具体来说，b1代表当X1, X2…Xk固定时，x1每增加一个单位对y的影响，即x1对y的偏回归系数；类似地，b2表示当X1, X2…Xk固定时，x2每增加一个单位对y的影响，即x2对y的偏回归系数。

需要注意的是，进行多元线性回归分析时需要满足一些条件，如一元线性回归、多个自变量之间不存在多重共线、正态性、独立性、方差齐性等。在实际运用中，可以通过因素分析和回归诊断来进一步解释和预测因变量的变化。

多元一次线性回归公式及解析

应用案例（一）美国初创公司盈利数据分析

1、导入函数库


#数据处理
import numpy as np
import pandas as pd
#绘图
import matplotlib.pyplot as plt
import seaborn as sns

2、加载数据集


#https://www.kaggle.com/farhanmd29/50-startups
dataset = pd.read_csv('./kaggle-data/startups.csv')

3、数据分析

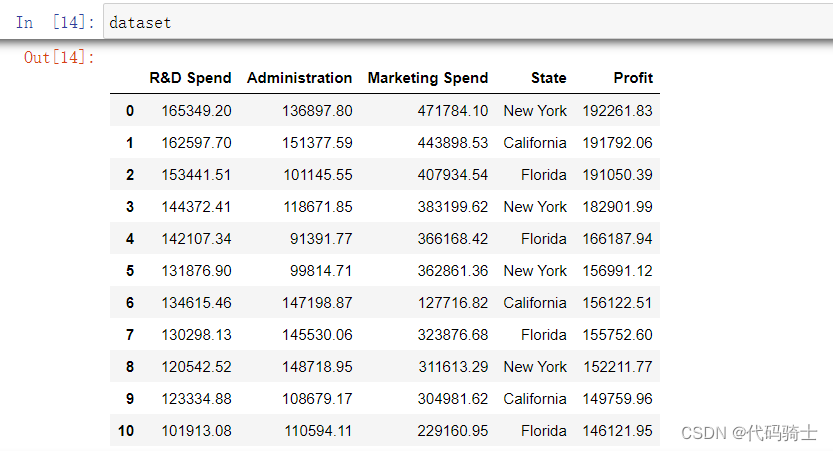
R&D Spend-研发费用

Administration-管理费用

Marketing Spend -市场营销支出

State-州

Profit-盈利

4、数据处理


#划分特征集和响应集
x = dataset.drop("Profit",axis=1)# inplace: 默认'bool' = False，若为true，则原数据集dataset也会跟着drop
#或者通过iloc选取：X = dataset.iloc[:, 0:4]
y = dataset["Profit"]
#y = dataset.iloc[:, 4]#第四列元素

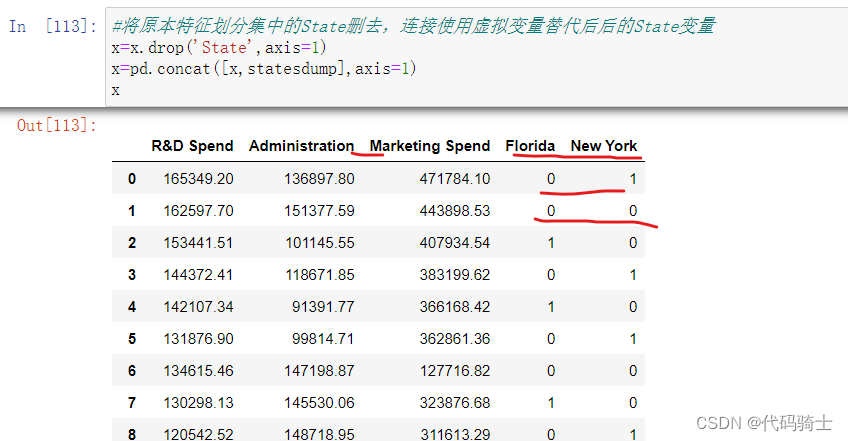
(1)变量类型转换

State列不是数字而是字符，需要转变成数字类型，计算机才能进行计算

通过pandas库里的get_dummies函数，将State里面的三种不同变量用虚拟变量0\1表示。

get_dummies 是一个常用于处理分类变量的函数，它能够将分类变量转换为虚拟变量（dummy variables）。在Python中，可以使用pandas库中的 get_dummies 函数来实现这一功能。

pd.get_dummies(x['State'])


#因为三个State是相互互斥的关系，所以用2个bit位就能表示三种关系。
statesdump=pd.get_dummies(x['State'],drop_first=True)


#将原本特征划分集中的State删去，连接使用虚拟变量替代后后的State变量
x=x.drop('State',axis=1)
x=pd.concat([x,statesdump],axis=1)
x

5、数据集拆分


#划分数据集为测试集和训练集
from sklearn.model_selection import train_test_split
 
X_train, X_test, y_train, y_test = train_test_split(x, y, test_size = 0.3, random_state = 42)

6、模型建立与训练


from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
model=regressor.fit(X_train, y_train)

7、模型预测与评估


from sklearn.metrics import r2_score
y_predict = regressor.predict(X_test)
score1=r2_score(y_test,y_predict)

应用案例（二）Age、Height、Weight、Bmi数据分析


#处理数据
import numpy as np
import pandas as pd
#绘制图像
import matplotlib.pyplot as plt
import seaborn as sns
#机器学习模型
from sklearn.linear_model import LinearRegression

df = pd.read_csv("./kaggle-data/bmi.csv")

X = df.iloc[:,:3]

y = df.loc[:,"Bmi"]


from sklearn.model_selection import train_test_split
 
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30, random_state=42)
linreg=LinearRegression()#创建LinearRegression类的实例对象
linreg.fit(X,y)


from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
 
# 评估指标
mse = mean_squared_error(y_test, y_predict)
rmse = np.sqrt(mse)
mae = mean_absolute_error(y_test, y_predict)
r2 = r2_score(y_test, y_predict)
 
print("均方误差（MSE）：", mse)
print("均方根误差（RMSE）：", rmse)
print("平均绝对误差（MAE）：", mae)
print("R2分数：", r2)

根据你提供的模型评价指标，可以看出该模型的预测准确性较高。具体来说：

均方误差（MSE）为2.3184863195143905，这个值较小，说明模型预测值与真实值之间的差距相对较小。
均方根误差（RMSE）为1.522657650134918，也是较小的值，反映了模型预测的平均误差大小。
平均绝对误差（MAE）为0.7340409980692838，同样是一个较小的值，也说明了模型预测的准确性较高。
R2分数为0.9697095054454898，接近于1，说明模型可以解释因变量变化的能力较强。

综上所述，该模型的预测准确性较高，并且能够较好地解释因变量的变化。


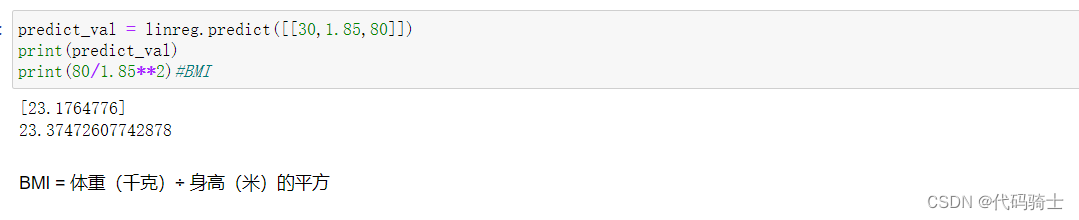
predict_val = linreg.predict([[30,1.85,80]])
print(predict_val)
print(80/1.85**2)#BMI

三、Polynomial (Linear) Regression多项式线性回归

多项式线性回归是一种扩展了线性回归模型的方法，通过引入多项式函数来拟合非线性数据。它是一个强大的工具，可以在多种实际问题中使用。多项式回归模型是线性回归模型的一种，此时回归函数关于回归系数是线性的。由于任一函数都可以用多项式逼近，因此多项式回归有着广泛应用。

多项式线性回归公式及解析

应用案例（一）年龄与身高关系数据分析

1、导入函数库


# Import necessary libraries 
import pandas as pd 
import numpy as np 
import matplotlib.pyplot as plt 
import seaborn as sns

2、加载数据集


# Import the Height Weight Dataset 
data = pd.read_excel('./kaggle-data/age-height.xlsx')

3、划分数据集


#Store the data in the form of dependent and independent variables separately
X = data.iloc[:, 0:1] #全部行，第0列
#X = data.iloc[:, 0:-1].values#如果数据集过大，可以用-1表示到最后一行或最后一列
y = data.iloc[:, 1]#全部行，第1列

4、模型训练与预测

拆分数据集（训练集、测试集）


#Split the Dataset into Training and Test Dataset
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

（1）使用一次线性回归模型进行预测和评估


#Fit the Simple Linear Regression Model
from sklearn.linear_model import LinearRegression
LinReg = LinearRegression()
LinReg.fit(X_train, y_train)
#用r2得分进行评估
from sklearn.metrics import r2_score
score1=r2_score(y_test,LinReg.predict(X_test))
print(score1)

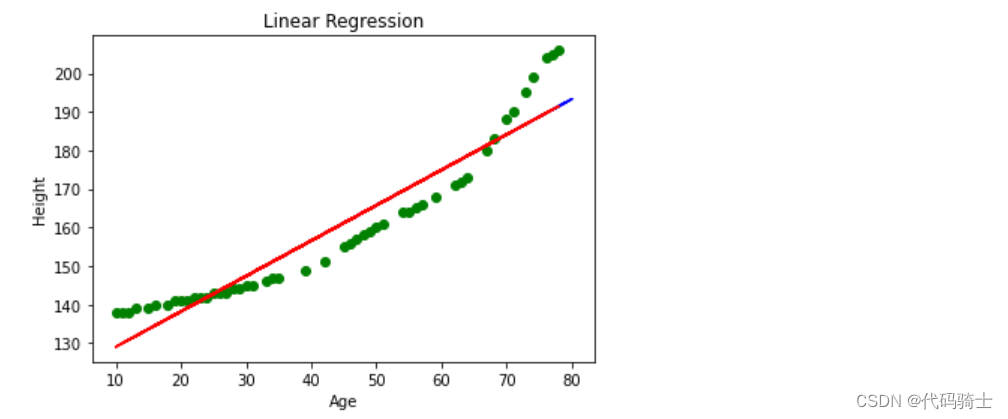
一次线性回归模型图像


# Visualise the Linear Regression Result
plt.scatter(X_train, y_train, color = 'green') 
  
plt.plot(X_test, LinReg.predict(X_test), color = 'blue') 
plt.plot(X_train, LinReg.predict(X_train), color = 'red') 
plt.title('Linear Regression') 
plt.xlabel('Age') 
plt.ylabel('Height') 
 
plt.show()

（2）使用多项式线性回归模型进行预测和评估


# Add the polynomial term to the equation/model
from sklearn.preprocessing import PolynomialFeatures 
 
polynom = PolynomialFeatures(degree = 2) #多项式算到平方。——1+ax+bx^2
X_polynom = polynom.fit_transform(X_train)#将原始数据转换为多项式特征表示

X_polynom = polynom.fit_transform(X_train) 这行代码的意思是使用多项式回归模型对训练数据 X_train 进行拟合，并将拟合后的数据存储在变量 X_polynom 中。

具体来说，polynom 是一个多项式回归模型的实例化对象，fit_transform() 是该对象的一个方法，用于对输入数据进行拟合和转换。该方法会返回一个新的数组，其中包含了经过多项式变换后的训练数据。

通过执行这行代码，你可以将原始的训练数据 X_train 转换为多项式特征表示，以便后续的机器学习算法可以更好地处理这些数据。


#Fit the Polynomial Regression Model 
PolyReg = LinearRegression() 
PolyReg.fit(X_polynom, y_train)#拟合


#用r2得分进行评估
from sklearn.metrics import r2_score
score2=r2_score(y_test,PolyReg.predict(polynom.fit_transform(X_test)))#将测试集X_test也转化成多项式表示形式
print(score2)

0.9892511710983519


# Visualise the Polynomial Regression Results 
plt.scatter(X_train, y_train, color = 'green') 
#plt.scatter(X_test, y_test, color = 'green') 
 
plt.plot(X_train, PolyReg.predict(polynom.fit_transform(X_train)), color = 'red') #PolyReg.predict(polynom.fit_transform(X_train))——多项式线性模型对X_train的预测
#plt.plot(X_test, PolyReg.predict(polynom.fit_transform(X_test)), color = 'blue') #PolyReg.predict(polynom.fit_transform(X_train))——多项式线性模型对X_test的预测
plt.title('Polynomial Regression')
plt.xlabel('Age') 
plt.ylabel('Height') 
 
plt.show()

（3）调整模型参数对多项式模型进行优化


# Add the polynomial term to the equation/model
from sklearn.preprocessing import PolynomialFeatures 
 
polynom = PolynomialFeatures(degree = 3) #多项式算到平方。——1+ax+bx^2
X_polynom = polynom.fit_transform(X_train)#将原始数据转换为多项式特征表示
#Fit the Polynomial Regression Model 
PolyReg = LinearRegression() 
PolyReg.fit(X_polynom, y_train)#拟合
#用r2得分进行评估
from sklearn.metrics import r2_score
score2=r2_score(y_test,PolyReg.predict(polynom.fit_transform(X_test)))#将测试集X_test也转化成多项式表示形式
print(score2)

0.9927634092096052

PolyReg.predict(polynom.fit_transform([[50]]))

array([158.21534659])

应用案例（二）NBA球员数据分析（包含1996年至2021年季节的所有数据）


# Import necessary libraries 
import pandas as pd 
import numpy as np 
import matplotlib.pyplot as plt 
import seaborn as sns


# Import the Height Weight Dataset 
#https://www.kaggle.com/datasets/justinas/nba-players-data
data = pd.read_csv('./kaggle-data/nba_all_seasons.csv')

list(data.columns)

'Unnamed: 0',
'player_name',姓名
'team_abbreviation',球员所效力球队的缩写名称(赛季末)
'age',年龄
'player_height',身高
'player_weight',体重
'college',球员就读的大学名称
'country',球员出生的国家名称(不一定是国籍)
'draft_year',选秀当年
'draft_round',选秀选手被选中了
'draft_number',选秀顺位
'gp',表示球员在某个赛季或某个时间段内参加的比赛场次。
'pts', 得分。这是球员在每场比赛中获得的平均得分。
'reb',篮板。这是球员在每场比赛中获得的平均篮板数。
'ast',助攻。这是球员在每场比赛中送出的平均助攻数。
'net_rating',净效率。这是衡量球员对球队正负影响的统计数据。正值表示球员在场时球队得分多于失分，负值表示球员出场时球队失分多于得分。
'oreb_pct',前场篮板百分比。这是球员抢到前场篮板球的比率。
'dreb_pct',后场篮板百分比。这是球员抢到后场篮板球的比率。
'usg_pct',使用率。这是衡量球员在进攻中对球的控制程度的统计数据。它等于球员的投篮次数、助攻次数和失误次数之和除以球队的总出手次数。
'ts_pct',真实命中率。这是衡量球员投篮效率的统计数据。它等于球员的得分除以他出手的次数。
'ast_pct',助攻率。这是衡量球员助攻能力的统计数据。它等于球员的助攻次数除以球队的总助攻次数。
'season'赛季


x = np.array(data["player_height"])
 
X = x.reshape(-1,1)#转换成列向量（二维数组）
 
y = data["player_weight"]


#Split the Dataset into Training and Test Dataset
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)


# Add the polynomial term to the equation/model
from sklearn.preprocessing import PolynomialFeatures 
 
polynom = PolynomialFeatures(degree = 3) 
X_polynom = polynom.fit_transform(X_train)#将原始数据转换为多项式特征表示
#Fit the Polynomial Regression Model 
PolyReg = LinearRegression() 
PolyReg.fit(X_polynom, y_train)#拟合


#用r2得分进行评估
from sklearn.metrics import r2_score
score2=r2_score(y_test,PolyReg.predict(polynom.fit_transform(X_test)))#将测试集X_test也转化成多项式表示形式
print(score2)

0.6870350501346214


# Visualise the Polynomial Regression Results 
plt.scatter(X_train, y_train, color = 'green') 
#plt.scatter(X_test, y_test, color = 'green') 
 
plt.plot(X_train, PolyReg.predict(polynom.fit_transform(X_train)), color = 'red') #PolyReg.predict(polynom.fit_transform(X_train))——多项式线性模型对X_train的预测
#plt.plot(X_test, PolyReg.predict(polynom.fit_transform(X_test)), color = 'blue') #PolyReg.predict(polynom.fit_transform(X_train))——多项式线性模型对X_test的预测
plt.title('Polynomial Regression')
plt.xlabel('Age') 
plt.ylabel('Height') 
 
plt.show()

四、MultiCollinearity In Linear Regression多重共线性及VIF应用

多重共线性（Multicollinearity）是指线性回归模型中自变量之间存在高度相关性的情况。当两个或多个自变量之间存在较高的相关性时，它们对因变量的解释能力会相互影响，导致模型的不稳定性和不准确性。

为了检测多重共线性，可以使用方差膨胀因子（Variance Inflation Factor, VIF）。VIF是一个衡量自变量之间相关性的指标，其值越大表示自变量之间的相关性越强。通常认为，如果一个自变量的VIF大于10，则说明该自变量与其他自变量之间存在严重的多重共线性问题。根据不同的标准，实际上，VIF超过4就已经值得多加注意了。

解决多重共线性的方法包括：

1. 删除一些自变量：通过逐步回归等方法，选择出对因变量解释能力最强的自变量，并删除其他相关性较强的自变量。
2. 增加样本量：增加样本量可以降低自变量之间的相关性，从而减少多重共线性的影响。
3. 使用岭回归（Ridge Regression）或Lasso回归等正则化方法：这些方法可以通过向损失函数中添加惩罚项来限制自变量之间的相关性，从而减少多重共线性的影响。
4. 主成分分析（Principal Component Analysis, PCA）：PCA可以将原始自变量转换为一组新的无关变量，从而减少多重共线性的影响。

VIF公式及解析

代码示例（一）解决多重共线性问题

1、导入函数库


# Import necessary libraries 
import pandas as pd 
import numpy as np 
import matplotlib.pyplot as plt 
import seaborn as sns

2、载入数据集


#加载数据集
df=pd.read_csv('./kaggle-data/salary_data.csv')

3、划分特征集和响应集


#取特征列
X=X1=df.iloc[:,:-1]#取全部行，最后一列之前的全部列
#取响应列
y=df.iloc[:,-1]#全部行，只取最后一列

4、多重共线性判断方法

特征之间关联性越强，共线性就越大。所以我们必须找出关联性强的特征进行降关联处理，提高模型泛化能力。

（1）关联矩阵法


#当特征数量较少时，我们可以通过关联矩阵的方式快速找出相关性强的变量
X.corr()#查看相关性矩阵——观察各个特征之间的相关性
#如果y的值与特征变量x之间的数值越大，则说明y对x的依赖性越强，说明变量y非常符合依赖型变量的特点，is good
#如果特征变量x与x之间的相关性越大，则说明特征变量x与x之间独立性更小，is very bad

由此可见，Age与YearsExperience具有极强的关联性。

（2）绘图法

sns.pairplot(X)#绘制配对图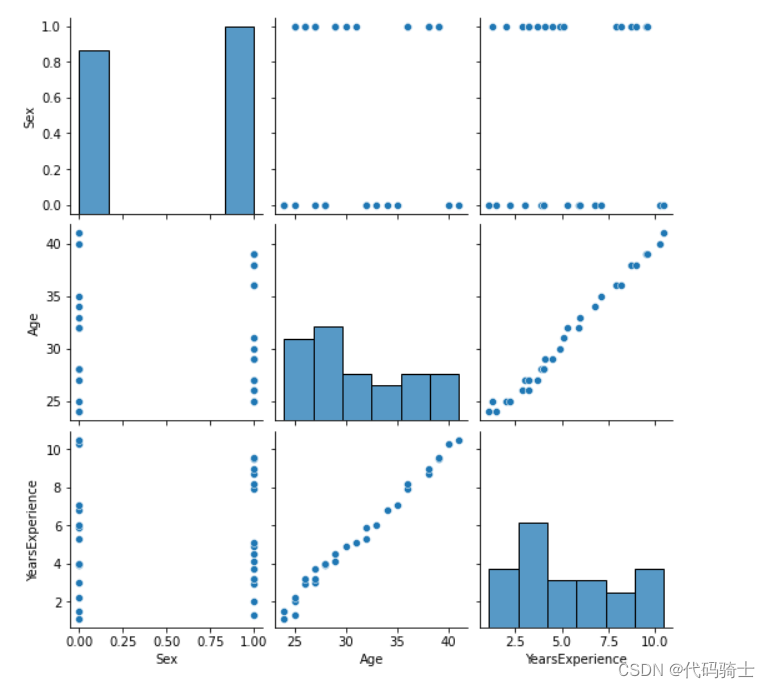

由此可见，Age与YearsExperience具有极强的关联性。

（3）使用VIF（必须使用）

安装VIF库指令：

pip install statsmodels

conda install -c conda-forge statsmodels


#逐一查看各特征与其他特征的VIF(方差扩大因子)
from statsmodels.stats.outliers_influence import variance_inflation_factor
 
print(variance_inflation_factor(X.values, 0))
print(variance_inflation_factor(X.values, 1))
print(variance_inflation_factor(X.values, 2))

2.1349098210011803
12.138592602889707
10.367631468765076


#还有一种更方便的方法是用封装好的VIF接口：
from statsmodels.stats.outliers_influence import variance_inflation_factor
 
def vif(X):
 
    # Calculating VIF
    vif = pd.DataFrame()
    vif["variables"] = X.columns
    vif["VIF"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
 
    return(vif)


# 将数据样本X（全部的特征变量列）直接作为参数传入，就可以得到各特征相对于其他特征的VIF值。
vif(X)

据图分析，Age和YearsExperience都大于10，关联性极强。


#在X中除去Age列
X=X.drop('Age',axis=1)

drop函数是一个在数据处理中常用的函数，特别是在处理Pandas库中的DataFrame数据类型时。它的主要功能是删除数据集中的多余数据。

它的语法格式为：DataFrame.drop (labels=None, axis=0, index=None, columns=None, level=None, inplace=False, errors='raise')。

其中，一些主要的参数含义如下：

labels: 表示待删除的行名或列名；
axis: 表示删除时所参考的轴，0代表行，1代表列；
index: 表示待删除的行名；
columns: 表示待删除的列名；
level: 用于多级列表时，暂不详细说明；
inplace: 这是一个布尔值，默认为False，意味着返回的是数据的副本。如果设为True，则返回删除相应数据后的版本；
errors: 这个参数一般用不到，这里不作解释。


#再次检测VIF
vif(X)

剩余变量的VIF都小于4，正常。

注意：每次删除一个变量都需要再次重新计算VIF，因为VIF是随特征变化而变化的。

（4）最小二乘法(又称最小平方法)

函数名： statsmodels.regression.linear_model.OLS Ordinary Least Squares

最小二乘法，又称最小平方法，是一种数学优化技术。它通过最小化误差（真实目标对象与拟合目标对象的差）的平方和寻找数据的最佳函数匹配。这种方法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。

在线性回归中，最小二乘法主要用来求解回归系数，使得所有样本点到回归直线的距离的平方和最小。对于非线性回归问题，可以通过将非线性模型转化为线性模型来使用最小二乘法。此外，最小二乘法还可以应用于测量数据处理的平差公式中，如矩阵的最小二乘法常用于此。

X2=sm.add_constant(X1)#在X1的第1列添加常数1。例如多项式回归中：1+ax+bx^2+cx^3+……


#用响应列y和特征列X2通过最小二乘法模型做拟合 
model=sm.OLS(y,X2).fit() #Ordinary Least Squares最小二乘法(又称最小平方法)

model.summary()#查看模型摘要，获取关键信息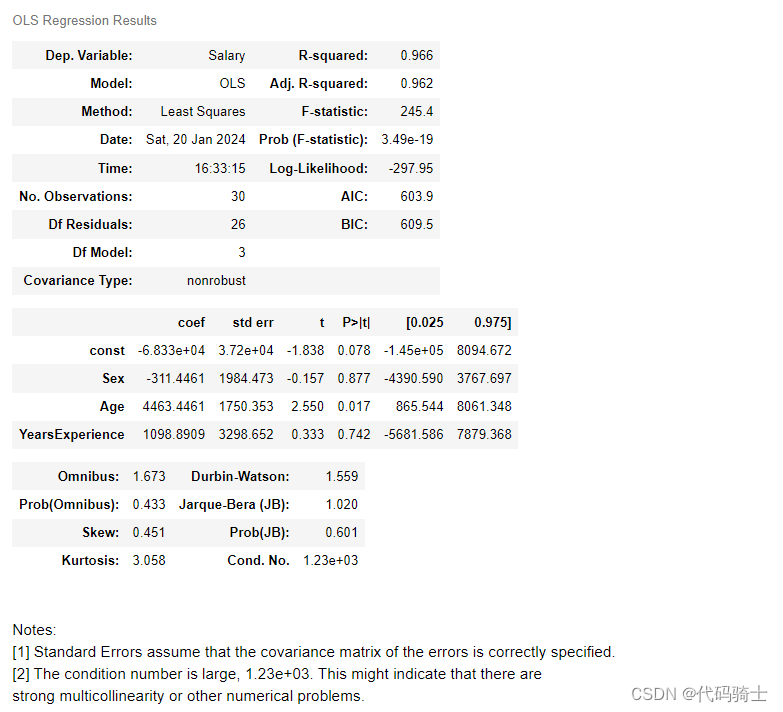

应用案例（一）波士顿房价预测

1、导入函数库


# Import necessary libraries 
import pandas as pd 
import numpy as np 
import matplotlib.pyplot as plt 
import seaborn as sns

2、加载数据集


from sklearn.datasets import load_boston#载入波士顿房价预测数据
 
boston=load_boston()#加载数据集

3、划分数据集

X=pd.DataFrame(boston['data'])

Bunch is a subclass of the Dict class and supports all the methods as dict does. In addition, it allows you to use the keys as attributes.

Bunch是Dict类的子类，支持所有与dict相同的方法。此外，它还允许您将键用作属性。

X.columns=boston['feature_names']


#给特征集添加标签
X.columns=boston['feature_names']

4、寻找关联性强的特征

（1）corr

X.corr()

数据列太多了，肉眼难以辨别

（2）绘制热力图


plt.figure(figsize = (10,8))
sns.heatmap(X.corr())

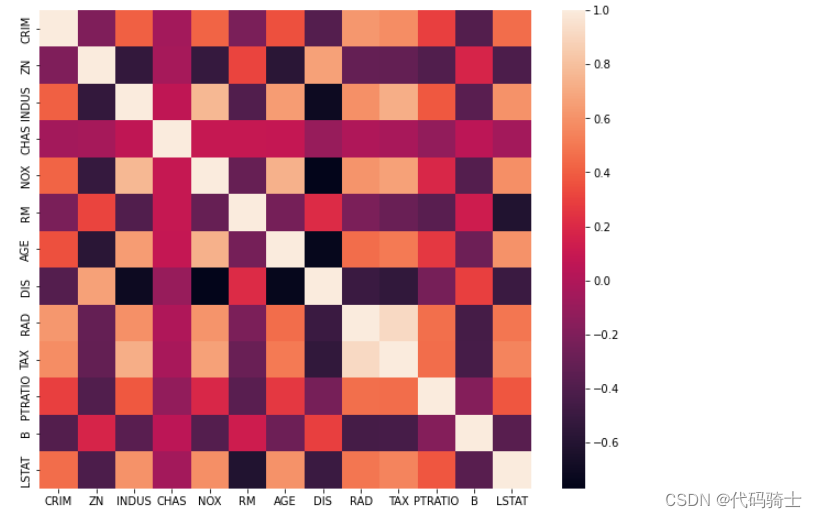
（3）使用VIF


# Import library for VIF (方差扩大因子)
from statsmodels.stats.outliers_influence import variance_inflation_factor
 
def vif(X):
 
    # Calculating VIF
    vif = pd.DataFrame()
    vif["variables"] = X.columns
    vif["VIF"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
 
    return(vif)

vif(X)

从中找寻vif最大的再从X中去除，每次去除一个都需要重新再计算vif。以此类推，直到剩余的各特征vif在标准范围之内即可。


X = X.drop('PTRATIO',axis=1)
vif(X)


X = X.drop('NOX',axis=1)
vif(X)


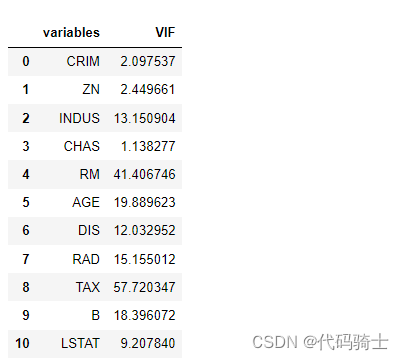
X = X.drop('TAX',axis=1)
vif(X)


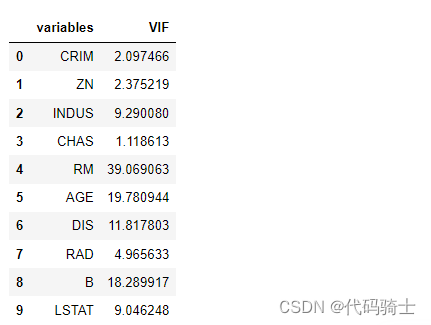
X = X.drop('RM',axis=1)
vif(X)


X = X.drop('AGE',axis=1)
vif(X)


X = X.drop('B',axis=1)
vif(X)

五、Ridge,Lasso Regression岭回归，Lasso回归解决线性回归的Overfitting过度拟合

Ridge回归和Lasso回归都是线性回归的扩展方法，它们都在试图解决线性回归的一些问题，如过拟合等。

在标准线性回归的基础上，岭回归（Ridge regression）通过在损失函数中加入L2正则化项进行修改，即应用α系数的Σ（系数的平方值），以控制正则化强度。较大的α值意味着更强的正则化（过拟合程度降低但可能会变为欠拟合！），较小的值意味着弱正则化（过度拟合）。

同样，Lasso回归也对标准线性回归做了修改，但它使用的是L1正则化项。此外，Lasso回归还有两个特性：稀疏性和选择特征的能力。在梯度下降时，Lasso回归求得的梯度只有1和-1两种值，所以每次更新步长它都在稳步向前前进。这使得Lasso回归能够将与相应变量无关系的变量系数缩减为0，从而实现特征选择。

总的来说，Ridge回归和Lasso回归都通过在损失函数中添加正则化项来改进线性回归，以防止过拟合并提高模型的准确性。不过，它们在如何处理这些正则化项以及如何进行特征选择上有所不同。

过拟合：

过拟合是一种在机器学习中不希望出现的现象，它发生在模型过于贴合训练数据，以至于损失过拟合是一种在机器学习中不希望出现的现象，它发生在模型过于贴合训练数据，以至于损失函数在验证集或新数据上表现不佳，从而导致模型的泛化性能下降。换句话说，过拟合模型对训练数据的预测准确率很高，但对新的、未知的数据的预测准确率却很低。

过拟合的原因可能包括：模型过于复杂、训练数据量不足、特征数量过多等。解决过拟合的方法通常包括：增加数据量、减少特征数量、使用正则化方法（如Ridge回归和Lasso回归）以及使用集成学习等。

如何通过Ridge回归和Lasso回归判断模型已经不再过拟合了？

判断Ridge回归和Lasso回归模型是否过拟合，主要依赖于一些评估指标。对于Ridge回归，可以使用均方误差（MSE）或均方根误差（RMSE）等度量来评估模型的好坏。如果这些值较小，说明模型的预测效果较好，可能并未发生过拟合。另外，还可以通过观察岭线图来分析模型的复杂度与误差之间的关系。

对于Lasso回归，同样可以使用MSE或RMSE等度量标准进行评估。不同的是，Lasso回归会将一些系数压缩至为零，这可以帮助我们理解哪些特征对模型预测结果的影响较大。

正则化参数alpha在Ridge回归和Lasso回归中都起着重要的作用。例如，在Ridge回归中，alpha是正则化参数，其值的大小会影响模型的复杂程度与误差之间的权衡。而在Lasso回归中，alpha的值会影响惩罚项与系数之和的大小，进而决定哪些特征的系数会被压缩为0。因此，选择合适的alpha值对于防止模型过拟合也非常关键。

岭回归公式及解析

Lasso回归公式及解析

应用案例（一）

1、导入函数库和数据集


import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
 
from sklearn.datasets import load_boston#波士顿房价预测数据集
 
boston=load_boston()#波士顿房价预测数据集

2、提取特征向量集


X=pd.DataFrame(boston['data'])
 
#添加索引列
X.columns=boston['feature_names']

3、提取响应变量集

y=boston.target

4、三种回归模型分析

（1）Linear Regression

使用K折交叉验证的方式进行模型评估

K折交叉验证（K-fold Cross Validation）是一种常用的模型评估方法，用于评估机器学习算法的性能。它将数据集分成K个子集，每次将其中一个子集作为测试集，其余的K-1个子集作为训练集。然后，重复K次这个过程，每次选择不同的子集作为测试集，最后计算K次测试结果的平均值作为模型的性能指标。

K折交叉验证的主要优点是可以有效地利用有限的数据集进行模型评估，同时避免了数据划分的随机性对评估结果的影响。但是，当数据集较小或者类别分布不均匀时，K折交叉验证可能会导致评估结果的不稳定。在这种情况下，可以尝试使用分层K折交叉验证（Stratified K-fold Cross Validation），在每个子集中保持类别的比例与整个数据集相同。


from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score
#cross_val_score是scikit-learn库中的一个函数，用于评估模型的性能。
#它通过将数据集分成k个子集，然后进行k次训练和验证，每次使用不同的子集作为验证集，最后计算模型的平均性能得分。
#就是k“fold”——k折交叉验证
linregressor=LinearRegression()
cvscore=cross_val_score(linregressor,X,y,cv=5)
#其中，cv参数表示交叉验证的折数，默认为5。scores是一个包含每次验证得分的数组。
#如有500个数据，分成5份，就是每份100个，每次取一份100个做测试集，另外400份做训练集
#重复进行五次，最后计算模型的平均性能得分。

cross_val_score是scikit-learn库中的一个函数，用于评估模型的性能。它通过将数据集分成k个子集，然后进行k次训练和验证，每次使用不同的子集作为验证集，最后计算模型的平均性能得分。

print(cvscore)

array([ 0.63919994,  0.71386698,  0.58702344,  0.07923081, -0.25294154])

mean_score = np.mean(cvscore)

print(mean_score)

0.3532759243958772

经过5折的交叉验证，线性回归模型性能的平均得分为0.3532759243958772，说明改数据对于一元线性回归模型效果并不理想。

虽然模型并未体现假设模型过拟合，但是如果出现过拟合，我们可以通过以下两种方式解决：

（2）Ridge Regression

Ridge

也被称为岭回归，是一种缩减（shrinkage）方法，用于控制线性回归模型中系数的大小。这种方法主要用于解决多重共线性问题和过拟合问题。与主成分回归等改变X的算法不同，Ridge回归通过添加一个L2正则化项，也就是对系数的大小进行惩罚，以防止过拟合。

在Ridge回归中，我们通常使用λ（或alpha）参数来控制正则化的强度。当λ增加时，惩罚项的权重也会增加，导致模型的系数缩小。相反，当λ减小时，惩罚项的权重也会减小，这可能导致模型的系数增大。

此外，Ridge回归和Lasso回归都是处理大量特征情况下创建简约模型的强大技术。这些技术可以应对大到足以引起计算硬件挑战的特征数量。总的来说，Ridge回归是一种强大且常用的机器学习工具，适用于许多现实生活的问题。

GridSearchCV

是一个用于超参数优化的交叉验证技术，它的主要功能是在指定的参数范围内，通过GridSearchCV是一个用于超参数优化的交叉验证技术，它的主要功能是在指定的参数范围内，通过网格搜索的方式找到一组最优参数，从而使得模型在验证集上的精度最高。这种方法主要用于寻找模型的最优超参数。

在使用GridSearchCV进行参数调优时，我们首先需要定义一个包含所有可能参数组合的字典或列表。然后，我们将这个字典或列表传递给GridSearchCV对象，并指定要评估的指标、要使用的交叉验证策略以及所需的迭代次数。GridSearchCV会按照预设的策略（如分层抽样或随机抽样）对数据进行分割，并在每次迭代中使用不同的参数组合训练模型，然后在验证集上计算指定指标的得分。最后，GridSearchCV会根据平均得分最高的参数组合来返回最优模型。


from sklearn.linear_model import Ridge
from sklearn.model_selection import GridSearchCV
 
ridge=Ridge()
parameters={'alpha':[1e-15,1e-10,1e-8,1e-3,1e-2,1,5,10,20,30,35,40,45,50,55,100,200,500,1000]}
ridgeregressor=GridSearchCV(ridge,parameters,cv=5)
ridgeregressor.fit(X,y)

GridSearchCV(cv=5, estimator=Ridge(),
             param_grid={'alpha': [1e-15, 1e-10, 1e-08, 0.001, 0.01, 1, 5, 10,
                                   20, 30, 35, 40, 45, 50, 55, 100, 200, 500,
                                   1000]})


print(ridgeregressor.best_params_)
print(ridgeregressor.best_score_)

{'alpha': 200}
0.49798762179623124

由模型评价指标看，明显高于上一个，但是岭回归模型需要找到合适的alpha值，当确定好一个模型参数后需要再继续找更合适更精细化的参数。


#ridge=Ridge()
parameters={'alpha':[160,170,180,190,200,210,230]}
ridgeregressor=GridSearchCV(ridge,parameters,cv=5)
ridgeregressor.fit(X,y)

GridSearchCV(cv=5, estimator=Ridge(),
             param_grid={'alpha': [160, 170, 180, 190, 200, 210, 230]})


print(ridgeregressor.best_params_)
print(ridgeregressor.best_score_)

{'alpha': 180}
0.4982367681072658

修改完参数后，模型的得分提升了大约0.001

（3）Lasso Regression

Lasso

全称Least Absolute Shrinkage and Selection Operator，是一种Lasso，全称Least Absolute Shrinkage and Selection Operator，是一种数据挖掘方法。它主要用在多元线性回归中，通过添加惩罚函数来不断压缩系数，从而达到精简模型的目的，以避免共线性和过拟合。此外，LASSO回归还有一个重要的特点就是能够实现对变量的筛选。当某个特征的系数为0时，该特征会被自动剔除，从而解决了逐步回归stepwise前进、后退变量筛选方法中的一些问题。

从数学的角度来看，Lasso回归的原理与岭回归类似，都是在目标函数后加了一个正则化项。但是Ridge回归使用的是L2正则化，而Lasso回归使用的则是L1正则化。

总的来说，Lasso回归提供了一种高效且灵活的解决方案，既可以避免模型过拟合，又可以解决变量选择的问题，因此在诸如基因组学、影像学等需要处理小样本数据的领域中，Lasso回归有着广泛的应用。


from sklearn.linear_model import Lasso
from sklearn.model_selection import GridSearchCV
lasso=Lasso()
parameters={'alpha':[1e-15,1e-10,1e-8,1e-3,1e-2,1,5,10,20,30,35,40,45,50,55,100,200,300,500]}
lassoregressor=GridSearchCV(lasso,parameters,cv=5)
 
lassoregressor.fit(X,y)
print(lassoregressor.best_params_)
print(lassoregressor.best_score_)

{'alpha': 1}
0.431848787926522

从以上分析可以看出Lasso回归模型可以确定一个alpha值1，和模型评价指标值为0.43，但是通过确定更加精确alpha值，可以调整出更好的模型。

Lasso(alpha=1, fit_intercept=False, tol=0.00000000000001,max_iter=10000000000000, positive=True)

Lasso(alpha=1, fit_intercept=False, max_iter=10000000000000, positive=True,
      tol=1e-14)

除了使用交叉验证（CV）的方式让算法自动帮我们训练并模型好坏外，还可以使用传统的拆分数据集的方法对Ridge和Lasso模型进行训练，


from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

对比模型测试集预测


prediction_lasso=lassoregressor.predict(X_test)
prediction_ridge=ridgeregressor.predict(X_test)

预测结果绘图


import seaborn as sns
 
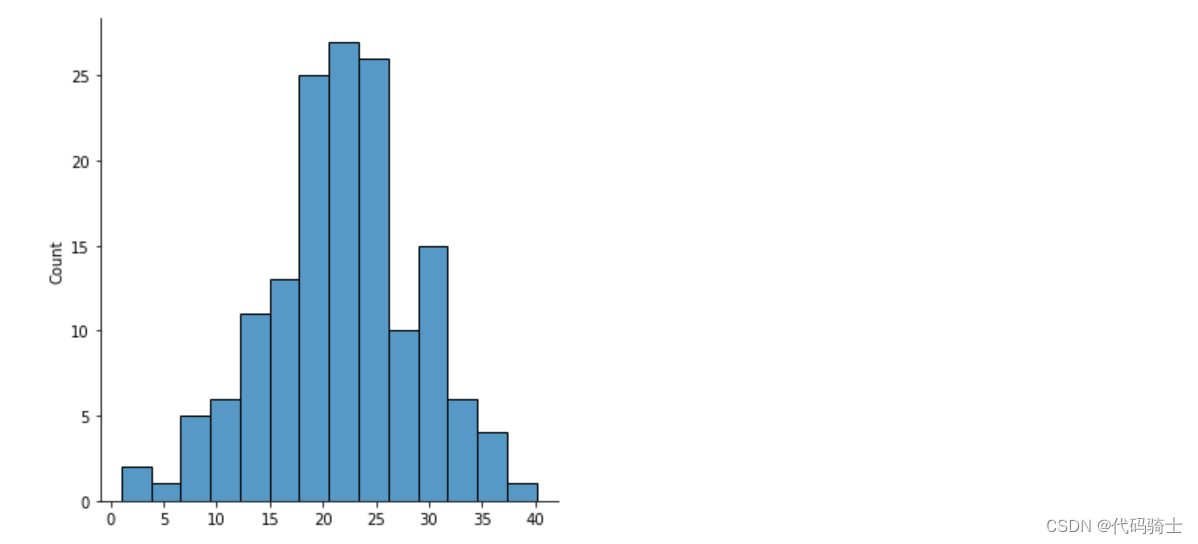
#sns.kdeplot(prediction_lasso)
sns.histplot(prediction_lasso)


import seaborn as sns
 
#sns.kdeplot(prediction_ridge)
sns.displot(prediction_ridge)

六、Logistic Regression逻辑回归应用

逻辑回归（Logistic Regression）是一种广义的线性回归分析模型，同时也属于机器学习中的监督学习。尽管其名称中含有"回归"二字，实际上它主要被用于解决二分类问题，例如预测客户是否会购买某个商品，借款人是否会违约等等。此外，逻辑回归也可以应用于多分类问题。

在处理这类问题时，逻辑回归会估计某种事物的可能性，例如某用户购买某商品的可能性，某病人患有某种疾病的可能性，以及某广告被用户点击的可能性等。但需要注意的是，这里提到的是“可能性”，而非数学上的“概率”，因此逻辑回归的结果并非数学定义的概率值。

逻辑回归在线性回归的基础上，套用了一个逻辑函数，将线性回归的结果从(-∞，∞)映射到(0,1)。具体来说，如果p表示某个样本属于正类的概率，那么这个样本被分为正类当且仅当p>0.5。否则，这个样本被分为负类。而我们的任务就是根据给定的样本特征x，求解出这个概率p。在逻辑回归中，我们通常使用sigmoid函数作为逻辑函数，将线性回归的结果映射到(0,1)区间。sigmoid函数的公式为：g(z) = 1 / (1 + e^-z)，其中z = w^Tx + b是线性回归的结果。通过这种方式，逻辑回归成功地解决了线性模型值域范围过大的问题。总的来说，逻辑回归是一种强大且实用的分类算法，其原理简单易懂，计算效率高，而且具有很好的可解释性。

逻辑回归公式及解析

应用案例（一）

1、导入函数库


import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
 
from sklearn.linear_model import LogisticRegression#逻辑回归函数
from sklearn.model_selection import train_test_split#切分数据集（训、测）
from sklearn.metrics import confusion_matrix#混淆矩阵

2、加载数据集


#二分类数据——证明是否有糖尿病 
data=pd.read_csv('./kaggle-data/diabetes.csv')

3、划分数据集为X，y


X=data.iloc[:,:-1]#特征集
 
y=data.iloc[:,-1]#响应集

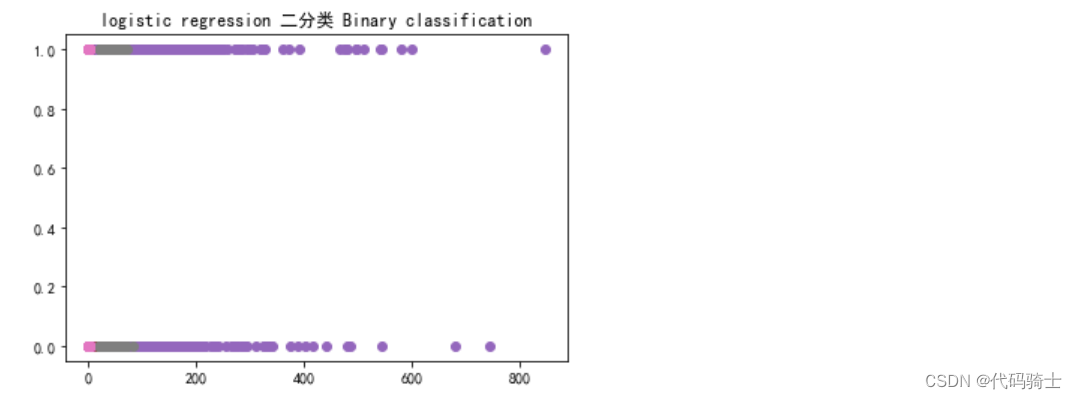
4、绘制二分类图像


plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
 
plt.plot(X,y,'o')
plt.title('logistic regression 二分类 Binary classification') #二分类 Binary classification
plt.show()

5、切分数据集为——trian、test集

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

6、创建逻辑回归模型并训练


logregression=LogisticRegression()
 
logregression.fit(X_train,y_train)

修改Warning


#Increase the number of iterations (max_iter) or scale the data
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
                   intercept_scaling=1, l1_ratio=None, max_iter=10000,
                   multi_class='auto', n_jobs=None, penalty='l2',
                   random_state=None, solver='lbfgs', tol=0.0001, verbose=0,
                   warm_start=False)

LogisticRegression(max_iter=10000)

y_predict=logregression.predict(X_test)

print('Accuracy of logistic regression classifier on diabetes: {:.3f}'.format(logregression.score(X_test, y_test)))

Accuracy of logistic regression classifier on diabetes: 0.779

准确率

准确率（Accuracy）是一个主要的分类任务评估指标，它衡量的是预测正确的样本数量占总样本数量的比例。更具体来说，如果你有n个样本，其中真正例（TP）、真反例（TN）、假正例（FP）和假反例（FN）分别为a、b、c和d，那么准确率的计算公式就是 (a+d)/(a+b+c+d)。

然而，需要注意的是，准确率并不是所有情况下都适用的评价指标。例如，在类别严重不平衡的情况下，即使模型将所有样本都预测为多数类别，其准确率也可能会非常高。因此，在这种情况下，我们可能需要结合其他指标如精确率（Precision）、召回率（Recall）或F1 Score等来进行更全面的评估。

logregression.score(X_test, y_test) #(141+39)/(141+39+16+35)=180/231

0.7792207792207793


#混淆矩阵
confusion_matrix(y_test,y_predict)

array([[141,  16],
       [ 35,  39]], dtype=int64)

混淆矩阵

混淆矩阵，也被称为可能性矩阵或错误矩阵，是机器学习中用于评估分类模型预测结果的重要工具。它以矩阵的形式，根据真实的类别与分类模型预测的类别，对数据集中的记录进行汇总。

在具体形式上，混淆矩阵通常为一个方阵，其大小为（真实值，预测值）或者（预测值，真实值）。这样的布局可以帮助我们更清晰地看出预测集与真实集中混合的一部分。在这个矩阵中，每一行代表实际类别，每一列代表预测类别。而矩阵的每个单元格则包含了在该实际类别和预测类别下的样本数量。

通过混淆矩阵，我们可以计算出诸如准确度、精确度和召回率等评估指标，全面地了解模型在不同类别上的性能。此外，在某些应用场景中（如医疗诊断、欺诈检测等），不同类型的错误（False Positives 和 False Negatives）可能具有不同的成本或严重性。此时，混淆矩阵就可以帮助我们更细致地评估这些成本。

混淆矩阵：

在二分类问题中，True Positives（TP），False Positives（FP），True Negatives（TN）和False Negatives（FN）是混淆矩阵的四个基本组成部分，这些都是用来评估模型预测结果的重要指标。

        - True Positives（TP，真正例）：预测为正，实际也为正。这指的是模型正确地将正类判断为正类的情况。
        - False Positives（FP，假正例）：预测为正，但实际为负。这指的是模型错误地将负类判断为正类的情况，也被称为误报。
        - True Negatives（TN，真负例）：预测为负，实际也为负。这指的是模型正确地将负类判断为负类的情况。
        - False Negatives（FN，假负例）：预测为负，但实际为正。这指的是模型错误地将正类判断为负类的情况，也被称为漏报。

这些指标有助于我们全面理解模型的预测性能，例如精确度、召回率等重要评价指标都可以通过这些基础指标计算得出。


#输出混淆矩阵的计算值
from sklearn.metrics import classification_report
 
print(classification_report(y_test, y_predict))  
 
#precision=141/(141+35) 39/(39+16)
#recall=141/(141+16) 39/(35+39)

precision    recall  f1-score   support

           0       0.80      0.90      0.85       157
           1       0.71      0.53      0.60        74

    accuracy                           0.78       231
   macro avg       0.76      0.71      0.73       231
weighted avg       0.77      0.78      0.77       231

print(logregression.coef_)

[[ 0.08528142  0.03447238 -0.01082115  0.00636555 -0.0013322   0.08852989
   0.73271533  0.02415024]]

print(logregression.intercept_)

[-8.605395]


#绘制ROC曲线
from sklearn.metrics import roc_auc_score
from sklearn.metrics import roc_curve
 
logrocauc = roc_auc_score(y_test, logregression.predict(X_test))
fpr, tpr, thresholds = roc_curve(y_test, logregression.predict_proba(X_test)[:,1])
plt.figure()
plt.plot(fpr, tpr, label='Logistic Regression (area = %0.3f)' % logrocauc)
plt.plot([0, 1], [0, 1],'r--')
plt.xlim([0.0, 1.05])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic')
plt.legend(loc="lower right")
#plt.savefig('Log_ROC')
plt.show()

ROC曲线主要用于评估分类器在不同阈值下对样本的识别能力，以及选择最佳的诊断界限值。具体来说，ROC曲线可以很容易地查出一个分类器在某个阈值时对样本的识别能力，同时，我们还可以借助ROC曲线选择出某一诊断方法最佳的诊断界限值。此外，ROC曲线也经常被用于评价某个或多个指标（如建立的模型或关键基因）对两类测试者（如患者和正常人）的分类及诊断效果。

在分析ROC曲线时，我们主要关注以下几个方面：
1. 对于随机抽取的正例和反例，ROC曲线越靠近左上角，就表明该诊断方法的准确性越高。反之，如果ROC曲线靠近右下角，则表明该方法的准确性较低。
2. ROC曲线下的面积（AUC），这个值介于0.1和1之间，作为一个数值来直观的评价分类器的好坏，AUC的值越大，说明分类器的性能越好。
3. 不同的ROC曲线之间的比较，当两个或多个模型的ROC曲线相交时，这些模型的AUC值是相等的。此时，我们就需要根据具体问题来进行分析：例如，当需要高灵敏度时，相交处上方的模型可能会更优于相交处下方的模型；反之，当需要高特异性时，相交处下方的模型可能会更优于相交处上方的模型。

ROC曲线的交点，即ROC曲线之间的交点，并没有特殊的意义。当两个或多个模型的ROC曲线相交时，这些模型的AUC值是相等的。此时，我们就需要根据具体问题来进行分析：例如，当需要高灵敏度（Sensitivity）值时，相交处上方的模型可能会更优于相交处下方的模型；反之，当需要高特异性（Specificity）值时，相交处下方的模型可能会更优于相交处上方的模型。

ROC曲线

ROC曲线，全称为Receiver Operating Characteristic curve，中文名“受试者工作特征曲线”，是一种常用于评估分类器性能的图形工具。该曲线在一个二维平面上绘制，横坐标为假正率（False Positive Rate, FPR），纵坐标为真正率（True Positive Rate, TPR）。

在具体应用中，我们通常会根据分类器在测试样本上的表现得到一个TPR和FPR点对，这个点对就可以映射到ROC平面上的一点。然后通过调整分类器在分类时的阈值，我们就可以得到一条经过原点(0,0)且斜率为1的曲线，这条曲线就被称为此分类器的ROC曲线。一般情况下，我们希望ROC曲线能够尽量地远离对角线，即位于 (0, 0)和 (1, 1)连线的上方，因为这意味着模型的分类效果越好。

此外，ROC曲线不仅可以帮助我们评价某个或多个指标对两类被试（如病人和健康人）分类/诊断的效果，还可以找到最佳的指标临界值使得分类效果最好。同时，我们还可以通过计算ROC曲线下的面积（AUC, Area under Curve），这个值介于0.1和1之间，作为一个数值来直观的评价分类器的好坏，AUC的值越大，说明分类器的性能越好。

logrocauc

0.7125580995007746

fpr

FPR，全称为False Positive Rate，中文意为假阳性率或误报率，表示实际为负例的样本被错误地预测为正例的概率。

array([0.        , 0.        , 0.        , 0.00636943, 0.00636943,
       0.01273885, 0.01273885, 0.01910828, 0.01910828, 0.02547771,
       0.02547771, 0.03184713, 0.03184713, 0.04458599, 0.04458599,
       0.07006369, 0.07006369, 0.07643312, 0.07643312, 0.08280255,
       0.08280255, 0.10191083, 0.10191083, 0.12101911, 0.12101911,
       0.13375796, 0.13375796, 0.1656051 , 0.1656051 , 0.18471338,
       0.18471338, 0.19745223, 0.19745223, 0.20382166, 0.20382166,
       0.22292994, 0.22292994, 0.24203822, 0.24203822, 0.26751592,
       0.26751592, 0.2866242 , 0.2866242 , 0.29299363, 0.29299363,
       0.29936306, 0.29936306, 0.31210191, 0.31210191, 0.33121019,
       0.33121019, 0.33757962, 0.33757962, 0.35031847, 0.35031847,
       0.3566879 , 0.3566879 , 0.36942675, 0.36942675, 0.41401274,
       0.41401274, 0.44585987, 0.44585987, 0.50318471, 0.50318471,
       0.52866242, 0.52866242, 0.59235669, 0.59235669, 0.6433121 ,
       0.6433121 , 0.89171975, 0.89171975, 1.        ])

tpr

TPR，全称为True Positive Rate，中文意为真阳性率、命中率或召回率，它表示实际为正例的样本中被正确预测为正例的概率。在具体应用中，例如在分类问题中，我们希望TPR尽量地大，FPR尽量地小，这样我们就可以更好地区分正例和负例。

array([0.        , 0.01351351, 0.04054054, 0.04054054, 0.05405405,
       0.05405405, 0.10810811, 0.10810811, 0.27027027, 0.27027027,
       0.2972973 , 0.2972973 , 0.32432432, 0.32432432, 0.44594595,
       0.44594595, 0.48648649, 0.48648649, 0.51351351, 0.51351351,
       0.52702703, 0.52702703, 0.55405405, 0.55405405, 0.56756757,
       0.56756757, 0.58108108, 0.58108108, 0.63513514, 0.63513514,
       0.64864865, 0.64864865, 0.66216216, 0.66216216, 0.67567568,
       0.67567568, 0.7027027 , 0.7027027 , 0.72972973, 0.72972973,
       0.74324324, 0.74324324, 0.75675676, 0.75675676, 0.77027027,
       0.77027027, 0.78378378, 0.78378378, 0.7972973 , 0.7972973 ,
       0.83783784, 0.83783784, 0.85135135, 0.85135135, 0.86486486,
       0.86486486, 0.87837838, 0.87837838, 0.90540541, 0.90540541,
       0.91891892, 0.91891892, 0.93243243, 0.93243243, 0.94594595,
       0.94594595, 0.95945946, 0.95945946, 0.97297297, 0.97297297,
       0.98648649, 0.98648649, 1.        , 1.        ])

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/小小林熬夜学编程/article/detail/101387