Java的 Map以及实现一个简单的红黑树

Map是Java中的一种键值对（Key-Value）数据结构，它提供了高效的键值对的存储和访问。在Java中，常见的Map实现类有HashMap、LinkedHashMap和TreeMap等。这些实现类在底层使用不同的数据结构来存储键值对，以提供不同的性能和特性。

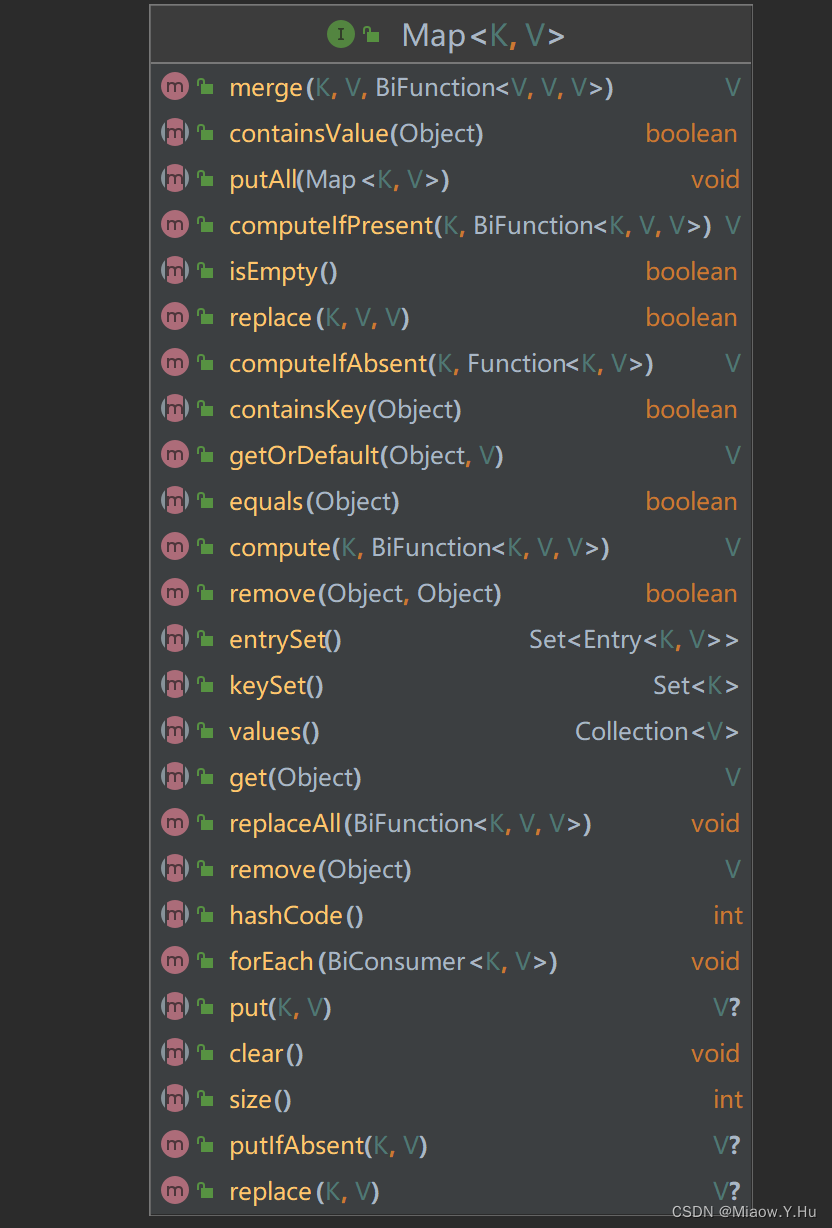
让我们看看官方介绍Map吧（采用机翻）

Map是将键映射到值的对象。map不能包含重复的键; 每个键最多只能映射到一个值。这个接口取代了Dictionary类，Dictionary类是一个完全抽象的类，而不是接口。

Map接口提供了三个集合视图，它们允许将映射的内容视为一组键、一组值或一组键-值映射。映射的顺序定义为映射集合视图上的迭代器返回其元素的顺序。一些类似实现，比如TreeMap类，对它们的顺序做出了特定的保证;其他类，如HashMap类，则不需要。

注意:如果使用可变对象作为映射键，必须非常小心。如果对象的值以影响相等比较的方式更改，而该对象是映射中的键，则不指定映射的行为。这种禁止的一个特殊情况是，不允许map将自身包含为键。虽然允许映射将自身包含为一个值，但建议非常小心。

equals和hashCode方法不再在这样的映射上得到很好的定义。

所有通用的map实现类都应该提供两个“标准”构造函数:

1. 创建空映射的void(无参数)构造函数，
2. 具有单个map类型参数的构造函数，它创建具有与其参数相同的键值映射的新映射。

实际上，后一种构造函数允许用户复制任何映射，生成所需类的等效映射。没有办法强制执行这个建议(因为接口不能包含构造函数)，但是JDK中的所有通用映射实现都遵循这个建议。该接口中包含的“破坏性”方法，即修改其操作的映射的方法，被指定为在该映射不支持该操作时抛出UnsupportedOperationException。如果是这种情况，如果调用对映射没有影响，这些方法可能(但不是必需)抛出UnsupportedOperationException。

例如，在不可修改的映射上调用putAll(Map)方法，如果要“叠加”其映射的映射为空，则可能(但不是必需的)抛出异常。一些映射实现对它们可能包含的键和值有限制。例如，有些实现禁止空键和空值，有些实现对其键的类型有限制。尝试插入不符合条件的键或值将引发未检查异常，通常为NullPointerException或ClassCastException。试图查询是否存在不符合条件的键或值可能会抛出异常，或者简单地返回false;有些实现将展示前一种行为，有些将展示后一种行为。更一般地说，尝试对不符合条件的键或值进行操作，其完成后不会导致在映射中插入不符合条件的元素，可能会抛出异常，也可能成功，这取决于实现的选择。这种异常在该接口的规范中被标记为“可选的”。

Collections Framework接口中的许多方法都是根据equals方法定义的。例如，containsKey(Object key)方法的规范说:“当且仅当此映射包含键k的映射使得(key==null ?)K ==null: key.equals(K))。”此规范不应被解释为暗示调用Map。带有非空参数key的containsKey将导致对任何键k调用key.equals(k)。实现可以自由地实现优化，从而避免equals调用，例如，首先比较两个键的哈希码。(Object.hashCode()规范保证两个哈希码不相等的对象不能相等。)更一般地说，只要实现者认为合适，各种集合框架接口的实现可以自由地利用底层对象方法的指定行为。一些执行递归遍历map的map操作可能会失败，对于map直接或间接包含自身的自引用实例可能会出现异常。这包括clone()、equals()、hashCode()和toString()方法。实现可以选择性地处理自引用场景，但是大多数当前实现都不这样做。

Map的特点

• 键唯一性：Map中的键是唯一的，每个键只能对应一个值。
• 无序性：Map中的键值对是无序的，插入顺序不会影响键值对的存储和访问顺序。
• 键和值的映射关系：每个键都与一个值相关联，通过键可以获取对应的值。
• 允许空键和空值：Map允许使用null作为键和值。
• 可变性：Map是可变的数据结构，可以动态地添加、修改和删除键值对。

Map的实现方式

• HashMap使用哈希表（Hash Table）实现，通过哈希函数将键映射到数组索引，以实现快速的插入、查找和删除操作。它提供了O(1)的平均时间复杂度。
• LinkedHashMap在HashMap的基础上，使用双向链表维护插入顺序，以保持键值对的迭代顺序。
• TreeMap使用红黑树（Red-Black Tree）实现，以保持键的有序性。它提供了O(log n)的时间复杂度。

Map的缺点

• 性能开销：相比于数组或列表，Map的性能开销较大。由于需要维护键的唯一性和映射关系，以及可能的哈希冲突等，Map的操作通常比较耗时。
• 内存占用：Map需要维护额外的数据结构来存储键值对的映射关系，这会占用一定的内存空间。
• 无序性：虽然Map提供了键值对的存储和访问，但是它们是无序的。如果需要有序性，可能需要使用其他数据结构。

示例：

将Map对象转换为List对象

import java.util.ArrayList;
import java.util.List;
import java.util.Map;

public class MapToListExample {
    public static void main(String[] args) {
        // 创建一个Map对象
        Map<String, Integer> map = Map.of("A", 1, "B", 2, "C", 3);

        // 将Map对象转换为List对象
        List<Map.Entry<String, Integer>> list = new ArrayList<>(map.entrySet());

        // 打印转换后的List对象
        for (Map.Entry<String, Integer> entry : list) {
            System.out.println(entry.getKey() + " : " + entry.getValue());
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

将HashMap的键值对结构转换为数组对象结构

import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;

public class HashMapToArrayExample {
    public static void main(String[] args) {
        // 创建一个HashMap对象
        Map<String, Integer> hashMap = new HashMap<>();
        hashMap.put("A", 1);
        hashMap.put("B", 2);
        hashMap.put("C", 3);

        // 将HashMap的键值对结构转换为数组对象结构
        List<MyObject> array = new ArrayList<>();
        for (Map.Entry<String, Integer> entry : hashMap.entrySet()) {
            MyObject obj = new MyObject(entry.getKey(), entry.getValue());
            array.add(obj);
        }

        // 打印转换后的数组对象
        for (MyObject obj : array) {
            System.out.println(obj.getKey() + " : " + obj.getValue());
        }
    }
}

class MyObject {
    private String key;
    private Integer value;

    public MyObject(String key, Integer value) {
        this.key = key;
        this.value = value;
    }

    public String getKey() {
        return key;
    }

    public Integer getValue() {
        return value;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

实现一个简易版本的红黑树

package com.xh.Map;

/**
 * @author HWZ
 * @date 2024年03月07日 11:01
 * @description
 */
public class RedBlackTree<K extends Comparable<K>, V> {
    private static final boolean RED = true;
    private static final boolean BLACK = false;

    private Node root;

    private class Node {
        private K key;
        private V value;
        private Node left, right;
        private boolean color;

        public Node(K key, V value) {
            this.key = key;
            this.value = value;
            this.color = RED;
        }
    }

    /**
     * 向红黑树中插入键值对
     * @param key 键
     * @param value 值
     */
    public void put(K key, V value) {
        root = put(root, key, value);
        root.color = BLACK;
    }

    private Node put(Node node, K key, V value) {
        if (node == null) {
            return new Node(key, value);
        }

        int cmp = key.compareTo(node.key);
        if (cmp < 0) {
            node.left = put(node.left, key, value);
        } else if (cmp > 0) {
            node.right = put(node.right, key, value);
        } else {
            node.value = value;
        }

        if (isRed(node.right) && !isRed(node.left)) {
            node = rotateLeft(node);
        }
        if (isRed(node.left) && isRed(node.left.left)) {
            node = rotateRight(node);
        }
        if (isRed(node.left) && isRed(node.right)) {
            flipColors(node);
        }

        return node;
    }

    /**
     * 删除红黑树中指定键的节点
     * @param key 键
     */
    public void delete(K key) {
        if (!contains(key)) {
            return;
        }

        if (!isRed(root.left) && !isRed(root.right)) {
            root.color = RED;
        }

        root = delete(root, key);
        if (root != null) {
            root.color = BLACK;
        }
    }

    private Node delete(Node node, K key) {
        if (key.compareTo(node.key) < 0) {
            if (!isRed(node.left) && !isRed(node.left.left)) {
                node = moveRedLeft(node);
            }
            node.left = delete(node.left, key);
        } else {
            if (isRed(node.left)) {
                node = rotateRight(node);
            }
            if (key.compareTo(node.key) == 0 && (node.right == null)) {
                return null;
            }
            if (!isRed(node.right) && !isRed(node.right.left)) {
                node = moveRedRight(node);
            }
            if (key.compareTo(node.key) == 0) {
                Node min = findMin(node.right);
                node.key = min.key;
                node.value = min.value;
                node.right = deleteMin(node.right);
            } else {
                node.right = delete(node.right, key);
            }
        }
        return balance(node);
    }

    private Node deleteMin(Node node) {
        if (node.left == null) {
            return null;
        }

        if (!isRed(node.left) && !isRed(node.left.left)) {
            node = moveRedLeft(node);
        }

        node.left = deleteMin(node.left);
        return balance(node);
    }

    /**
     * 判断红黑树中是否包含指定键
     * @param key 键
     * @return 是否包含指定键
     */
    public boolean contains(K key) {
        return get(key) != null;
    }

    /**
     * 根据键查找红黑树中的值
     * @param key 键
     * @return 值
     */
    public V get(K key) {
        Node node = root;
        while (node != null) {
            int cmp = key.compareTo(node.key);
            if (cmp < 0) {
                node = node.left;
            } else if (cmp > 0) {
                node = node.right;
            } else {
                return node.value;
            }
        }
        return null;
    }

    /**
     * 更新红黑树中指定键的值
     * @param key 键
     * @param value 值
     */
    public void update(K key, V value) {
        if (contains(key)) {
            put(key, value);
        }
    }

    private boolean isRed(Node node) {
        if (node == null) {
            return false;
        }
        return node.color == RED;
    }

    private Node rotateLeft(Node node) {
        if (node == null || node.right == null) {
            return node;
        }
        Node x = node.right;
        node.right = x.left;
        x.left = node;
        x.color = node.color;
        node.color = RED;
        return x;
    }

    private Node rotateRight(Node node) {
        Node x = node.left;
        node.left = x.right;
        x.right = node;
        x.color = node.color;
        node.color = RED;
        return x;
    }

    private void flipColors(Node node) {
        node.color = RED;
        node.left.color = BLACK;
        node.right.color = BLACK;
    }

    private Node moveRedLeft(Node node) {
        flipColors(node);
        if (isRed(node.right.left)) {
            node.right = rotateRight(node.right);
            node = rotateLeft(node);
            flipColors(node);
        }
        return node;
    }

    private Node moveRedRight(Node node) {
        flipColors(node);
        if (isRed(node.left.left)) {
            node = rotateRight(node);
            flipColors(node);
        }
        return node;
    }

    private Node balance(Node node) {
        if (isRed(node)) {
            node = rotateLeft(node);
        }
        if (isRed(node.left) && isRed(node.left.left)) {
            node = rotateRight(node);
        }
        if (isRed(node.left) && isRed(node.right)) {
            flipColors(node);
        }
        return node;
    }

    private Node findMin(Node node) {
        while (node.left != null) {
            node = node.left;
        }
        return node;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236

这个简易版本的红黑树实现包括了插入、删除、查找和修改操作。红黑树的节点使用内部类Node表示，包含了键、值、左子节点、右子节点和颜色属性。

插入操作使用递归实现，并根据红黑树的性质进行旋转和颜色翻转来保持树的平衡性。删除操作也使用递归实现，并根据不同情况进行旋转和颜色翻转来保持树的平衡性。

查找操作根据键的比较逐级向下搜索，直到找到匹配的键或搜索到叶子节点为止。修改操作先判断是否包含指定的键，如果包含则调用插入操作来更新键对应的值。

注意，这只是一个简易版本的红黑树实现，并没有考虑到所有的边界情况和优化。在实际应用中，我们更加建议使用Java标准库中的TreeMap来实现红黑树，它提供了更完善和高效的实现。

上述红黑树代码的测试：

public class RedBlackTreeTest {
    public static void main(String[] args) {
        RedBlackTree<Integer, String> tree = new RedBlackTree<>();

        // 插入操作
        tree.put(5, "Value 5");
        tree.put(2, "Value 2");
        tree.put(8, "Value 8");
        tree.put(1, "Value 1");
        tree.put(4, "Value 4");
        tree.put(7, "Value 7");
        tree.put(9, "Value 9");

        // 查找操作
        System.out.println(tree.get(4)); // 输出: Value 4
        System.out.println(tree.get(10)); // 输出: null

        // 修改操作
        tree.update(4, "New Value 4");
        System.out.println(tree.get(4)); // 输出: New Value 4

        // 删除操作
         tree.delete(2);
        System.out.println(tree.contains(2)); // 输出: false
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26