蚁群算法（Ant Colony Optimization）

一、蚁群算法

蚁群算法是一种智能优化算法，通过蚁群优化求解复杂问题，ACO在离散优化问题方面有比较好的优越性。       
蚁群算法是一种用来寻找优化路径的概率型算法。它由Marco Dorigo于1992年在他的博士论文中提出，其灵感来源于蚂蚁在寻找食物过程中发现路径的行为。
1
2

二、算法背景

单只蚂蚁的行为及其简单，行为数量在10种以内，但成千上万只蚂蚁组成的蚁群却能拥有巨大的智慧，这离不开它们信息传递的方式——信息素。
蚂蚁在行走过程中会释放一种称为“信息素”的物质，用来标识自己的行走路径。在寻找食物的过程中，根据信息素的浓度选择行走的方向，并最终到达食物所在的地方。
信息素会随着时间的推移而逐渐挥发。
在一开始的时候，由于地面上没有信息素，因此蚂蚁们的行走路径是随机的。蚂蚁们在行走的过程中会不断释放信息素，标识自己的行走路径。随着时间的推移，有若干只蚂蚁找到了食物，此时便存在若干条从洞穴到食物的路径。由于蚂蚁的行为轨迹是随机分布的，因此在单位时间内，短路径上的蚂蚁数量比长路径上的蚂蚁数量要多，从而蚂蚁留下的信息素浓度也就越高。这为后面的蚂蚁们提供了强有力的方向指引，越来越多的蚂蚁聚集到最短的路径上去。
（1）高度结构化的组织——虽然蚂蚁的个体行为极其简单，但由个体组成的蚁群却构成高度结构化的社会组织，蚂蚁社会的成员有分工，有相互的通信和信息传递。
（2）自然优化——蚁群在觅食过程中，在没有任何提示下总能找到从蚁巢到食物源之间的最短路径；当经过的路线上出现障碍物时，还能迅速找到新的最优路径。
（3）信息正反馈——蚂蚁在寻找食物时，在其经过的路径上释放信息素（外激素）。蚂蚁基本没有视觉，但能在小范围内察觉同类散发的信息素的轨迹，由此来决定何去何从，并倾向于朝着信息素强度高的方向移动。
（4）自催化行为——某条路径上走过的蚂蚁越多，留下的信息素也越多（随时间蒸发一部分），后来蚂蚁选择该路径的概率也越高。
1
2
3
4
5
6
7
8

三、算法基本思想

（1）根据具体问题设置多只蚂蚁，分头并行搜索。
（2）每只蚂蚁完成一次周游后，在行进的路上释放信息素，信息素量与解的质量成正比。
（3）蚂蚁路径的选择根据信息素强度大小（初始信息素量设为相等），同时考虑两点之间的距离，采用随机的局部搜索策略。这使得距离较短的边，其上的信息素量较大，后来的蚂蚁选择该边的概率也较大。
（4）每只蚂蚁只能走合法路线（经过每个城市1次且仅1次），为此设置禁忌表来控制。
（5）所有蚂蚁都搜索完一次就是迭代一次，每迭代一次就对所有的边做一次信息素更新，原来的蚂蚁死掉，新的蚂蚁进行新一轮搜索。
（6）更新信息素包括原有信息素的蒸发和经过的路径上信息素的增加。
（7）达到预定的迭代步数，或出现停滞现象（所有蚂蚁都选择同样的路径，解不再变化），则算法结束，以当前最优解作为问题的最优解。
1
2
3
4
5
6
7

四、表示方式

4.1 参数表示

4.2 计算公式

五、算法步骤

六、蚁群算法解决旅行商问题

6.1 问题提出

6.2 实例

假设5个城市的TSP问题，然由于某种原因，城市道路均是单行道，即A->B和B->A的距离不相同，也就是说这是一个不对称的TSP问题。现在城市距离信息如下表：
1

6.3 参数设置—初始化

6.4 计算步骤

根据初始化信息素得到初始化信息素矩阵
1

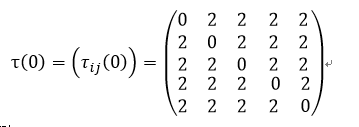
启发式矩阵
1

对每个节点求对应的参数，首先求第一次迭代第一只蚂蚁：
1

第一次迭代第二只蚂蚁：
1

第一次迭代第三只蚂蚁：
1

第一次迭代第四只蚂蚁：
1

第一次迭代第五只蚂蚁：
1

第一次迭代完成，更新信息素矩阵，信息素挥发系数为0.5。
1

至此，第一代蚂蚁全部周游完成，重新随机生成第二代蚂蚁进行迭代。
第二次迭代第一只蚂蚁：
1
2

第二次迭代第二只蚂蚁：
1

第二次迭代第三只蚂蚁：
1

第二次迭代第四只蚂蚁：
1

第二次迭代第五只蚂蚁：
1

6.5 结论

当出现停滞现象的时候，说明已经得到最优解，算法结束。
我们发现在第二次迭代的时候，五只蚂蚁走的是同一条路，所以算法收敛结束。    
最优路径A->E->D->C->B->A, 最优路径的距离为9.
1
2
3

七、蚁群算法特点

蚁群算法是一种基于多主体的智能算法，不是单个蚂蚁行动，而是多个蚂蚁同时搜索，具有分布式的协同优化机制。
本质上属于随机搜索算法（概率算法），具有概率搜索的特征。
是一种全局搜索算法，能够有效地避免局部最优。
（1）较强的鲁棒性——稍加修改即可应用于其他问题；
（2）分布式计算——本质上具有并行性；
（3）易于与其他启发式算法结合。
1
2
3
4
5
6

转载自：
https://www.imooc.com/article/23910?block_id=tuijian_wz
http://www.dataguru.cn/article-11200-1.html
https://www.cnblogs.com/tao-alex/p/6094483.html