机器学习初学-RNN+CNN处理时序问题_采用rnn模型对1d时间序列进行分类

数据集New Earth | Kaggle

1 构建特征集和标签集

df_train = pd.read_csv('../input/new-earth/exoTrain.csv') # 导入训练集 
df_test = pd.read_csv('../input/new-earth/exoTest.csv') # 导入测试集 
from sklearn.utils import shuffle # 导入乱序工具 
df_train = shuffle(df_train)# 乱序训练集 
df_test = shuffle(df_test)# 乱序测试集
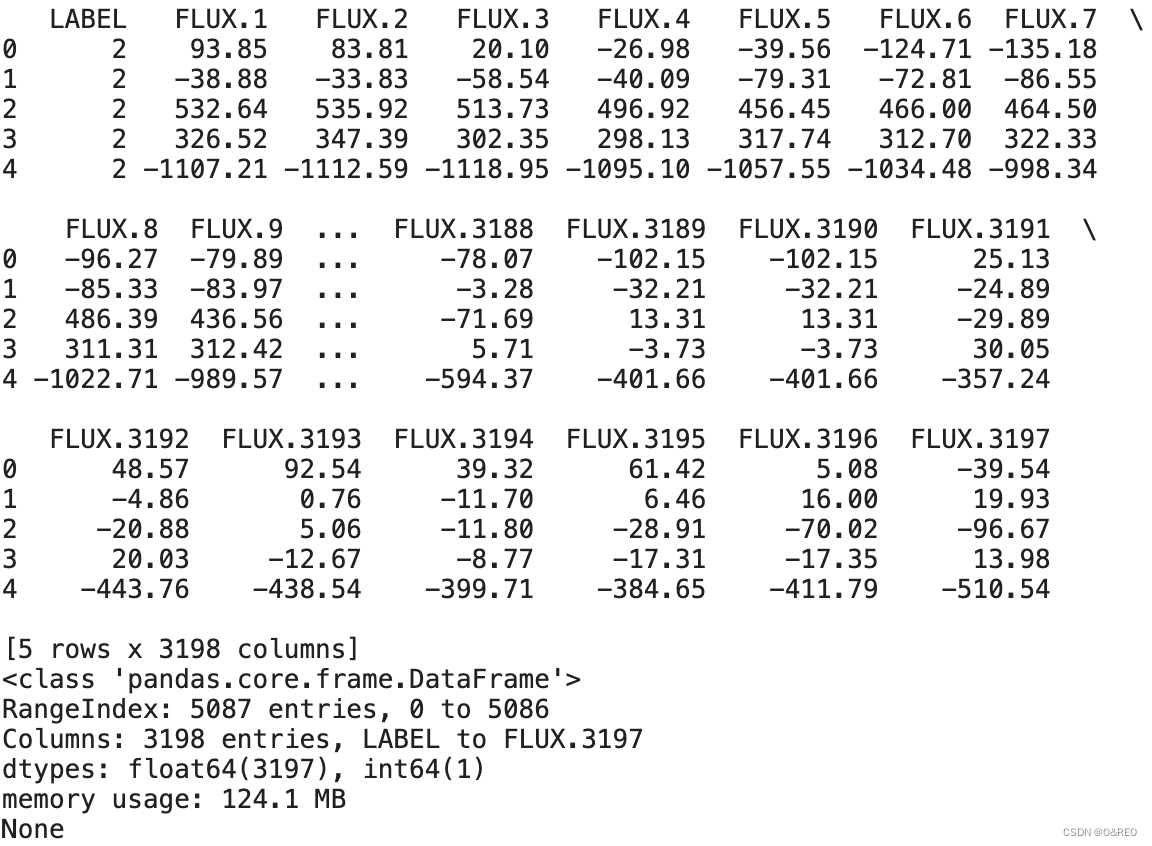
print(df_train.head())# 输入前几行数据
print(df_train.info())# 输入前几行数据

每一行代表一颗恒星，而每一列的含义如下:
 ■第1列，LABLE，恒星是否拥有行星的标签，2代表有行星，1代表无行星。 
 ■第2列～第3 198列，即FLUX.n字段，是科学家们通过开普勒天文望远镜记录的每一颗恒星在不同时间点的亮度，其中n代表不同时间点。

下面的代码将构建特征集和标签集，把第2列～第3 198列的数据都读入X特征集，第1列的数据都读入y标签集

在这个代码段中，`.iloc` 是 Pandas 库提供的方法，用于按照指定的行号或列号来选取数据。`iloc` 的用法是通过方括号 `[]` 内的索引值来指定要选择的行和列。

具体来说，方括号内的索引参数由两部分组成，用逗号分隔：

- 第一部分表示要选择的行范围，可以是单个整数、整数列表或布尔数组。`:` 表示选择所有行。例如，`[0]` 表示只选择第一行，`[1:5]` 表示选择从第二行到第五行（不包括第五行），`[True, False, True]` 表示选择第一行和第三行。

- 第二部分表示要选择的列范围，可以是单个整数、整数列表或布尔数组。与行范围类似，`: `表示选择所有列。例如，`[:, 1:]` 表示选择从第二列开始的所有列。

在给定的代码段中，`.iloc[:, 1:]` 表示选择所有行，从第二列开始的所有列，即构建特征集。`.iloc[:, 0]` 表示选择所有行的第一列，即构建标签集。

请注意，`.values` 是将 Pandas 数据结构转换为 NumPy 数组，以方便后续的数据处理和建模操作。 

在给定的代码段中，np.expand_dims() 函数用于在张量中添加一个新的轴/维度。

在这里， axis=2 的意思是在第二个维度（索引从0开始）上添加一个新的维度。这意味着 X_train 和 X_test 张量的维度会增加一个维度。

具体来说，假设 X_train 原本的形状是 (n_samples, n_features)，这意味着它是一个二维张量，其中 n_samples 是样本数，n_features 是特征数。通过执行 np.expand_dims(X_train, axis=2)，结果的形状将变为 (n_samples, n_features, 1)。新添加的维度大小为 1。

X_train = df_train.iloc[:, 1:].values # 构建特征集(训练集) 
y_train = df_train.iloc[:, 0].values # 构建标签集(训练集) 
X_test = df_test.iloc[:, 1:].values # 构建特征集(验证集) 
y_test = df_test.iloc[:, 0].values # 构建标签集(验证集) 
y_train = y_train - 1 # 标签转换成惯用的(0, 1)分类值 
y_test = y_test - 1 # 标签转换成惯用的(0, 1)分类值 
X_train = np.expand_dims(X_train, axis=2) # 张量升阶, 以满足序列数据集的要求 
X_test = np.expand_dims(X_test, axis=2) # 张量升阶, 以满足序列数据集的要求
print (X_train) # 输出训练集中的特征集 
print (y_train) # 输出训练集中的标签集
X_train.shape

输出显示张量形状为（5 087，3 197，1），符合时序数据结构的规则：5 087个样本，3 197个时戳，1维的特征（光线的强度）。因此，这些数据可以输入神经网络进行训练。

2 CNN组合RNN建模

通过一维卷积网络，即Conv1D层，组合循环神经网络层来处理序列数据。 Conv1D层接收形状为（样本，时戳或序号，特征） 的3D张量作为输入，并输出同样形状的3D张量。卷积窗口作用于时间轴（输入张量的第二个轴）上，此时的卷积窗口不是2D的，而是1D的。

 对于文本数据来说，如果窗口大小为5，也就是说每个段落以5个词为单位来扫描。不难发现，这样的扫描有利于发现词组、惯用语等。 对于时间序列数据来说，1D卷积也有其优势，因为速度更快。 

 因此产生了如下思路：使用一维卷积网络作为预处理步骤，把长序列提取成短序列，并把有用的特征交给循环神经网络来继续处理。 

下面的这段代码，就构建了一个CNN和RNN联合发挥作用的神经网络：

from keras.models import Sequential # 导入序贯模型 
from keras import layers # 导入所有类型的层 
from keras.optimizers import Adam # 导入优化器 
model = Sequential()# 序贯模型 
model.add(layers.Conv1D(32, kernel_size=10, strides=4, 
input_shape=(3197, 1)))# 1D CNN层 
model.add(layers.MaxPooling1D(pool_size=4, strides=2))# 池化层 
model.add(layers.GRU(256, return_sequences=True))# GRU层要足够大 
model.add(layers.Flatten())# 展平层 
model.add(layers.Dropout(0.4))# Dropout层 
model.add(layers.BatchNormalization())# 批标准化 
model.add(layers.Dense(1, activation='sigmoid'))# 分类输出层 
opt = Adam(learning_rate=0.0001, beta_1=0.9, beta_2=0.999, decay=0.01) 
model.compile(optimizer=opt,# 优化器 
loss = 'binary_crossentropy',# 交叉熵 
metrics=['acc'])# 准确率
model.summary()

1. `model.add(layers.Conv1D(32, kernel_size=10, strides=4, input_shape=(3197, 1)))`：
   这是一个一维卷积层（1D CNN），用于提取输入数据的特征。它具有 32 个滤波器（filters），每个滤波器的内核大小是 10，并使用步幅（strides）为 4 进行滑动。输入的形状是 (3197, 1)，表示输入数据具有 3197 个时间步和 1 个特征。
   
2. `model.add(layers.MaxPooling1D(pool_size=4, strides=2))`：
   这是一个池化层（MaxPooling1D），用于对卷积层输出的特征进行降采样。它使用大小为 4 的池化窗口进行最大池化操作，并使用步幅为 2 进行滑动。

3. `model.add(layers.GRU(256, return_sequences=True))`：
   这是一个 Gated Recurrent Unit（GRU）层，用于处理序列数据并捕捉长期依赖关系。它具有 256 个单元，并且设置 `return_sequences=True`，意味着输出将保留序列的维度。

GRU（Gated Recurrent Unit）层是一种循环神经网络（RNN）的变体，用于处理序列数据，并且在很多自然语言处理（NLP）和时间序列预测任务中取得了很好的效果。GRU 层的设计旨在克服传统的RNN存在的梯度消失和梯度爆炸问题，同时能够更好地捕捉长期依赖关系。

GRU 层包含一个可学习的门控结构，由两个门控单元组成：重置门和更新门。这些门控单元通过学习调节信息的流动和保留，从而控制了记忆单元的更新和忘记过去的信息。下面是对重置门和更新门的详细解释：

1. 重置门（Reset Gate）：
   重置门通过一个 sigmoid 激活函数来决定是否将过去的信息重置。它通过将当前输入与前一个隐藏状态进行相乘，来决定哪些过去的内容需要被遗忘。如果重置门的输出接近于0，它会让过去的信息被忘记，从而使网络更加专注于当前的输入。

2. 更新门（Update Gate）：
   更新门通过一个 sigmoid 激活函数来决定是否将过去的隐藏状态与当前的输入进行融合。它通过计算当前输入和前一个隐藏状态的相似性，来决定选择性更新过去的信息。如果更新门的输出接近于1，它会保留过去的隐藏状态几乎不变，从而将重要的信息传递到下一个时刻。

通过重置门和更新门的机制，GRU 层能够有效地控制信息的流动，处理长期依赖关系，并且相对于传统的RNN模型，GRU 层具有以下优势：

- 减轻梯度消失和梯度爆炸问题：GRU 层通过门控机制相对于传统的RNN层来说，更好地处理了梯度问题，使得训练更加稳定。
- 能够学习长期依赖关系：GRU 层通过重置门和更新门的控制，能够更好地捕捉和保留序列中的重要信息，从而更好地建模长期依赖关系。
- 参数较少：相比于 LSTM（Long Short-Term Memory）层，GRU 层的参数较少，计算效率也较高，因此在一些轻量级模型和资源受限的场景下更具优势。

综上所述，GRU 层是一种用于处理序列数据的循环神经网络的变体，通过具有重置门和更新门的机制，能够更好地捕捉长期依赖关系，并在许多序列建模任务中取得了很好的效果。

GRU（Gated Recurrent Unit）和LSTM（Long Short-Term Memory）对比

GRU和LSTM都是常见的循环神经网络（RNN）的变体，用于处理序列数据，特别在自然语言处理（NLP）和时间序列预测等任务中应用广泛。下面是 GRU 和 LSTM 之间的几个区别：

1. 架构复杂度：
   LSTM 层相对于 GRU 层在架构上更为复杂。LSTM 层包含输入门、遗忘门和输出门，而 GRU 层只有重置门和更新门。因此，LSTM 层的参数数量较多，计算复杂度也相对较高。相对而言，GRU 层参数更少，计算效率更高。

2. 学习长期依赖关系的能力：
   LSTM 和 GRU 层都通过门控机制来控制信息的流动，以解决传统 RNN 中长期依赖问题。LSTM 通过遗忘门和输入门的组合，可以有效地捕捉和保留长期记忆。GRU 通过重置门和更新门的机制，可以更好地处理长期依赖关系。一般来说，LSTM 在处理较长序列和复杂任务时可能具有更优的性能，而 GRU 则更适用于一些轻量级任务和资源受限的情况。

3. 训练效果和收敛速度：
   由于 LSTM 层的结构比 GRU 复杂，LSTM 可以更好地建模和捕捉复杂的序列模式和长期依赖关系。在某些任务中，LSTM 可能会比 GRU 产生更好的训练效果。然而，GRU 通常具有较快的收敛速度，因为它具有更少的参数，学习效率更高。

总结：作为循环神经网络的变体，LSTM 和 GRU 在处理序列数据时都具有优势，但在架构复杂度、学习长期依赖关系的能力以及训练效果和收敛速度等方面存在一些区别。选择使用 LSTM 还是 GRU 取决于具体的任务需求和数据特征，可以根据实际情况进行选择。

4. `model.add(layers.Flatten())`：
   这是一个展平层，用于将上一层输出的多维数据展平为一维数据。这样可以将序列数据转换为一维特征向量。

5. `model.add(layers.Dropout(0.4))`：
   这是一个 Dropout 层，用于在训练过程中随机失活一部分神经元，以减少过拟合的风险。参数 `0.4` 表示失活的比例为 40%。

6. `model.add(layers.BatchNormalization())`：
   这是一个批标准化层，用于对输入数据进行标准化处理，以加速训练收敛并提高模型的稳定性。批标准化（Batch Normalization）层的作用就是对网络的输入数据进行标准化处理，使得每个特征维度的均值接近0，标准差接近1。这样做的好处是可以更好地控制每一层网络的激活值分布，加速网络的收敛并提高模型的稳定性。

7. `model.add(layers.Dense(1, activation='sigmoid'))`：
   这是一个全连接层（Dense），用于进行分类的输出。它具有 1 个输出单元，使用 sigmoid 激活函数进行二分类。

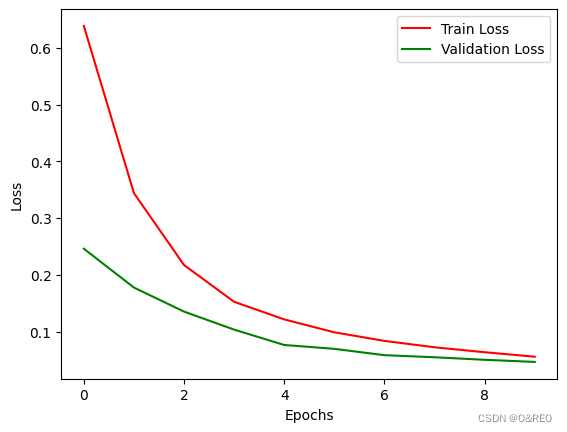
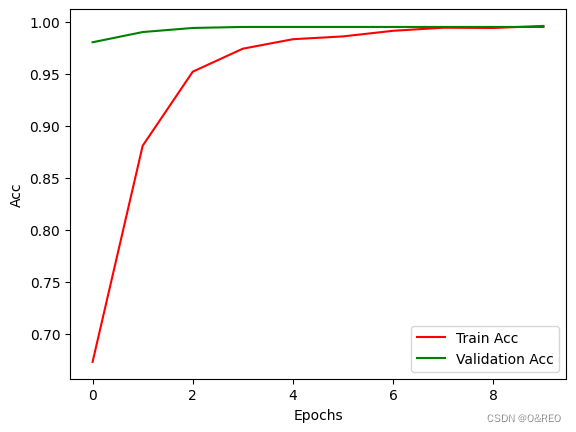
history = model.fit(X_train, y_train, # 指定训练集 
validation_split = 0.2, # 部分训练集数据拆分成验证集 
batch_size = 128, # 指定批量大小 
epochs = 10, # 指定轮次 
shuffle = True) # 乱序

 3 调整输出阈值

 通过accuracy指标来看模型看似很准但实际意义不大

当我们画图统计df_train df_test的‘LABLE’列中1和2的数量：

import seaborn as sns
import matplotlib.pyplot as plt
 
# 统计1和2的数量
label_counts = df_train['LABEL'].value_counts()
label_counts_test = df_test['LABEL'].value_counts()
 
# 设置Seaborn调色板
colors = sns.color_palette("cool", len(label_counts))
 
# 创建柱状图
plt.bar(label_counts.index, label_counts.values, color=colors)
 
# 设置标签和标题
plt.xlabel('TRAIN')
plt.ylabel('Count')
plt.title('Count of Labels')
 
# 设置横坐标刻度
plt.xticks(range(1, len(label_counts)+1))
 
# 显示图形
plt.show()
 
# 创建柱状图
plt.bar(label_counts_test.index, label_counts_test.values, color=colors)
 
# 设置标签和标题
plt.xlabel('TEST')
plt.ylabel('Count')
plt.title('Count of Labels')
 
# 设置横坐标刻度
plt.xticks(range(1, len(label_counts_test)+1))
 
# 显示图形
plt.show()

 

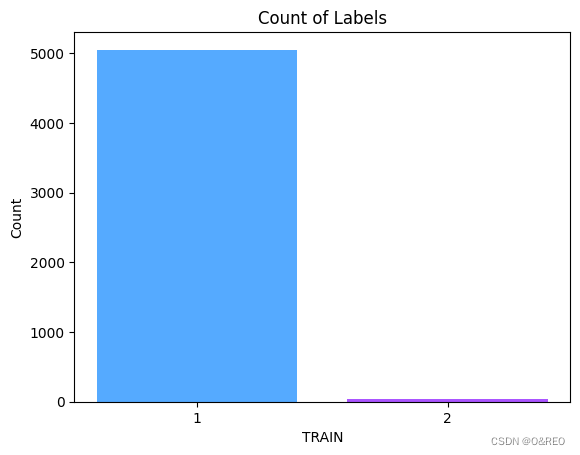
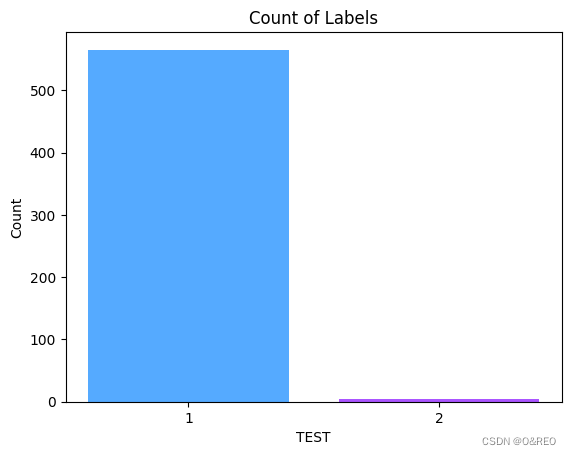
就算我们直接蒙1准确率就接近99%

因此我们需要通过分类报告（其中包含精确率、召回率和F1分数等指标）和混淆矩阵进行进一步的评估。这两个工具才是分类不平衡数据集的真正有效指标。

from sklearn.metrics import classification_report # 分类报告 
from sklearn.metrics import confusion_matrix # 混淆矩阵 
y_prob=model.predict(X_test) # 对测试集进行预测 
y_pred=np.where(y_prob > 0.5, 1, 0) #将概率值转换成真值
print(y_pred)
cm=confusion_matrix(y_pred, y_test) 
print('Confusion matrix:\n', cm, '\n') 
print(classification_report(y_pred, y_test))
plt.title("CNN+RNN Confusion Matrix") # 标题
sns.heatmap(cm, annot=True, cmap="cool", fmt="d", cbar=False) # 热力图设定 
plt.show() # 显示混淆矩阵

 

 

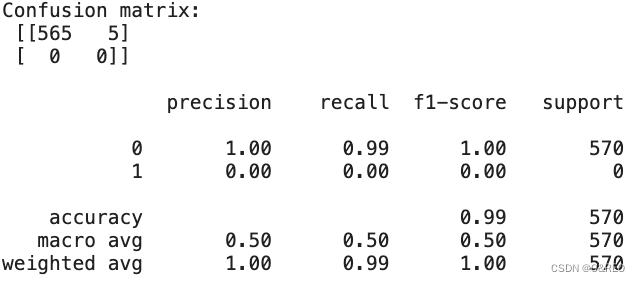
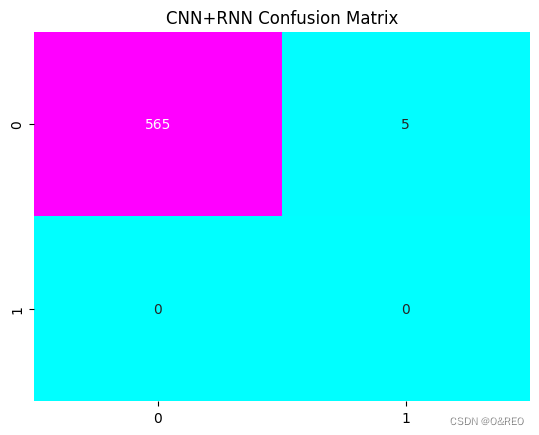
模型也选择了不作为的手段，一个1都没预测

print(y_prob)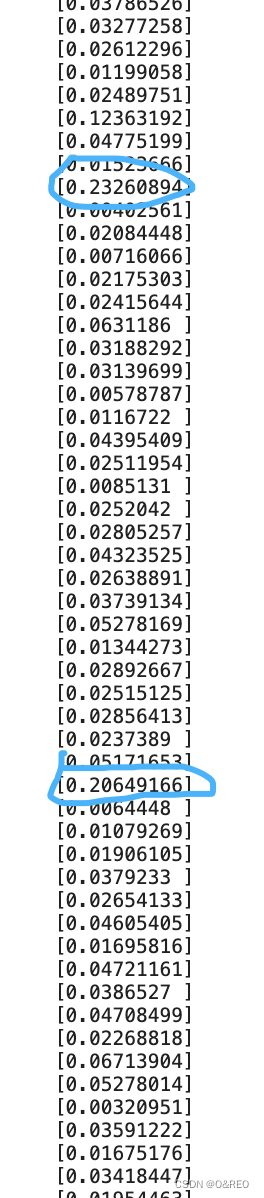

机器学习得到的概率值告诉我们，尽管因为训练集中真值为1的数据过少，导致所有恒星普遍呈现低概率，但是每个恒星的具体概率值不同。仔细观察上面输出的这几行数据，在大多数恒星拥有行星的概率值小于0.1的情况下，其中一些行所显示的约0.2的概率值显著大于其他结果，这个“相对较大”的概率值可能就为我们指向一个有行星的星球。

而当我们将

y_pred=np.where(y_prob > 0.5, 1, 0) #将概率值转换成真值

改为

y_pred=np.where(y_prob > 0.1, 1, 0) #将概率值转换成真值 

 

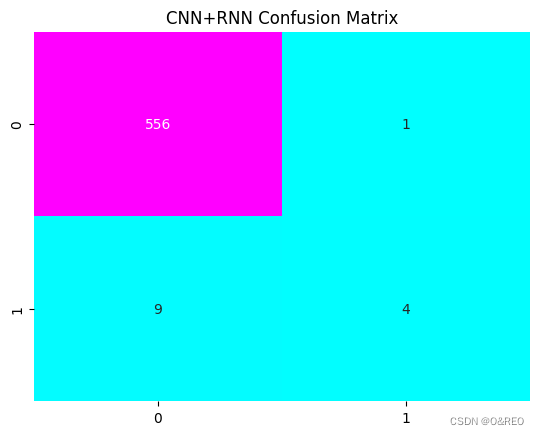
5个有行星星球中成功预测出4个