数据结构 -- 双向链表

谁说我没有死过? 出生以前, 太阳已无数次起落. 悠久的时光被悠久的虚无吞没, 又以我生日的名义卷土重来. --史铁生

---

正文开始

1. 前言

双向链表是一种常见的数据结构，它与单向链表相比，在存储元素的同时还记录了元素的前驱节点。双向链表可以实现双向遍历，不仅可以从头到尾遍历元素，还可以从尾到头遍历。这种特性使得双向链表在某些场景下更加方便和高效。

在双向链表中，每个节点都有两个指针，一个指向前驱节点，一个指向后继节点。这样，我们可以通过前驱指针和后继指针，方便地进行插入、删除、查找等操作。

在接下来的文章中，我们将详细讨论双向链表的实现和常见操作。我们将逐步介绍双向链表的构造、插入、删除、查找等操作，并给出相应的代码示例。通过学习和理解这些操作，我们可以更好地理解和应用双向链表，提升自己的编程能力。让我们开始吧！

更多知识点击: 酷酷学!!!
更多精彩 不要忘了关注哟~~

---

2. 双向链表的结构

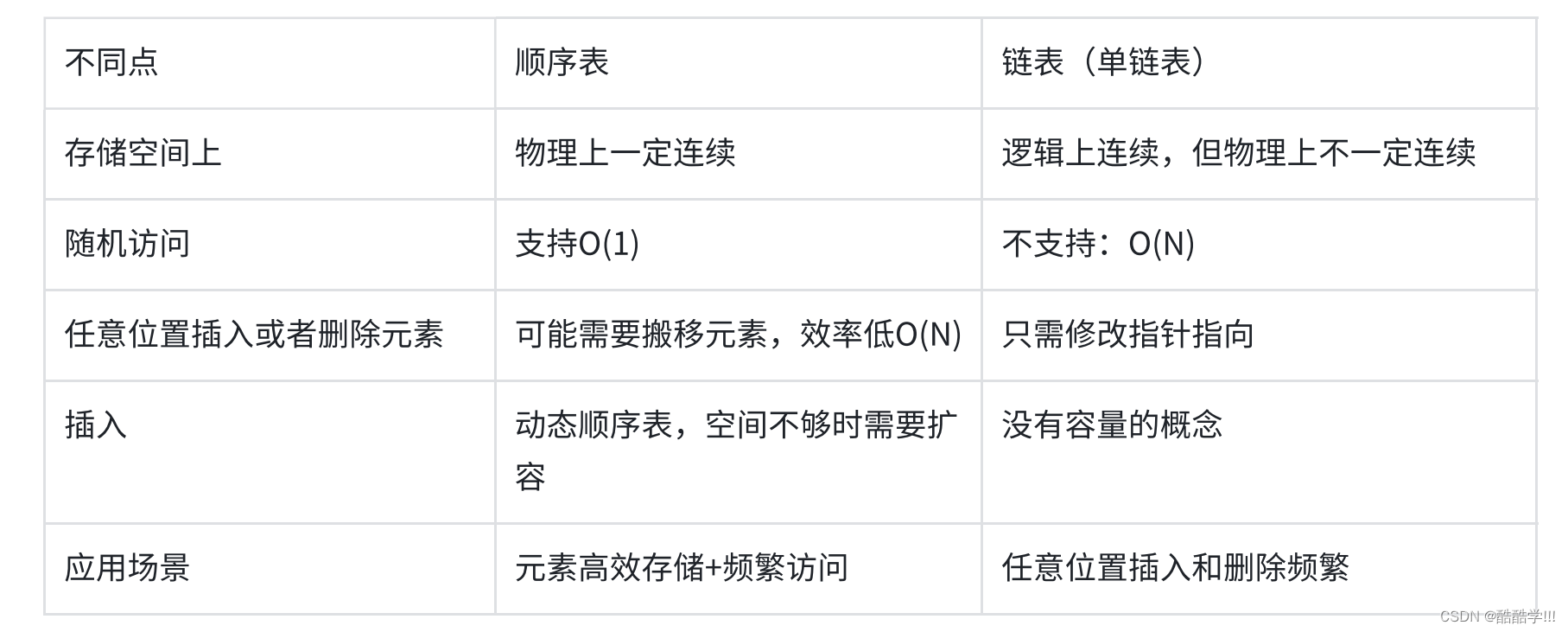
双向链表与顺序表的区别:

注意：

这里的“带头”跟前面我们说的“头节点”是两个概念，实际前面的在单链表阶段称呼不严谨，但是为了更好的理解就直接称为单链表的头节点。带头链表里的头节点，实际为“哨兵位”，哨兵位节点不存储任何有效元素，只是站在这里“放哨的”.

“哨兵位”存在的意义：

遍历循环链表避免死循环。

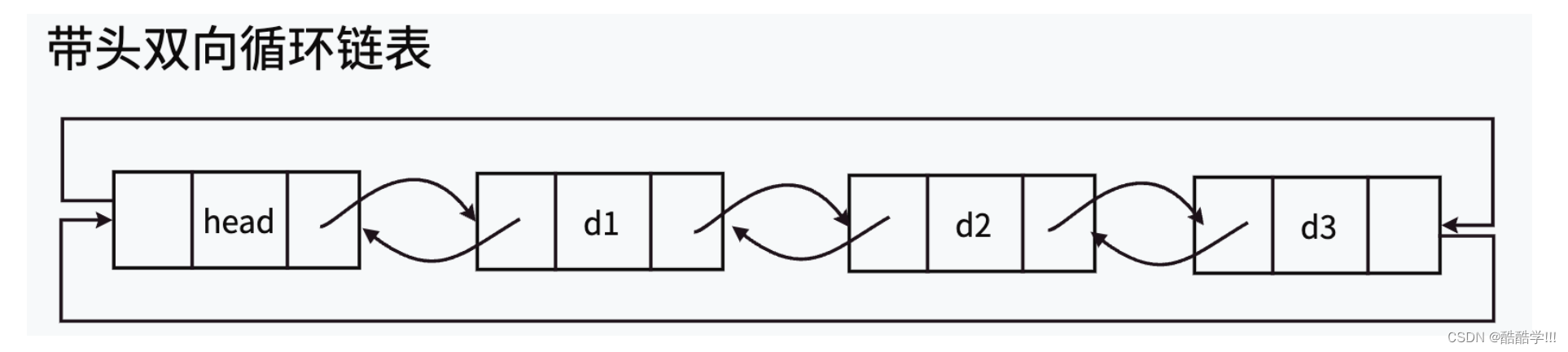
链表的分类可以分为八种, 但最常见的无非两种:

单链表和双向带头循环链表

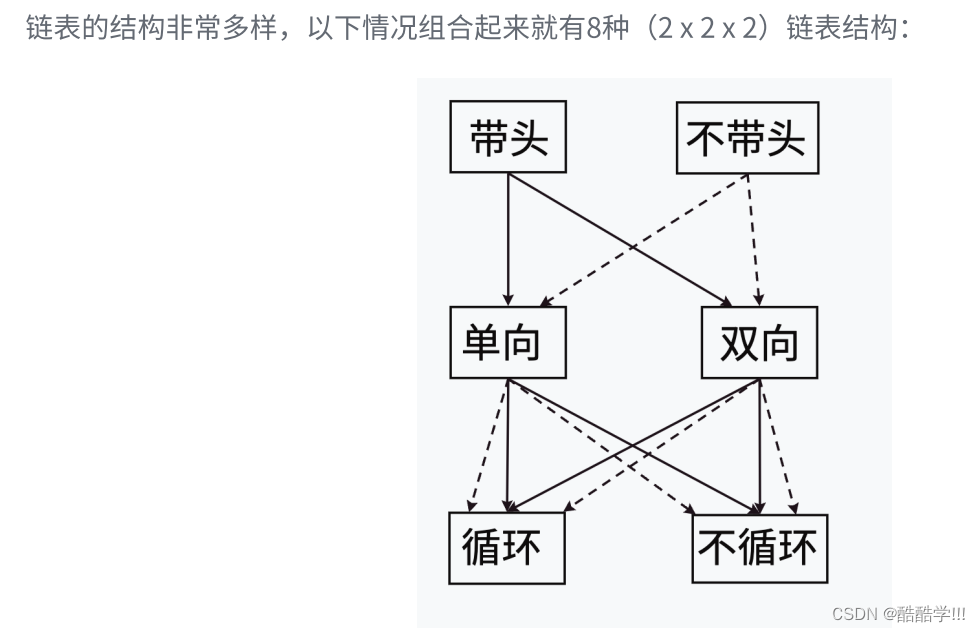
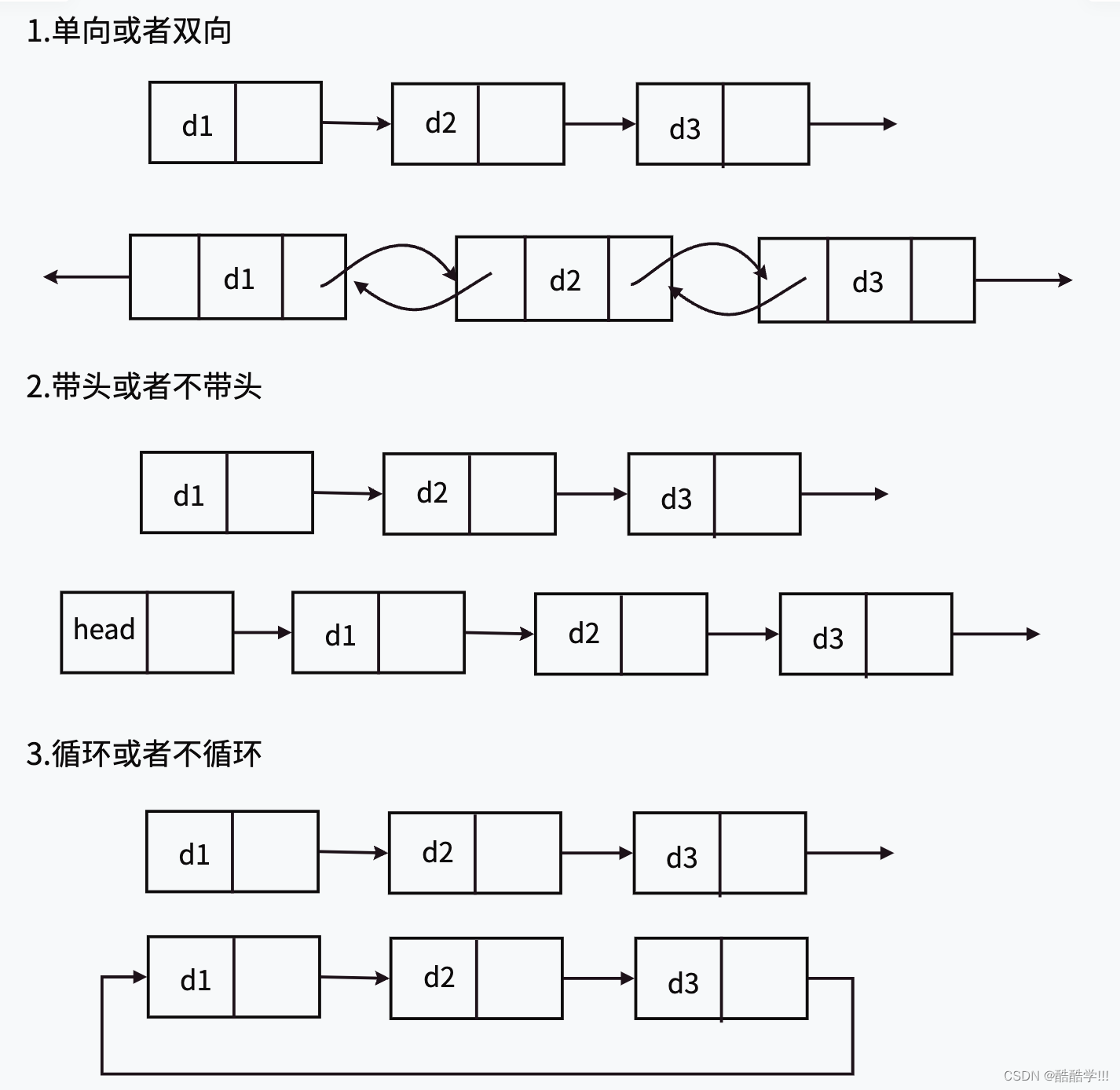
1. 无头单向非循环链表：结构简单，⼀般不会单独⽤来存数据。实际中更多是作为其他数据结构的⼦结构，如哈希桶、图的邻接表等等。另外这种结构在笔试⾯试中出现很多。
2. 带头双向循环链表：结构最复杂，⼀般⽤在单独存储数据。实际中使⽤的链表数据结构，都是带头双向循环链表。另外这个结构虽然结构复杂，但是使⽤代码实现以后会发现结构会带来很多优势，实现反⽽简单了，下面我们就来实现带头双向循环链表.

---

3. 双向链表的实现

第一步:
在头文件中定义和声明需要使用的双向链表结构体和函数的声明, 我们分别创建三个文件, LIst.h 文件主要用来进行类型和函数的声明, List.c文件主要进行函数的实现, test.c用来进行测试文件 :

List.h:

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>

typedef int DataType;

typedef struct ListNode
{
	DataType data;
	struct ListNode* next;
	struct ListNode* prev;
}LTNode;

//初始化
void LTInit(LTNode** pphead);
//LTNode* LTInit();

//尾插
void LTpushBack(LTNode* phead,DataType x);

//打印
void LTprint(LTNode* phead);

//头插

void PushFront(LTNode* phead, DataType x);

//尾删
void PopBack(LTNode* phead);
//头删
void PopFront(LTNode* phead);

//查找
LTNode* LTFind(LTNode* phead, DataType x);

//在指定位置之后插入数据
void LTInsert(LTNode* pos, DataType x);
//删除指定位置数据
void Erase(LTNode* pos);

void LTDestory(LTNode* phead);

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

第二步: 进行链表的初始化, 首先一个双向带头循环链表需要有一个哨兵位, 也就是头结点, 并且需要循环 , 所以可以在test.c中创建一个指针指向这个头结点, 也可以使用函数返回一个指针指向这个函数. 如下:

LTNode* LTBuyNode(DataType x)
{
	LTNode* node = (LTNode*)malloc(sizeof(LTNode));
	if (node == NULL)
	{
		perror("malloc fail");
		exit(1);
	}
	node->data = x;
	node->next = node->prev = node;
	return node;
}

void LTInit(LTNode** pphead)
{
	*pphead = LTBuyNode(-1);
}

//或者

LTNode* LTInit()
{
	LTNode* phead = LTBuyNode(-1);
	return phead;
}


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

第三步: 实现链表的其他方法:
尾插:
这里不需要传递二级指针, 因为phead指向的位置只能是哨兵位, 不可以发生改变, 申请新的结点, 为了不影响原链表, 先改变新节点的前驱指针和后继指针, 在改变受影响的结点.让新节点next指向头结点, prev指向头结点的前驱结点, 在改变d3, 最后改变头结点.

如图:

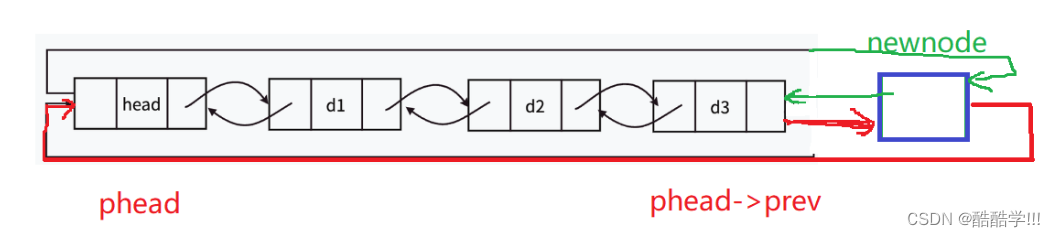
void LTpushBack(LTNode* phead,DataType x)
{
	assert(phead);
	LTNode* newnode = LTBuyNode(x);

	newnode->next = phead;
	newnode->prev = phead->prev;
	phead->prev->next = newnode;//注意这样写不能改变与下一行交换位置
	phead->prev = newnode;
}
1
2
3
4
5
6
7
8
9
10

可以封装一个打印函数来显示我们的链表, 注意结束条件是遍历到phead前停止

void LTprint(LTNode* phead)
{
	assert(phead);
	LTNode* pcur = phead->next;
	while (pcur != phead)
	{
		printf("%d -> ", pcur->data);
		pcur = pcur->next;
	}
	printf("\n");
}
1
2
3
4
5
6
7
8
9
10
11

测试一下:

#define _CRT_SECURE_NO_WARNINGS 1
#include"List.h"


void test01()
{
	LTNode* plist = NULL;
	LTInit(&plist);
	LTpushBack(plist,100);
	LTprint(plist);


}

int main()
{	
	test01();
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

运行结果:

头插:
将新节点插入到头结点之前是尾插, 插入到头结点之后即尾插, 同样先改变新结点, 在改变受到影响的结点.

画图:

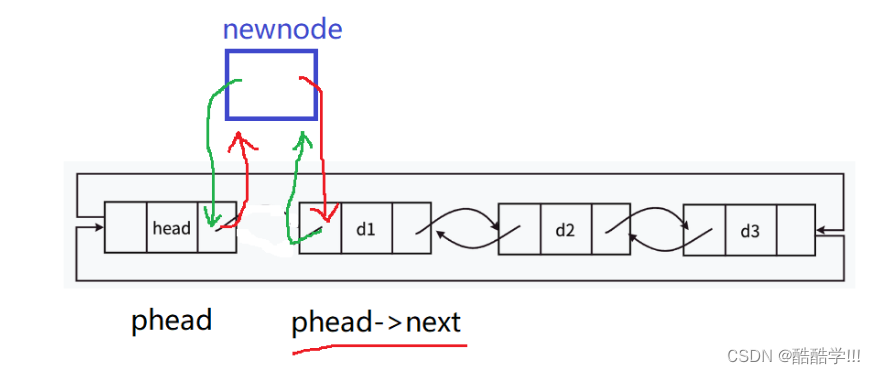
void PushFront(LTNode* phead, DataType x)
{
	assert(phead);

	LTNode* newnode = LTBuyNode(x);

	newnode->next = phead->next;
	newnode->prev = phead;
	phead->next->prev = newnode;//这样写也不能和下一行交换位置
	phead->next = newnode;
}
1
2
3
4
5
6
7
8
9
10
11

尾删:
为了方便理解, 以及减少代码复杂性, 我们先将要删除的结点保存在del中, 然后将del的前一个结点指向del的下一个结点, 也即头结点, 并且改变头结点的前一个结点指向del的前一个结点

画图:

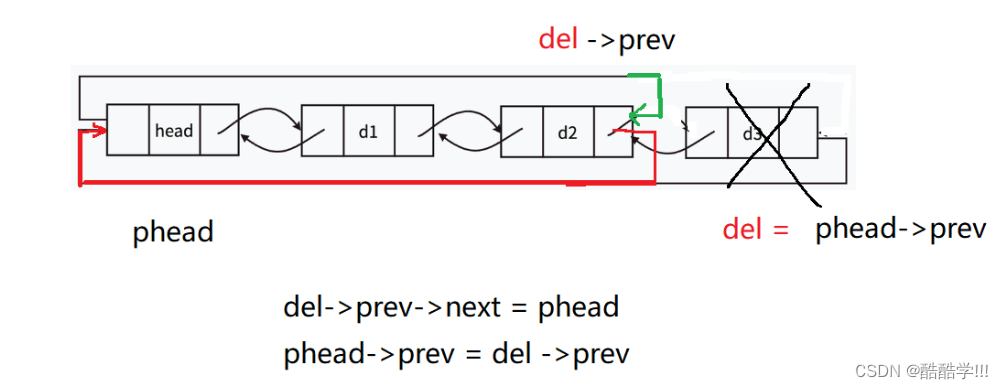
void PopBack(LTNode* phead)
{
	assert(phead && phead->next != phead);

	LTNode* del = phead->prev;
	del->prev->next = phead;
	phead->prev = del->prev;
	free(del);
	del = NULL;
}

1
2
3
4
5
6
7
8
9
10
11

头删:
头删就是删除头结点的下一个结点, 先将要删除的结点保存到del中, 改变del的下一个结点的前驱结点指向头结点, 并且改变头结点的下一个结点指向del的下一个结点.

画图:

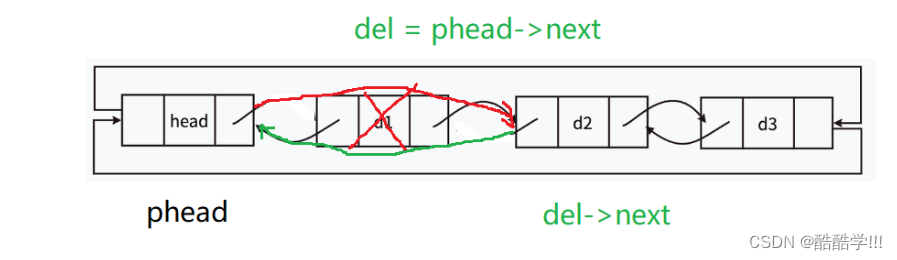
void PopFront(LTNode* phead)
{
	assert(phead && phead->next != phead);

	LTNode* del = phead->next;

	phead->next = del->next;
	del->next->prev = phead;

	free(del);
	del = NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12

查找:
下面将实现一个查找函数, 以便于我们找到指定位置, 用作后续的指定位置的插入和删除, 其实和打印函数的思想基本一致, 只是遍历的途中需要与x值进行对比, 找到了就返回该地址.

LTNode* LTFind(LTNode* phead, DataType x)
{
	assert(phead);
	LTNode* pcur = phead->next;
	while (pcur != phead)
	{
		if (pcur->data == x)
		{
			return pcur;
		}
		pcur = pcur->next;
	}
	return NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

在指定位置的插入:
此时我们并不需要头结点了, 根据pos的指针域就可以找到要插入的位置, 并且申请新节点, 改变指针域就可以了,代码也非常简单, 逻辑也非常简单

画图:

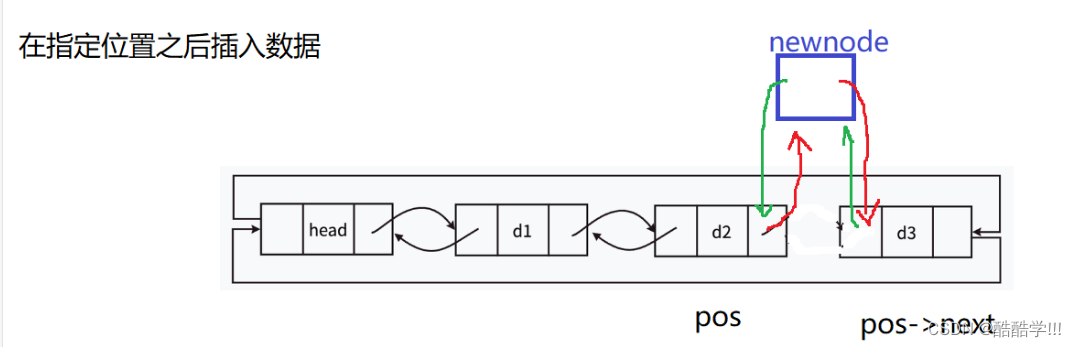
void LTInsert(LTNode* pos, DataType x)
{
	assert(pos);

	LTNode* newnode = LTBuyNode(x);

	newnode->next = pos->next;
	newnode->prev = pos;

	pos->next->prev = newnode;
	pos->next = newnode;
}
1
2
3
4
5
6
7
8
9
10
11
12

删除指定位置:
和前面的删除思想基本一致, 改变受到影响的结点之后, 销毁此节点.

画图:

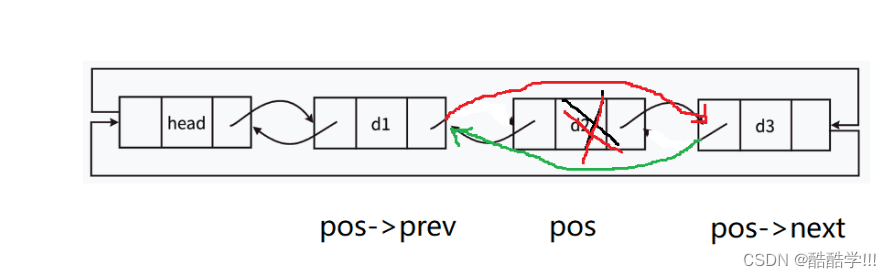
void Erase(LTNode* pos)
{
	assert(pos);

	pos->next->prev = pos->prev;
	pos->prev->next = pos->next;

	free(pos);
	pos = NULL;
}
1
2
3
4
5
6
7
8
9
10

最后一步: 销毁结点, 既然动态开辟了内存, 我们就需要手动释放, 因为我们这传递的是一级指针, 所以形参不会影响实参, 在测试代码中需要再次将phead的值置为NULL, 但是我们为了代码的一致性, 传递了一级指针, 遍历链表, 保存下一个结点, 以此销毁, 最后销毁头结点.

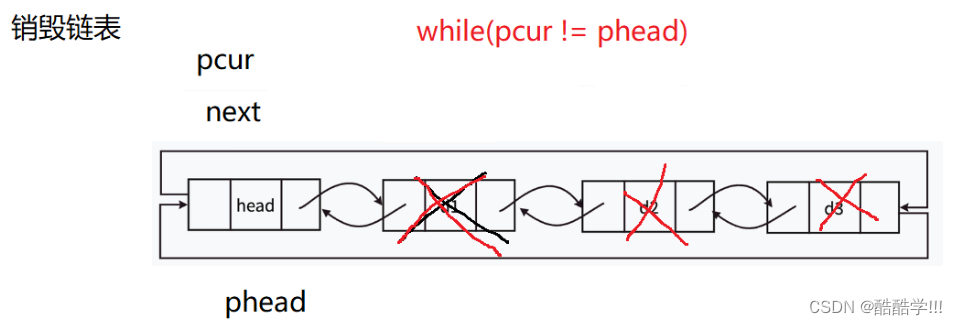
void LTDestory(LTNode* phead)
{
	assert(phead);

	LTNode* pcur = phead->next;
	while (pcur != phead)
	{
		LTNode* next = pcur->next;
		free(pcur);
		pcur = next;
	}
	free(phead);
	phead = NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

---

4. 完整代码

List.c

#define _CRT_SECURE_NO_WARNINGS 1

#include"List.h"

LTNode* LTBuyNode(DataType x)
{
	LTNode* node = (LTNode*)malloc(sizeof(LTNode));
	if (node == NULL)
	{
		perror("malloc fail");
		exit(1);
	}
	node->data = x;
	node->next = node->prev = node;
	return node;
}

void LTInit(LTNode** pphead)
{
	*pphead = LTBuyNode(-1);
}

void LTpushBack(LTNode* phead,DataType x)
{
	assert(phead);
	LTNode* newnode = LTBuyNode(x);

	newnode->next = phead;
	newnode->prev = phead->prev;
	phead->prev->next = newnode;
	phead->prev = newnode;
}

void LTprint(LTNode* phead)
{
	assert(phead);
	LTNode* pcur = phead->next;
	while (pcur != phead)
	{
		printf("%d -> ", pcur->data);
		pcur = pcur->next;
	}
	printf("\n");
}

void PushFront(LTNode* phead, DataType x)
{
	assert(phead);

	LTNode* newnode = LTBuyNode(x);

	newnode->next = phead->next;
	newnode->prev = phead;
	phead->next->prev = newnode;
	phead->next = newnode;
}

void PopBack(LTNode* phead)
{
	assert(phead && phead->next != phead);

	LTNode* del = phead->prev;
	del->prev->next = phead;
	phead->prev = del->prev;
	free(del);
	del = NULL;
}

void PopFront(LTNode* phead)
{
	assert(phead && phead->next != phead);

	LTNode* del = phead->next;

	phead->next = del->next;
	del->next->prev = phead;

	free(del);
	del = NULL;
}

LTNode* LTFind(LTNode* phead, DataType x)
{
	assert(phead);
	LTNode* pcur = phead->next;
	while (pcur != phead)
	{
		if (pcur->data == x)
		{
			return pcur;
		}
		pcur = pcur->next;
	}
	return NULL;
}
void LTInsert(LTNode* pos, DataType x)
{
	assert(pos);

	LTNode* newnode = LTBuyNode(x);

	newnode->next = pos->next;
	newnode->prev = pos;

	pos->next->prev = newnode;
	pos->next = newnode;
}

void Erase(LTNode* pos)
{
	assert(pos);

	pos->next->prev = pos->prev;
	pos->prev->next = pos->next;

	free(pos);
	pos = NULL;
}

void LTDestory(LTNode* phead)
{
	assert(phead);

	LTNode* pcur = phead->next;
	while (pcur != phead)
	{
		LTNode* next = pcur->next;
		free(pcur);
		pcur = next;
	}
	free(phead);
	phead = NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133

List.h

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>

typedef int DataType;

typedef struct ListNode
{
	DataType data;
	struct ListNode* next;
	struct ListNode* prev;
}LTNode;

//初始化
void LTInit(LTNode** pphead);

//尾插
void LTpushBack(LTNode* phead,DataType x);

//打印
void LTprint(LTNode* phead);

//头插

void PushFront(LTNode* phead, DataType x);

//尾删
void PopBack(LTNode* phead);
//头删
void PopFront(LTNode* phead);

//查找
LTNode* LTFind(LTNode* phead, DataType x);

//在指定位置之后插入数据
void LTInsert(LTNode* pos, DataType x);
//删除指定位置数据
void Erase(LTNode* pos);

void LTDestory(LTNode* phead);

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

test.c

#define _CRT_SECURE_NO_WARNINGS 1
#include"List.h"


void test01()
{
	LTNode* plist = NULL;
	LTInit(&plist);
	LTpushBack(plist,100);
//	PushFront(plist, 200);
//	PushFront(plist, 300);
//
//	LTNode* find = LTFind(plist, 100);
	PopBack(plist);
//	LTInsert(find, 888);
//
//	Erase(find);
//	find = NULL;

	//LTDestory(plist);
	//plist = NULL;
	//plist = NULL;
	LTprint(plist);


}

int main()
{	
	test01();
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

---

5. 总结

是不是发现双向链表的实现更加容易了呢, 这是因为我们不需要像单链表一样每次都遍历结点, 总的来说，双向链表是一种功能强大的数据结构，拥有插入、删除和反向遍历等额外功能。然而，它也增加了额外的复杂性和内存开销。在选择数据结构时，需要根据具体的场景和需求来权衡使用双向链表的优缺点。

---

完 , 感谢铁子们的支持 别忘了 关注+点赞 ~~~