- 1myCobot pro 机械臂(6)逆向运动学_机械臂逆运动学
- 2Flink CDC 整库 / 多表同步至 Kafka 方案(附源码)_cdckafka
- 3Your branch and 'origin/master' have diverged, and have # and # different commits each, respectively
- 4python实现Android实时投屏操控_scrcpy投屏python
- 5职场生存法则和处世之道_职场处事之道
- 6《从零开始学python+自然语言处理100题》——给自己的记录_自然语言处理100练
- 7【深度学习图像识别课程】keras实现CNN系列:(7)迁移学习的原理和应用_机器学习、迁移学习和cnn
- 8windows版redis_redis windows
- 9分布式学习-总结
- 10图像分割实战-系列教程2:Unet系列算法(Unet、Unet++、Unet+++、网络架构、损失计算方法)
梯度,hesse阵与Jacobi矩阵
赞
踩
分清楚三个量的含义和计算方法。
梯度
表征的是一个列向量,是相对于某个方向而言的,但是某个方向上可能有多个变量,所以梯度不是简单的直接求偏导,并且说了,它是一个列向量,所以,
我们设
f
:
F
f:F
f:F是
R
n
R^n
Rn->
R
R
R的一阶连续可微函数,则
f
f
f在
x
x
x处的一阶偏导数:
∇
\nabla
∇
f
(
x
)
f(x)
f(x)=(
∂
f
(
x
)
∂
x
1
\frac{\partial f(x)}{\partial x_1}
∂x1∂f(x),
∂
f
(
x
)
∂
x
1
\frac{\partial f(x)}{\partial x_1}
∂x1∂f(x),
⋯
\cdots
⋯,
∂
f
(
x
)
∂
x
n
\frac{\partial f(x)}{\partial x_n}
∂xn∂f(x))
T
^T
T
即:
∇
f
(
x
)
=
(
∂
f
(
x
)
∂
x
1
∂
f
(
x
)
∂
x
2
⋮
∂
f
(
x
)
∂
x
n
)
\nabla{f(x)}=\left(
所以说是一个
R
n
−
>
R
R_n->R
Rn−>R的变换
hesse阵
在梯度的基础上就是二阶偏导就是hesse阵,注意由于是二阶偏导,所以不止是平方,还有混合偏导数的存在。
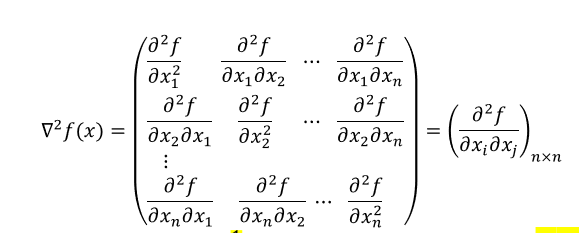
∇
2
f
(
x
)
\nabla^2{f(x)}
∇2f(x)=(
∂
2
f
∂
x
i
∂
x
j
)
n
×
n
\frac{\partial^2{f}}{\partial{x_i}\partial{x_j}})_{n\times n}
∂xi∂xj∂2f)n×n
∇
2
f
(
x
)
=
(
∂
2
f
∂
x
1
2
∂
2
f
∂
x
1
∂
x
2
⋯
∂
2
f
∂
x
1
∂
x
n
∂
2
f
∂
x
2
∂
x
1
∂
2
f
∂
x
2
2
⋯
∂
2
f
∂
x
2
∂
x
n
⋮
∂
2
f
∂
x
n
∂
x
1
∂
2
f
∂
x
n
∂
x
2
⋯
∂
2
f
∂
x
n
2
)
\nabla^2f(x)=\left(
每一行都已
x
i
x_i
xi开始,然后求二阶继续从
x
i
x_i
xi到
x
n
x_n
xn求出
雅可比
其实是一种维度拓宽的梯度的表示方法,也就是
f
f
f是
F
⊆
R
n
→
R
m
F\subseteq{R^n}\rightarrow{R^m}
F⊆Rn→Rm,
x
x
x在F上连续可微,则一阶导数为:
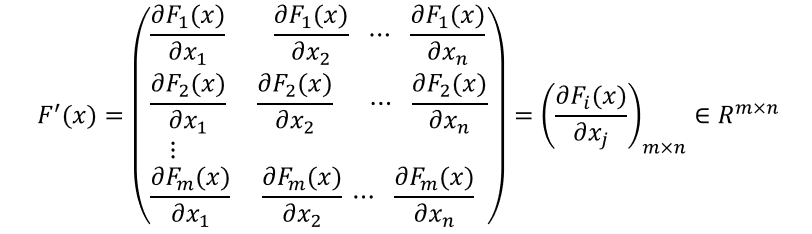
F
′
(
x
)
=
(
∂
F
i
(
x
)
∂
x
j
)
m
×
n
∈
R
m
×
n
F'(x)=(\frac{\partial{F_i(x)}}{\partial{x_j}})_{m\times n}\in{R^{m\times n}}
F′(x)=(∂xj∂Fi(x))m×n∈Rm×n
也就是说,向量值函数的导数就是雅可比矩阵,向量中的每一项分别求梯度再组合起来。
比如:对于
f
:
R
n
→
R
f:R^n \rightarrow R
f:Rn→R
我们可以和梯度以及hesse阵联系起来看Jacobi矩阵,
H
(
x
)
=
J
(
∇
f
(
x
)
)
H(x)=J(\nabla f(x))
H(x)=J(∇f(x))
H
(
x
)
=
∇
2
f
(
x
)
H(x)=\nabla^2f(x)
H(x)=∇2f(x)
梯度的Jacobi矩阵就是hesse阵。
举个例子说明一下:
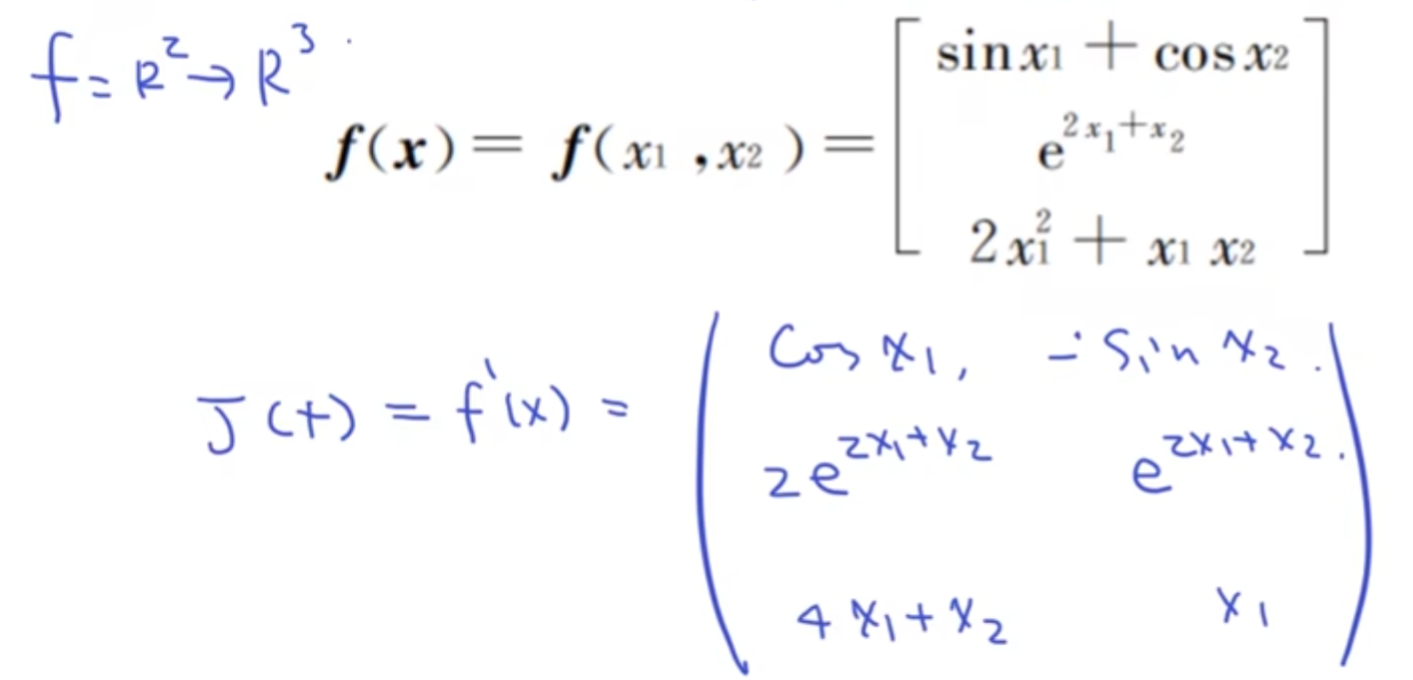
以上用到的markdown语法
分数
x
y
\frac{x}{y}
yx \frac{x}{y}
偏导数
∂
f
(
x
)
\partial{f(x)}
∂f(x) \partial{f(x)}
梯度
∇
f
(
x
)
\nabla{f(x)}
∇f(x) \nabla{f(x)}
表示x_1^2的:
x
i
j
x_i^j
xij
×:\times
vdots
cdots
\leftarrow
\rightarrow
\in 属于
⊆
\subseteq
⊆ 包含 \subseteq


