- 1【初阶数据结构】单链表之环形链表
- 2无法访问hadoop yarn8088端口的解决方法_hadoop集群访问不了yarn网页
- 3k8s中job与cronjob使用详解_cronjob配置
- 4关于prompt中的一些命令_prompt指令合集
- 5android.mk 条件编译,android openSSL 的苦逼历程
- 6【爬虫】Python+Scrapy+Selenium简单爬取淘宝天猫商品信息及评论_用selenium爬华为商城商品评论
- 7git reset简介_git reset 所有unmerge
- 8Android之SQLite数据库及SQLiteStudio工具的使用,全网最新_androidstudio的sqlite创建工具类
- 9HashMap1.8_lohead lotail hihead hitail
- 10Google Chrome 设备工具栏原理
什么是布隆过滤器
赞
踩
什么是布隆过滤器
布隆过滤器能够实现使用较少的空间来判断一个指定的元素是否包含在一个集合中
布隆过滤器并不保存这些数据,所以只能判断是否存在,而并不能取出该元素
布隆过滤器常见使用场景
1. idea中编写代码,一个单词是否包含在正确拼写的词库中(拼写不正确划绿线的提示)
2. 公安系统,根据身份证号\人脸信息,判断该人是否在追逃名单中
3. 爬虫检查一个网址是否被爬取过
.....
宗旨:凡是判断一个元素是否在一个集合中的操作,都可以使用它
为什么使用布隆过滤器
常规的检查一个元素是否在一个集合中的思路是遍历集合,判断元素是否相等
这样的查询效率非常低下
要保证快速确定一个元素是否在一个集合中,我们可以使用HashMap
因为HashMap内部的散列机制,保证更快更高效的找到元素
所以当数据量较小时,用HashMap或HashSet保存对象然后使用它来判定元素是否存在是不错的选择
但是如果数据量太大,每个元素都要生成哈希值来保存,我们也要依靠哈希值来判定是否存在,一般情况下,我们为了保证尽量少的哈希值冲突需要8字节哈希值做保存
long取值范围:-9223372036854775808-----9223372036854775807
5亿条数据 每条8字节计算后结果为需要3.72G内存,随着内存数增长,这个数字可能更大
所以Hash散列或类似算法可以保证高效判断元素是否存在,但是消耗内存较多
所以我们使用布隆过滤器实现,高效判断是否存在的同时,还能节省内存的效果
但是布隆过滤器的算法天生会有误判情况,需要能够容忍,才能使用
布隆过滤器原理
- 巴顿.布隆于⼀九七零年提出
- ⼀个很长的⼆进制向量(位数组)
- ⼀系列随机函数 (哈希)
- 空间效率和查询效率⾼
- 有⼀定的误判率(哈希表是精确匹配)

如果我们向布隆过滤器中保存一个单词
semlinker
我们使用3个hash算法,找到布隆过滤器的位置
算法1:semlinker--> 2
算法2:semlinker--> 4
算法3:semlinker--> 6
会在布隆过滤器中产生如下影响
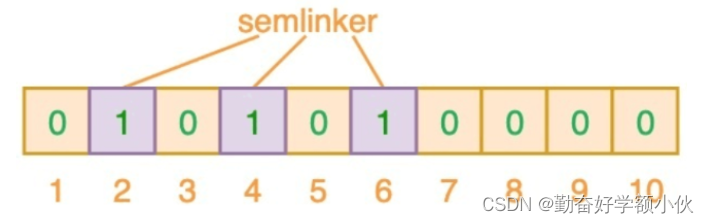
查询"Good"在不在布隆过滤器中
算法1:Good-->7
算法2:Good-->3
算法3:Good-->6
我们判断Good单词生成的3,6,7三个位置,只要有一个位置是0
就表示当前集合中没有Good这个单词
一个布隆过滤器不可能存一个单词,一般布隆过滤器都是保存大量数据的
如果有新的元素保存在布隆过滤器中
kakuqo
算法1:kakuqo-->3
算法2:kakuqo-->4
算法3:kakuqo-->7

新的单词生成3,4,7个位置
那么现在这个布隆过滤器中2,3,4,6,7都是1了
bad
算法1:bad-->2
算法2:bad-->3
算法3:bad-->6
判断布隆过滤器2,3,6都是1,所以布隆过滤器会认为bad是存在于这个集合中的
**误判就是这样产生的**
布隆过滤器误判的效果:
- 布隆过滤器判断不存在的,一定不在集合中
- 布隆过滤器判断存在的,有可能不在集合中
过短的布隆过滤器如果保存了很多的数据,可能造成二进制位置值都是1的情况,一旦发送这种情况,布隆过滤器就会判断任何元素都在当前集合中,布隆过滤器也就失效了
所以我们要给布隆过滤器一个合适的大小才能让它更好的为程序服务
- 优点
空间效率和查询效率⾼,
- 缺点
- 有⼀定误判率即可(在可接受范围内)。
- 删除元素困难(不能将该元素hash算法结果位置修改为0,因为可能会影响其他元素)
- 极端情况下,如果布隆过滤器所有为位置都是1,那么任何元素都会被判断为存在于集合中
设计布隆过滤器
我们在启动布隆过滤器时,需要给它分配一个合理大小的内存
这个大小应该满足
1.内存占用在一个可接受范围
2.不能有太高的误判率(<1%)
内存约节省,误判率越高
内存越大,误判率越低
数学家已经给我们了公式计算误判率

上面是根据误判率计算布隆过滤器长度的公式
n 是已经添加元素的数量;
k 哈希的次数;
m 布隆过滤器的长度(位数的大小)
计算结果就是误判率
如果我们已经确定可接受的误判率,想计算需要多少 布隆过滤器的长度

布隆过滤器计算器
https://hur.st/bloomfilter
windows安装redisbloom布隆过滤器
https://blog.csdn.net/weixin_44770915/article/details/107918770


