2022年电工杯数学建模B题5G网络环境下应急物资配送问题求解全过程论文及程序_数学建模无人机取送货问题

2022年电工杯数学建模

B题 5G网络环境下应急物资配送问题

原题再现：

  一些重特大突发事件往往会造成道路阻断、损坏、封闭等意想不到的情况，对人们的日常生活会造成一定的影响。为了保证人们的正常生活，将应急物资及时准确地配送到位尤为重要。伴随着科技水平的提升及 5G 网络的逐渐普及，无人机的应用越来越广泛，“配送车辆+无人机”的配送模式已经渐渐成为一种新的有效的配送方式。
  “配送车辆+无人机”的配送模式是指：在物资配送过程中，配送车辆对某地点进行配送的同时，无人机也可向周围可行的地点进行配送，并于配送完成后返回配送车辆重新装载物资、更换电池。这种配送模式可以大大提高应急物资的配送效率，也可以解决复杂路况下的物资配送，避免次生灾害对人员的二次伤害。
  在应急物资配送过程中，配送车辆可在某地点释放无人机，再前往其它地点配送。配送车辆可先于无人机到达某地点等待接收无人机，也可比无人机晚到某地点再回收无人机。无人机在一次飞行过程中可对一个地点进行配送，也可根据实际情况对多个地点进行配送。无人机完成一次飞行后可返回配送车辆换装电池，然后再次进行配送。配送车辆和无人机合作完成所有地点应急物资配送任务，返回到出发地点，此时称为完成一次整体配送。
  完成一次整体配送所需要的时间是配送人员主要考虑的因素，按照配送车辆和无人机从出发开始至全部返回到出发地点的时间来计算。在配送过程中，不考虑配送车辆及无人机装卸物资的时间，同时不考虑配送车辆和无人机在各个配送点的停留时间。
  为了尽快完成物资配送任务，请根据附件所给数据解决以下几个问题：
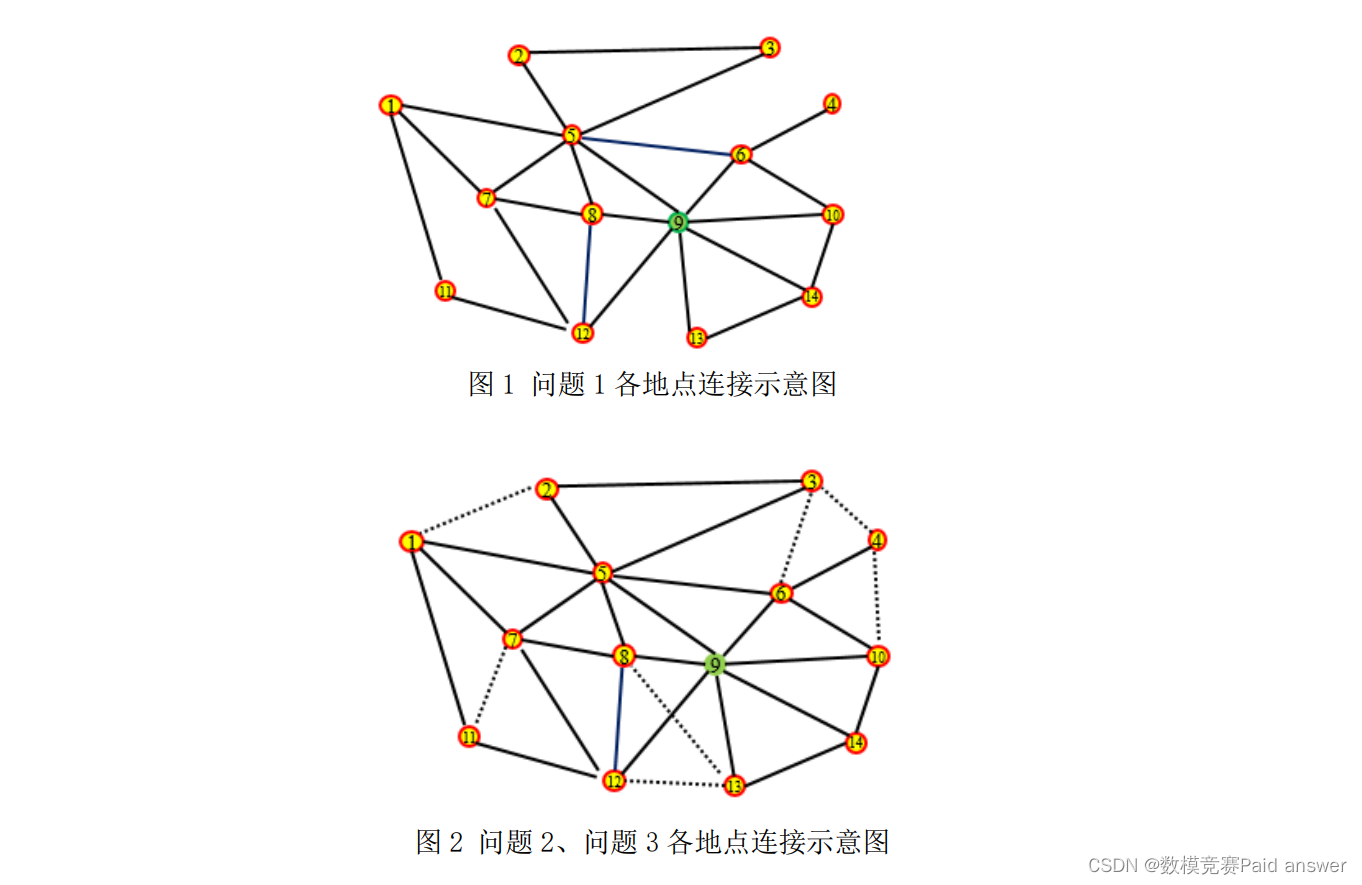
  1.图 1 给出 14 个地点，其中实线代表各地点之间的路线情况。若目前所有应急物资集中在第 9 个地点，配送车辆的最大载重量为 1000 千克，采取配送车辆（无人机不参与）的配送模式。请结合附件 1，建立完成一次整体配送的数学模型，并给出最优方案。
  2.图 2 中实线代表车辆和无人机都可以走的路线，虚线代表只有无人机可以走的路线。应急物资仍然集中在第 9 个地点，配送车辆的最大载重量为 1000 千克，采取“配送车辆+无人机”的配送模式。请结合附件 2，建立完成一次整体配送的数学模型，并给出最优方案。
  3.若问题 2 中的配送车辆的最大载重量为 500 千克，其他条件不变。请结合附件 2，建立完成一次整体配送的数学模型，并给出最优方案。
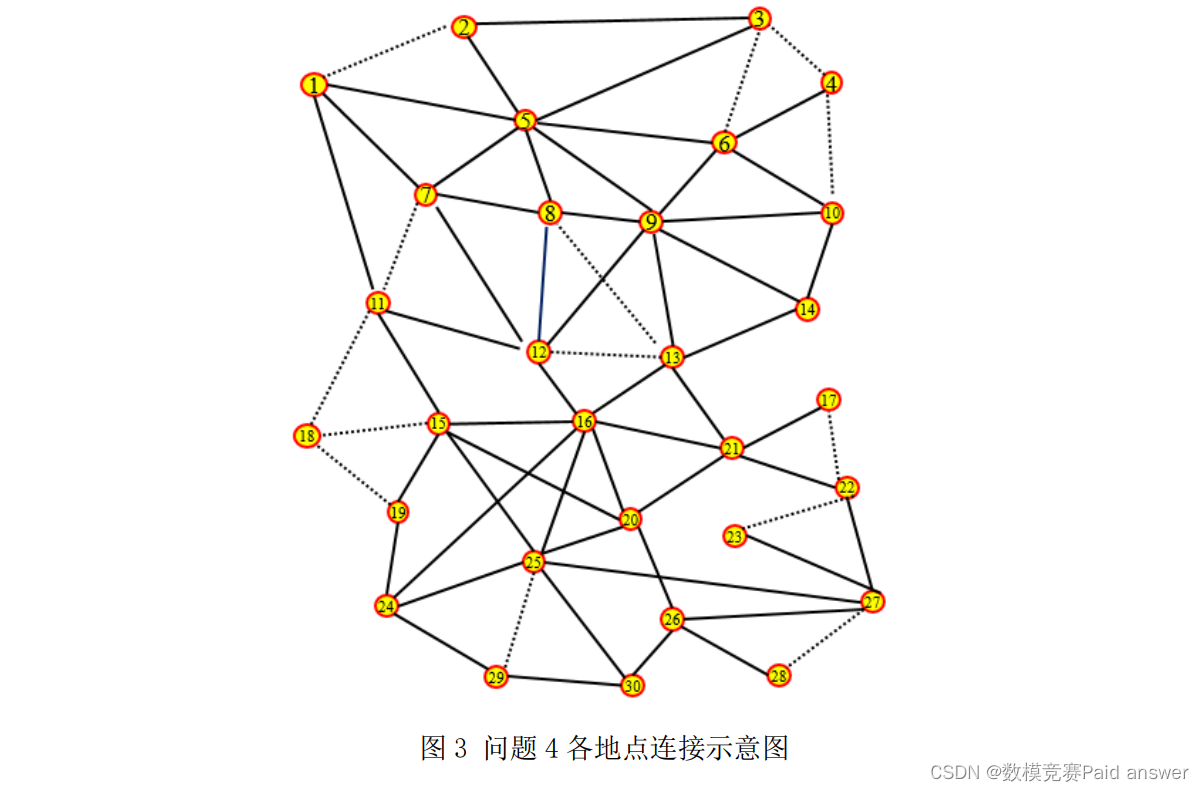
  4.图 3 中有 30 个地点，计划设置两个应急物资集中地点，若配送车辆的最大载重量为 500 千克，采取“配送车辆+无人机”的配送模式。请结合附件 3，建立完成一次整体配送的数学模型，确定两个应急物资集中地点的最佳位置。
  注：
  1.假设应急物资配送前 5G 网络能够覆盖整个配送区域。
  2.忽略无人机自身重量的影响，无人机的最大载重量为 50 千克；配送车辆行驶平均速度为 50 公里/小时，无人机飞行平均速度为 75 公里/小时；无人机单次最长飞行时间为 70 分钟。
  3.每个应急物资集中地点限一辆配送车辆，只能携带一架无人机。
  4.在论文附录中提供所有数学模型的可运行程序。

整体求解过程概述(摘要)

  随着无人机的应用越来越广泛，配送车辆 + 无人机的配送模式已经渐渐成为一种新型有效的配送方式。本文主要研究在这种配送方式下的应急配送问题，建立了基于混合蚁群算法的 VRPD问题模型，利用蚁群算法，迭代局部搜索算法，聚类分析等方法进行求解。
  对于问题一只有配送车辆配送这一模式，建立 VRP 问题，首先通过 floyd 算法验证各地点间的最短距离即为直线距离，将问题转换为最佳 H 圈问题；之后采用蚁群算法对这问题进行迭代求解，得到配送车辆一次整体配送的最短路径和为 582（公里），一次整体配送的最短时间为 11.64（小时），并且发现收敛时迭代次数基本小于 10 次。
  对于问题二，在问题一的基础上新增无人机配送的模式，首先对 14 个地点进行聚类，发现它们属于同一个类；其次在类中进行分区，考虑到无人机的飞行约束，利用椭圆的几何性质最终分为 5 个飞行区；之后采用迭代局部搜索的方式对各飞行区中的点进行重分配，找到最优的配送路线；最后，采用蚁群算法对路线进行迭代求解，得到一次整体配送的最短时间为 6.32（小时），相较问题一时间缩短了近 50%。
  对于问题三，在问题二的基础上增加了配送车的容量限制，这使得配送车不得不中途回到物资集中点装载货物后再次送货，这会使得车辆在路径图中需要经历两个回路。我们在问题二求出的最优路径上将无人机配送的物资需求点记录到配送车释放无人机的节点上，这将我们的问题从带容量约束的无人机 + 配送车问题转化为带容量的车辆路径问题。利用蚁群算法求解该问题，得到最短配送时间为 6.8 小时，这个时间只比单一回路的问题二增加了 7.6%。
  对于问题四，要求我们在 30 个应急物资需求点中选取两个作为物资集中地点，对于这类选址问题，我们采用多种聚类方案将这 30 个点聚为两类，以每个类的中心点作为物资集中点，利用问题二三设计的算法计算各种聚类方式下的物资配送时间，最终我们以质心为条件进行 k-meams 聚类，得到使得物资中心配送时间最短的两个地点为第 8 与第 23 个地点，即为应急物资集中点的最佳地点。
  最后对本文所建立的模型进行了讨论和分析，总结其优缺点，综合评价模型。

模型假设：

  1. 从配送中心出发的车辆必须返回配送中心；
  2. 所有距离都用欧式距离来表示；
  3. 卡车和无人机均以题目给出的数据匀速行驶，且其行驶速度不随其载重改变；
  4. 5G 网络已经覆盖我们需要配送的整个区域；
  5. 不考虑配送车辆和无人机装载和卸货的时间；
  6. 不考虑无人机在配送车上更换电池的时间；
  7. 每个配送点有且只有一辆车或一个无人机进行配送服务；
  8. 假设题目给出的所有路径都是双向路径。

问题分析：

  问题一的分析
  问题一结合附件 1 给出了各地点之间的距离和所需物资量，通过附件 1 我们可以很明显算出总物资需求量为 762 千克，远远小于配送车辆的最大载重量 1000 千克，所以我们只需要考虑求解配送车辆在图 1 中经历一次回路的最短路径，即最佳推销员回路问题，也即 NP-完全问题。考虑到最佳推销员回路问题的求解方法，考虑将其转换为最佳 H 圈问题，利用两者在加权图中的权值是相同的这一定理来求解。通过 Floyd 算法证明各地点之间的直线距离即为它们的最短距离，则说明该问题可以转换为最佳 H 圈问题，其次根据得到的各地点距离形成的完备加权图，最终将在加权图中寻求最佳推销员回路问题转化为在一个完备加权图中寻求最佳 H 圈问题，也称为 TSP 问题。本题中车辆路径的规划问题（VSP 问题），作为 TSP 问题的一个推广可以通过蚁群算法进行对该 VRP 问题的求解，得到从物资集中的第九个地点开始配送直到最后回到该地点的路线图以及一次整体配送的最短路径长度。
  问题二的分析
  问题二在问题一的基础上，增加了无人机配送物资的形式，所以我们的模型求解是在问题一的基础上进行优化改进的。首先我们对图二中的 14 个地点进行聚类，找到超过无人机载重需求或者不在无人机配送范围内的地点，这些地点只能由配送车辆进行配送，所以作为停靠点，针对该题我们采用并查集进行分类；分类后对其中的地点进行分区，通过对无人机的可达地点进行分析，找到在以两个停靠点为焦点形成的椭圆范围内无人机可以配送的范围，作为一个可飞行区，以此为基础对分好的类进行分割，找到所有的可飞行区；之后对各可飞行区中的地点节点进行重分配，找到最合适的无人机和配送车辆要配送的地点。我们通过采用迭代局部搜索的启发式搜索算法找到最优解；最后将以上得到的所有路径进行连接，连接的过程与 TSP 问题较为相似，因此我们仍采用问题一中的蚁群算法进行求解得出完整的连接路径，实现一次整体配送，此时得到的即为时间最短路径。
  问题三的分析
  问题三在问题二的基础上增加了对配送车的容量限制，这使得配送车必须在送货途中回到 9号节点进行补货才能把物资运送完，及由原来的寻找一条最短回路的问题转变为需要两条回路访问图中所有的节点。考虑在问题二求得的最短路径上进行优化，由于将各个飞行区的配送需求压缩到无人机起飞的停靠点上，这样就将问题简化为带容量约束的 VRP 问题，再使用蚁群算法寻找带容量约束的 VRP 问题的最优路径。
  问题四的分析
  我们首先对第四问的图以欧式距离为度量，进行 K-means 聚类，在 30 个应急物资需求点中选取两个作为物资集中地点，对于这类选址问题，我们采用多种聚类方案将这 30 个点聚为两类，以每个类的中心点作为物资集中点，利用问题二三设计的算法计算各种聚类方式下的物资配送时间，最终我们以质心为条件进行 k-meams 聚类方法，得到使得物资中心配送时间最短的两个地点，即为应急物资集中点的最佳地点。

模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可

程序代码：

部分程序如下:

1 # 以下为floyd算法的实现代码
2 from math import *
3 import numpy as np
4 #创建节点字典
5 set_nodes={"v1":0,"v2":1,"v3":2,"v4":3,"v5":4,"v6":5,"v7":6,"v8":7,"v9":8,"v10":9,"v11":10,"v12"
:11,"v13":12,"v14":13}
6 INF = 999
7 #创建初始化距离矩阵
8 dis = np.array([[0, INF, INF, INF, 54, INF, 55, INF, INF, INF, 26, INF, INF, INF],
9 [INF, 0, 56, INF, 18, INF, INF, INF, INF, INF, INF, INF, INF, INF],
10 [INF, 56, 0, INF, 44, INF, INF, INF, INF, INF, INF, INF, INF, INF],
11 [INF, INF, INF, 0, INF, 28, INF, INF, INF, INF, INF, INF, INF, INF],
12 [54, 18, 44, INF, 0, 51, 34, 56, 48, INF, INF, INF, INF, INF],
13 [INF, INF, INF, 28, 51, 0, INF, INF, 27, 42, INF, INF, INF, INF],
14 [55, INF, INF, INF, 34, INF, 0, 36, INF, INF, INF, 38, INF, INF],
15 [INF, INF, INF, INF, 56, INF, 36, 0, 29, INF, INF, 33, INF, INF],
16 [INF, INF, INF, INF, 48, 27, INF, 29, 0, 61, INF, 29, 42, 36],
17 [INF, INF, INF, INF, INF, 42, INF, INF, 61, 0, INF, INF, INF, 25],
18 [26, INF, INF, INF, INF, INF, INF, INF, INF, INF, 0, 24, INF, INF],
19 [INF, INF, INF, INF, INF, INF, 38, 33, 29, INF, 24, 0, INF, INF],
20 [INF, INF, INF, INF, INF, INF, INF, INF, 42, INF, INF, INF, 0, 47],
21 [INF, INF, INF, INF, INF, INF, INF, INF, 36, 25, INF, INF, 47, 0]])
22 num = 14
23 #初始化一个矩阵 记录父节点 先令父节点为终点本身
24 parent=[[i for i in range(14)] for j in range(14)]
25
26 #核心代码
27 #i为中间节点
28 for i in range(num):
29 #j为起点
30 for j in range(num):
31 #k为终点
32 for k in range(num):
33 #更新最短距离
34 dis[j][k]= min(dis[j][k],dis[j][i]+dis[i][k])
35 parent[j][k]=parent[j][i]
36
37 #测试代码
38 if __name__ == ’__main__’:
39 for i in range(num):
40 # j为起点
41 print("[")
42 for j in range(num):
43 print(","+ str(dis[i][j]),end=’’)
44 print("],")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

1 # 以下为第一问的蚁群算法的求解代码
2 import random
3 import copy
4 import time
5 import sys
6 import math
7 import tkinter # //GUI模块
8 import threading
9 from functools import reduce
10 import matplotlib.pyplot as plt
11
12 (ALPHA, BETA, RHO, Q) = (1.0, 2.0, 0.5, 100.0)
13 # 城市数，蚁群
14 (city_num, ant_num) = (14, 50)
15 distance_x = [78, 278, 600, 700, 330, 550, 230, 380, 450, 720, 150, 330, 532, 700]
16 distance_y = [170, 100, 78, 151, 200, 220, 280, 300, 305, 300, 500, 550, 525, 500]
17 # 城市距离和信息素
18 distance_graph = [[0, 72, 98, 133, 54, 105, 55, 83, 79, 140, 26, 50, 121, 115],
19 [72, 0, 56, 97, 18, 69, 52, 74, 66, 111, 98, 90, 108, 102],
20 [98, 56, 0, 123, 44, 95, 78, 100, 92, 137, 124, 116, 134, 128],
21 [133, 97, 123, 0, 79, 28, 113, 84, 55, 70, 108, 84, 97, 91],
22 [54, 18, 44, 79, 0, 51, 34, 56, 48, 93, 80, 72, 90, 84],
23 [105, 69, 95, 28, 51, 0, 85, 56, 27, 42, 80, 56, 69, 63],
24 [55, 52, 78, 113, 34, 85, 0, 36, 65, 126, 62, 38, 107, 101],
25 [83, 74, 100, 84, 56, 56, 36, 0, 29, 90, 57, 33, 71, 65],
26 [79, 66, 92, 55, 48, 27, 65, 29, 0, 61, 53, 29, 42, 36],
27 [140, 111, 137, 70, 93, 42, 126, 90, 61, 0, 114, 90, 72, 25],
28 [26, 98, 124, 108, 80, 80, 62, 57, 53, 114, 0, 24, 95, 89],
29 [50, 90, 116, 84, 72, 56, 38, 33, 29, 90, 24, 0, 71, 65],
30 [121, 108, 134, 97, 90, 69, 107, 71, 42, 72, 95, 71, 0, 47],
31 [115, 102, 128, 91, 84, 63, 101, 65, 36, 25, 89, 65, 47, 0]]
32 pheromone_graph = [[1.0 for col in range(city_num)] for raw in range(city_num)]
33 x = []
34 y = []
35
36 # ----------- 蚂蚁 -----------
37 class Ant( object):
38 # 初始化
39 def __init__(self, ID):
40 self.ID = ID # ID
41 self.__clean_data() # 随机初始化出生点
42
43 # 初始数据
44 def __clean_data(self):
45 self.path = [] # 当前蚂蚁的路径
46 self.total_distance = 0.0 # 当前路径的总距离
47 self.move_count = 0 # 移动次数
48 self.current_city = -1 # 当前停留的城市
49 self.open_table_city = [True for i in range(city_num)] # 探索城市的状态
50 city_index = random.randint(0, city_num - 1) # 随机初始出生点
51 self.current_city = city_index
52 self.path.append(city_index)
53 self.open_table_city[city_index] = False
54 self.move_count = 1
55
56 # 选择下一个城市
57 def __choice_next_city(self):
58 next_city = -1
59 select_citys_prob = [0.0 for i in range(city_num)] # 存储去下个城市的概率
60 total_prob = 0.0
61 # 获取去下一个城市的概率
62 for i in range(city_num):
63 if self.open_table_city[i]:
64 try:
65 # 计算概率：与信息素浓度成正比，与距离成反比
66 select_citys_prob[i] = pow(pheromone_graph[self.current_city][i], ALPHA) *
pow(
67 (1.0 / distance_graph[self.current_city][i]), BETA)
68 total_prob += select_citys_prob[i]
69 except ZeroDivisionError as e:
70 print(’Ant ID: {ID}, current city: {current}, target city: {target}’.
format(ID=self.ID,current=self.current_city,target=i))
71 sys.exit(1)
72 # 轮盘选择城市
73 if total_prob > 0.0:
74 # 产生一个随机概率,0.0-total_prob
75 temp_prob = random.uniform(0.0, total_prob)
76 for i in range(city_num):
77 if self.open_table_city[i]:
78 # 轮次相减
79 temp_prob -= select_citys_prob[i]
80 if temp_prob < 0.0:
81 next_city = i
82 break
83 # 未从概率产生，顺序选择一个未访问城市
84 # if next_city == -1:
85 # for i in range(city_num):
86 # if self.open_table_city[i]:
87 # next_city = i
88 # break
89 if (next_city == -1):
90 next_city = random.randint(0, city_num - 1)
91 while ((self.open_table_city[next_city]) == False): # if==False,说明已经遍历过了
92 next_city = random.randint(0, city_num - 1)
93 # 返回下一个城市序号
94 return next_city
95
96 # 计算路径总距离
97 def __cal_total_distance(self):
98 temp_distance = 0.0
99 for i in range(1, city_num):
100 start, end = self.path[i], self.path[i - 1]
101 temp_distance += distance_graph[start][end]
102 # 回路
103 end = self.path[0]
104 temp_distance += distance_graph[start][end]
105 self.total_distance = temp_distance
106
107 # 移动操作
108 def __move(self, next_city):
109 self.path.append(next_city)
110 self.open_table_city[next_city] = False
111 self.total_distance += distance_graph[self.current_city][next_city]
112 self.current_city = next_city
113 self.move_count += 1
114
115 # 搜索路径
116 def search_path(self):
117 # 初始化数据
118 self.__clean_data()
119 # 搜素路径，遍历完所有城市为止
120 while self.move_count < city_num:
121 # 移动到下一个城市
122 next_city = self.__choice_next_city()
123 self.__move(next_city)
124 # 计算路径总长度
125 self.__cal_total_distance()
126
127
128 # ----------- TSP问题 -----------
129 class TSP( object):
130 def __init__(self, root, width=800, height=600, n=city_num):
131 # 创建画布
132 self.root = root
133 self.width = width
134 self.height = height
135 # 城市数目初始化为city_num
136 self.n = n
137 # tkinter.Canvas
138 self.canvas = tkinter.Canvas(
139 root,
140 width=self.width,
141 height=self.height,
142 bg="#EBEBEB", # 背景白色
143 xscrollincrement=1,
144 yscrollincrement=1
145 )
146 self.canvas.pack(expand=tkinter.YES, fill=tkinter.BOTH)
147 self.title("蚁群算法(n:初始化 e:开始搜索 s:停止搜索 q:退出程序)")
148 self.__r = 5
149 self.__lock = threading.RLock() # 线程锁
150 self.__bindEvents()
151 self.new()
152 # 计算城市之间的距离
153
154 # 按键响应程序
155 def __bindEvents(self):
156 self.root.bind("q", self.quite) # 退出程序
157 self.root.bind("n", self.new) # 初始化
158 self.root.bind("e", self.search_path) # 开始搜索
159 self.root.bind("s", self.stop) # 停止搜索
160
161 # 更改标题
162 def title(self, s):
163 self.root.title(s)
164
165 # 初始化
166 def new(self, evt=None):
167 # 停止线程
168 self.__lock.acquire()
169 self.__running = False
170 self.__lock.release()
171 self.clear() # 清除信息
172 self.nodes = [] # 节点坐标
173 self.nodes2 = [] # 节点对象
174 # 初始化城市节点
175 for i in range(city_num):
176 # 在画布上随机初始坐标
177 x = distance_x[i]
178 y = distance_y[i]
179 self.nodes.append((x, y))
180 # 生成节点椭圆，半径为self.__r
181 node = self.canvas.create_oval(x - 15,
182 y - 15, x + 15, y + 15,
183 fill="#FFFFE0", # 填充黄色
184 outline="#ff0000", # 轮廓红色
185 tags="node",
186 )
187 self.nodes2.append(node)
188 # 显示坐标
189 self.canvas.create_text(x, y, # 使用create_text方法在坐标（302，77）处绘制文字
190 text=i + 1, # 所绘制文字的内容
191 fill=’black’ # 所绘制文字的颜色为灰色
192 )
193 # 顺序连接城市
194 # self.line(range(city_num))
195 # 初始城市之间的距离和信息素
196 for i in range(city_num):
197 for j in range(city_num):
198 pheromone_graph[i][j] = 1.0
199 self.ants = [Ant(ID) for ID in range(ant_num)] # 初始蚁群
200 self.best_ant = Ant(-1) # 初始最优解
201 self.best_ant.total_distance = 1 << 31 # 初始最大距离
202 self. iter = 1 # 初始化迭代次数
203
204 # 将节点按order顺序连线
205 def line(self, order):
206 # 删除原线
207 self.canvas.delete("line")
208
209 def line2(i1, i2):
210 p1, p2 = self.nodes[i1], self.nodes[i2]
211 self.canvas.create_line(p1, p2, fill="#000000", tags="line")
212 return i2
213
214 # order[-1]为初始值
215 reduce(line2, order, order[-1])
216
217 # 清除画布
218 def clear(self):
219 for item in self.canvas.find_all():
220 self.canvas.delete(item)
221
222 # 退出程序
223 def quite(self, evt):
224 self.__lock.acquire()
225 self.__running = False
226 self.__lock.release()
227 self.root.destroy()
228 print(u"\n程序已退出...")
229 sys.exit()
230
231 # 停止搜索
232 def stop(self, evt):
233 self.__lock.acquire()
234 self.__running = False
235 self.__lock.release()
236 plt.rcParams[’font.sans-serif’] = [’SimHei’] # 指定默认字体
237 plt.rcParams[’axes.unicode_minus’] = False # 解决保存图像是负号’-’显示为方块的问题
238 plt.plot(x,y) # 当输入s停止搜索后，显示变化图像
239 plt.xlabel("迭代次数")
240 plt.ylabel("一次整体配送所花时间")
241 plt.show()
242
243 # 开始搜索
244 def search_path(self, evt=None):
245 # 开启线程
246 self.__lock.acquire()
247 self.__running = True
248 self.__lock.release()
249 while self.__running:
250 # 遍历每一只蚂蚁
251 for ant in self.ants:
252 # 搜索一条路径
253 ant.search_path()
254 # 与当前最优蚂蚁比较
255 if ant.total_distance < self.best_ant.total_distance:
256 # 更新最优解
257 self.best_ant = copy.deepcopy(ant)
258 # 更新信息素
259 self.__update_pheromone_gragh()
260 print(u"迭代次数：", self. iter, u"最佳路径总距离：",
int(self.best_ant.total_distance))
261 time = self.best_ant.total_distance/50
262 print("一次整体配送所花时间为：{:.4f}". format(time))
263 x.append(self. iter)
264 y.append(time)
265 # 连线
266 self.line(self.best_ant.path)
267 # 设置标题
268 self.title("TSP蚁群算法(n:随机初始 e:开始搜索 s:停止搜索 q:退出程序) 迭代次数: %d" %
self.
iter)
269 # 更新画布
270 self.canvas.update()
271 self. iter += 1
272
273 # 更新信息素
274 def __update_pheromone_gragh(self):
275 # 获取每只蚂蚁在其路径上留下的信息素
276 temp_pheromone = [[0.0 for col in range(city_num)] for raw in range(city_num)]
277 for ant in self.ants:
278 for i in range(1, city_num):
279 start, end = ant.path[i - 1], ant.path[i]
280 # 在路径上的每两个相邻城市间留下信息素，与路径总距离反比
281 temp_pheromone[start][end] += Q / ant.total_distance
282 temp_pheromone[end][start] = temp_pheromone[start][end]
283 # 更新所有城市之间的信息素，旧信息素衰减加上新迭代信息素
284 for i in range(city_num):
285 for j in range(city_num):
286 pheromone_graph[i][j] = pheromone_graph[i][j] * RHO + temp_pheromone[i][j]
287
288 # 主循环
289 def mainloop(self):
290 self.root.mainloop()
291
292
293 # ----------- 程序的入口处 -----------
294 if __name__ == ’__main__’:
295 TSP(tkinter.Tk()).mainloop()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可