图像降噪算法——从BM3D到VBM4D

图像降噪算法——从BM3D到VBM4D

BM3D算法是目前非AI降噪算法中最经典的算法之一，在BM3D的框架上改进得到的算法不计其数，这篇论文主要将BM3D算法的算法框架，在此基础上在结论中补充了下VBM3D算法和VBM4D算法。

1. 基本原理

BM3D算法的算法流程图如下所示：

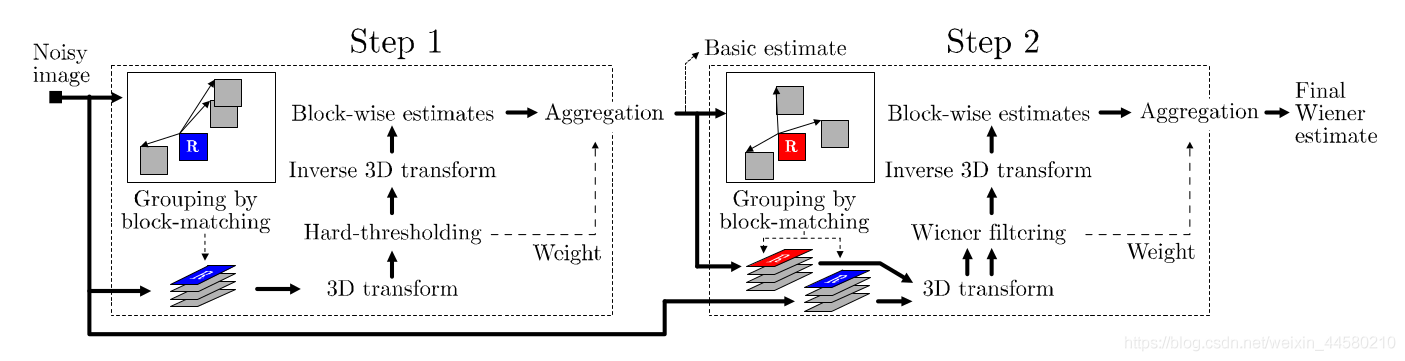
如图所示，算法一共分为两阶段，第一阶段主要实现了一个基于patch的硬阈值滤波，第二阶段主要实现了一个基于patch的维纳滤波，这里注意，BM3D的处理都是基于patch进行的，其中硬阈值滤波的过程只是一个预滤波的过程，而实际的降噪结果是来自于第二阶段的维纳滤波。下面我们对算法流程进行一个详细解释。
第一阶段：硬阈值滤波
（1）在原始噪声图像上，在目标patch周围搜索相似的图像patch，这里的相似定义为两个图像patch像素简单L2距离，将相似的patch组合成一个个group，这里要注意，在组合group的同时，需要记录group中的各个patch在原始图像上的坐标，因为在第一阶段结束的Aggregation过程中需要将降噪后的图像patch重构为原始的图像，论文中的这个示意图就很好地说明了这个过程2

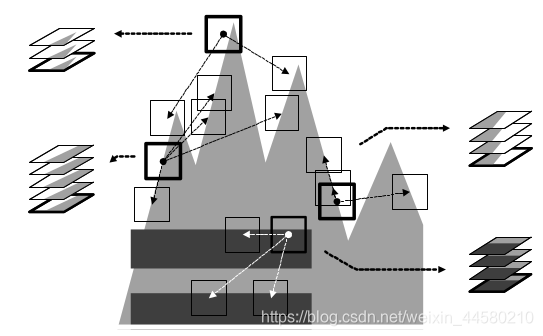
在论文中该过程抽象为如下两个公式：$$d^{\text{noisy }}\left(Z_{x_R},Z_x\right)=\frac{{\Vert Z_{x_R}-Z_x\Vert }_2^2}{{\left(N_1^{\mathrm{h}\mathrm{t}}\right)}^2}$$$$S_{x_R}^{\mathrm{h}\mathrm{t}}=\left\{x\in X:d\left(Z_{x_R},Z_x\right)\le {\tau }_{\text{match }}^{\mathrm{h}\mathrm{t}}\right\}$$

（2）接下来是在group上进行硬阈值滤波，硬阈值滤波相关的内容可以参考我之前的博客图像降噪算法——小波硬阈值滤波（上）和图像降噪算法——小波硬阈值滤波（下），大致原理是相同的。不同的是，因为这里的group是3D的元素结构，因此我们需要对group进行3D变换，3D变换是由一个2D的DCT变换或者Bior变换加上一个1D的Haar变换构成的。在3D变换的基础上进行硬阈值滤波，在完成硬阈值滤波后再进行3D反变换即可，该过程在论文中抽象为如下公式：$${\hat{\mathbf{Y}}}_{S_{x_R}^{\mathrm{h}\mathrm{t}}}={\mathcal{T}}_{3\mathrm{D}}^{{\mathrm{h}\mathrm{t}}^{-1}}\left({\rm Y}\left({\mathcal{T}}_{3\mathrm{D}}^{\mathrm{h}\mathrm{t}}\left({\mathbf{Z}}_{S_{x_R}^{\mathrm{h}\mathrm{t}}}\right)\right)\right)$$

（3）最后进行聚合(aggregation)操作，我们完成硬阈值滤波后得到仍然是一个个的group，聚合操作就是根据记录的各个patch中的坐标将group恢复成完整图像，在恢复过程中可能存在patch间overlap的情况，这时候会对patch的overlap部分进行加权平均，权重来自于硬阈值滤波过程中的系数

第二阶段：维纳滤波
（1）在第一阶段预降噪后的图像上，在目标patch周围搜索相似patch，然后构建group，公式如下：$$S_{x_R}^{\text{wie }}=\left\{x\in X:\frac{{\Vert {\hat{Y}}_{x_R}^{\text{basic }}-{\hat{Y}}_x^{\text{basic }}\Vert }_2^2}{{\left(N_1^{\text{wie }}\right)}^2}<{\tau }_{\text{match }}^{\text{wie }}\right\}$$不同的，因为第二阶段用到的是维纳滤波，我们一共需要构建两组group，第一组group就是如上所述的在预降噪图像上搜索得到的，第二组group是按照同样的坐标，在原始噪声图像进行构建。

（2）接下来是进行维纳滤波，维纳滤波的相关内容可以参考图像降噪算法——维纳滤波，维纳滤波公式如下：$${\mathbf{W}}_{S_{x_R}^{\text{wie }}}=\frac{{\left|{\mathcal{T}}_{3\mathrm{D}}^{\text{wie }}\left({\hat{\mathbf{Y}}}_{S_x^{\text{wie }}}^{\text{basic }}\right)\right|}^2}{{\left|{\mathcal{T}}_{3\mathrm{D}}^{\text{wie }}\left({\hat{\mathbf{Y}}}_{S_x^{\text{wic }}}^{\text{basic }}\right)\right|}^2+{\sigma }^2}$$$${\hat{\mathbf{Y}}}_{S_{x_R}^{wie}}={\mathcal{T}}_{3\mathrm{D}}^{{\mathrm{w}\mathrm{i}\mathrm{e}}^{-1}}\left({\mathbf{W}}_{S_{x_R}^{\text{wie }}}{\mathcal{T}}_{3\mathrm{D}}^{\text{wie }}\left({\mathbf{Z}}_{S_{x_R}^{\text{wie }}}\right)\right)$$可以看到，在维纳滤波我们是需要有输入图像的频谱作为降噪依据，在BM3D中就是采用第一阶段的预降噪图像作为输入图像

（3）最后同样是进行聚合(aggregation)操作，在overlap区域同样是进行加权平均，权重来自于维纳滤波系数，如下：$$w_{x_R}^{\text{wie }}={\sigma }^{-2}{\Vert {\mathbf{W}}_{S_{x_R}^{\text{wic }}}\Vert }_2^{-2}$$$${\hat{y}}^{\text{basic }}(x)=\frac{{\sum }_{x_R\in X}{\sum }_{x_m\in S_{x_R}^{\mathrm{h}\mathrm{t}}}{w}_{x_R}^{\mathrm{h}\mathrm{t}}{\hat{Y}}_{x_m}^{\mathrm{h}\mathrm{t},x_R}(x)}{{\sum }_{x_R\in X}{\sum }_{x_m\in S_{x_R}^{\mathrm{h}\mathrm{t}}}{w}_{x_R}^{\mathrm{h}\mathrm{t}}{\chi }_{x_m}(x)},\forall x\in X,$$
以上就是BM3D算法的全部流程，可以看出来，BM3D算法实际上就是维纳滤波，但是其结合了NLM的思想，通过寻找相似patch加强了降噪的效果。

2. python代码实现

开源的BM3D算法C++代码也有，但是写得通常都比较复杂，这里我参考BM3D ：稀疏三维变换域协同过滤的图像去噪||原理&算法实现提供一份python版本的实现，看完代码基本上就能屡清楚BM3D的实现过程了

# -*- coding: utf-8 -*-
"""
*BM3D算法简单实现,主要程序部分
"""
import cv2
import numpy
import math
import numpy.matlib

cv2.setUseOptimized(True)

# Parameters initialization
sigma = 25
Threshold_Hard3D = 2.7 * sigma  # Threshold for Hard Thresholding

Step1_Blk_Size = 4  # block_Size即块的大小
Step1_Blk_Step = 1  # Rather than sliding by one pixel to every next reference block, use a step of Nstep pixels in both horizontal and vertical directions.
Step1_Search_Step = 1  # 块的搜索step
First_Match_threshold = 125 * Step1_Blk_Size ** 2  # 用于计算block之间相似度的阈值
Step1_max_matched_cnt = 16  # 组最大匹配的块数
Step1_Search_Window = 15  # Search for candidate matching blocks in a local neighborhood of restricted size NS*NS centered

Step2_Blk_Size = 4
Step2_Blk_Step = 1
Step2_Search_Step = 1
Second_Match_threshold = 220. / 16 * Step2_Blk_Size ** 2  # 用于计算block之间相似度的阈值
Step2_max_matched_cnt = 32
Step2_Search_Window = 25

Beta_Kaiser = 1.5


def init(img, _blk_size, _Beta_Kaiser):
    """该函数用于初始化，返回用于记录过滤后图像以及权重的数组,还有构造凯撒窗"""
    m_shape = img.shape
    m_img = numpy.matrix(numpy.zeros(m_shape, dtype=float))
    m_wight = numpy.matrix(numpy.zeros(m_shape, dtype=float))

    # 窗函数(window function)是一种除在给定区间之外取值均为0的实函数
    K = numpy.matrix(numpy.kaiser(_blk_size, _Beta_Kaiser))
    m_Kaiser = numpy.array(K.T * K)  # 构造一个凯撒窗
    # 窗函数：https://zh.wikipedia.org/wiki/窗函数#Kaiser窗

    # print m_Kaiser, type(m_Kaiser), m_Kaiser.shape
    # cv2.imshow("Kaisser", m_Kaiser)
    # cv2.waitKey(0)
    # cv2.imwrite("Kaisser.jpg", m_Kaiser.astype(numpy.uint8))
    return m_img, m_wight, m_Kaiser


def Locate_blk(i, j, blk_step, block_Size, width, height):
    '''该函数用于保证当前的blk不超出图像范围'''
    if i * blk_step + block_Size < width:
        point_x = i * blk_step
    else:
        point_x = width - block_Size

    if j * blk_step + block_Size < height:
        point_y = j * blk_step
    else:
        point_y = height - block_Size

    m_blockPoint = numpy.array((point_x, point_y), dtype=int)  # 当前参考图像的顶点

    return m_blockPoint


def Define_SearchWindow(_noisyImg, _BlockPoint, _WindowSize, Blk_Size):
    """
    该函数利用block的左上顶点的位置返回一个二元组（x,y）
    用以界定_Search_Window左上角顶点坐标

    """
    point_x = _BlockPoint[0]  # 当前坐标
    point_y = _BlockPoint[1]  # 当前坐标

    # 获得SearchWindow四个顶点的坐标
    LX = point_x + Blk_Size / 2 - _WindowSize / 2  # 左上x
    LY = point_y + Blk_Size / 2 - _WindowSize / 2  # 左上y
    RX = LX + _WindowSize  # 右下x
    RY = LY + _WindowSize  # 右下y

    # 判断一下是否越界
    if LX < 0:
        LX = 0
    elif RX > _noisyImg.shape[0]:
        LX = _noisyImg.shape[0] - _WindowSize
    if LY < 0:
        LY = 0
    elif RY > _noisyImg.shape[0]:
        LY = _noisyImg.shape[0] - _WindowSize

    return numpy.array((LX, LY), dtype=int)


def Step1_fast_match(_noisyImg, _BlockPoint):
    """快速匹配"""
    '''
    *返回邻域内寻找和当前_block相似度最高的几个block,返回的数组中包含本身
    *_noisyImg:噪声图像
    *_BlockPoint:当前block的坐标及大小
    '''
    (present_x, present_y) = _BlockPoint  # 当前坐标
    Blk_Size = Step1_Blk_Size
    Search_Step = Step1_Search_Step
    Threshold = First_Match_threshold
    max_matched = Step1_max_matched_cnt
    Window_size = Step1_Search_Window

    blk_positions = numpy.zeros((max_matched, 2), dtype=int)  # 用于记录相似blk的位置
    Final_similar_blocks = numpy.zeros((max_matched, Blk_Size, Blk_Size), dtype=float)  # 用于保存最后结果

    img = _noisyImg[present_x: present_x + Blk_Size, present_y: present_y + Blk_Size]
    dct_img = cv2.dct(img.astype(numpy.float64))  # 对目标作block作二维余弦变换

    Final_similar_blocks[0, :, :] = dct_img  # 保存变换后的目标块
    blk_positions[0, :] = _BlockPoint

    Window_location = Define_SearchWindow(_noisyImg, _BlockPoint, Window_size, Blk_Size)
    blk_num = (Window_size - Blk_Size) / Search_Step  # 确定最多可以找到多少相似blk
    blk_num = int(blk_num)
    (present_x, present_y) = Window_location

    similar_blocks = numpy.zeros((blk_num ** 2, Blk_Size, Blk_Size), dtype=float)
    m_Blkpositions = numpy.zeros((blk_num ** 2, 2), dtype=int)
    Distances = numpy.zeros(blk_num ** 2, dtype=float)  # 记录各个blk与它的相似度

    # 开始在_Search_Window中搜索,初始版本先采用遍历搜索策略,这里返回最相似的几块
    matched_cnt = 0
    for i in range(blk_num):
        for j in range(blk_num):
            tem_img = _noisyImg[present_x: present_x + Blk_Size, present_y: present_y + Blk_Size]
            dct_Tem_img = cv2.dct(tem_img.astype(numpy.float64))
            # 先对块进行dct变换再求l2-norm，寻找相似块，降低噪点的干扰
            m_Distance = numpy.linalg.norm((dct_img - dct_Tem_img)) ** 2 / (Blk_Size ** 2)

            # 下面记录数据自动不考虑自身(因为已经记录)
            if m_Distance < Threshold and m_Distance > 0:  # 说明找到了一块符合要求的
                similar_blocks[matched_cnt, :, :] = dct_Tem_img
                m_Blkpositions[matched_cnt, :] = (present_x, present_y)
                Distances[matched_cnt] = m_Distance
                matched_cnt += 1
            present_y += Search_Step
        present_x += Search_Step
        present_y = Window_location[1]  # 搜索窗的行
    # 取前matched_cnt个块
    Distances = Distances[:matched_cnt]
    # 对distance进行排序，找到对应顺序的序号
    # numpy.argsort() 的用法：
    # https://docs.scipy.org/doc/numpy/reference/generated/numpy.argsort.html
    Sort = Distances.argsort()

    # 统计一下找到了多少相似的blk
    if matched_cnt < max_matched:
        Count = matched_cnt + 1
    else:
        Count = max_matched
    # 将前matched_cnt个块放入Final_similar_blocks，左上坐标信息保存在lk_positions
    if Count > 0:
        for i in range(1, Count):
            Final_similar_blocks[i, :, :] = similar_blocks[Sort[i - 1], :, :]
            blk_positions[i, :] = m_Blkpositions[Sort[i - 1], :]
    return Final_similar_blocks, blk_positions, Count


def Step1_3DFiltering(_similar_blocks):
    '''
    *3D变换及滤波处理
    *_similar_blocks:相似的一组block,这里已经是频域的表示
    *要将_similar_blocks第三维依次取出,然在频域用阈值滤波之后,再作反变换
    '''

    statis_nonzero = 0  # 非零元素个数
    m_Shape = _similar_blocks.shape

    # 下面这一段代码很耗时
    for i in range(m_Shape[1]):
        for j in range(m_Shape[2]):
            # print _similar_blocks[:, i, j], type(_similar_blocks[:, i, j])
            tem_Vct_Trans = cv2.dct(_similar_blocks[:, i, j])
            # 硬阈值变换，去掉较小的频率成分
            tem_Vct_Trans[numpy.abs(tem_Vct_Trans[:]) < Threshold_Hard3D] = 0.
            statis_nonzero += tem_Vct_Trans.nonzero()[0].size
            _similar_blocks[:, i, j] = cv2.idct(tem_Vct_Trans)[0]
    return _similar_blocks, statis_nonzero


def Aggregation_hardthreshold(_similar_blocks, blk_positions, m_basic_img, m_wight_img, _nonzero_num, Count, Kaiser):
    '''
    *对3D变换及滤波后输出的stack进行加权累加,得到初步滤波的图片
    *_similar_blocks:相似的一组block,这里是频域的表示
    *对这些块，用非零项的权重乘以凯撒窗之后再分别放回原位
    '''
    _shape = _similar_blocks.shape
    if _nonzero_num < 1:
        _nonzero_num = 1
    block_wight = (1. / (sigma ** 2 * _nonzero_num)) * Kaiser
    for i in range(Count):
        point = blk_positions[i, :]
        tem_img = block_wight * cv2.idct(_similar_blocks[i, :, :])
        m_basic_img[point[0]:point[0] + _shape[1], point[1]:point[1] + _shape[2]] += tem_img
        m_wight_img[point[0]:point[0] + _shape[1], point[1]:point[1] + _shape[2]] += block_wight


def BM3D_1st_step(_noisyImg):
    """第一步,基本去噪"""
    # 初始化一些参数：
    (width, height) = _noisyImg.shape  # width = row, height = col
    block_Size = Step1_Blk_Size  # 块大小
    blk_step = Step1_Blk_Step  # N块步长滑动
    # 根据步长确定搜索的次数
    Width_num = (width - block_Size) / blk_step
    Height_num = (height - block_Size) / blk_step

    # 初始化几个数组
    # 空图像、空权重表、凯撒窗
    Basic_img, m_Wight, m_Kaiser = init(_noisyImg, Step1_Blk_Size, Beta_Kaiser)

    # 开始逐block的处理,+2是为了避免边缘上不够
    for i in range(int(Width_num + 2)):
        for j in range(int(Height_num + 2)):
            # m_blockPoint当前参考图像的左上角顶点
            m_blockPoint = Locate_blk(i, j, blk_step, block_Size, width, height)  # 该函数用于保证当前的blk不超出图像范围
            Similar_Blks, Positions, Count = Step1_fast_match(_noisyImg, m_blockPoint)  # 相似块集合、相似块位置、相似块数量
            Similar_Blks, statis_nonzero = Step1_3DFiltering(Similar_Blks)  # 协同过滤后的相似块集合、非零项数量
            Aggregation_hardthreshold(Similar_Blks, Positions, Basic_img, m_Wight, statis_nonzero, Count, m_Kaiser)
    Basic_img[:, :] /= m_Wight[:, :]
    basic = numpy.matrix(Basic_img, dtype=int)
    basic.astype(numpy.uint8)

    return basic


def Step2_fast_match(_Basic_img, _noisyImg, _BlockPoint):
    '''
    *快速匹配算法,返回邻域内寻找和当前_block相似度最高的几个block,要同时返回basicImg和IMG
    *_Basic_img: 基础去噪之后的图像
    *_noisyImg:噪声图像
    *_BlockPoint:当前block的坐标及大小
    '''
    (present_x, present_y) = _BlockPoint  # 当前坐标
    Blk_Size = Step2_Blk_Size
    Threshold = Second_Match_threshold
    Search_Step = Step2_Search_Step
    max_matched = Step2_max_matched_cnt
    Window_size = Step2_Search_Window

    blk_positions = numpy.zeros((max_matched, 2), dtype=int)  # 用于记录相似blk的位置
    Final_similar_blocks = numpy.zeros((max_matched, Blk_Size, Blk_Size), dtype=float)
    Final_noisy_blocks = numpy.zeros((max_matched, Blk_Size, Blk_Size), dtype=float)

    img = _Basic_img[present_x: present_x + Blk_Size, present_y: present_y + Blk_Size]
    dct_img = cv2.dct(img.astype(numpy.float32))  # 对目标作block作二维余弦变换
    Final_similar_blocks[0, :, :] = dct_img

    n_img = _noisyImg[present_x: present_x + Blk_Size, present_y: present_y + Blk_Size]
    dct_n_img = cv2.dct(n_img.astype(numpy.float32))  # 对目标作block作二维余弦变换
    Final_noisy_blocks[0, :, :] = dct_n_img

    blk_positions[0, :] = _BlockPoint

    Window_location = Define_SearchWindow(_noisyImg, _BlockPoint, Window_size, Blk_Size)
    blk_num = (Window_size - Blk_Size) / Search_Step  # 确定最多可以找到多少相似blk
    blk_num = int(blk_num)
    (present_x, present_y) = Window_location

    similar_blocks = numpy.zeros((blk_num ** 2, Blk_Size, Blk_Size), dtype=float)
    m_Blkpositions = numpy.zeros((blk_num ** 2, 2), dtype=int)
    Distances = numpy.zeros(blk_num ** 2, dtype=float)  # 记录各个blk与它的相似度

    # 开始在_Search_Window中搜索,初始版本先采用遍历搜索策略,这里返回最相似的几块
    matched_cnt = 0
    for i in range(blk_num):
        for j in range(blk_num):
            tem_img = _Basic_img[present_x: present_x + Blk_Size, present_y: present_y + Blk_Size]
            # dct_Tem_img = cv2.dct(tem_img.astype(numpy.float32))
            # m_Distance = numpy.linalg.norm((dct_img - dct_Tem_img)) ** 2 / (Blk_Size ** 2)

            m_Distance = numpy.linalg.norm((img - tem_img)) ** 2 / (Blk_Size ** 2)
            # 下面记录数据自动不考虑自身(因为已经记录)
            if m_Distance < Threshold and m_Distance > 0:
                dct_Tem_img = cv2.dct(tem_img.astype(numpy.float32))
                similar_blocks[matched_cnt, :, :] = dct_Tem_img
                m_Blkpositions[matched_cnt, :] = (present_x, present_y)
                Distances[matched_cnt] = m_Distance
                matched_cnt += 1
            present_y += Search_Step
        present_x += Search_Step
        present_y = Window_location[1]
    Distances = Distances[:matched_cnt]
    Sort = Distances.argsort()

    # 统计一下找到了多少相似的blk
    if matched_cnt < max_matched:
        Count = matched_cnt + 1
    else:
        Count = max_matched

    # nosiy图像的3D Stack，利用第一步的Basic估计结果来构造
    if Count > 0:
        for i in range(1, Count):
            Final_similar_blocks[i, :, :] = similar_blocks[Sort[i - 1], :, :]
            blk_positions[i, :] = m_Blkpositions[Sort[i - 1], :]

            (present_x, present_y) = m_Blkpositions[Sort[i - 1], :]
            n_img = _noisyImg[present_x: present_x + Blk_Size, present_y: present_y + Blk_Size]
            Final_noisy_blocks[i, :, :] = cv2.dct(n_img.astype(numpy.float64))

    return Final_similar_blocks, Final_noisy_blocks, blk_positions, Count


def Step2_3DFiltering(_Similar_Bscs, _Similar_Imgs):
    '''
    *3D维纳变换的协同滤波
    *_similar_blocks:相似的一组block,这里是频域的表示
    *要将_similar_blocks第三维依次取出,然后作dct,在频域进行维纳滤波之后,再作反变换
    *返回的Wiener_wight用于后面Aggregation
    '''
    m_Shape = _Similar_Bscs.shape
    Wiener_wight = numpy.zeros((m_Shape[1], m_Shape[2]), dtype=float)

    for i in range(m_Shape[1]):
        for j in range(m_Shape[2]):
            tem_vector = _Similar_Bscs[:, i, j]
            tem_Vct_Trans = numpy.matrix(cv2.dct(tem_vector))

            Norm_2 = numpy.float64(tem_Vct_Trans.T * tem_Vct_Trans)
            m_weight = Norm_2 / (Norm_2 + sigma ** 2)
            Wiener_wight[i, j] = m_weight

            #if m_weight != 0: Wiener_wight[i, j] = 1. / (m_weight ** 2 * sigma ** 2)
            # else:
            #     Wiener_wight[i, j] = 10000

            # RES=IDCT(WEIGHT(DCT(NOISE_BLOCK)))
            tem_vector = _Similar_Imgs[:, i, j]
            tem_Vct_Trans = m_weight * cv2.dct(tem_vector)
            _Similar_Bscs[:, i, j] = cv2.idct(tem_Vct_Trans)[0]

    return _Similar_Bscs, Wiener_wight


def Aggregation_Wiener(_Similar_Blks, _Wiener_wight, blk_positions, m_basic_img, m_wight_img, Count, Kaiser):
    '''
    *对3D变换及滤波后输出的stack进行加权累加,得到初步滤波的图片
    *_similar_blocks:相似的一组block,这里是频域的表示
    *对于最后的块，乘以凯撒窗之后再输出
    '''
    _shape = _Similar_Blks.shape
    block_wight = _Wiener_wight * Kaiser

    for i in range(Count):
        point = blk_positions[i, :]
        tem_img = _Wiener_wight * cv2.idct(_Similar_Blks[i, :, :]) * Kaiser
        m_basic_img[point[0]:point[0] + _shape[1], point[1]:point[1] + _shape[2]] += tem_img
        m_wight_img[point[0]:point[0] + _shape[1], point[1]:point[1] + _shape[2]] += block_wight


def BM3D_2nd_step(_basicImg, _noisyImg):
    '''Step 2. 最终的估计: 利用基本的估计，进行改进了的分组以及协同维纳滤波'''
    # 初始化一些参数：
    (width, height) = _noisyImg.shape
    block_Size = Step2_Blk_Size
    blk_step = Step2_Blk_Step
    Width_num = (width - block_Size) / blk_step
    Height_num = (height - block_Size) / blk_step

    # 初始化几个数组
    m_img, m_Wight, m_Kaiser = init(_noisyImg, block_Size, Beta_Kaiser)

    for i in range(int(Width_num + 2)):
        for j in range(int(Height_num + 2)):
            m_blockPoint = Locate_blk(i, j, blk_step, block_Size, width, height)
            Similar_Blks, Similar_Imgs, Positions, Count = Step2_fast_match(_basicImg, _noisyImg, m_blockPoint)
            Similar_Blks, Wiener_wight = Step2_3DFiltering(Similar_Blks, Similar_Imgs)
            Aggregation_Wiener(Similar_Blks, Wiener_wight, Positions, m_img, m_Wight, Count, m_Kaiser)
    m_img[:, :] /= m_Wight[:, :]
    Final = numpy.matrix(m_img, dtype=int)
    Final.astype(numpy.uint8)

    return Final


def Gauss_noise(img, sigma=25):
    noise = numpy.matlib.randn(img.shape) * sigma
    res = img + noise
    return res


def PSNR(img1, img2):
    D = numpy.array(img1 - img2, dtype=numpy.int64)
    D[:, :] = D[:, :] ** 2
    RMSE = D.sum() / img1.size
    psnr = 10 * math.log10(float(255. ** 2) / RMSE)
    return psnr


if __name__ == '__main__':
    cv2.setUseOptimized(True)  # OpenCV 中的很多函数都被优化过（使用 SSE2，AVX 等）。也包含一些没有被优化的代码。使用函数 cv2.setUseOptimized() 来开启优化。
    img_name = "./len128*128.jpg"  # 图像的路径
    ori = cv2.imread(img_name, cv2.IMREAD_GRAYSCALE)  # 读入图像，cv2.IMREAD_GRAYSCALE:以灰度模式读入图像
    cv2.imwrite("ori.jpg", ori)
    img = Gauss_noise(ori)
    cv2.imwrite("noise.jpg", img)

    print 'The PSNR After add noise %f' % PSNR(ori, img)
    # 记录程序运行时间
    e1 = cv2.getTickCount()  # cv2.getTickCount 函数返回从参考点到这个函数被执行的时钟数
    # if(img is not None):
    #     print("success")
    Basic_img = BM3D_1st_step(img)
    e2 = cv2.getTickCount()
    time = (e2 - e1) / cv2.getTickFrequency()  # 计算函数执行时间
    print ("The Processing time of the First step is %f s" % time)
    cv2.imwrite("Basic3.jpg", Basic_img)

    print ("The PSNR between the two img of the First step is %f" % PSNR(ori, Basic_img))

    # Basic_img = cv2.imread("Basic3.jpg", cv2.IMREAD_GRAYSCALE)

    Final_img = BM3D_2nd_step(Basic_img, img)
    e3 = cv2.getTickCount()
    time = (e3 - e2) / cv2.getTickFrequency()
    print ("The Processing time of the Second step is %f s" % time)
    cv2.imwrite("Final3.jpg", Final_img)

    print ("The PSNR between the two img of the Second step is %f" % PSNR(ori, Final_img))
    time = (e3 - e1) / cv2.getTickFrequency()
    print ("The total Processing time is %f s" % time)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429

3. 结论

从BM3D提出之后，学术界就在BM3D的基础上涌现了一批类似的方法，例如最近2019年和2020年的唯一的两篇最新的TIP上的传统算法NLH和ACVA都是在BM3D的基础上改进的，还有一条很有意思的pipeline，就是BM3D -> BM4D -> VBM3D -> VBM4D这几个算法，其中：
BM4D算法框架如下：

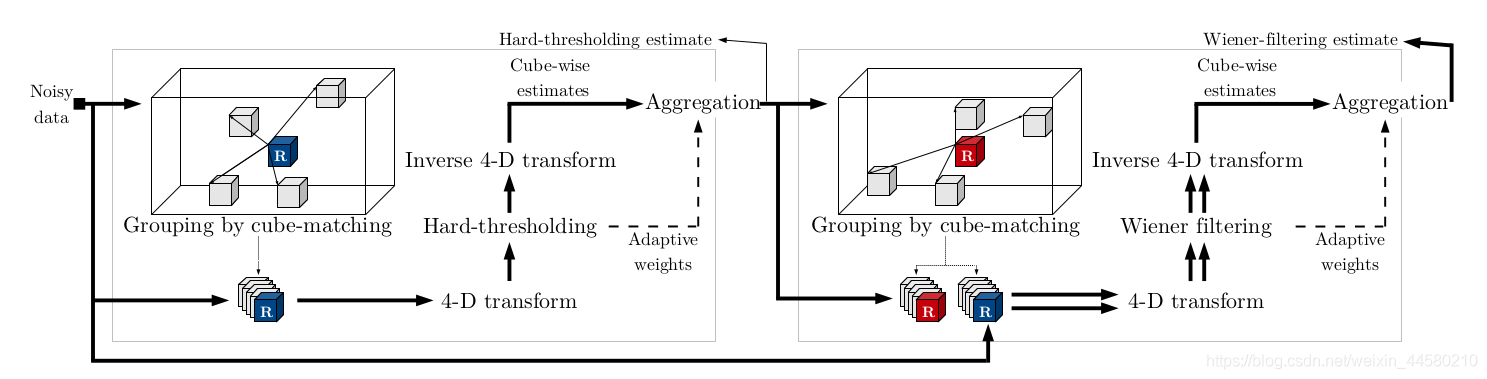
该算法仍然输入单帧降噪算法，不过对象不是二维图像，而是三维体素，在方法上应该没有什么太大的区别。

VBM3D算法框架如下：

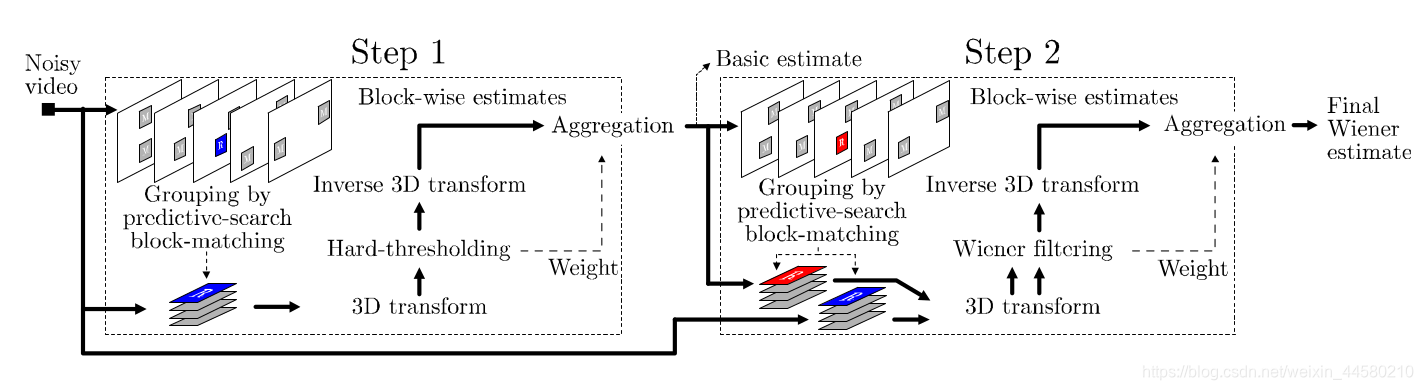
该算法属于时域去噪，在方法上没有太大的改变，如上图所示，只是在寻找相似patch时不是在单张图像上搜索，而是在相邻的若干张图像上进行搜索，仅仅是这样的变化，VBM3D也成了时域降噪领域里程碑式的算法，由此可见该算法的强大

VBM4D算法和VBM3D的算法主要的区别在于该算法对图像patch进行了对齐，此外在域变换的操作上也有相应的改进，具体的细节就不在此赘述了。

在工业界上，因为BM3D的计算量比较大，虽然效果好但实际用起来也确实很困难，在GPU上实现也很难达到实时，华为的麒麟芯片对该算法进行了硬化才达到实时降噪的效果

此外，这里我写一个各种算法的总结目录图像降噪算法——图像降噪算法总结，对图像降噪算法感兴趣的同学欢迎参考