快速排序(Quick Sort)(C语言) 超详细解析!!!

生活的本质是什么呢? 无非就是你要什么就不给你什么. 而生活的智慧是什么呢? 是给你什么就用好什么. ---马斯克

---

正文开始

一. 前言

接上文, 前面我们了解了插入排序, 与优化版本希尔排序, 那么本篇博客将详细介绍另外一种排序, 快速排序.

博客主页: 酷酷学!!!

感谢关注~

二. 快速排序的概念

快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，

其基本思想为：

任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

三. 快速排序的实现

将区间按照基准值划分为左右两半部分的常见方式有三种版本

1. hoare

如图所示, 排序的思想为

第一步:
两个下标, 一个从后往前走, 一个从前往后走, 然后定义一个基准值key, 下表为keyi,这里要注意要保证end先走, 才能让最后相遇的位置小于keyi的位置, 因为end先走无非就两种情况, 第一种, end找到了比key小的值, 停下来, 最后一次begin相遇end,交换相遇结点与key结点, 第二种情况, end相遇begin, 此时end没有找到比keyi小的值, 然后最后一次与begin相遇, 此时begin的值为上一次交换后的值, 所以比keyi小.然后相遇与keyi交换位置, 此时6这个位置就排好了

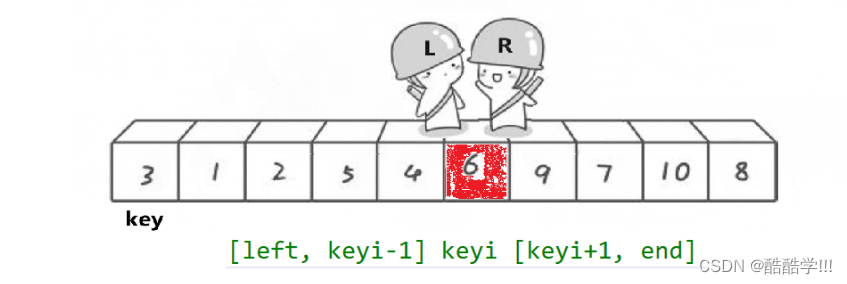
第二步:

因为6这个位置排好了, 所以进行下一次的排序,以6划分为两个区域,然后再次递归调用函数, 如果最后的区间不存在或者只有一个值那么就结束函数.当left==right时此时区间只有一个值就不需要排序, 区间不存在也不需要排序.

void QuickSort(int* a, int left, int right)
{
	if (left >= right)
	{
		return;
	}
	int keyi = left;
	int begin = left,end = right;
	while (begin < end)
	{

		while (begin < end && a[end] >= a[keyi])
		{
			end--;
		}
		while (begin < end && a[begin] <= a[keyi])
		{
			begin++;
		}
		Swap(&a[begin], &a[end]);
	}

	Swap(&a[begin], &a[keyi]);
	keyi = begin;

	QuickSort(a, left, keyi - 1);
	QuickSort(a, keyi + 1, right);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

我们来分析一下快速排序的时间复杂度, 目前来看, 每一层的时间复杂度为O(N), 高度为logn, 所以时间复杂度为O(NlogN), 但是这是在较好的情况下, 也就是相当于二叉树, 左右区间差不多大, 那么如果是有序的一系列数字, 那么这个排序就很不友好, 很容易栈溢出,递归层次很深, 就不是logn, 那么如何进行优化呢, 就需要我们修改它的key值, 不大不小为最好的情况, 为了避免有序情况下，效率退化, 可以选择 随机选key法 或者 三数取中法

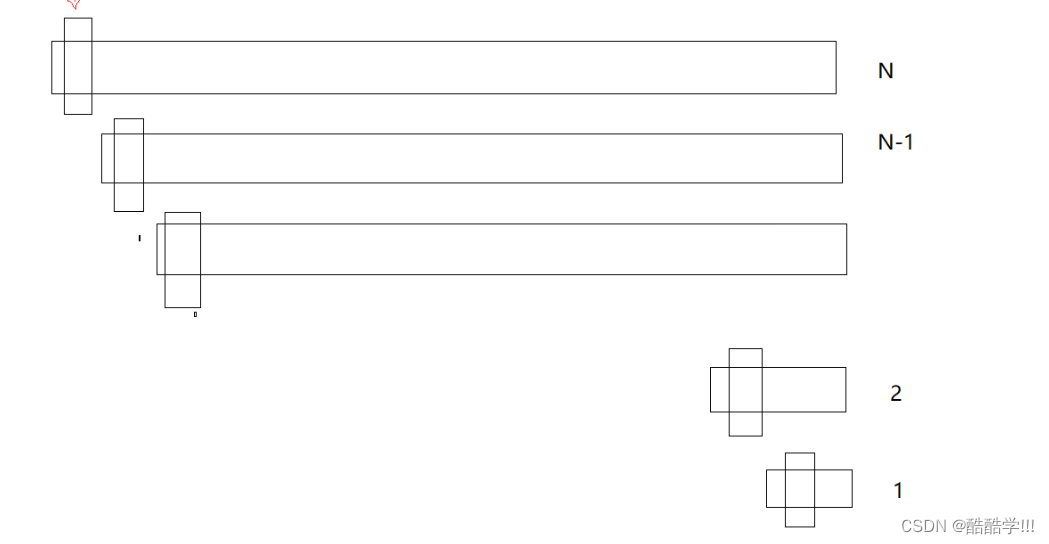
这里我们来介绍一下三数取中法的优化.

int GetMidi(int* a, int left, int right)
{
	int midi = (right - left) / 2;
	if (a[left] < a[midi])
	{
		if (a[midi] < a[right])
		{
			return midi;
		}
		else if(a[left] < a[right])
		{
			return right;
		}
		else
		{
			return left;
		}
	}
	else//a[left] > a[midi]
	{
		if (a[left] < a[right])
		{
			return left;
		}
		else if (a[midi] > a[right])
		{
			return midi;
		}
		else
		{
			return right;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

我们可以定义一个函数, 然后选取区间内最左边的值, 最右边的值, 中间的值,那个不大又不小的值作为key, 利用上述函数, 我们的代码可以改写为

void QuickSort(int* a, int left, int right)
{

	if (left >= right)
	{
		return;
	}

	//三数取中
	int midi = GetMidi(a, left, right);
	Swap(&a[left], &a[midi]);

	int keyi = left;
	int begin = left,end = right;
	while (begin < end)
	{

		while (begin < end && a[end] >= a[keyi])
		{
			end--;
		}
		while (begin < end && a[begin] <= a[keyi])
		{
			begin++;
		}
		Swap(&a[begin], &a[end]);
	}

	Swap(&a[begin], &a[keyi]);
	keyi = begin;

	QuickSort(a, left, keyi - 1);
	QuickSort(a, keyi + 1, right);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

有了上述的优化, 我们的代码效率就算在有序的情况下也能大大的提升效率, 但是还有一个问题, 我们知道, 二叉树中递归调用, 最后一层递归调用的次数占据了总调用次数的一半, 我们可以把最后几层的递归调用优化掉, 如果区间为十个数那么我们选择其他的排序方法, 如果选堆排序, 十个数还需要建堆比较麻烦, 如果使用希尔排序, 那么就是多此一举, 数据量不大选择希尔排序属实有点浪费了, 那我们就在时间复杂度为O(N^2)的排序中选择一个相对来说效率比较高的插入排序.优化后的代码如下:

void QuickSort(int* a, int left, int right)
{

	if (left >= right)
	{
		return;
	}
	if ((right - left + 1) < 10)
	{
		InsertSort(a + left, right - left + 1);
	}
	else
	{
		//三数取中
		int midi = GetMidi(a, left, right);
		Swap(&a[left], &a[midi]);

		int keyi = left;
		int begin = left, end = right;
		while (begin < end)
		{

			while (begin < end && a[end] >= a[keyi])
			{
				end--;
			}
			while (begin < end && a[begin] <= a[keyi])
			{
				begin++;
			}
			Swap(&a[begin], &a[end]);
		}

		Swap(&a[begin], &a[keyi]);
		keyi = begin;

		QuickSort(a, left, keyi - 1);
		QuickSort(a, keyi + 1, right);
	}

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

此优化在release版本下较为突出.

2. 挖坑法

前面单趟排序的方法由hoare发明之后又有另外的一种排序方法, 挖坑法, 它的思路比hoare排序的思想更容易理解

//挖坑法
int PartSort3(int* a, int left, int right)
{
	//三数取中
	int midi = GetMidi(a, left, right);
	Swap(&a[left], &a[midi]);
	int keyi = left;

	int begin = left, end = right;
	int tmp = a[keyi];
	while (begin < end)
	{
		while (begin < end && a[end] >= a[keyi])
		{
			end--;
		}
		a[keyi] = a[end];
		keyi = end;
		while (begin < end && a[begin] <= a[end])
		{
			begin++;
		}
		a[keyi] = a[begin];
		keyi = begin;
	}
	a[keyi] = tmp;
	return keyi;
}

void QuickSort(int* a, int left, int right)
{
	if (left >= right)
	{
		return;
	}

	if (right - left + 1 < 10)
	{
		InsertSort(a + left, right - left + 1);
	}
	
	int keyi = PartSort3(a,left,right);

	QuickSort(a, left, keyi - 1);
	QuickSort(a, keyi + 1, right);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

我们可以直接把单趟排序的算法拿出来封装成一个函数, 如图所示挖坑法特别好理解, 先让keyi的值存放在一个临时变量中, 挖一个坑,先让对面的先走, 如果遇到比end小的就把它拿出来填入坑中, 然后begin在开始走, 遇到大的填入坑中, 这样依次轮换,相遇时将keyi的值填入坑中.

3. 前后指针法

如图所示, 初始时, prev指针指向序列开头, cur指针指向prev指针的后一个位置, 然后判断cur指针指向的数据是否小于key, 则prev指针后移一位, 并于cur指针指向的内容交换, 然后cur++,cur指针指向的数据仍然小于key,步骤相同, 如果cur指针指向的数据大于key, 则继续++,最后如果cur指针已经越界, 这时我们将prev指向的内容与key进行交换.

可以看到也就是一个不断轮换的过程, 将大的数依次往后翻转, 小的数往前挪动, 这种方法代码写起来简洁, 当然我们也可以优化一下, 让cur和prev相等时就没必要进行交换

//前后指针版
int PartSort2(int* a, int left, int right)
{
	//三数取中
	int midi = GetMidi(a, left, right);
	Swap(&a[left], &a[midi]);
	int keyi = left;

	int prev = left;
	int cur = prev + 1;
	while (cur <= right)
	{
		if (a[cur] < a[keyi] && prev++ != cur)
		{
			Swap(&a[cur], &a[prev]);
		}
		cur++;
	}
	Swap(&a[prev], &a[keyi]);
	return prev;
}

void QuickSort(int* a, int left, int right)
{
	if (left >= right)
	{
		return;
	}

	if (right - left + 1 < 10)
	{
		InsertSort(a + left, right - left + 1);
	}
	
	int keyi = PartSort2(a,left,right);

	QuickSort(a, left, keyi - 1);
	QuickSort(a, keyi + 1, right);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

以上是递归版本的实现, 那么我们知道, 递归层次太深会容易栈溢出, 那么能不能采用非递归的实现呢, 答案肯定是可以的, 我们可以使用栈这个数据结果, 然后将区间入栈中, 栈不为空循环对区间进行排序, 一般linux系统下函数栈帧的空间的大小为8M, 而堆空间大小为2G, 所以这个空间是非常大的, 而且栈也是动态开辟的空间, 在堆区申请, 所以几乎不需要考虑空间不够, 我们可以将区间压栈, 先压入右区间, 在压入左区间, 然后排序的时候先排完左区间再排右区间, 这是一种深度优先算法(DFS), 当然也可以创建队列, 那么走的就是一层一层的排序, 每一层的左右区间都排序, 是一种广度优先算法(BFS).
代码实现:

这里可以创建一个结构体变量存放区间, 也可以直接压入两次, 分别把左值和右值压入

//非递归版
#include"stack.h"
void QuickSortNonR(int* a, int left, int right)
{
	ST st;
	STInit(&st);
	STPush(&st, right);
	STPush(&st, left);
	while (!STEmpty(&st))
	{
		int begin = STTop(&st);
		STPop(&st);
		int end = STTop(&st);
		STPop(&st);

		int keyi = PartSort1(a, begin, end);
		//[begin,keyi-1] keyi [keyi+1,end]
		//先压入右区间
		if (keyi + 1 < end)
		{
			STPush(&st, end);
			STPush(&st, keyi + 1);
		}
		if (begin < keyi - 1)
		{
			STPush(&st, keyi - 1);
			STPush(&st, begin);
		}
	}
	Destroy(&st);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

总结

快速排序是一种常用的排序算法，其时间复杂度为O(nlogn)。它的基本思想是通过一趟排序将待排序序列分割成独立的两部分，其中一部分的所有元素都比另一部分的所有元素小，然后再对这两部分分别进行排序，最终得到一个有序序列。

---

完

期待支持, 感谢关注~