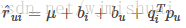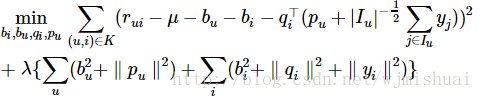推荐系统 | 协同过滤 —— 矩阵降维SVD/SVD++

目录

1.特征值分解（EVD）

1.1.实对称矩阵（也可为方阵）

 1.2.一般矩阵

2.奇异值分解（SVD）

2.1.奇异值分解定义

2.2.奇异值求解

2.3.数学引例

2.4.图像压缩应用（Python）

2.5.协同过滤推荐系统中矩阵分解应用

3.SVD++

3.1. 增加偏执项的SVD

3.2.SVD++

---

奇异值分解（SVD）在数据降维中应用较多

1.特征值分解（EVD）

1.1.实对称矩阵（也可为方阵）

 1.2.一般矩阵

2.奇异值分解（SVD）

2.1.奇异值分解定义

2.2.奇异值求解

2.3.数学引例

2.4.图像压缩应用（Python）

# ! /usr/bin/env python
# coding:utf-8
# python interpreter:3.6.2
# author: admin_maxin
import numpy as np
import cv2
import matplotlib.pyplot as plt
 
 
img = cv2.imread("dollar.jpg", cv2.IMREAD_GRAYSCALE)
# 图像大小351x499x3
print(img.shape)
 
# SVD
# 从svd函数中得到的奇异值sigma它是从大到小排列的
U, sigma, VT = np.linalg.svd(img)
 
# 取奇异值重构图片
range_1 = 6
img_1 = (U[:, 0:range_1]).dot(np.diag(sigma[0:range_1])).dot(VT[0:range_1, :])
 
range_2 = 120
img_2 = (U[:, 0:range_2]).dot(np.diag(sigma[0:range_2])).dot(VT[0:range_2, :])
 
fig, ax = plt.subplots(1, 3, figsize=(24, 8))
 
ax[0].imshow(img)
ax[0].set(title="src")
ax[1].imshow(img_1.astype(np.uint8))
ax[1].set(title="nums of sigma = 6")
ax[2].imshow(img_2.astype(np.uint8))
ax[2].set(title="nums of sigma = 120")
plt.show()

2.5.协同过滤推荐系统中矩阵分解应用

SVD 全程奇异值分解，原本是是线性代数中的一个知识，在推荐算法中用到的 SVD 并非正统的奇异值分解。前面已经知道通过矩阵分解，可以得到用户矩阵和物品矩阵。针对每个用户和物品，假设分解后得到的用户 u 的向量为 p_u，物品 i 的向量为 q_i，那么用户 u 对物品 i 的评分为：

 

其中，K 表示隐因子个数。为给每个用户和物品生成k维向量，首先需将该问题转化成机器学习问题，要解决机器学习问题，就需要寻找损失函数以及优化算法。这里单个用户对单个物品的真实评分与预测评分之间的差值记为 e{ui}。

其中，R 表示所有的用户对所有物品的评分集合，K 表示隐因子个数。我们要做的就是求出用户向量 p_u 和物品向量 q_i ，来保证损失函数结果最小。求解损失函数优化算法常用的选择有两个，一个是梯度下降（GD），另一个是交替最小二乘（ALS） 。这里以梯度下降为例。

1. 准备好用户物品的评分矩阵，每一条评分数据看做一条训练样本；
2. 给分解后的 P 矩阵和 Q 矩阵随机初始化元素值；
3. 用 P 和 Q 计算预测后的分数；
4. 计算预测的分数和实际的分数误差；
5. 沿着损失函数梯度下降的方向更新 P 和 Q 中的元素值；
6. 重复步骤 3 到 5，直到达到停止条件。

梯度下降算法的一个关键点在于计算损失函数对于每个参数的梯度。

 

3.SVD++

3.1. 增加偏执项的SVD

在实际应用中，会存在以下情况：相比于其他用户，有些用户给分就是偏高或偏低。相比于其他物品，有些物品就是能得到偏高的评分。所以使用 pu*qi^T 来定义评分是有失偏颇的。我们可以认为 评分 = 兴趣 + 偏见。其中，μ表示全局均值， bu表示用户偏见，bi表示物品偏见。

而上式中的相关参数同样也可通过机器学习优化算法的相关方式获得。

 

3.2.SVD++

实际生产中，用户评分数据很稀少，也就是说显式数据比隐式数据少很多，SVD++ 就是在 SVD 模型中融入用户对物品的隐式行为。我们可以认为 评分=显式兴趣 + 隐式兴趣 + 偏见。那么隐式兴趣如何加入到模型中呢？首先，隐式兴趣对应的向量也是 k 维，它由用户有过评分的物品生成，因为，评分的行为从侧面反映了用户的喜好，可以将这样的反映通过隐式参数的形式体现在模型中：

 

其中 I(u) 为该用户所评价过的所有电影的集合，yj为隐藏的“评价了电影 j”反映出的个人喜好偏置。收缩因子取集合大小的根号是一个经验公式，并没有理论依据。模型参数bi,bu,qi,pu,yj通过最优化下面这个目标函数获得：