Python机器学习--分类算法--朴素贝叶斯算法_python 朴素贝叶斯算法

朴素贝叶斯算法

朴素贝叶斯算法类型

朴素贝叶斯算法属于有监督学习中的分类算法，基于贝叶斯理论和特征相互独立的假设，因为假设特征相互独立让问题变得简单，因此称为朴素.

朴素贝叶斯算法分为:伯努利朴素贝叶斯,高斯朴素贝叶斯,多项式朴素贝叶斯,因此此篇,篇幅较长,需要看某一个算法,可以使用ctrl+F进行搜索即可.

朴素贝叶斯算法第一站:概率公式

条件概率公式为(即在事件B发生的情况下,事件A发生的概率):

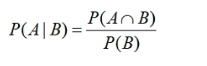
当A,B相互独立时 P(AB) = P(A)∗P(B)

全概率公式:

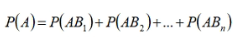
贝叶斯公式:

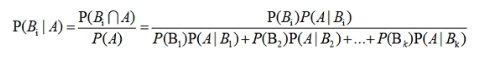
朴素贝叶斯算法第二站:朴素贝叶斯计算步骤

1.一个数据集中有两个样本(B1，B2， B3)、(C1，C2，C3)和一个标签的两组(A1，A2)
2.给定一个测试样本(D1，D2，D3)，使用贝叶斯公式求出测试样本属于A1组还是A2组


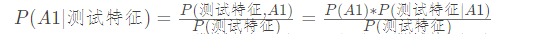
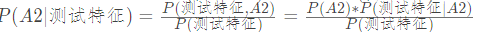
3.由于两式分母都是相同的，所以只需要考虑分子就可以了

4.这时遇到一个问题，如果所选特征在训练集中不存在P(测 试特征∣A1) 将会等于0，最终的概率也会等于0，显然这样的结果不是我们想要的

5.这就需要我们引入特征相互独立的假设了

6.根据在训练集数据就可以计算出A1的概率以及A1的条件下D1、D2、D3发生的概率了

7.虽然是能计算出来，但是可能会出现D1这个特征没有出现在训练集特征的情况，比如D1=高，恰好A1组相应类型特征对应的数据低，它的概率也会变成0

8.这是就出现了一个拉普拉斯系数，当测试集特征不存在(为0次)时，给它变成1，相应的分母也要加一。例如，测试集某个特征不存在，概率本应该是 $\frac{0}{n}$ ，使用拉普拉斯系数后就变成了$\frac{1}{n+1}$，一旦有一个是找不到的，所有测试集特征都要分子分母各加一.

基于sklearn实现伯努利贝叶斯

伯努利贝叶斯简介

伯努利分布又称0-1分布，也叫二项分布，所以伯努利朴素贝叶斯只能对符合二分类数据的特征
伯努利分布公式：

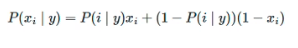
和上面朴素贝叶斯计算步骤有所不同的是，拉普拉斯系数不同。伯努利中的拉普拉斯，分母计算方法是符合计算标签结果的特征条数加上标签类别数，分子还是加1。比如，标签是下雨和没雨，现在判断的是下雨的条件下特征发生的概率，符合条件的训练集特征有4条，分母就是4+2=6。

何种情况使用伯努利朴素贝叶斯

伯努利分布:比如正面或反面，成功或失败，有缺陷或没有缺陷，病人康复或未康复。为方便起见，记这两个可能的结果为0和1.

适用于特征和标签呈现伯努利分布时使用，也适用于文本数据（此时特征表示的是是否出现，例如某个词语的出现为1，不出现为0）

绝大多数情况下表现不如多项式分布，但有的时候伯努利分布表现得要比多项式分布要好，尤其是对于小数量级的文本数据

sklearn中代码实现

from sklearn.naive_bayes import BernoulliNB
# 实例化
alg = BernoulliNB()
# 参数：alpha，默认是等于拉普拉斯，防止等于零的情况出现

# 拟合  X_train,y_train为提前切分好的测试数据的特征和标签
alg.fit(X_train, y_train)

# 预测结果
y_pred = alg.predict(X_test)
print('预测结果：', y_pred)

# 预测概率
print('预测概率：', alg.predict_proba(X_test))

# 查看准确率
score = alg.score(X_test, y_test)
print('准确率：', score)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

基于sklearn实现高斯朴素贝叶斯

高斯贝叶斯简介

高斯朴素贝叶斯主要是用来处理连续数据类型的特征
概率密度函数(μ代表均值，σ代表标准差):

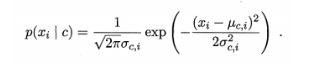
何种情况使用高斯朴素贝叶斯

当数据的特征呈现为高斯分布进行分类时使用(生活中绝大部分数据)

sklearn中代码实现

from sklearn.naive_bayes import GaussianNB
# 实例化
alg = GaussianNB()
# 参数：alpha，默认是等于拉普拉斯，防止等于零的情况出现

# 拟合
alg.fit(X_train, y_train)

# 预测结果
y_pred = alg.predict(X_test)
print('预测结果：', y_pred)

# 预测概率
print('预测概率：', alg.predict_proba(X_test))

# 查看准确率
score = alg.score(X_test, y_test)
print('准确率：', score)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

基于sklearn实现多项式朴素贝叶斯

多项式朴素贝叶斯简介

多项式朴素贝叶斯多用于出现次数作为特征的数据，特征数据值必须是非负的。对于文本数据的处理，就非常适合用多项式朴素贝叶斯.

多项式朴素贝叶斯计算原理:

• 比如有一个预测好坏评论的数据集，在第一个样本中good出现了2次，bad出现了0次，是好评；在第二个样本中good出现了0次，bad出现了2次，是差评。

• 现在有一测试集 [ 5，0 ]

• 利用朴素贝叶斯公式分别计算 P ( 好 评 ∣ 特 征 ) 和P ( 差 评 ∣ 特 征 )

• 真实结果为好评和差评的都有0，所以需要考虑拉普拉斯，分母等于此类别下特征条数+类别数,分子加1.
  
  需要在概率上增加测试集对应特征出现次数次方
  

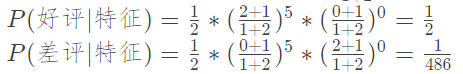
• 所以最终得出结论，[ 5, 0 ]的测试结果是好评

何时使用多项式朴素贝叶斯算法

1.适用于文本数据（特征表示的是次数，例如某个词语的出现次数
2.适用于特征为连续数据类型的.

sklearn中代码实现

from sklearn.naive_bayes import MultionmialNB
# 实例化
alg = MultionmialNB()
# 拟合
alg.fit(X_train, y_train)

# 查看预测结果
y_pred = alg.predict(X_test)
print('预测结果：', y_pred)

# 查看预测概率
print('概率：', alg.predict_proba(X_test))
1
2
3
4
5
6
7
8
9
10
11
12

使用多项式朴素贝叶斯进行文本词频统计

以评论数据为例
1.使用jieba库,并定义切分汉语词汇的函数

import jieba  # 结巴分词
from sklearn.navie_state import MultionmialNB


# ------------------------------分词处理----------------------------
def get_word(val):
	return ' '.join(list(jieba.cut(val)))
X = X.transform(get_word)
1
2
3
4
5
6
7
8

2.词频向量化
词频向量化，是对分词后的数据进行统计样本中出现的次数，分为普通词频向量化和 TF-IDF词频向量化

普通词频向量化是统计出现次数，下面是普通词频向量化的代码实现

from sklearn.feature_extraction.text import CountVectorizer
# 实例化
cv = CountVectorizer()
# 参数：stop_words：停用词，通常是读取一个停用词文本文件作为停用词词典

# 查看处理后的数据词典
print('词典：', cv.get_feature_names())
# 查看词典字典，词作为键，对应词典的索引作为值
print('词典字典：', cv.vocabulary_)

# 拟合，一般都是在训练集上拟合
cv.fit(X_train) 
# 向量化处理
X_train = cv.transform(X_train).toarray()
X_test = cv.transform(X_test).toarray()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

TF-IDF词频向量化
词频：TF，指的是某一个给定的词语在该文件中出现的频率
逆向文件频率：IDF，是一个词语普遍重要性的度量

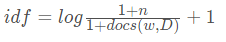
TF-IDF = TF*IDF

TF-IDF词频向量化是统计的词的重要性，下面是代码实现

from sklearn.feature_extraction.text import TfidfVectorizer
# 实例化
tv = TfidfVectorizer()

# 拟合，一般都是在训练集上拟合
tv.fit(X_train) 
# 向量化处理
X_train = tv.transform(X_train).toarray()
X_test = tv.transform(X_test).toarray()

"""
TF-IDF返回的结果是概率的形式
如果一个词在当前语句中出现了多次，在其他语句中出现的次数少------重要的词
如果一个词在当前语句中出现了多次，在其他语句中出现的次数也多------重要的词
"""
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

TD-IDF的计算方法:

1.TF=这个词在该条语句中出现的次数
2.套用 idf 计算公式

3.计算出TF*IDF的值，比如该条语句中有三个在词典中出现的词，他们对应的TF-IDF为a、b、c

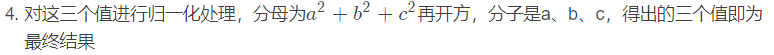
增量学习

增量学习：不断增加数据进行学习，分批加入训练样本进行训练，大多数情况下是数据量太大，需要分批训练时使用
只有朴素贝叶斯可以进行增量学习

sklearn实现

import joblib
from sklearn.naive_bayes import GaussianNB  # 例如使用高斯朴素贝叶斯
# ----------拆分数据集----------------
# ----------划分出若干组数据-----------
X_train1, y_train1
X_train2, y_train2

# ---------使用算法-------------------
# 实例化
alg = GaussianNB()
# 这里就使用部分拟合，第一次使用部分拟合需要加classes
alg.partial_fit(X_train1, y_train1, classes=[0, 1])
# 参数：X_train, y_train, classes：标签去重后的值

# -----------保存模型-----------------
joblib.dump(算法名称, '文件名.model')

# 将第一拟合和保存模型注释掉，再来读取模型进行拟合
alg = joblib.load('文件名.model')
alg.partial_fit(X_train2, y_train2)
print('查看准确率：', alg.score(X_test, y_test))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

朴素贝叶斯算法总结

1.计算速度快【原因：假定特征相互独立】
2.少量数据仍然可以进行训练，使用较小数据集
3.特征不需要标准化
4.可以进行增量学习