搭建机器人电控系统——滤波算法——数据处理的十种滤波算法_数据处理滤波

滤波算法

我们需要精确的数据，但是数据回传并不完全准确时，比如十个数据里面有一个不正常时，我们就需要做滤波处理。不同滤波算法要结合实际情况来考虑，甚至有些时候需要自己写一个完全不同的以适应你的数据特征。以下介绍十种滤波的方法。

---

限幅滤波

方法：确定数据偏差的最大值MAX；求每次采样数据与上一次数据之差，若<=MAX则有效，若无效，则用上一次数据代替此次数据。
代码：

1./* MAX值根据实际调，Value有效值，new_Value当前采样值，程序返回有效的实际值 */  
2.#define A 10  
3.char Value;  
4.char filter()  
5.{  
6.  char new_Value;  
7.  new_Value = get_ad();                             //获取采样值  
8.  if( abs(new_Value - Value) > MAX)   return Value;   //abs()取绝对值函数  
9.  return new_Value;  
10.}  
1
2
3
4
5
6
7
8
9
10

适用：有脉冲干扰的情形，无法抑制周期性干扰，平滑度差。

---

限幅平均滤波

方法：每次通过的数据先限幅滤波后再使用；取平均值。
代码：

1.#define MAX 10  
2.#define N 12 //总数量  
3.char value,i=0;  
4.char value_buf[N];  
5.char filter()  
6.{  
7. char new_value,sum=0;  
8. new_value=get_ad();  
9. if(Abs(new_value-value)<MAX)  
10.  value_buf[i++]=new_value;  
11. if(i==N)i=0;  
12. for(count =0 ;count<N;count++)  
13.  sum+=value_buf[count];  
14. return (char)(sum/N);  
15.}  
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

适用：消除脉冲干扰，随机干扰，占用RAM资源较多。

---

中位值滤波

方法：连续采样N次，按大小排列；取中间值。
代码：

1.#define N 11  
2.char filter()  
3.{  
4. char value_buf[N];  
5. char count,i,j,temp;  
6. for(count = 0;count < N;count++)         //获取采样值  
7. {  
8.  value_buf[count] = get_ad();  
9.  delay();  
10. }  
11. for(j = 0;j<(N-1);j++)  
12.  for(i = 0;i<(n-j);i++)  
13.  if(value_buf[i]>value_buf[i+1])  
14.  {  
15.   temp = value_buf[i];  
16.   value_buf[i] = value_buf[i+1];  
17.   value_buf[i+1] = temp;  
18.  }  
19. return value_buf[(N-1)/2];  
20.}  
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

适用：克服波动干扰，对变化缓慢的参数比较良好，不适用于速度变化快的参数。

---

中位值平均滤波

方法：采样N个值，去掉最大最小，计算平均值。
代码：

1.char filter()  
2.{  
3. char count,i,j;  
4. char Value_buf[N];  
5. int sum=0;  
6. for(count=0;count<N;count++)  
7.  Value_buf[count]= get_ad();  
8. for(j=0;j<(N-1);j++)  
9.  for(i=0;i<(N-j);i++)  
10.   if(Value_buf[i]>Value_buf[i+1])  
11.   {  
12.     temp = Value_buf[i];  
13.     Value_buf[i]= Value_buf[i+1];  
14.      Value_buf[i+1]=temp;  
15.   }  
16.   for(count =1;count<N-1;count++)  
17.    sum += Value_buf[count];  
18.   return (char)(sum/(N-2));  
19.} 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

适用：克服波动干扰（中位），随机误差（平均），脉冲干扰（限幅）。占用RAM资源较多。

---

算术平均滤波

方法：连续采样取平均值。
代码：

1.#define N 12  
2.char filter()  
3.{  
4. int sum = 0;  
5. for(count = 0;count<N;count++)  
6.  sum += get_ad();  
7. return (char)(sum/N);  
8.}  
1
2
3
4
5
6
7
8

适用：采样数量较大时平滑度高、灵敏度低；数量少时平滑度低、灵敏度高。适用于存在随机干扰的情况，占用RAM资源较多。

---

递推平均滤波

方法：取N个值，形成队列，先进先出，取平均值。
适用：随机干扰的系统，占用RAM较多。

---

加权平均递推滤波

方法：对不同时刻采样的数据加以不同的权重，如越新的数据权重越大，这样灵敏度比较高，但平滑度低。
代码：

1./* coe数组为加权系数表 */  
2.#define N 12  
3.char code coe[N]={1,2,3,4,5,6,7,8,9,10,11,12};  
4.char code sum_coe={1+2+3+4+5+6+7+8+9+10+11+12};  
5.char filter()  
6.{  
7. char count;  
8. char value_buf[N];  
9. int sum=0;  
10. for(count=0;count<N;count++)  
11. {  
12.  value_buf[count]=get_ad();  
13. }  
14. for(count=0;count<N;count++)  
15.  sum+=value_buf[count]*coe[count];  
16. return (char)(sum/sum_coe);  
17.}  
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

适用：如果以后进数据权重较大，那么适用于滞后系统、采样周期短系统，对变化慢的信号不能迅速反应。

---

一阶滞后滤波（低通滤波）

方法：在本次采样数据和上次数据之间分配不同的信任度（信任度从0到1），也可以是观测数据和你理论计算数据之间分配不同的信任度。
代码：

1./*为加快程序处理速度，取a=0~100*/  
2.#define a 30  
3.char value;  
4.char filter()  
5.{  
6. char new_value;  
7. new_value=get_ad();  
8. return ((100-a)*value + a*new_value);  
9.}  
1
2
3
4
5
6
7
8
9

适用：适用于干扰频率较高的场合，但灵敏度低，相位滞后。

---

限幅消抖滤波

方法：对采样的数据先进行限幅。将采样值和当前值比较，若采样值=当前值，则计数器清零，若采样值不等于当前值，则计数器加一。最终若计数器溢出，则用采样值替换当前值，计数器清零。
代码：

1.#define MAX 10  
2.#define N 12  
3.char value;  
4.char filter()  
5.{  
6. char new_value,count=0;  
7. new_value=get_ad();  
8. while(value!=new_value)  
9. {  
10.  if(Abs(value-new_value)<MAX)  
11.  {  
12.  count++;  
13.  if(count>=N) return new_value;  
14.  new_value=get_ad();  
15.  }  
16. return value;  
17. }  
18.}  
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

适用：适用于变化慢的数据，不适用于变化快的数据，避免脉冲干扰（限幅）。

---

卡尔曼滤波

适用系统：线性高斯系统（将噪声的分布看成正态分布）。
方法：在理论计算值和观测值之间分配信任度（信任度A从0到1）。用上一次的最优结果得到理论计算的当前值，同时使用观测值修正当前值，得到最优结果。

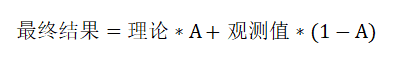
我们把用上一次的最优结果得到理论计算的当前值的过程用状态方程来表示：

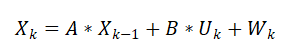
其中Wk为状态方程噪声（如环境的随机干扰，场面粗糙程度等），满足正态分布：

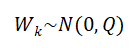
我们把使用观测值修正当前值的过程用观测方程来表示：

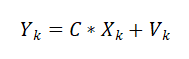
其中Vk为观测方程噪声（传感器返回的噪声），满足正态分布：

卡尔曼滤波的思路就是调整Q和R的参数值（和PID类似），从而让最终结果变得很好。