PyTorch | 激活函数（Sigmoid、Tanh、ReLU和Leaky ReLU）_leaky rectified linear unit

1. 简介

\qquad 在深度学习中，输入值和矩阵的运算是线性的，而多个线性函数的组合仍然是线性函数，对于多个隐藏层的神经网络，如果每一层都是线性函数，那么这些层在做的就只是进行线性计算，最终效果和一个隐藏层相当！那这样的模型的表达能力就非常有限 。
\qquad 实际上大多数情况下输入数据和输出数据的关系都是非线性的。所以我们通常会用非线性函数对每一层进行激活，大大增加模型可以表达的内容（模型的表达效率和层数有关）。

\qquad 这时就需要在每一层的后面加上激活函数，为模型提供非线性，使得模型可以表达的形式更多，同时也可以更改模型的输出值，使模型可以实现回归或者分类的功能。激活函数是连续的（continuous），且可导的（differential）。常见的激活函数有Sigmoid、Tanh、ReLU和Leaky ReLU。下面分别对其进行介绍。

2. 函数饱和性

假设 $f(x)$ 是一个激活函数。

• $右饱和$：
  \qquad 当 $x$ 趋向于正无穷时，激活函数的导数趋近于 $0$，此时称为右饱和激活函数。$\underset{x\to +\infty }{\lim }{f}^{\prime }(x)=0$
• $左饱和$：
  \qquad 当 $x$ 趋向于负无穷时，激活函数的导数趋近于 $0$，此时称为左饱和激活函数。$\underset{x\to -\infty }{\lim }{f}^{\prime }(x)=0$
• $饱和函数$：
  \qquad 当一个函数既满足右饱和，又满足左饱和，则称为饱和激活函数，否则称为非饱和激活函数。
• $硬饱和$：
  \qquad 对于任意的 $x$，如果存在常数 $c$，当 $x>c$ 时，恒有 $f^{\prime }(x)=0$，则称其为右硬饱和。如果对于任意的 $x$，如果存在常数 $c$，当 $x<c$ 时，恒有 $f^{\prime }(x)=0$，则称其为左硬饱和。既满足左硬饱和又满足右硬饱和的函数称之为硬饱和函数。
• $软饱和$：
  \qquad 对于任意的 $x$，如果存在常数 $c$，当 $x>c$ 时，恒有 $f^{\prime }(x)$ 趋近于$0$，则称其为右软饱和。如果对于任意的 $x$，如果存在常数 $c$，当 $x<c$ 时，恒有 $f^{\prime }(x)$ 趋近于 $0$，则称其为左软饱和。既满足左软饱和又满足右软饱和的函数称之为软饱和函数。
• $常用的饱和激活函数和非饱和激活函数$：
  \qquad 饱和激活函数有如 $Sigmoid$ 和 $Tanh$，非饱和激活函数有 $ReLU$；相较于饱和激活函数，非饱和激活函数可以解决“梯度消失（梯度弥散）”的问题，加快收敛。

3. 以零为中心

3.1 收敛速度

\qquad 首先，我们需要给收敛速度做一个诠释。模型的最优解即是模型参数的最优解。通过逐轮迭代，模型参数会被更新到接近其最优解。这一过程中，迭代轮次多，则我们说模型收敛速度慢；反之，迭代轮次少，则我们说模型收敛速度快。

3.2 参数更新

\qquad 深度学习一般的学习方法是反向传播。简单来说，就是通过链式法则，求解全局损失函数 $L(\vec{x})$ 对某一参数 $w$ 的偏导数（梯度）；然后辅以学习率 $\eta$，向梯度的反方向更新参数 $w$：$w-\eta \cdot \frac{\partial L}{\partial w}\to w$。
\qquad 考虑学习率 $\eta$ 是全局设置的超参数，参数更新的核心步骤即是计算 $\frac{\partial L}{\partial w}$。再考虑到对于某个神经元来说，其输入与输出的关系是 $f(\vec{x};\vec{w},\vec{b})=f(z)=f(\sum _i{w}_i{x}_i+b)$。
\qquad 因此，对于参数 $w_i$ 来说，$\frac{\partial L}{\partial w_i}=\frac{\partial L}{\partial f}\cdot \frac{\partial f}{\partial z}\cdot \frac{\partial z}{\partial w_i}=x_i\cdot \frac{\partial L}{\partial f}\cdot \frac{\partial f}{\partial z}$，参数的更新步骤变为 $w_i-\eta \cdot x_i\cdot \frac{\partial L}{\partial f}\cdot \frac{\partial f}{\partial z}\to w_i$。

3.3 更新方向

\qquad 由于 $w_i$ 是上一轮迭代的结果，此处可视为常数，而 $\eta$ 是模型超参数，参数 $w_i$ 的更新方向实际上由 $x_i\cdot \frac{\partial L}{\partial f}\cdot \frac{\partial f}{\partial z}$ 决定。又考虑到 $\frac{\partial L}{\partial f}\cdot \frac{\partial f}{\partial z}$ 对于所有的 $w_i$ 来说是常数，因此各个 $w_i$ 更新方向之间的差异，完全由对应的输入值 $x_i$ 的符号决定。

3.4 以零为中心的影响

\qquad 至此，为了描述方便，我们以二维的情况为例。亦即，神经元描述为 $f(\vec{x};\vec{w},\vec{b})=f(w_0{x}_0+w_1{x}_1+b)$。现在假设，参数 $w_0，w_1$ 的最优解 $w_0^{\ast }，w_1^{\ast }$ 满足条件
{ w 0 < w 0 ∗ w 1 ≥ w 1 ∗ \left\{

$$\begin{aligned} w_0<w_0^*\\w_1\geq w_1^* \end{aligned}$$ \right. {w0​<w0∗​w1​≥w1∗​​
这也就是说，我们希望 $w_0$ 适当增大，但希望 $w_1$ 适当减小，这就必然要求 $x_0$ 和 $x_1$ 符号相反。但在 $Sigmoid$ 函数中，输出值恒为正，这也就是说，如果上一级神经元采用 $Sigmoid$ 函数作为激活函数，那么我们无法做到 $x_0$ 和 $x_1$ 符号相反。

\qquad 如图所示，模型参数走绿色箭头能够最快收敛，但由于 $w_0$ 和 $w_1$ 的符号总是相同，所以模型参数可能走类似红色折线的箭头。如此一来，使用 $Sigmoid$ 函数作为激活函数的神经网络，收敛速度就会慢上很多。

4. Sigmoid（S 型生长曲线）

$Sigmoid$ 函数是一个在生物学中常见的 $S$ 型函数，也称为 $S$ 型生长曲线，$Sigmoid$ 函数也叫 $Logistic$ 函数。$Sigmoid$ 函数连续，光滑，严格单调。在信息科学中，由于其单增以及反函数单增等性质，$Sigmoid$ 函数常被用作神经网络的激活函数，将变量映射到 $[0,1]$ 之间，一般用来做二分类。$Sigmoid$ 函数在统计学和机器学习领域应用最为广泛的是逻辑回归模型。$Sigmoid$ 的函数表达式如下：
$$S(x)=\frac{1}{1+e^{-x}}=\frac{e^x}{e^x+1}$$
\qquad 该函数具有如下的特性：当 $x$ 趋近于负无穷时，$y$ 趋近于 $0$；当 $x$ 趋近于正无穷时，$y$ 趋近于 $1$；当 $x=0$ 时，$y=0.5$。
$Sigmoid$ 函数的导数是其本身的函数：
$S^{\prime }(x)=\frac{-1}{(1+e^{-x}{)}^2}\cdot (0+(-1)\cdot e^{-x}))=\frac{e^{-x}}{(1+e^{-x}{)}^2}=\frac{e^{-x}}{1+e^{-x}}\cdot \frac{1}{1+e^{-x}}$
$=\frac{1+e^{-x}-1}{1+e^{-x}}\cdot \frac{1}{1+e^{-x}}=(1-\frac{1}{1+e^{-x}})\cdot \frac{1}{1+e^{-x}}=(1-S(x))\cdot S(x)$
\qquad 函数 $S(x)$（蓝色）和导数 $S^{\prime }(x)$（黄色）对应的曲线为：

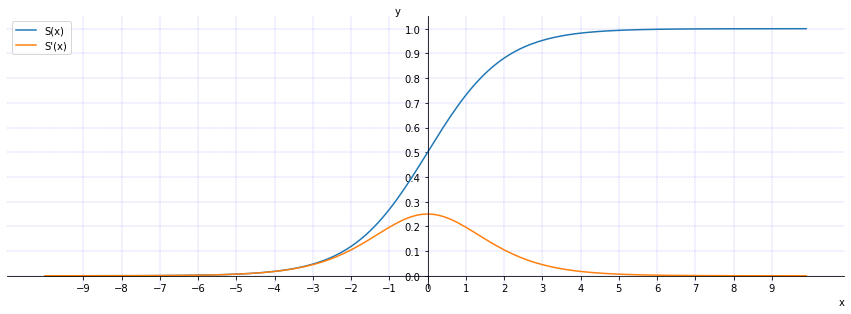
\qquad 由于在反向传递过程中，$Sigmoid$ 向下传导的梯度包含了一个 $f^{\prime }(x)$ 因子（$Sigmoid$ 关于输入的导数），因此一旦输入落入饱和区，$f^{\prime }(x)$ 就会变得接近于 $0$，权重基本不会更新，导致了向底层传递的梯度也变得非常小。此时，网络参数很难得到有效训练。这种现象被称为梯度消失（梯度弥散）。此外，$Sigmoid$ 函数的输出均大于 $0$，使得输出不是 $0$ 均值，这称为偏移现象（偏移现象会影响网络的收敛性），这会导致后一层的神经元将得到上一层输出的非 $0$ 均值的信号作为输入。最后，$Sigmoid$ 计算复杂度高，因为 $Sigmoid$ 函数是 $exp$ 指数形式。

import torch
import matplotlib.pyplot as plt 

# sigmoid 函数图像
x = torch.arange(-10,10,0.1)
y = torch.sigmoid(x)

# sigmoid 导数图像
dev_y = y*(1-y)

plt.figure()
plt.xlabel('x',loc='right')
plt.ylabel('y',loc='top',rotation=0)

# Get current axis 获得整张图表的坐标对象
ax = plt.gca()

# 隐藏右侧与上面两条边
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')

ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')

# 指定 x轴 和 y轴 的绑定
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))

plt.grid(color='b', linewidth='0.15' ,linestyle='-.')
plt.plot(x, y)
plt.plot(x,dev_y)
plt.xticks(torch.arange(-9,10,1))
plt.yticks(torch.arange(0,1.1,0.1))
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

5. Tanh（双曲正切函数）

$Tanh$ 激活函数是 $Sigmoid$ 的不同形式，两者类似，与 $Sigmoid$ 相比，它的输出均值是 $0$，输出值范围由 $(0,1)$ 变为了 $(-1,1)$，使得其收敛速度要比 $Sigmoid$ 快，减少迭代次数，可以把 $Tanh$ 函数看做是 $sigmoid$ 向下平移和拉伸后的结果。$Tanh$ 的归一化范围为 $-1$ 到 $1$，解决 $Sigmoid$ 非零取值的缺点。（一般在二分类问题中，隐藏层使用 $Tanh$ 函数，输出层使用 $Sigmoid$ 函数，但是随着 $ReLU$ 的出现所有的隐藏层基本上都使用 $ReLU$ 来作为激活函数了）。$Tanh$ 对应的函数表达式：
$$T(x)=\frac{sinh(x)}{cosh(x)}=\frac{\frac{e^x-e^{-x}}{2}}{\frac{e^x+e^{-x}}{2}}=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$
$Tanh$ 函数和 $Sigmoid$ 函数 $S(x)=\frac{1}{1+e^{-x}}$ 的关系如下：
$$\begin{gathered} T(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}=\frac{1-e^{-2x}}{1+e^{-2x}}=\frac{2}{1+e^{-2x}}-1=2S(2x)-1 \\ （Sigmoid图像向下平移1个单位） \\ （Sigmoid图像水平拉伸到原来的2倍(2x)） \\ （Sigmoid图像垂直拉伸到原来的2倍） \end{gathered}$$
$Tanh$ 函数对应的导数：
$T^{\prime }(x)=(\frac{e^x-e^{-x}}{e^x+e^{-x}}{)}^{\prime }=\frac{(e^x-e^{-x}{)}^{\prime }(e^x+e^{-x})-(e^x-e^{-x})(e^x+e^{-x}{)}^{\prime }}{(e^x+e^{-x}{)}^2}$
$=\frac{(e^x+e^{-x}{)}^2-(e^x-e^{-x}{)}^2}{(e^x+e^{-x}{)}^2}=1-(\frac{e^x-e^{-x}}{e^x+e^{-x}}{)}^2=1-T^2(x)$
\qquad 函数 $T(x)$（蓝色）和导数 $T^{\prime }(x)$（黄色）对应的曲线为：

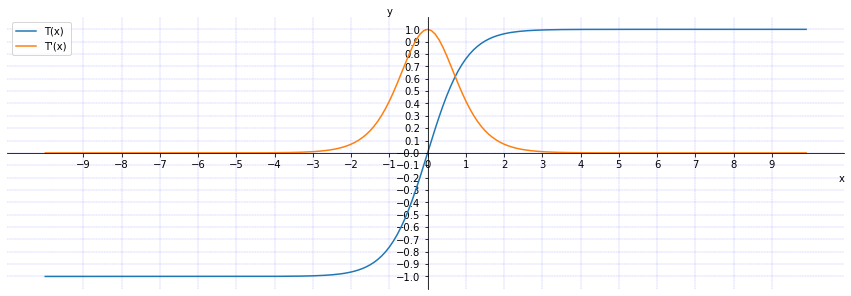
\qquad 从上图中可以看出 $Sigmoid$ 和 $Tanh$ 有相同的缺点，在值非常大的时候，函数的导数会变得特别小（由两者的函数曲线可知），甚至接近于 $0$，使得梯度下降的速度减缓，导致模型学习的效率降低，即梯度消失，在多层线性网络中，情况更严重。
\qquad 在隐藏层中使用 $Tanh$ 函数的效果总体上是优于 $Sigmoid$ 函数的。 因为函数值域在 $-1$ 到 $+1$ 之间的激活函数，它的输出是以零为中心的，因此实际应用中 $Tanh$ 会比 $Sigmoid$ 更好，但是仍然存在梯度饱和与 $exp$ 计算复杂度高的问题。在训练一个算法模型时，如果使用 $Tanh$ 函数代替 $Sigmoid$ 函数，就会使得输出数据的平均值更接近 $0$（$Tanh$ 函数能起到归一化（均值为 $0$）的效果）而不是 $0.5$。即输入为负数的话，输出也为负数；同理输入为正数，输出也为正数。

import torch
import matplotlib.pyplot as plt 

# sigmoid 函数图像
x = torch.arange(-10,10,0.1)
y = torch.tanh(x)

# sigmoid 导数图像
dev_y = 1-torch.square(y)

plt.figure(figsize=(15,5))
plt.xlabel('x',loc='right')
plt.ylabel('y',loc='top',rotation=0)

# Get current axis 获得整张图表的坐标对象
ax = plt.gca()

# 隐藏右侧与上面两条边
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')

ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')

# 指定 x轴 和 y轴 的绑定
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))

plt.grid(color='b', linewidth='0.15' ,linestyle='-.')
plt.xticks(torch.arange(-9,10,1))
plt.yticks(torch.arange(-3,1.1,0.1))
l1, = plt.plot(x, y)
l2, = plt.plot(x,dev_y)
plt.legend(handles=[l1,l2],labels=['T(x)','T\'(x)'],loc='best')
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

6. ReLU（Rectified Linear Unit，整流线性单元函数）

$ReLU$ 函数是深度学习中较为流行的一种激活函数，$ReLU$ 函数是一个分段的函数，计算公式为：
R ( x ) = { x i f   x ≥ 0 0 i f   x < 0 R(x)=\left\{

$$\begin{aligned} x\qquad if\ x\geq 0 \\0\qquad if\ x<0 \end{aligned}$$ \right. R(x)={xif x≥00if x<0​
$ReLU$ 函数对应的导数：
$$R^{\prime }(x)=\{\begin{array}{r}1ifx\ge 0\\ 0ifx<0\end{array}$$
\qquad 函数 $R(x)$（蓝色）和导数 $R^{\prime }(x)$（黄色）对应的曲线为：

\qquad 从图中可以看出对于所有为正值的输入，其梯度都为 $1$，不存在饱和问题；对于小于 $0$ 的数据，梯度都为 $0$，$ReLU$ 硬饱和。所以，$ReLU$ 能够在 $x>0$ 时保持梯度不衰减，从而缓解梯度消失问题。
$ReLU$ 有一个问题就是所有负值输入后都立即变为零，这降低了模型根据数据进行适当拟合或训练的能力。这意味着任何给 $ReLU$ 激活函数的负输入都会立即把值变成零。随着训练的推进，部分输入会落入硬饱和区，导致对应权重无法更新，这种现象被称为“Dead ReLU（神经元坏死现象）”。同时，与 $Sigmoid$ 类似，$ReLU$ 的输出均值也大于 $0$，偏移现象和神经元坏死会共同影响网络的收敛性。

import torch
import matplotlib.pyplot as plt 

# relu 函数图像
x = torch.arange(-5,5,0.1)
y = torch.relu(x)

# relu 导数图像
dev_y = torch.ge(x,0)

plt.figure(figsize=(15,5))
plt.xlabel('x',loc='right')
plt.ylabel('y',loc='top',rotation=0)

# Get current axis 获得整张图表的坐标对象
ax = plt.gca()

# 隐藏右侧与上面两条边
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')

ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')

# 指定 x轴 和 y轴 的绑定
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))

plt.grid(color='b', linewidth='0.15' ,linestyle='-.')
plt.xticks(torch.arange(-5,6,1))
plt.yticks(torch.arange(-1,6,1))
l1, = plt.plot(x, y)
l2, = plt.plot(x,dev_y)
plt.legend(handles=[l1,l2],labels=['R(x)','R\'(x)'],loc='best')
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

7. Leaky ReLU（Leaky Rectified Linear Unit，渗漏整流线性单元函数）

$LeakyReLU$ 函数是 $ReLU$ 函数的一种变形，它是一种专门设计用于解决 $DeadReLU$ 问题的激活函数。函数使用一个类似 $0.01$ 的小值来初始化神经元，从而使得 $ReLU$ 在负数区域更偏向于激活而不是死掉。函数表达式为：
L ( x ) = { x i f   x ≥ 0 λ x i f   x < 0 其 中   λ   为   ( 0 , 1 )   范 围 内 的 数 。 L(x)=\left\{

$$\begin{aligned} x\qquad if\ x\geq 0 \\\lambda x\qquad if\ x<0 \end{aligned}$$ \right.\qquad 其中\ \lambda\ 为\ (0,1)\ 范围内的数。 L(x)={xif x≥0λxif x<0​其中 λ 为 (0,1) 范围内的数。
$LeakyReLU$ 函数对应的导数：
$$L^{\prime }(x)=\{\begin{array}{r}1ifx\ge 0\\ \lambda ifx<0\end{array}其中\lambda 为(0,1)范围内的数。$$
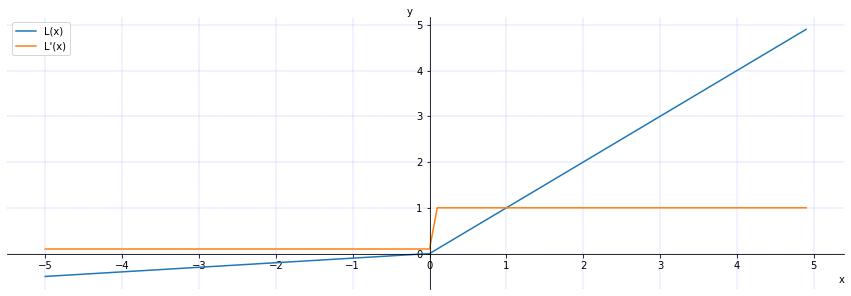
\qquad 函数 $L(x)$（蓝色）和导数 $L^{\prime }(x)$（黄色）对应的曲线为：

import torch
import matplotlib.pyplot as plt 

# relu 函数图像
x = torch.arange(-5,5,0.1)
a = torch.tensor(0.1)
l = torch.nn.LeakyReLU(a)
y = l(x)

# relu 导数图像
dev_y = torch.ge(x,0).float()
dev_y = torch.where(dev_y == 0, a, dev_y)
dev_y

plt.figure(figsize=(15,5))
plt.xlabel('x',loc='right')
plt.ylabel('y',loc='top',rotation=0)

# Get current axis 获得整张图表的坐标对象
ax = plt.gca()

# 隐藏右侧与上面两条边
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')

ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')

# 指定 x轴 和 y轴 的绑定
ax.spines['bottom'].set_position(('data', 0))
ax.spines['left'].set_position(('data', 0))

plt.grid(color='b', linewidth='0.15' ,linestyle='-.')
plt.xticks(torch.arange(-5,6,1))
plt.yticks(torch.arange(-1,6,1))
l1, = plt.plot(x, y)
l2, = plt.plot(x,dev_y)
plt.legend(handles=[l1,l2],labels=['L(x)','L\'(x)'],loc='best')
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39