LeetCode刷题之HOT100之数组中的第K个最大元素

2024 6/29 今天天气很好啊，想爬山，奈何下午还有最后的一个汇报。做个题先

1、题目描述

2、算法分析

看到这个题我想到的就是:

  public int findKthLargest(int[] nums, int k) {
        Arrays.sort(nums);
        return nums[nums.length - k ];
    }
1
2
3
4

哈哈，我提交上去击败了67.49%，想点正规的算法。
这个是在考察排序的，下图为八大排序复杂度情况。

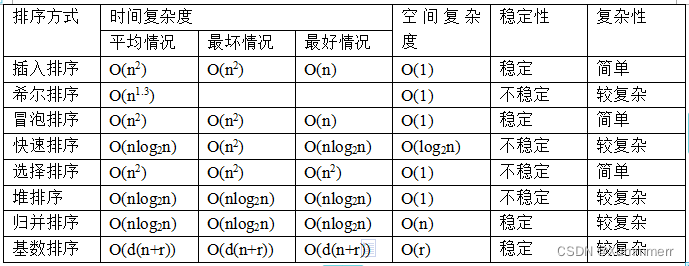
为了将复杂度控制在O(n)层级。what should i do？那就是在快排的基础上稍作改进：
这里是快排：

3、代码

public int quickSort(int[] nums, int left, int rigth, int k){
        if(left == rigth){
            return nums[k];
        }
        int base = nums[left];
        while(left < rigth){
             while(left < rigth && nums[rigth] > base){
                rigth--;
            }
            while(left < rigth && nums[left] < base){
                left++;
            }
            if(left < rigth){
                int temp = nums[left];
                nums[left] = nums[rigth];
                nums[rigth] = temp;
            }
        }
        if(k <= rigth){
            return quickSort(nums, left, rigth, k);
        }else{
            return quickSort(nums, left + 1, rigth, k);
        }
    }
    public int findKthLargest(int[] nums, int k) {
        int n = nums.length;
        return quickSort(nums, 0, n - 1, k);
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

测试时间超出限制，所以需要改进一下：

public int quickSort(int[] nums, int left, int rigth, int k){
        // 当左边界等于右边界时，说明搜索区间只有一个元素，直接返回该元素
        if(left == rigth){
            return nums[k];
        }
        // 选择基准值（这里我们简单选择左边界的元素作为基准）
        int base = nums[left], i = left - 1, j = rigth + 1;
       while (i < j) {
            // 使用do-while循环进行快速选择的分区过程  
            // 将小于基准的元素放到左边，大于基准的元素放到右边
            // 从左向右扫描，找到第一个大于或等于基准的元素  
            do i++; while (nums[i] < base);
            // 从右向左扫描，找到第一个小于或等于基准的元素 
            do j--; while (nums[j] > base);
            // 如果i和j还未相遇，则交换它们
            if (i < j){
                int tmp = nums[i];
                nums[i] = nums[j];
                nums[j] = tmp;
            }
        }
        // j 现在指向小于基准值的最后一个元素的右边一个位置  
        // 如果 k 的值小于或等于这个位置（即 k 指向的元素在基准值的左边或与其相等），  
        // 则第k大的元素在左半部分，递归搜索左半部分 
        if (k <= j) return quickSort(nums, left, j, k);
        // 否则，第k大的元素在右半部分，递归搜索右半部分  
        // 注意：k的值不需要改变，因为我们是基于当前搜索范围的索引来搜索的
        else return quickSort(nums, j + 1, rigth, k);
    }
    public int findKthLargest(int[] nums, int k) {
        int n = nums.length;
        return quickSort(nums, 0, n - 1, n - k );
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

官方的题解真的规范性太差了，anyway，就到这儿吧

4、复杂度分析

• 时间复杂度：O(n)。
• 空间复杂度：O(logn)，递归使用栈空间的空间代价的期望为 O(logn)。