【论文阅读——联邦学习场景下基于参与方贡献的激励机制】_联邦学习 激励

1. 联邦学习场景下基于参与方贡献的激励机制

本文提出了一种基于公平性的联邦学习激励机制(FedFAIM)。
该机制满足两种公平性：

• 聚合公平性
  • 根据数据质量确定聚合权重。
  • 聚合公平性通过检测本地梯度质量并根据数据质量进行聚合来实现。
• 奖励公平性
  • 为每个参与者分配一个定制化的模型，模型性能与贡献正相关。
  • 奖励公平性通过基于Shapley值的贡献评估以及基于声誉和梯度分布的奖励分配方法实现。

2.该工作面临的三个挑战

• 参与方的本地模型质量可能不稳定，本地模型可能质量较低，这将会对最终聚合的全局模型产生负面影响。
  • 此外，一些参与方可能会有“搭便车”行为，他们在不做任何本地训练的情况下通过上传随机生成的梯度而从全局模型中获益。
  • 此外，可能存在恶意参与方进行投毒攻击，以影响全局模型的参数，导致现有的联邦学习失效。
  • 因此，过滤掉低质量的本地模型至关重要。
• 为了确定每个训练轮次的奖励分配，必须实时评估参与方的贡献。然而，现有贡献评估方法通常基于Shapley值，其指数级的计算开销难以满足实时性。
• 通过给参与方分配与其贡献相匹配的模型来实现ＦＬ的合作公平性与金钱激励有着本质区别。
  • 关键挑战在于同时考虑参与方贡献以及每轮本地梯度和全局梯度的分布为每个参与方分配定制化模型。
  • 这种分配不仅应该准确反映参与方的贡献，而且还应在模型性能和公平性之间实现良好的权衡。

3. 提出FedFAIM

• FedFAIM采用一种新颖的梯度聚合方法。该方法首先使用边际损失进行质量检测以过滤掉低质量的本地梯度，然后通过考虑模型更新的质量确定聚合权重，从而聚合本地梯度。
• FedFAIM引入了基于Shapley值的贡献度量，将本地梯度与全局梯度之间的相似性作为效用函数。通过评估参与方每轮的贡献，计算参与方下一轮分配的模型。该方法的计算复杂度是线性的。
• FedFAIM的奖励分配机制首先基于参与方本地模型质量和贡献计算参与方声誉，来确定分配给每个参与方梯度的数量。然后，它通过考虑本地梯度和全局梯度的分布，从全局梯度中选择相应数量的梯度，构建要分配给每个参与方的模型。该工作进一步证明了FedFAIM奖励分配机制具有理论保证。

3.1 问题描述

该工作考虑横向联邦学习(Horizontal Federated Learning,HFL)情境，该FL系统由两个主要参与方组成：参与方（数据持有者）和FL服务器。该工作将N个参与方的集合表示为 W = { 1 , 2 , . . . , N } W=\{1,2,...,N\} W={1,2,...,N}，并将属于参与方i的私有数据集表示为$D_i$。在FL系统中，模型通过多次迭代来训练。在每轮t中，工作通过为每个参与者分配不同的聚合梯度来代替向传统FL系统中直接从服务器下载全局模型的操作。

每个参与方i根据其本地训练数据优化分配的模型，并将本地梯度$u_i^{(t)}$发送到FL服务器，在收集到所有本地更新 { u i ( t ) } i = 1 N \{u^{(t)}_i\}^N_{i=1} {ui(t)​}i=1N​,服务器将它们聚合成全局梯度$u_G^{(t)}$。然后，评估每个参与方的贡献，并基于奖励机制为每个参与方i分配定制的聚合梯度$u_{\ast i}^{(t)}$。

该训练过程重复进行，直到模型收敛。这种更新后的ＦＬ训练过程使得参与方依据其贡献度不同而获取不同的模型。

3.2 设计概览

该工作提出的FedFAIM实现在FL服务器上，对参与方公开可见，因此该设计可以很容易地被应用于现有的FL系统。FedFAIM增强的HFL系统包括三个主要模块：梯度聚合(GA)、贡献评估(CA)和奖励分配(RA)。
GA包括两个子模块：质量检测和聚合权重计算。
RA中也有两个子模块，即声誉计算和奖励计算。

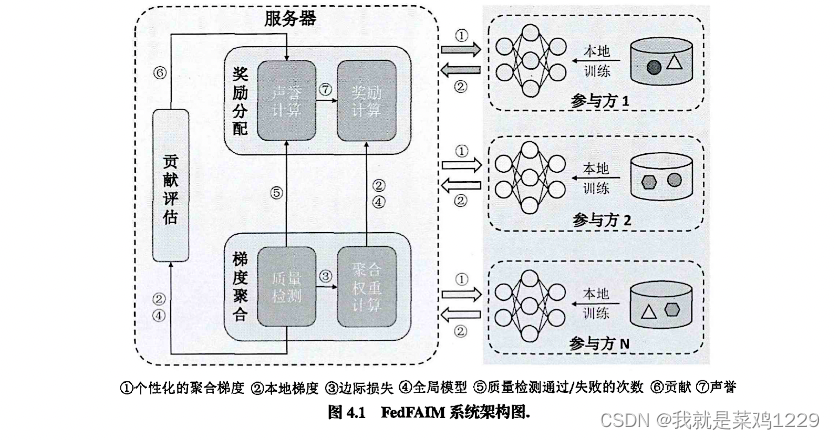
工作流程如下：

• 步骤（1）：在第t轮，参与方i从FL服务器接收到FedFAIM的RA模块分配给其的定制的梯度聚合，随后更新本地模型。
• 步骤（2）：每个参与方i使用本地训练数据$D_i$更新本地梯度$u_i^{(t)}$,并将其上传到服务器。
• 步骤（3）：服务器接收到所有参与方发送的梯度后，质量检测子模块为每个参与者i计算边际损失${\delta }_i^{(t)}$,只有当${\delta }_i^{(t)}$不小于阈值$\delta$时才接受本地梯度$u_i^{(t)}$
• 步骤（4）：服务器将已通过质量检测的所有参与方的边际损失发送到聚合权重计算子模块，并还将这些参与方的质量检测通过/失败的次数发送到声誉计算的子模块。
• 步骤（5）：在接收到边际损失信息后，聚合权重计算子模块根据参与方的边际损失将所选参与方的本地梯度聚合成全局梯度$u_G^{(t)}$。然后，将所有本地梯度和$u_G^{(t)}$发送到CA模块和奖励计算子模块。
• 步骤（6）：在介绍到本地梯度和聚合全局梯度后，CA使用本地梯度$u_i^{(t)}$到聚合全局梯度$u_G^{(t)}$的映射距离作为Shapley值计算中的估值函数，评估每个参与方i的每轮贡献$c_i^{(t)}$。然后，将所有$i$的$c_i^{(t)}$发送到声誉计算子模块。
• 步骤（7）：在接收到质量检测结果和所有参与方的贡献后，声誉计算子模块计算声誉值并将其发送到奖励计算子模块。奖励计算子模块确定每个参与方i的分配梯度数量$nu{m}_i^{(t)}$，并基于$u_i^{(t)}$和全局梯度向量$u_G^{(t)}$的分布从$u_G^{(t)}$中选择$nu{m}_i^{(t)}$个梯度，从而形成分配的聚合梯度$u_{\ast i}^{(t)}$。最后，将$u_{\ast i}^{(t)}$发送给i以进行下一轮训练。

3.3 模型聚合

3.3.1 质量检测

筛选掉低质量模型直观的方法是判断本地模型的损失是否超过给定的损失阈值。然而，随着本地模型在更多的训练迭代中性能的提高，这个阈值需要不断减小，因此难以确定。为解决这个问题，该工作采用了边际损失度量。

在第t轮，该工作使用${\mathcal{M}}_G^{(t)}$表示通过聚合所有参与方的本地模型获得的全局模型，$M_{-i}^{(t)}$表示通过聚合除i之外所有参与方的本地模型获得的全局模型。由于该工作此时不知道他们本地模型质量，因此这里的聚合权重是$\frac{1}{N}$，聚合公式如下:
M G ( t ) = M G ( t ) + 1 N ∑ j u j ( t ) , M − i ( t ) = M G ( t ) + 1 N − 1 ∑ j ∈ W − { i } u j ( t ) , \mathcal{M}^{(t)}_G=\mathcal{M}^{(t)}_G+\frac{1}{N}\sum_ju^{(t)}_j, \newline \mathcal{M}^{(t)}_{-i}=\mathcal{M}^{(t)}_G+\frac{1}{N-1}\sum_{j\in W-\{i\}}u^{(t)}_j, MG(t)​=MG(t)​+N1​j∑​uj(t)​,M−i(t)​=MG(t)​+N−11​j∈W−{i}∑​uj(t)​,

边际损失loss

设$l^{(t)}$和$l_{-i}^{(t)}$分别表示${\mathcal{M}}_G^{(t)}$和${\mathcal{M}}_{-i}^{(t)}$在验证集的损失。参与方i的边际损失定义为：
$${\delta }_i^{(t)}=l_{-i}^{(t)}-l^{(t)}$$
当较高质量的本地模型被聚合时，全局模型的损失将降低。该工作使用$\delta$表示质量阈值，并在${\delta }_i^{(t)}\ge \delta$时接受参与方i的本地模型（代表该模型对于全局模型的贡献比较大）。当阈值$\delta$变化时，该工作在聚合模型上评估测试准确度。最后，该工作使用$Q^{(t)}$记录在第t轮中通过质量检测的参与方集合。另外，该工作使用$n_i^{pass}$和$n_i^{fail}$分别表示参与方i通过和为通过质量检测的次数。

3.3.2 梯度聚合

在每一轮t中，通过质量检测的本地梯度被用于获得更新的全局梯度。这方面广泛采用的方法是FedAvg，聚合步骤如下：
$$u_G^{(t)}=\sum _i\frac{|D_i|u_i^{(t)}}{{\sum }_i|D_i|}$$
$|D_i|$指的是参与方i用于训练本地模型的数据量。

然而，FedAvg在以下情况下可能不起作用：（１）某个参与方有大量但质量较低的数据。根据FedAvg，因为其数据量大而可以获得相对较大的权重，这对于一个数据质量好但数据量较少的参与方来说是不公平的。（２）存在一些恶意参与方。恶意参与方可以伪造数据量大小。根据FedAvg，这些参与方可能直接影响模型聚合中的权重。

为了克服FedAvg的缺点，FedFAIM考虑了数据质量来聚合本地模型更新。该工作使用$m_i^{(t)}$来表示第t轮中参与方i的数据质量，$m_i^{(t)}$根据其边际损失计算出来的。直观上，边际损失较大的本地梯度应该获得较高的权重。因此，在每轮t中，该工作使用带有控制参数$\gamma$的指数函数来确定每个参与方$i$的数据质量，公式4.4如下:
$$m_i^{(t)}=\frac{exp(\gamma {\delta }_i^{(t)})}{{\sum }_{i}exp(\gamma {\delta }_i^{(t)})}$$
为了实现聚合公平性，FedFAIM通过考虑每个参与方i的本地数据质量来确定第t轮中参与方i的聚合权重${\alpha }_i^{(t)}$，公式4.5具体如下：
$${\alpha }_i^{(t)}=\frac{m_i^{(t)}}{{\sum }_i{m}_i^{(t)}}$$
最后，FedFAIM在第t轮中按如下方式将选定的本地梯度聚合到全局模型中，公式4.6如下：
$$u_G^{(t)}=\sum _i{\alpha }_i^{(t)}{u}_i^{(t)}$$

3.3.3 贡献评估

由于FedFAIM通过质量检测筛选掉潜在的低质量梯度，所有被选中的本地梯度都被认为是有价值的。对应所有选中本地梯度的聚合梯度$u_N$期望具有最高的价值。因此，可以利用本地梯度和$u_N$之间的余弦相似度来近似它们的估值函数，公式4.8如下：
$$V(i)=||u_i^{(t)}||cos(u_i^{(t)},u_G^{(t)})$$
然后，按如下方式计算边际估值函数：

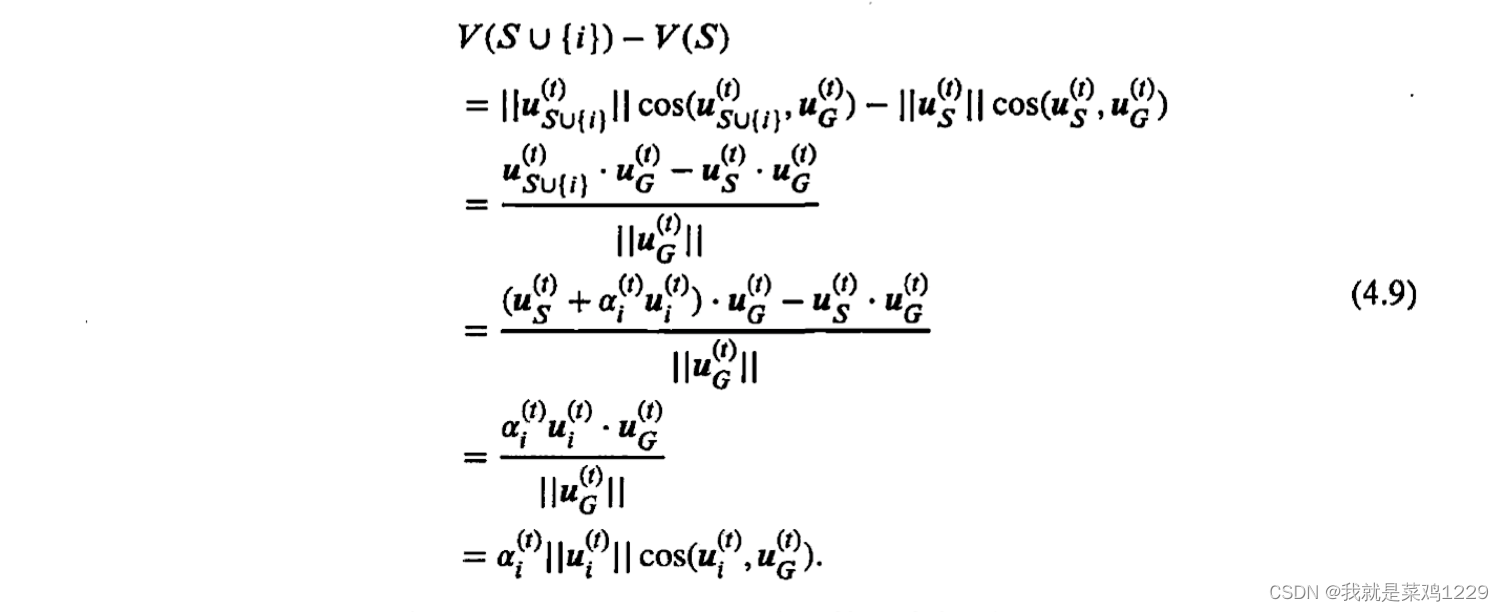
根据公式(4.9)中，可以得出$V(S\cup i)-V(s)$不会随着集合S的内容而改变。因此，不需要遍历S的所有可能子集。结合公式(4.7)和公式(4.9)，可以通过如下方式来计算参与方i在第t轮的贡献值${\varphi }_i^{(t)}$

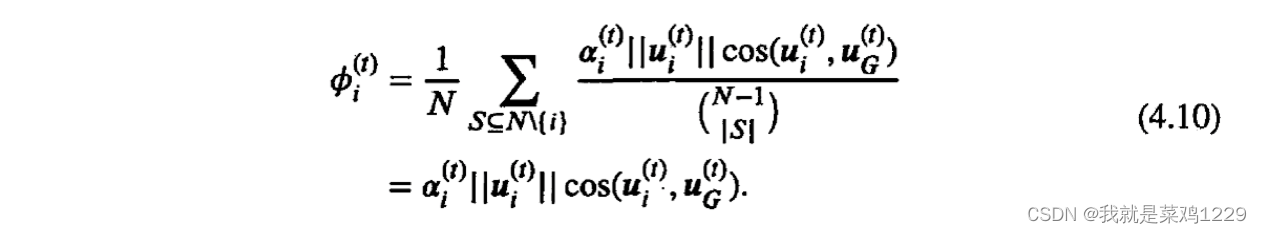
3.4 奖励分配

3.4.1 声誉计算

声誉是一种基于过去的行为来衡量参与方在当前活动中的可靠性或信誉度的常用指标。该指标可以平滑参与方行为中的波动，以建立更客观的行为模式。

该工作根据参与方在从第１轮到第ｔ轮中的贡献和通过质量检测的次数来计算每个参与者$i$的声誉。设$c_i^{(t)}$表示参与方i从第1轮到第t轮的累积贡献，公式如4.11所示：
$$c_i^{(t)}=max(0,\sum _{i=1}^t{\varphi }_i^{(t)})$$
基于当前轮$t$中观察到的最大贡献来定义$i$的相对贡献$z_i^{(t)}$
$$c_i^{(t)}=\frac{c_i^{(t)}}{ma{x}_i(c_i^{(t)})}$$
然后，考虑如何反映质量检测对声誉的影响。该工作使用Gompertz函数来反映质量检测对声誉的影响，因为该函数更适当地模拟了个体之间的信任,定义如下：

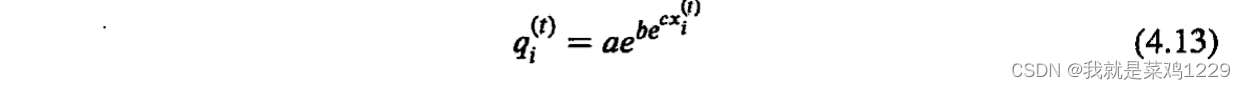
其中$a$指定了上限渐近线，$b$控制ｘ轴上的位移，$c$调整函数的增长率。函数的输出，记为$q_i^{(t)}$，是０和１之间的数字，表示质量检测的影响。
Gompertz函数的输入，记为$x_i^{(t)}$，考虑了每个参与方i的历史质量检测结果。为了确保声誉$q_i$的范围为[0,1]，设置a=1，b= -1，c= -5.5。函数的图像如图4.2所示：

$x_i$应考虑通过/未通过质量检测的次数，按如下公式计算$x_i^{(t)}$:


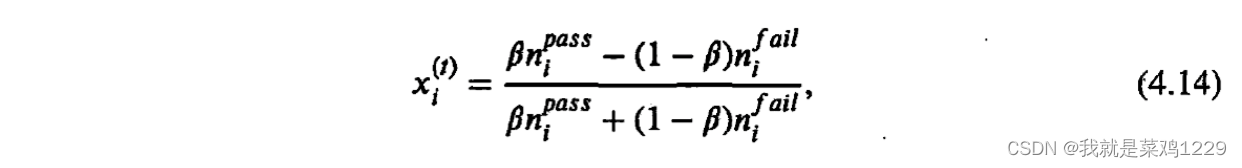
结合公式4.12和公式4.13，可以得到参与方i在t轮中声誉$r_i^{(t)}\in (0,1]$，如公式4.15所示
$$r_i^{(t)}=q_i^{(t)}{z}_i^{(t)}$$

3.4.2 奖励计算

为了设计一个公平的奖励分配方案，参与方应该得到一个反映其声誉的模型版本作为奖励。该工作的想法是通过将聚合模型中的重要梯度数量分配给参与方来控制模型的性能。因此，ＦｅｄＦＡＩＭ奖励分配模块包括两个步骤：１）基于参与者的声誉确定分配给每个参与者的梯度数量$nu{m}_i^{(t)}$ 2）从全局梯度向量$u_G^{(t)}$中选择$nu{m}_i^{(t)}$个重要梯度。

• 步骤(1)：计算分配梯度的数量：基于奖励公平性(定义4.2),可以计算分配梯度的数量如公式4.16所示：
  $$nu{m}_i^{(t)}=\frac{r_i^{(t)}}{ma{x}_i{r}_i^{(t)}}|u_G^{(t)}|$$
  其中，$r_i^{(t)}\in (0,1]$。声誉最高的参与者将获得整个全局模型。
• 步骤(2)：选择相应数量的梯度：对于每个i，FedFAIM从全局梯度向量$u_G^{(t)}$中选择$nu{m}_i^{(t)}$个重要的梯度。
  • 为了衡量全局梯度向量$u_G^{(t)}$中每个梯度项$u_{G,j}^{(t)}$的重要性，定义了两个得分$s_{i,j}^{(t)}$和$u_{G,j}^{(t)}$。
  • $u_{G,j}^{(t)}$代表梯度更新对于全局模型性能的影响
  • $s_{i,j}^{(t)}$由本地梯度$u_i^{(t)}$的分布决定。$u_{i,j}^{(t)}$的绝对值越大，参与者i从全局梯度$u_{G,j}^{(t)}$中获取的分数就越高。因此，$s_{i,j}^{(t)}$如下面的公式4.17所示：
    $$s_{i,j}^{(t)}=\frac{|u_{i,j}^{(t)}|}{{\sum }_j|u_{i,j}^{(t)}|}$$
  • $s_{G,j}^{(t)}$由全局梯度$u_G^{(t)}$的分布决定。$u_{G,j}^{(t)}$的绝对值越大，它对全局模型性能的影响就越大。基于这个直觉，$u_{G,j}^{(t)}$如下面的公式4.18所示：
    $$u_{G,j}^{(t)}=\frac{|u_{G,j}^{(t)}|}{{\sum }_j|u_{G,j}^{(t)}|}$$
  • 令$s_j^{(t)}$为全局梯度向量$u_G^{(t)}$中每个梯度项$u_{G,j}^{(t)}$的总体得分，可以计算为：
    $$s_j^{(t)}=s_{i,j}^{(t)}\times s_{G,j}^{(t)}$$
    最后，对于每个参与者i，FedFAIM按照其$s_j^{(t)}$得分的降序对全局梯度向量$u_G^{(t)}$中的梯度项$s_{G,j}^{(t)}$进行排名，并选择排名前$nu{m}_i^{(t)}$个梯度，形成i在第t轮的分配梯度向量$u_{\ast i}^{(t)}$。
    

4.实验评估

数据集：

• 图像分类数据集
  • MNIST
  • CIFAR10
• 文本分类数据集
  • Stanford情感库(SST)

4.1 数据集拆分

• 均匀分布
  • 数量相等/同分布数据
• 不平衡的数据集大小
  • 数量不等/同分布
• 不平衡的类别数
  • 数量相同/不同分布(有的数据集中只有几类)
• 嘈杂标签
  • 拥有不同百分比的错误标签

4.2 对比的方法

• 梯度聚合效果
  • FedFAIM
    • 考虑了数据质量来聚合本地模型更新
  • FedAvg
    • 基于本地数据集的大小确定聚合权重
  • FairAvg
    • 为所有参与方分配相等的权重
  • FedQD
    • 基于本地模型的损失确定聚合权重
• 贡献评估
  • CI
    • 提出了一个贡献指数来评估每个参与方的贡献，通过使用中间的ＦＬ模型更新重构模型。
  • TMC-Shapley
    • 采用样本方法，并专注于提高计算效率
  • GTB
    • 提出了一系列有效的算法来近似Shapley值
  • COS-SIM
    • 引入了一个附加误差来近似Shapley值
• 奖励分配
  • Standalone
    • 参与方仅使用其各自的本地数据集训练其模型。
  • FedAvg
    • 分配相同的模型给所有参与方，不考虑他们的贡献。
  • CFFL
    • 使用模型准确性作为贡献指数
    • 获得一个反映其贡献的最终模型
  • RFFL
    • 基于声誉的方法来评估贡献
    • 获得一个反映其贡献的最终模型
• 评估指标
  • 测试准确率
    • 使用测试准确率作为梯度聚合和奖励分配的性能指标
  • 运行时间
    • 使用运行时间来比较贡献评估方法的效率
  • 皮尔森相关系数PCC
  • Jain’s Fairness Index
    • 该工作使用JFI来衡量奖励分配方法的公平性

5. 小结

该工作提出了第一个满足聚合公平性和奖励公平性的联邦学习非金钱激励机制一FedFAIM，以激励存在竞争关系的参与方参加联邦学习训练。首先，FedFAIM采用梯度边际损失来检测各个参与方本地的数据质量，并基于质量进行模型聚合以实现聚合公平性。而后，FedFAIM采用Shapley值的近似算法评估各个参与方的贡献，并基于贡献以及参与方的本地数据质量计算参与方的声誉。最后，FedFAIM基于参与方的声誉以及梯度分布给每个参与方分配一个定制化的模型，以实现奖励公平性。此外，该工作证明了奖励公平性可以在理论上得到保证。大量的实验表明，与类似的联邦学习非金钱激励机制相比，FedFAIM在保证公平性的同时，进一步提高了参与方获得的模型精度。

搬运论文出处：面向数据交易供给侧的激励机制研究。