【插入类排序】直接插入排序、希尔排序、性能测试_设计直接插入排序的算法,输出每一趟排序结果。并用相关数据进行测试。

1. 直接插入排序

直接插入排序是一种比较简单的插入排序方法，其基本思想是：把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中，直到所有的记录插入完为止，得到一个新的有序序列

我们玩扑克牌时，就用到了直接插入排序

动态演示插入排序

代码实现

void InsertSort(int* arr, int sz)
{
	//一共sz-1躺
	for (int i = 0; i < sz - 1; i++)
	{
		//一趟排序
		int end = i;
		int x = arr[end + 1];
		while (end >= 0)
		{
			//有序数组最后一个元素大于待插入元素
			if (x < arr[end])
			{
				//大于x的元素向后挪动
				arr[end + 1] = arr[end];
				end--;
			}
			else break;
		}
		//插入x
		arr[end + 1] = x;
	}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

由于第一个数据本身是有序的，所以有2个数据时需要1趟排序，sz个数据需要$sz-1$趟排序

直接插入排序的特性

1. 元素越接近有序，直接插入排序算法的时间效率越高，最好情况下执行循环$sz-1$次
2. 时间复杂度$O(n^2)$
3. 空间复杂度$O(1$)
4. 稳定性：稳定

大部分情况下数组是无序的因此直接插的时间复杂度往往达到$O(n^2)$,这样的效率不高，所以我们有另外一种排序希尔排序可以达到减少排序时间的效果

2. 希尔排序(缩小增量排序)

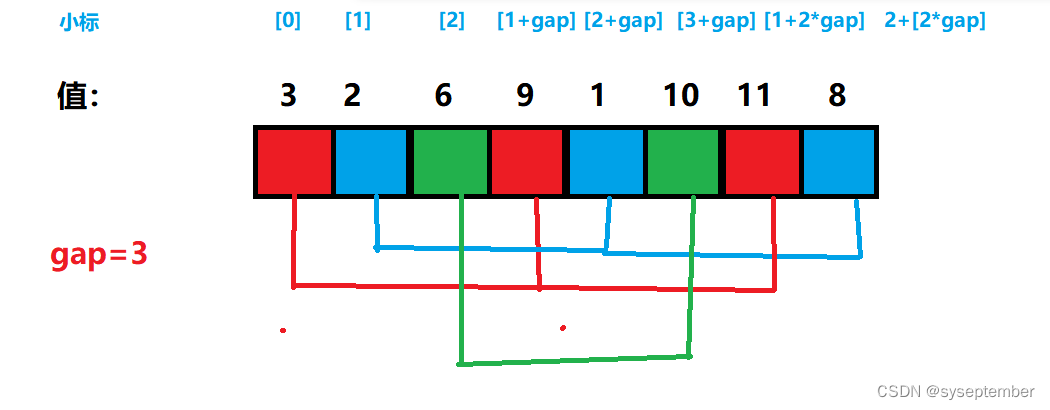
希尔排序法又称缩小增量法。希尔排序法的基本思想是：先选定一个整数gap，把待排序数据中所有数据分成gap组，所有距离为gap的数据分在同一组内，并对每一组内的记录进行排序。然后重复上述分组和排序的工作。当gap为1时，就是直接直接插入排序。

可以看见希尔排序主要分如下几步

1. 将数据分为gap组
2. 对每一组数据进行插入排序
3. 重复1、2保证每次的gap比之前小并且gap最后取得1完成直接插入排序

1. 分组

定义一个gap变量,gap变量表示每组中的元素在待排序数组中相差几个数

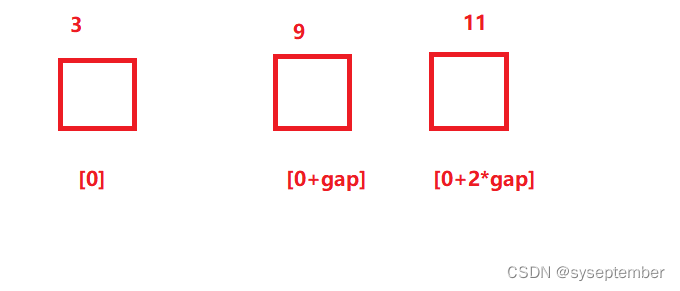
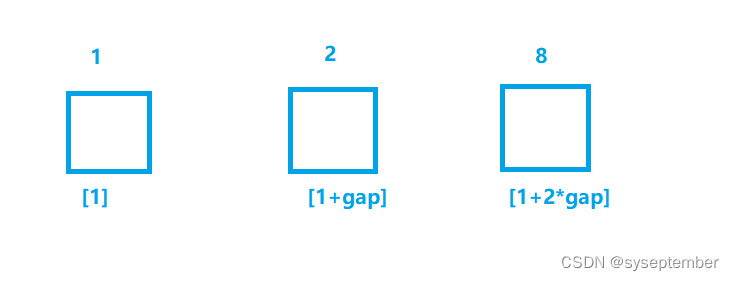
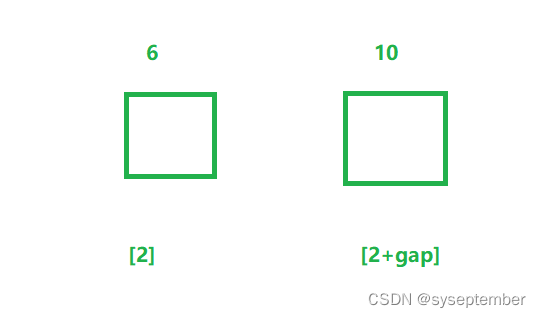
其中颜色相同的为一组，可以发现一共有gap组

2. 对每组执行插入排序

红组执行插入排序后的结果

蓝组执行插入排序后的结果

绿组执行插入排序后的结果

最终对3组分别执行插入排序后的结果

与最开始相比变得更加有序了，因为每组都是有序的

3. 重复

重复1、2，继续将待排序数组以gap进行分组，不过此时待排序数组是以3为分组的有序数组，所以gap不能再取3，gap每次的选择必须比前一次小，这样才能保证数组没经过一次插入更加的靠近有序，最终要使得gap取到1，这样才可以保证最后一次排序之后数组完全有序，因为当gap取得1时就是直接插入排序

既然最后还是需要直接插入排序，为什么说希尔排序的效率高于直接插入呢？

因为希尔排序在gap取到1之前，gap已经取过3,5……，而gap每次减少时都会保证待排序数组更加有序，也就是说，当gap取到1时数组已经非常有序了，只有极个别的元素不在对应的位置，最后需要gap=1来时这些元素排到相应的位置，如果直接插入排序，每次的插入都可能耗费大量的时间

总结原因：

1. 当gap值很大时数据项每一趟排序需要移动的个数很少，但数据项的距离很长。
2. 当gap值减小时每一趟需要移动的数据增多，此时已经接近于它们排序后的最终位置

无论是gap值较小时还是较大时希尔排序总是比直接插入执行的循环次数少，希尔排序的时间复杂度一定小于$O(N^2)$
大量的实验表明，希尔排序的时间复杂度为$O(N^{1.3})$,但是针对于给定的待排序数组，时间复杂度无法算出来是因为gap的值都会影响数据的有序性，这个影响量度随gap变化而变化，因而我们无法衡量

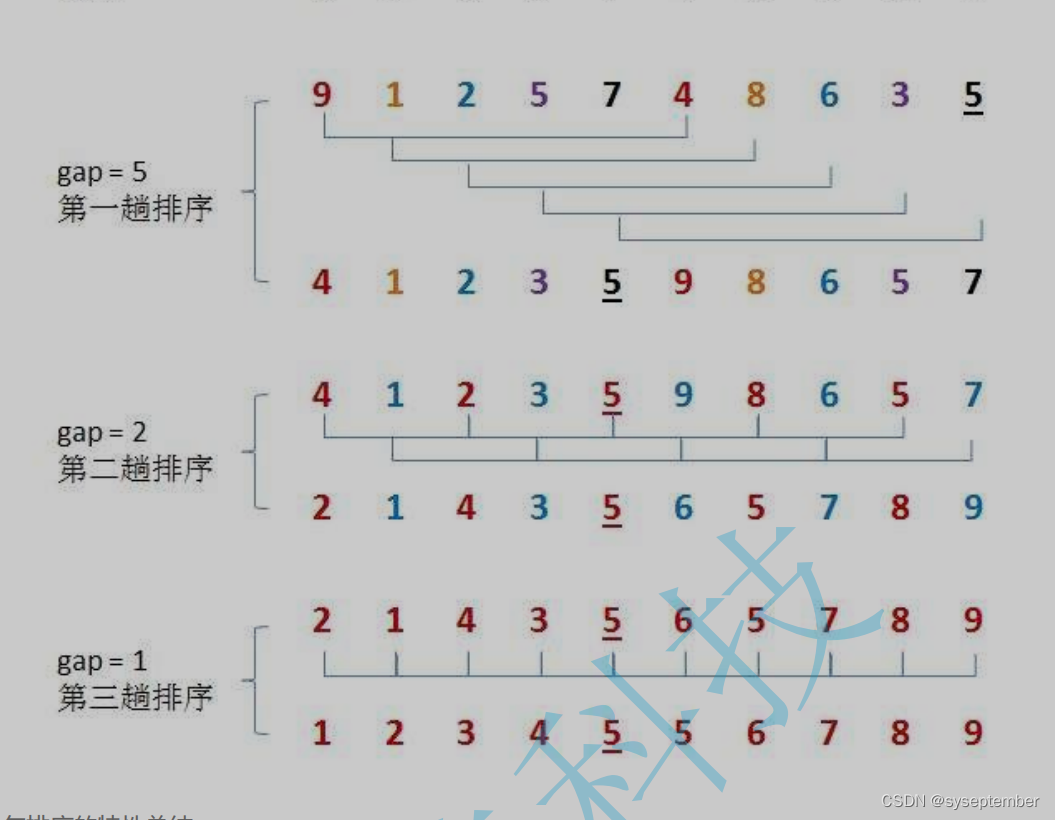
动态演示希尔排序

代码实现

void ShellSort(int* arr, int sz)
{
	//当gap为1时执行的是插入排序，保证数组一定是有序的
	int gap = sz;
	while (gap > 1)
	{
		gap /= 2;
		//gap = gap / 3 + 1;
		//分gap组进行预排序		
		//循环gap次，将每组都进行插入排序
		for (int j = 0; j < gap; j++)
		{
			//一组的插入排序
			for (int i = j; i < sz - gap; i += gap)
			{
				int end = i;
				int x = arr[end + gap];
				//一组的一趟插入排序
				while (end >= 0)
				{
					if (x < arr[end])
					{
						arr[end + gap] = arr[end];
						end -= gap;
					}
					else break;
				}
				arr[end + gap] = x;
			}
		
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

注意理解边界条件，若无法理解则只需要直到将直接插入排序中的end+1,end–里面的1换成gap即可

此代码可以简化成

void ShellSort(int* arr, int sz)
{
	//当gap为1时执行的是插入排序，保证数组一定是有序的
	int gap = sz;
	while (gap > 1)
	{
		gap /= 2;
		//gap = gap / 3 + 1;
		//分gap组进行预排序		
		//循环gap次，将每组都进行插入排序
		for (int i = 0; i < sz - gap; i++)
		{
			int end = i;
			int x = arr[end + gap];
			while (end >= 0)
			{
				if (arr[end] > x)
				{
					arr[end + gap] = arr[end];
					end -= gap;
				}
				else break;
			}
			arr[end + gap] = x;
		}
	}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

希尔排序时间复杂度

1. 希尔排序是对直接插入排序的优化。
2. 当gap > 1时都是预排序，目的是让数组更接近于有序。当gap == 1时，数组已经接近有序的了，这样就
   会很快。这样整体而言，可以达到优化的效果。我们实现后可以进行性能测试的对比。
3. 希尔排序的时间复杂度不好计算，因为gap的取值方法很多，导致很难去计算，因此在好些树中给出的
   
   
   我们可以按照希尔排序的时间复杂度为$O(N^{1.25})O(1.6N^{1.25})$来算
4. 稳定性：不稳定

性能测试

我们来写一个函数来评估直接插入排序和希尔排序的时间效率差异

void TextOP()
{
	srand(time(NULL));
	const int N = 100000;
	int* a1 = (int*)malloc(sizeof(int) * N);
	int* a2 = (int*)malloc(sizeof(int) * N);
	int* a3 = (int*)malloc(sizeof(int) * N);
	int* a4 = (int*)malloc(sizeof(int) * N);
	int* a5 = (int*)malloc(sizeof(int) * N);
	int* a6 = (int*)malloc(sizeof(int) * N);
	int* a7 = (int*)malloc(sizeof(int) * N);
	//随机生成100000个数
	for (int i = 0; i < N; i++)
	{
		a1[i] = rand();
		a2[i] = a1[i];
		a3[i] = a1[i];
		a4[i] = a1[i];
		a5[i] = a1[i];
		a6[i] = a1[i];
		a7[i] = a1[i];
	}

	size_t start1 = clock();//获取调用InsertSort前的系统时间
	InsertSort(a1, N);
	size_t end1 = clock();//获取调用InsertSort后的系统时间

	size_t start2 = clock();//获取调用ShellSort前的系统时间
	ShellSort(a2, N);
	size_t end2 = clock();//获取调用ShellSort后的系统时间

	size_t start3 = clock();
	SelectSort(a3, N);
	size_t end3 = clock();


	printf("InsertSort:%u\n", end1 - start1);
	printf("ShellSort:%u\n", end2 - start2);
	printf("SelectSort:%u\n", end3 - start3);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41