c语言 二分查找（迭代与递归）

        二分搜索被定义为一种在排序数组中使用的搜索算法，通过重复将搜索间隔一分为二。二分查找的思想是利用数组已排序的信息，将时间复杂度降低到O(log N)。

 二分查找算法示例

何时在数据结构中应用二分查找的条件：
应用二分查找算法：
        1、数据结构必须是有序的。
        2、访问数据结构的任何元素都需要恒定的时间。
二分查找算法：

 在这个算法中， 通过查找中间索引“mid”将搜索空间分为两半。 

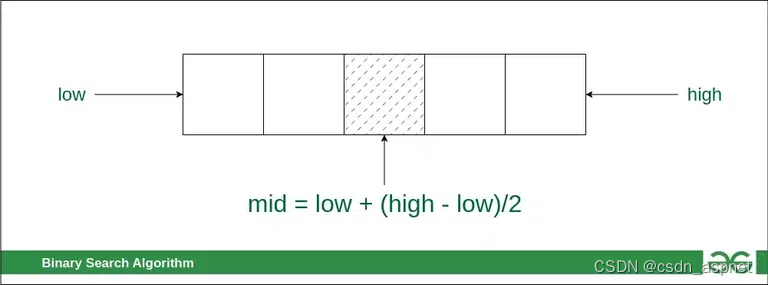
在二分查找算法中查找中间索引“mid” 

1、将搜索空间的中间元素与键进行比较。 
2、如果在中间元素找到密钥，则过程终止。
3、如果在中间元素没有找到键，则选择哪一半将用作下一个搜索空间。
        3.1、如果键小于中间元素，则使用左侧进行下一步搜索。
        3.2、如果键大于中间元素，则使用右侧进行下一步搜索。
4、这个过程一直持续到找到密钥或者总搜索空间耗尽为止。 

二分查找如何工作？
要了解二分搜索的工作原理，请考虑下图：
考虑一个数组arr[] = {2, 5, 8, 12, 16, 23, 38, 56, 72, 91}，目标 = 23。
第一步：计算mid并将mid元素与key进行比较。如果键小于 mid 元素，则向左移动，如果大于 mid 则将搜索空间向右移动。
    键（即 23）大于当前中间元素（即 16）。搜索空间向右移动。

二分查找算法：将键与 16 进行比较

        密钥小于当前的中间 56。搜索空间向左移动。 

 二分查找算法：将键与 56 进行比较

 第二步：如果key与mid元素的值匹配，则找到该元素并停止搜索。

 二分搜索算法：与 mid 的关键匹配

如何实现二分查找？
二分查找算法可以通过以下两种方式实现
        1、迭代二分搜索算法
        2、递归二分查找算法
下面给出了这些方法的伪代码。

1.迭代二分查找算法：
        这里我们使用 while 循环来继续比较键并将搜索空间分成两半的过程。
迭代二分搜索算法的实现： 

// C program to implement iterative Binary Search
#include <stdio.h>
 
// An iterative binary search function.
int binarySearch(int arr[], int l, int r, int x)
{
    while (l <= r) {
        int m = l + (r - l) / 2;
 
        // Check if x is present at mid
        if (arr[m] == x)
            return m;
 
        // If x greater, ignore left half
        if (arr[m] < x)
            l = m + 1;
 
        // If x is smaller, ignore right half
        else
            r = m - 1;
    }
 
    // If we reach here, then element was not present
    return -1;
}
 
// Driver code
int main(void)
{
    int arr[] = { 2, 3, 4, 10, 40 };
    int n = sizeof(arr) / sizeof(arr[0]);
    int x = 10;
    int result = binarySearch(arr, 0, n - 1, x);
    (result == -1) ? printf("Element is not present"
                            " in array")
                   : printf("Element is present at "
                            "index %d",
                            result);
    return 0;
}

输出
元素出现在索引 3 处

时间复杂度： O(log N)
辅助空间： O(1)

2.递归二分查找算法：
创建一个递归函数并将搜索空间的中间部分与键进行比较。并根据结果返回找到键的索引或调用下一个搜索空间的递归函数。
递归二分查找算法的实现：

// C program to implement recursive Binary Search
#include <stdio.h>
 
// A recursive binary search function. It returns
// location of x in given array arr[l..r] is present,
// otherwise -1
int binarySearch(int arr[], int l, int r, int x)
{
    if (r >= l) {
        int mid = l + (r - l) / 2;
 
        // If the element is present at the middle
        // itself
        if (arr[mid] == x)
            return mid;
 
        // If element is smaller than mid, then
        // it can only be present in left subarray
        if (arr[mid] > x)
            return binarySearch(arr, l, mid - 1, x);
 
        // Else the element can only be present
        // in right subarray
        return binarySearch(arr, mid + 1, r, x);
    }
 
    // We reach here when element is not
    // present in array
    return -1;
}
 
// Driver code
int main()
{
    int arr[] = { 2, 3, 4, 10, 40 };
    int n = sizeof(arr) / sizeof(arr[0]);
    int x = 10;
    int result = binarySearch(arr, 0, n - 1, x);
    (result == -1)
        ? printf("Element is not present in array")
        : printf("Element is present at index %d", result);
    return 0;
}

输出
元素出现在索引 3 处

二分查找的复杂度分析：
时间复杂度： 
        最佳情况：O(1)
        平均情况：O(log N)
        最坏情况：O(log N)
辅助空间：

O(1)，如果考虑递归调用栈则辅助空间为O(logN)。
二分查找的优点：
        二分查找比线性查找更快，特别是对于大型数组。
        比具有类似时间复杂度的其他搜索算法（例如插值搜索或指数搜索）更有效。
        二分搜索非常适合搜索存储在外部存储器（例如硬盘驱动器或云中）中的大型数据集。
二分查找的缺点：
        数组应该是排序的。
        二分查找要求将要查找的数据结构存储在连续的内存位置中。 
        二分查找要求数组的元素是可比较的，这意味着它们必须能够排序。
二分查找的应用：
        二分搜索可以用作机器学习中使用的更复杂算法的构建块，例如训练神经网络或查找模型的最佳超参数的算法。
        它可用于计算机图形学中的搜索，例如光线追踪或纹理映射的算法。
        它可用于搜索数据库。