「算法」前缀和

前缀和主要解决求数组中某段区间元素和的问题，使用前缀和解决问题的步骤如下:

1. 预处理一个前缀和数组
2. 使用这个数组

一维前缀和

现在有一个一维数组nums

• 预处理前缀和数组
  定义一个数组 dp[]，dp[i]表示 nums 中 [0,i-1] 区间的元素和，那我们就有 dp[i] == dp[i-1] + nums[i-1]这个递推关系
  然后就可以来初始化 dp 数组：

for(int i = 1;i <= len;i++) 
	dp[i] = dp[i-1]+nums[i-1];
1
2

这里的 dp 数组我们从下标为1处开始放值，这是因为如果 i 为 0，那 i-1 就非法了，所以我们从1开始，这样就不用单独讨论 i 为 0 的情况（注意 dp 的长度应比 nums 多1，而且循环的范围是[1, len] ）

• 使用前缀和数组
  接下来使用处理好的前缀和数组，用下面的模板题来演示一下：
  区域和检索——数组不可变

前缀和不难，主要是不同数组间下标的映射关系不好理解，比如题中要我们求 nums 的[left,right]的和，nums 的 left 对应到 dp 中的下标是 left + 1，right 对应 right + 1，所以这个区间的和就是dp[right+1]-dp[left]，用文字解释就是 nums 的 0 到 right 的区间和减掉 0 到 left - 1 的 区间和
代码如下：

class NumArray {
    int[] dp;
    public NumArray(int[] nums) {
        int len = nums.length;
        dp = new int[len+1];
        for(int i = 1;i <= len;i++) dp[i] = dp[i-1]+nums[i-1];
    }
    
    public int sumRange(int left, int right) {
        return dp[right+1]-dp[left];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

二维前缀和

以一道模板题展开讲解：
二维区域和检索——矩阵不可变

与处理一维数组一样，在处理二维数组的时候，我们行和列都从下标为1处开始
要算[i,j]处的前缀和，我们通过下图的方式来计算（这里直接贴力扣官方题解的图了，官方的图比较好看，不过官方的题解真的就是一坨…）：

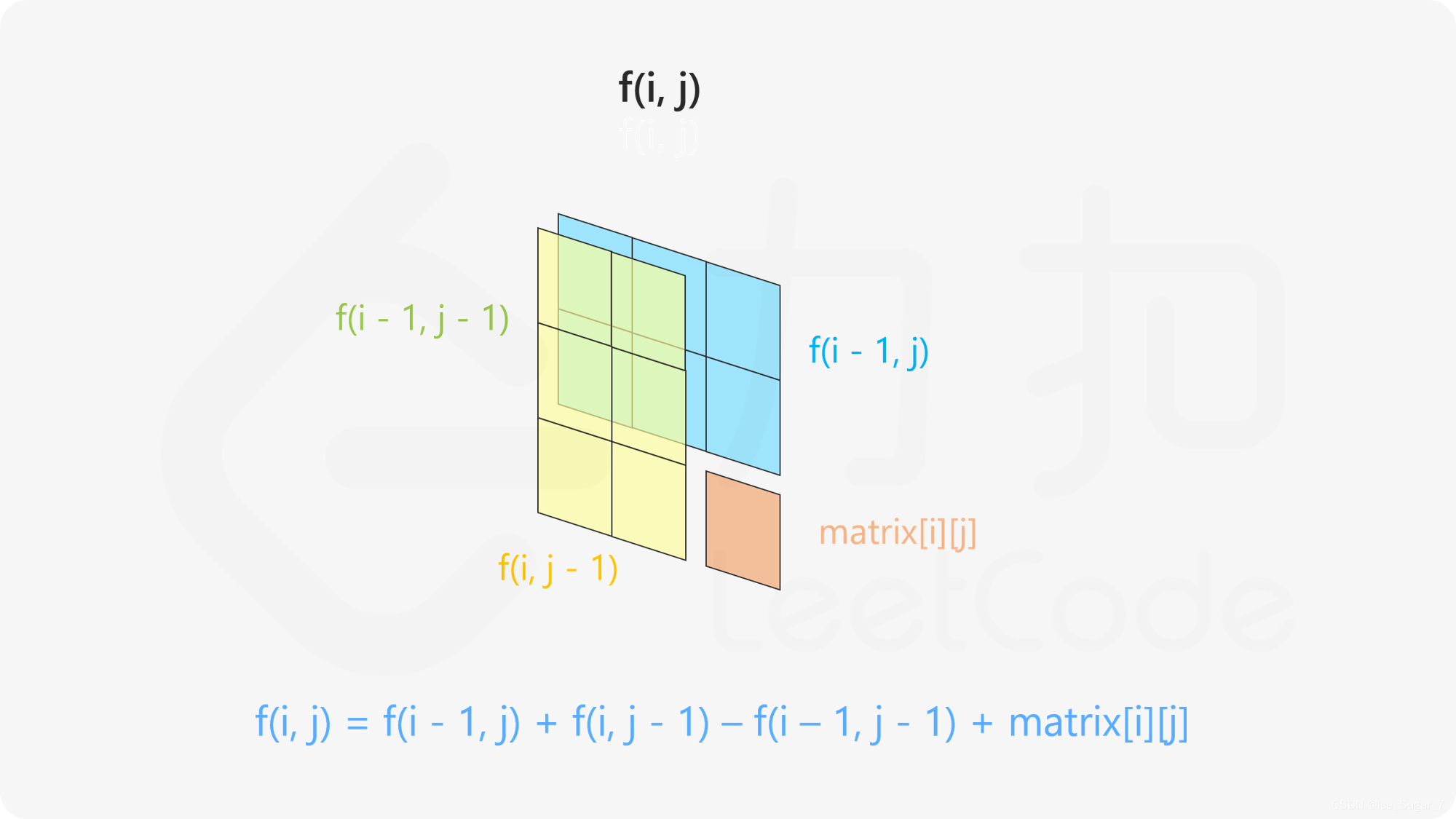
简单来说就是有个地方算重复了，这块地方就是黄色和蓝色重叠的绿色部分：f[i-1][j-1]，需要把它减掉

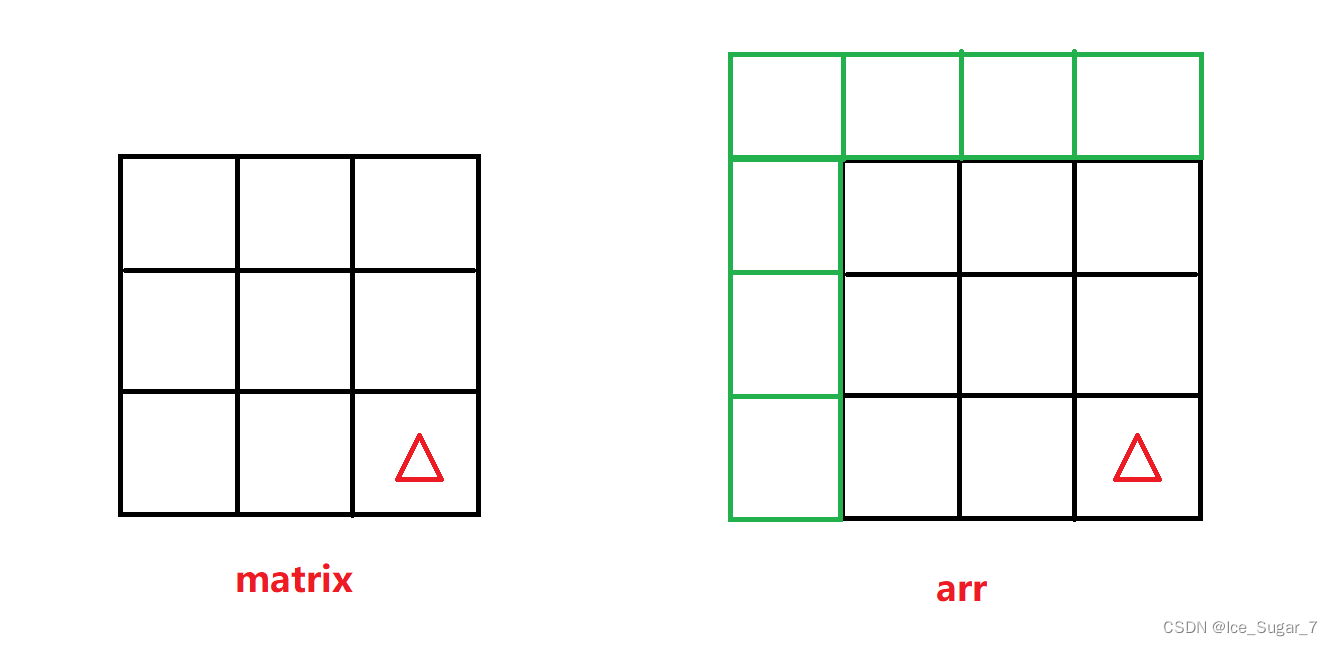
此外还要注意下标的映射关系，因为前缀和数组多定义了一行一列，所以原数组matrix[i][j]的前缀和，应该放到前缀和数组arr[i+1][j+1]处。比如对于arr中（3,3）处的元素，它其实对应的是matrix中的（2,2）
图示如下，其中绿色部分就是为了避免讨论边界情况而多定义的一行和一列，注意辨别两个数组中三角形的下标

构造二维前缀和数组的方法如下：

	public NumMatrix(int[][] matrix) {
        int m = matrix.length;
        int n = matrix[0].length;
        arr = new int[m+1][n+1];
        for(int i = 1;i <= m;i++) {
            for(int j = 1;j <= n;j++) {
                arr[i][j] = arr[i][j-1] + arr[i-1][j] - arr[i-1][j-1] + matrix[i-1][j-1];
            }
        }
	}
1
2
3
4
5
6
7
8
9
10

构造完之后，接下来就要使用它

这道模板题要我们求原数组中（x1，y1）到（x2，y2）之间的区域的元素和，其实也就模仿刚才计算前缀和的方式进行计算：

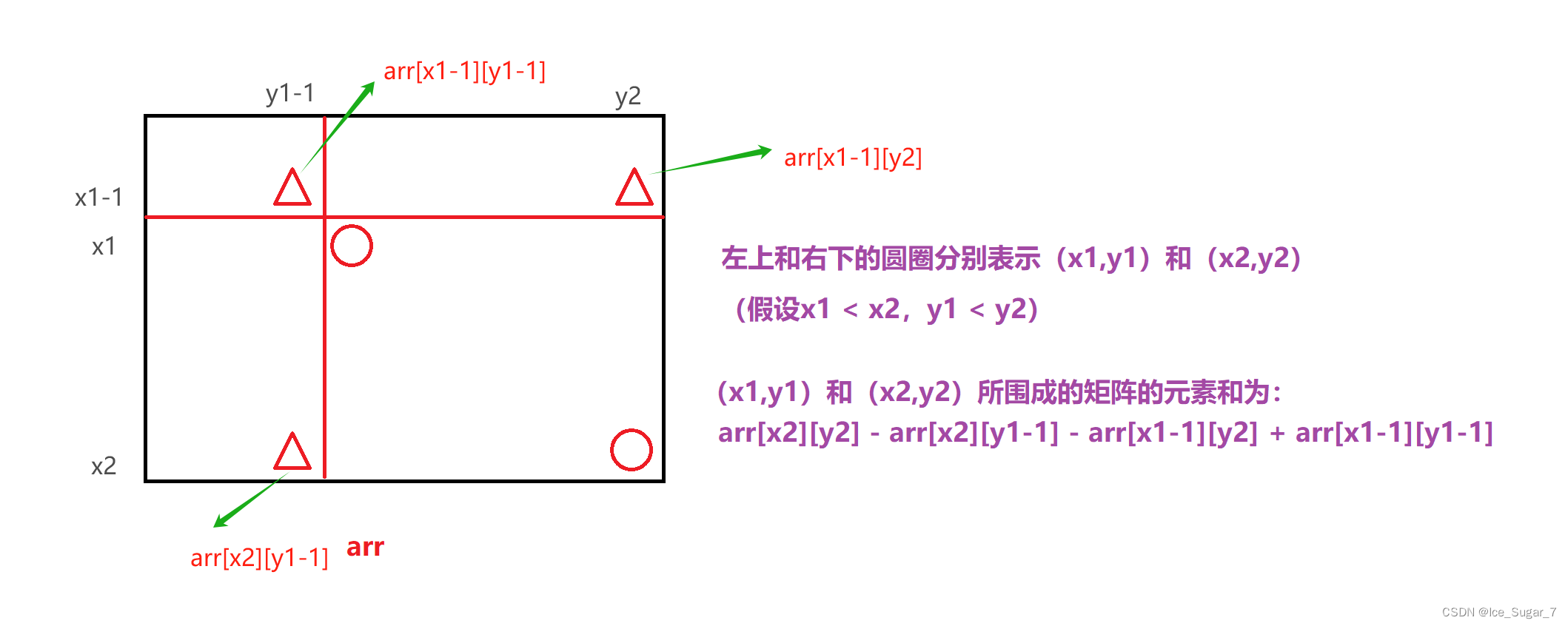
注意 sumRegion 方法的参数，是原数组的下标，我们要根据映射关系转化为前缀和数组的下标，将四个坐标都加1就ok了

代码如下：

    public int sumRegion(int row1, int col1, int row2, int col2) {
        x1++; y1++; x2++; y2++;
        return arr[x2][y2] - arr[x2][y1-1] - arr[x1-1][y2] + arr[x1-1][y1-1];
    }
1
2
3
4

整道题的代码为：

class NumMatrix {
    int[][] arr;

    public NumMatrix(int[][] matrix) {
        int m = matrix.length;
        int n = matrix[0].length;
        arr = new int[m+1][n+1];
        for(int i = 1;i <= m;i++) {
            for(int j = 1;j <= n;j++) {
                arr[i][j] = arr[i][j-1] + arr[i-1][j]+ matrix[i-1][j-1] - arr[i-1][j-1];
            }
        }
    }
    
    public int sumRegion(int x1, int y1, int x2, int y2) {
        x1++; y1++; x2++; y2++;
        return arr[x2][y2] - arr[x2][y1-1] - arr[x1-1][y2] + arr[x1-1][y1-1];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19