2021数学建模国赛B题《对乙醇偶合制备 C4 烯烃的问题研究》省一，第一次参加分享经验_乙醇偶合制备c4烯烃数学建模论文

     

目录

1、摘要

2、问题重述

3、问题分析

4、模型的建立与求解

        数学建模成绩不久前出来了，运气比较好得了省一。参加之前没有任何培训训练，甚至连小组成员长啥样子都不知道，小白第一次参加数学建模分享一下自己的经验。

需要论文或者支撑材料可点下面的链接自行下载：

数学建模对乙醇偶合制备C4烯烃的问题研究-Python文档类资源-CSDN下载

数学建模对乙醇偶合制备C4烯烃的问题研究支撑材料-统计分析文档类资源-CSDN下载

1、摘要

        很重要！摘要放在论文写完最后写。摘要不是提纲，摘要应把论文的主要思想方法、结论和模型的特色讲清楚。让人看到论文的新意。摘要是给读者和评阅专家的第一印象，直接影响到能否获奖的重要因素。建议多看一些历届建模优秀获奖论文，写的时候可以参考着他们的写作思路。

        包括： a. 模型的数学归类（在数学上属于什么类型）；

                    b. 建模的思想（思路）；

                    c. 算法思想（求解思路）；

                    d. 建模特点（模型优点，建模思想或方法，算法特点，结果检验，灵敏度分析，模型      检验…….）；

                    e. 主要结果（数值结果，结论）（回答题目所问的全部“问题”）
  ▲表述：准确、简明、条理清晰、合乎语法、字体工整漂亮；打印最好，但要求符合文章格式。务必认真校对。

    

2、 问题重述

内容要点：

1、问题背景：结合时代、社会、民生等

2、需要解决的问题

 3、问题分析

内容要点：什么问题、需要建立什么样的模型、用什么方法来求解

模型假设略

4、模型的建立与求解

        模型的建立对于每一个模型的建立，需要写出的内容：问题分析→公式推导→基本模型→最终或简化模型。基本模型要有数学公式、方案等。简化模型要明确说明简化思想、依据。

写作要点：

数学建模面临的、要解决的是实际问题，不追求数学上：高（级）、深（刻）、难（度大）。模型要实用，有效，以解决问题有效为原则。

1、能用初等方法解决的、就不用高级方法

2、能用简单方法解决的，就不用复杂方法

3、能用被更多人看懂、理解的方法，就不用只能少数人看懂、理解的方法

4、鼓励创新，但要切实，不要离题搞标新立异

        模型求解每一块内容包括：计算方法设计或选择、算法设计或选择、 算法思想依据、步骤及实现、计算框图、所采用的软件名称

写作要求：

1、需要建立数学命题时：命题叙述要符合数学命题的表述规范，尽可能论证严密

2、需要说明计算方法或算法的原理、思想、依据、步骤。若采用现有软件，说明采用此软件的理由，软件名称

3、计算过程，中间结果可要可不要的，不要列出

4、设法算出合理的数值结果

5、最终数值结果的正确性或合理性是第一位的

6、对数值结果或模拟结果进行必要的检验。结果不正确、不合理、或误差大时，分析原因，  对算法、计算方法、或模型进行修正、改进

7、题目中要求回答的问题，数值结果，结论，须一一列出

8、列数据问题：考虑是否需要列出多组数据，或额外数据对数据进行比较、分析，为各种方案的提出提供依据

9、结果表示：要集中，一目了然，直观，便于比较分析

         ▲数值结果表示：精心设计表格；可能的话，用图形图表形式

         ▲求解方案，用图示更好

10、必要时对问题解答，作定性或规律性的讨论。最后结论要明确

问题一：

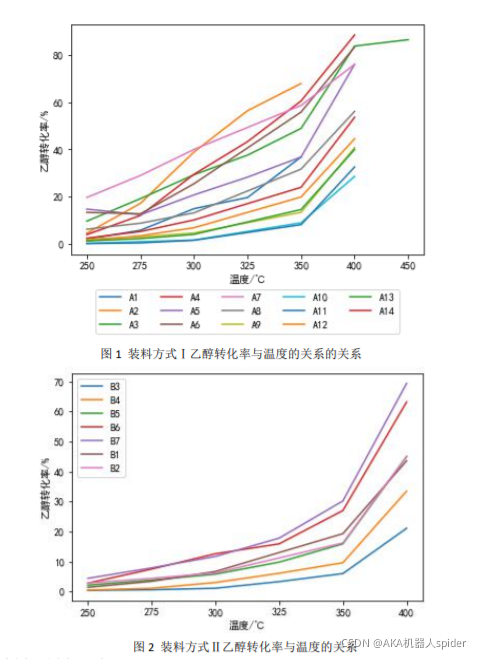
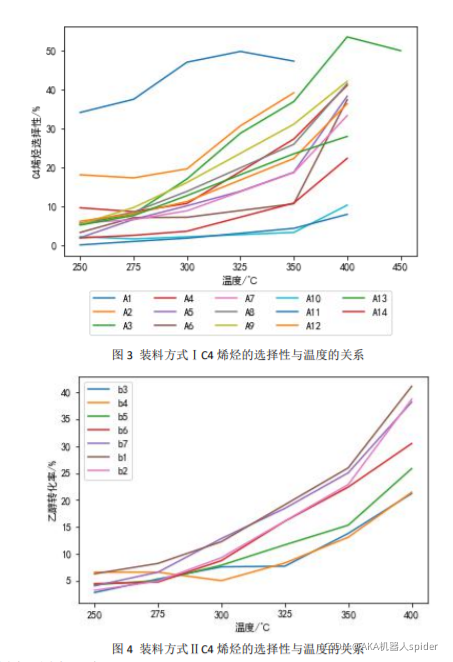
问题二：

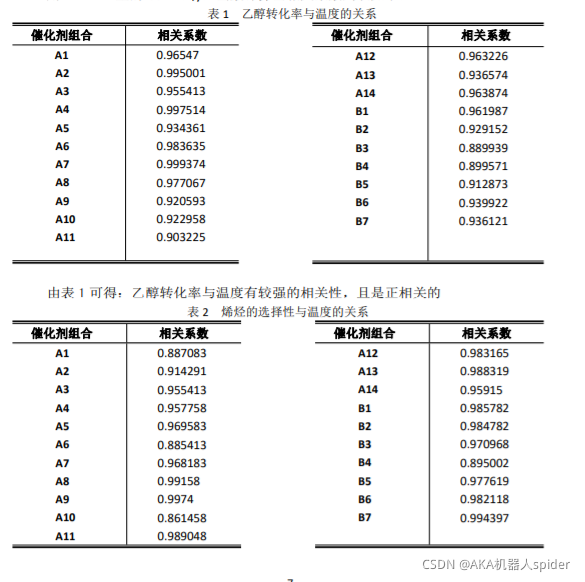
问题三：

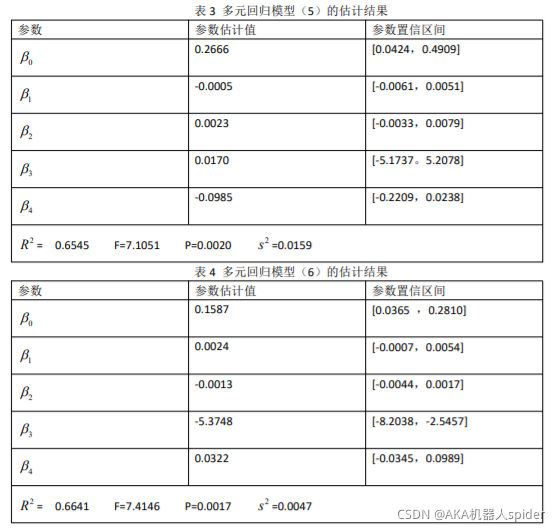
 问题四：

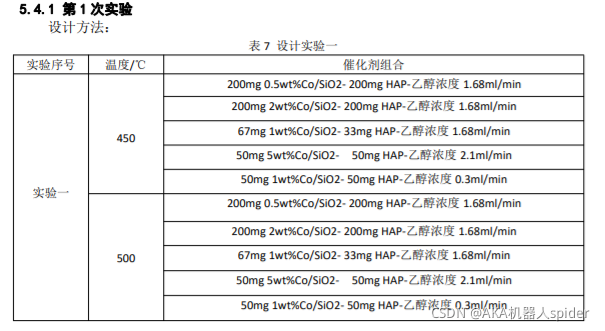
未完待续...

完整版包括附件已上传到资源里需要可自行下载：

https://download.csdn.net/download/Hdhdi/85468121

一、写好数模答卷的重要性
1.  评定参赛队的成绩好坏、高低，获奖级别，数模答卷，是唯一依据。
2. 答卷是竞赛活动的成绩结晶的书面形式。
3. 写好答卷的训练，是科技写作的一种基本训练。 
二、答卷的基本内容，需要重视的问题
1 评阅原则：  假设的合理性， 建模的创造性，结果的合理性，表述的清晰程度。 
2 答卷的文章结构
  0） 摘要
  1） 问题的叙述，问题的分析，背景的分析等，略 
  2） 模型的假设，符号说明（表）
  3）模型的建立（问题分析，公式推导，基本模型，最终或简化模型 等）  
  4） 模型的求解
    ▲ 计算方法设计或选择；
      算法设计或选择， 算法思想依据，步骤及实现，计算框图；所采用的软件名称；
    ▲ 引用或建立必要的数学命题和定理；
    ▲ 求解方案及流程 
  5） 结果表示、分析与检验，误差分析，模型检验……
  6） 模型评价，特点，优缺点，改进方法，推广…….
  7） 参考文献
  8） 附录
      计算框图
      详细图表
      ……
3  要重视的问题 
  0） 摘要。包括： a.模型的数学归类（在数学上属于什么类型）；b. 建模的思想（思路）；c . 算 法思想（求解思路）；d. 建模特点（模型优点，建模思想或方法，算法特点，结果检验，灵敏度分析，模型检验…….）；e. 主要结果（数值结果，结论）（回答题目所问的全部“问题”）
  ▲表述：准确、简明、条理清晰、合乎语法、字体工整漂亮；打印最好，但要求符合文章格式。务必认真校对。
  1） 问题重述。略
  2） 模型假设
     跟据全国组委会确定的评阅原则，基本假设的合理性很重要。
    （1）根据题目中条件作出假设
    （2）根据题目中要求作出假设
     关键性假设不能缺；假设要切合题意
  3） 模型的建立
    （1） 基本模型：
      1) 首先要有数学模型：数学公式、方案等
      2) 基本模型，要求 完整，正确，简明
    （2） 简化模型
      1） 要明确说明：简化思想，依据
      2） 简化后模型，尽可能完整给出
    （3） 模型要实用，有效，以解决问题有效为原则。
  数学建模面临的、要解决的是实际问题，不追求数学上：高（级）、深（刻）、难（度大）。
    u 能用初等方法解决的、就不用高级方法，
    u 能用简单方法解决的，就不用复杂方法，
    u 能用被更多人看懂、理解的方法，就不用只能少数人看懂、理解的方法。
    （4）鼓励创新，但要切实，不要离题搞标新立异
     数模创新可出现在
    ▲建模中，模型本身，简化的好方法、好策略等，
    ▲模型求解中
    ▲结果表示、分析、检验，模型检验
    ▲推广部分
    （5）在问题分析推导过程中，需要注意的问题：
    u 分析：中肯、确切
    u 术语：专业、内行；； 
    u 原理、依据：正确、明确,
    u 表述：简明，关键步骤要列出
    u 忌：外行话，专业术语不明确，表述混乱，冗长。
4． 模型求解
  （1） 需要建立数学命题时：
    命题叙述要符合数学命题的表述规范，尽可能论证严密。
  （2） 需要说明计算方法或算法的原理、思想、依据、步骤。若采用现有软件，说明采用此软件的理由，软件名称
  （3） 计算过程，中间结果可要可不要的，不要列出。
  （4） 设法算出合理的数值结果。
5． 结果分析、检验；模型检验及模型修正；结果表示
  （1） 最终数值结果的正确性或合理性是第一位的 ；
  （2） 对数值结果或模拟结果进行必要的检验。
        结果不正确、不合理、或误差大时，分析原因， 
        对算法、计算方法、或模型进行修正、改进；
  （3） 题目中要求回答的问题，数值结果，结论，须一一列出； 
  （4） 列数据问题：考虑是否需要列出多组数据，或额外数据对数据进行比较、分析，为各种方案的提出提供依据；
  （5） 结果表示：要集中，一目了然，直观，便于比较分析 
    ▲数值结果表示：精心设计表格；可能的话，用图形图表形式
    ▲求解方案，用图示更好 
  （6） 必要时对问题解答，作定性或规律性的讨论。最后结论要明确。
6．模型评价
    优点突出，缺点不回避。
    改变原题要求，重新建模可在此做。
    推广或改进方向时，不要玩弄新数学术语。
7．参考文献
8．附录
    详细的结果，详细的数据表格，可在此列出。但不要错，错的宁可不列。主要结果数据，应在正文中列出，不怕重复。   
    检查答卷的主要三点，把三关：
    n 模型的正确性、合理性、创新性
    n 结果的正确性、合理性
    n 文字表述清晰，分析精辟，摘要精彩
三、对分工执笔的同学的要求
四．关于写答卷前的思考和工作规划
    答卷需要回答哪几个问题――建模需要解决哪几个问题 
    问题以怎样的方式回答――结果以怎样的形式表示 
    每个问题要列出哪些关键数据――建模要计算哪些关键数据
    每个量，列出一组还是多组数――要计算一组还是多组数……
五．答卷要求的原理
    u 准确――科学性
    u 条理――逻辑性
    u 简洁――数学美
    u 创新――研究、应用目标之一，人才培养需要
    u 实用――建模。实际问题要求。
建模理念：
    1. 应用意识：要解决实际问题，结果、结论要符合实际；模型、方法、结果要易于理解，便于实际应用；站在应用者的立场上想问题，处理问题。
    2. 数学建模：用数学方法解决问题，要有数学模型；问题模型的数学抽象，方法有普适性、科学性，不局限于本具体问题的解决。
    3. 创新意识：建模有特点，更加合理、科学、有效、符合实际；更有普遍应用意义；不单纯为创新而创新。
 

⭐⭐⭐持续更新.....

⭐⭐⭐每天提醒自己，自己就是个菜鸡！

⭐⭐⭐如果对您有帮助留下的每一个点赞、收藏、关注是对菜鸡创作的最大鼓励❀

⭐⭐⭐有相关问题可以写在评论区，一起学习，一起进步。