【数据结构】复杂度(长期维护)

本篇博客主要是浅谈数据结构概念及时间复杂度，并做长期的维护更新，有需要借鉴即可。

一、初识数据结构

1.基础概念

数据结构(Data Structure) 是计算机存储、组织数据的方式，指相互之间存在一种或多种特定关系的数据元素的集合。简单来说，数据结构就是在内存中管理数据。

相关概念拓展：
算法(Algorithm) 就是定义良好的计算过程，他取一个或一组的值为输入，并产生出一个或一组值作为输出。简单来说算法就是一系列的计算步骤，用来将输入数据转化成输出结果。简单来说，算法就是在磁盘中管理数据。

在内存与磁盘中管理数据的区别：
在内存中，

• 数据存储速度比较快(相对磁盘而言)
• 属于带电存储类型

相对应的，在磁盘中，

• 数据存储速度比较慢(相对内存而言)
• 属于不带电存储类型。

思考：带电与不带电存储对存储的影响是什么？
答：存储寿命
如果是需要带电存储，那么就需要不断电，那么也就意味这文件内容不能永久性存储；相应的，如果可以脱离电量进行存储，那么就可以永久性存储在硬件中(这里不考虑硬件寿命问题)。

2.如何学好数据结构

• 画图
  
• 代码练习与思考
  

二、复杂度

1.复杂度

算法在编写成可执行程序后，运行时需要耗费时间资源和空间(内存)资源 。因此衡量一个算法的好坏，一般是从时间和空间两个维度来衡量的，即时间复杂度和空间复杂度。

元素个数的逐渐增大，复杂度的差异逐渐明显

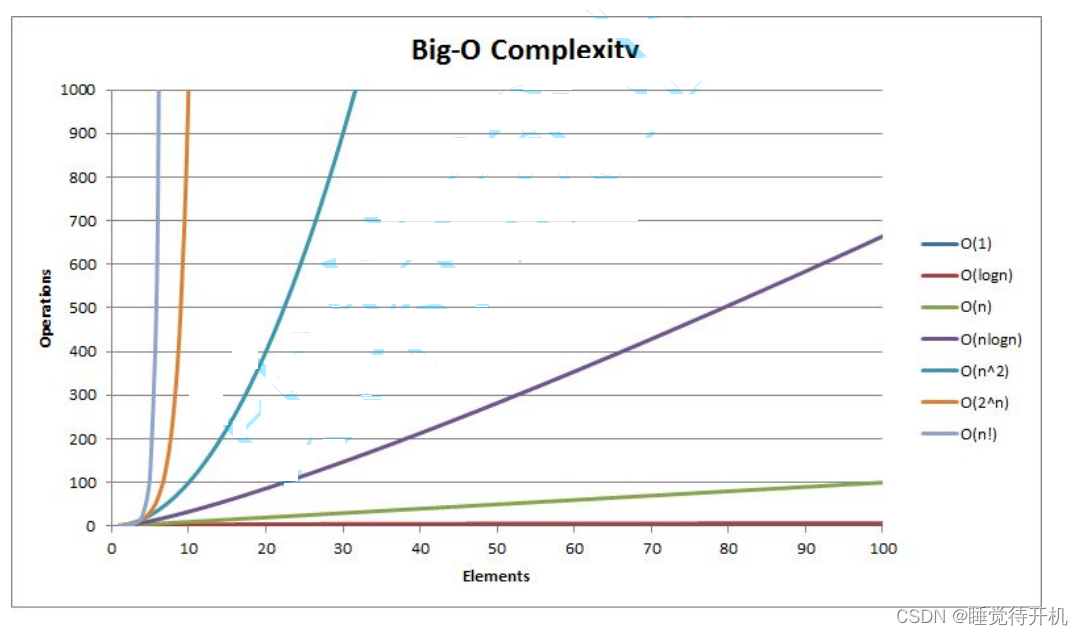
复杂度包括两个方面：

• 时间复杂度
• 空间复杂度

---

表示方法：
大O符号（Big O notation）：是用于描述函数渐进行为的数学符号。

1. 用常数1取代运行时间中的所有加法常数。
2. 在修改后的运行次数函数中，只保留最高阶项。
3. 如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。
4. 在实际中一般情况关注的是算法的最坏运行情况。

复杂度的意义何在？
用来衡量/决策比较某一种/多种实现方法的优劣
复杂度是准确的吗？
复杂度是粗略估计，对算法进行大致分“阶级”

2.时间复杂度

算法中的基本操作的执行次数，为算法的时间复杂度。

举例：

①有限数的时间复杂度

②函数的时间复杂度

注strchr:LINK

③二分查找时间复杂度

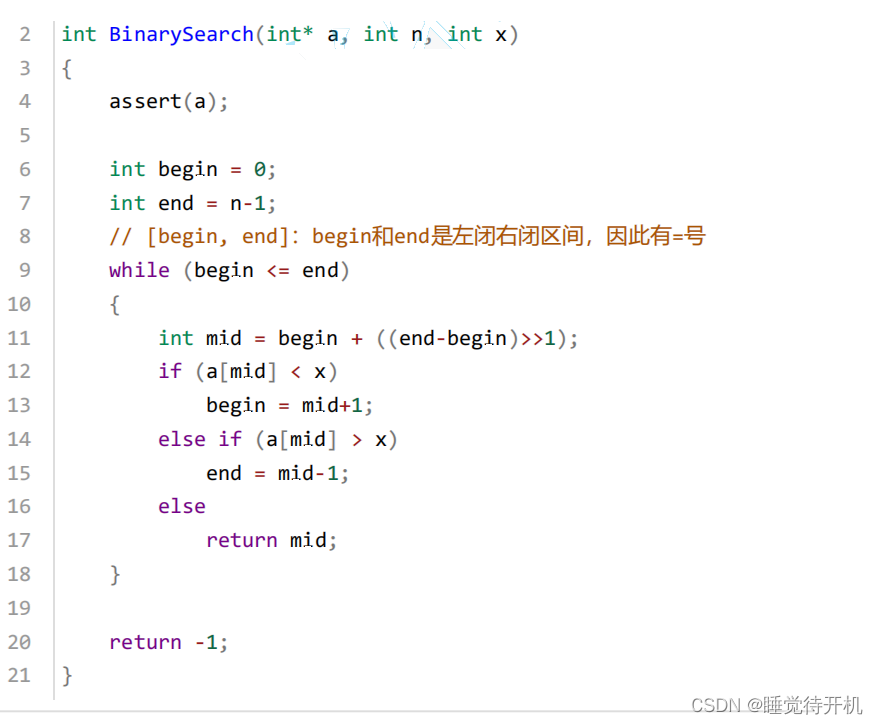
时间复杂度：O(logN)

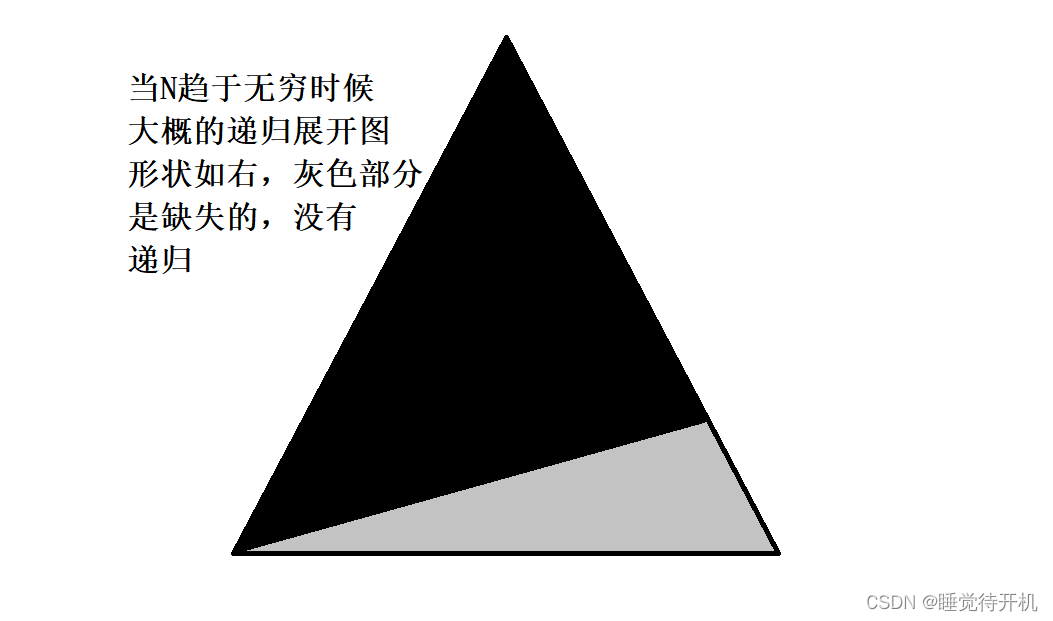
④递归

---

---

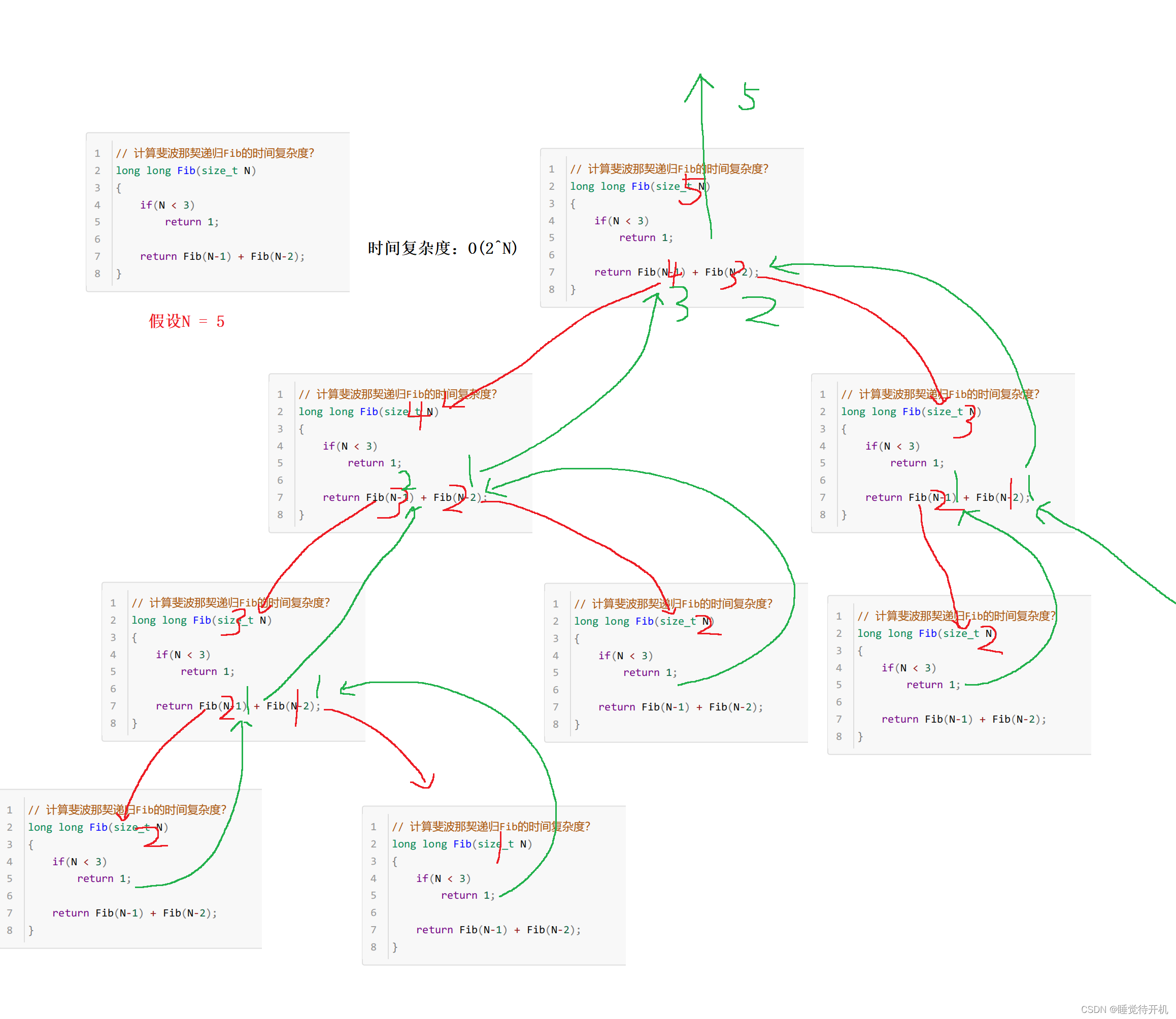
拓展练习题1：消失的数字

消失的数字:LINK

int missingNumber(int* nums, int numsSize){

// //思路二：先加起来然后减去，即可得到消失的数字
// int i = 0;
// int lose = 0;
// int sum = 0;
// //加上0到numsSize全部的数字
// for(i = 0;i<numsSize+1;i++)
// {
//     sum+=i;
// }
// //减去原数组0到numsSize的数字
// for(i = 0;i<numsSize;i++)
// {
//     sum-=nums[i];
// }
// //得到消失的数字
// lose = sum;
// return lose;

//思路三：异或操作
int i = 0;
int lose = 0;
//异或正常的数组
for(i = 0;i<numsSize+1;i++)
{
    lose^=i;
}
//异或原来的数组
for(i = 0;i<numsSize;i++)
{
    lose^=nums[i];
}
//返回
return lose;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

3.空间复杂度

为了实现某个功能额外开辟的空间。

需要注意的是：时间一去不复返，但是空间可以重复利用滴。

拓展练习题2：旋转数组

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>

//旋转数组
void printArray(int arr[],int length)
{
	for (int i = 0; i < length; i++)
	{
		printf("%d ", arr[i]);
	}
	printf("\n");
}

//1.暴力求解
void test1(int arr[],int length,int k)
{
	while (k--)
	{
		int temp = arr[length - 1];
		for (int i = length -1-1; i >= 0; i--)
		{
			arr[i+1] = arr[i];
		}
		arr[0] = temp;
	}
	printArray(arr, length);
}

void Swap(int arr[],int start,int end)
{
	while (start < end)
	{
		int temp = arr[start];
		arr[start] = arr[end];
		arr[end] = temp;
		start++;
		end--;
	}

}
//2.逆置法
void test2(int arr[], int length, int k)
{
	//1.首先逆置后半部分
	Swap(arr,length-k, length-1);
	printArray(arr, length);

	//2.其次逆置前半部分
	Swap(arr, 0, length - k - 1);
	printArray(arr, length);

	//3.整个数组进行逆置
	Swap(arr, 0, length - 1);

	printArray(arr, length);
}


//3.空间换时间方法
void test3(int arr[], int length, int k)
{
	//开辟空间
	int* temp = (int*)malloc(sizeof(int) * length);
	if (temp == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	
	//拷贝值到新数组中去
	for (int i = 0,j = k; i <= length - k - 1; i++,j++)
	{
		temp[j] = arr[i];
	}
	for (int i = length - k, j = 0; i <= length - 1; i++, j++)
	{
		temp[j] = arr[i];
	}

	//拷贝回去
	for (int i = 0; i < length; i++)
	{
		arr[i] = temp[i];
	}

	printArray(arr, length);
}

int main()
{
	int k = 3;
	int arr[] = { 1,2,3,4,5,6,7 };
	//test1(arr, sizeof(arr) / sizeof(int), k);
	//test2(arr, sizeof(arr) / sizeof(int), k);
	test3(arr, sizeof(arr) / sizeof(int), k);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98

拓展练习题③数组，二级指针

拓展练习题④移除元素

原题链接：LINK

//三条思路
//1.传统的覆盖
//2.开新数组
//3.双指针
int removeElement(int* nums, int numsSize, int val) {
    int i = 0;
    int p1 = 0;//探路者
    int p2 = 0;//守家者

    for(i = 0;i<numsSize;i++)
    {
        if(nums[p1]==val)
        {
            p1++;
        }
        else
        {
            nums[p2++] = nums[p1++];
        }
    }

    return p2;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

#if 1
/*
    解题思路:
        1. 设置一个变量count，用来记录nums中值等于val的元素的个数
        2. 遍历nums数组，对于每个元素进行如下操作：
            a. 如果num[i]等于val，说明值为val的元素出现了一次，count++
            b. 如果nums[i]不等于元素，将nums[i]往前搬移count个位置
                因为nums[i]元素之前出现过count个值等于val的元素，已经被删除了
                因此次数需要将nums[i]往前搬移
        3. 返回删除之后新数组中有效元素个数
        
    时间复杂度：O(N)   空间复杂度：O(1)
 */
int removeElement(int* nums, int numsSize, int val){
    int count = 0;
    for(int i = 0; i < numsSize; ++i)
    {
        if(nums[i] == val)
        {
            count++;
        }
        else
        {
            nums[i-count] = nums[i];
        }
    }


    return numsSize - count;
}
#endif

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

---

EOF