Stewart 平台的数学运动解析_斯图尔特平台原理

中文译本，原文：https://web.archive.org/web/20130506134518/http://www.wokinghamu3a.org.uk/Maths%20of%20the%20Stewart%20Platform%20v5.pdf

 

Stewart平台由2个刚性框架组成，由6条变长支臂连接。将底座作为参照系，以x、y、z为正交轴。顶部平台（以下均简写为平台）有它自己的正交坐标x '，y '， z '，相对于基座有6个自由度。平台坐标的原点可以由三个相对于基座的平移位移来定义，每个轴一个，三个角位移定义了平台相对于基座的方向，使用一组欧拉角来定义每个轴向的转角:

1、ψ（yaw，偏航角）为 z 轴方向上的旋转。

2、θ（pitch，俯仰角）为 y 轴方向上的旋转。

3、φ（roll，横滚角）为 x 轴方向上的旋转。

 

先只考虑第 ψ （yaw，偏航角）在 z 轴上的计算：

以上推导得旋转矩阵 Rz(ψ) 为

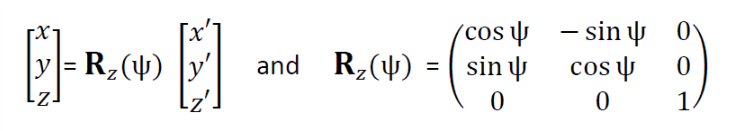
同理，可得 θ（俯仰）在 y 轴上的矩阵

φ 在 x 轴上的矩阵

结合整个旋转矩阵基于平台的运动就可得到

 

然后将矩阵置于Stewart平台中计算，支臂编号为 i

给出了锚点 Pi 相对于基准坐标系的坐标 qi 的方程

其中 T 为平移向量，给出平台框架原点相对于基准框架的位置线性位移，pi 为定义锚点相对于平台框架的坐标的向量。
同样，i 号支臂的长度公式为

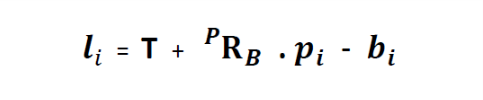
其中 bi 是向量，定义了下锚点Bi的坐标。这6个方程给出了实现平台所需位置和姿态的6条支臂的长度。
考虑正解运动学时，该表达式表示6个未知数中18个同时存在的非线性方程，表示平台的位置和姿态。在寻找这些方程的解方面已经做了大量的工作;在一般情况下，有40种可能的解决方案，尽管在实践中，这些解决方案中的许多并不实用。（说白了就是告诉你正解不合适）
 

后文似乎有个公式有些问题，等确认后再修改。待续...