【数据结构与算法】KMP算法

前言

 在C语言的strstr的实现过程中，所涉及的算法较为简单，或者说只是一个简单的思路而已，在字符串过长时，所涉及的算法复杂度过大，那有没有比较简单的算法呢？这里就涉及到了KMP——由三位大佬提出的，下面我们一起来了解吧！

一 .KMP的来历

 KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）。
巨佬1：D.E.Knuth
巨佬2：J.H.Morris
巨佬3：V.R.Pratt
图片：

简介：
 沃恩·普拉特（Vaughan Pratt） （出生于1944年4月12日）是 名誉教授 在 斯坦福大学 ，他是 计算机科学 。自1969年以来，普拉特（Pratt）对基础领域做出了一些贡献，例如 搜索算法, 排序算法 ， 和 素性测试 。最近，他的研究重点是对 并发系统 和 楚空间.百科全书 site:ewikizh.top

我浅浅地膜拜一下，因为从0到1创造出一个算法，那真是太牛了！
说明：在看这篇文章之前我推荐先看一下B站的视频（选择适合你的！）：
1.最浅显易懂的 KMP 算法讲解
2.KMP算法易懂版
3.有两个部分
第一：帮你把KMP算法学个通透！（理论篇）
第二：帮你把KMP算法学个通透！（求next数组代码篇）
在此基础上看这篇文章，可能收获会更大！

二.KMP解决的问题

1.引入

 由于暴力求解(l两层for循环)的算法时间复杂度为：o(mn),我们大概看一下下面的图表：

将mn最大化可以看成n^2,可知：字符串越长，求出结果所需时间也就越大，有更好的办法吗？sure！巨佬们，创造出了KMP算法，解决了这个问题。

2.定义的引入

1.字符串前缀

简单理解：
1.从开头字母到倒数第二个字母
2.开头字母依次接上第一个字母，第二字母……到倒数第二个字母，就像火车一样。
例：abc
前缀：a，ab

2.字符串后缀

简单理解：
1.从倒数第一个字母到正数第二个字母
2.从倒数第一个字母开始，依次接上倒数第二个字母，倒数第三个字母……正数第二个字母，这里字母要倒着接。
例:abc
后缀：c， bc
说明：a这是首字母也是末字母，不是前缀，也不是后缀。

3.最长相等前后缀

例1：aba
前缀：a，ab
后缀：a, ba
最长相等前后缀：a，最长相等前后缀长度是1
例2：aaaa
前缀：a，aa, aaa
后缀：a , aa, aaa
最长相等前后缀：aaa，最长相等前后缀长度是3
例3：a
前缀：无
后缀：无
最长相等前后缀：无，最长相等前后缀长度是0

3.核心思想

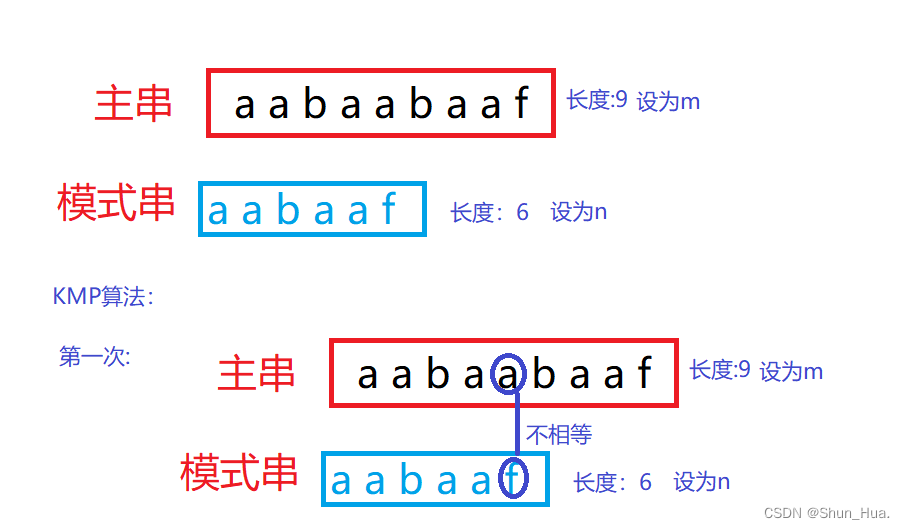
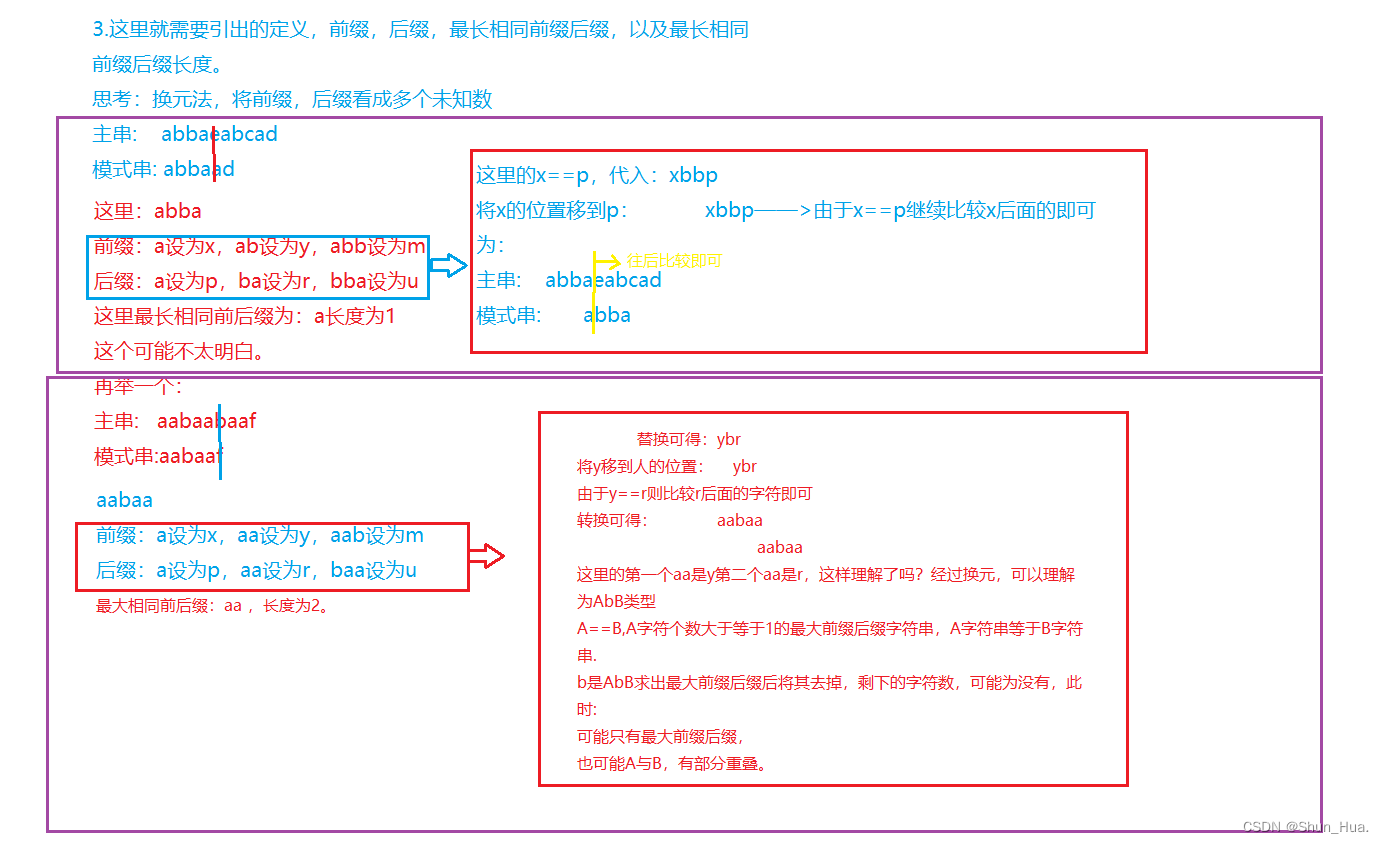
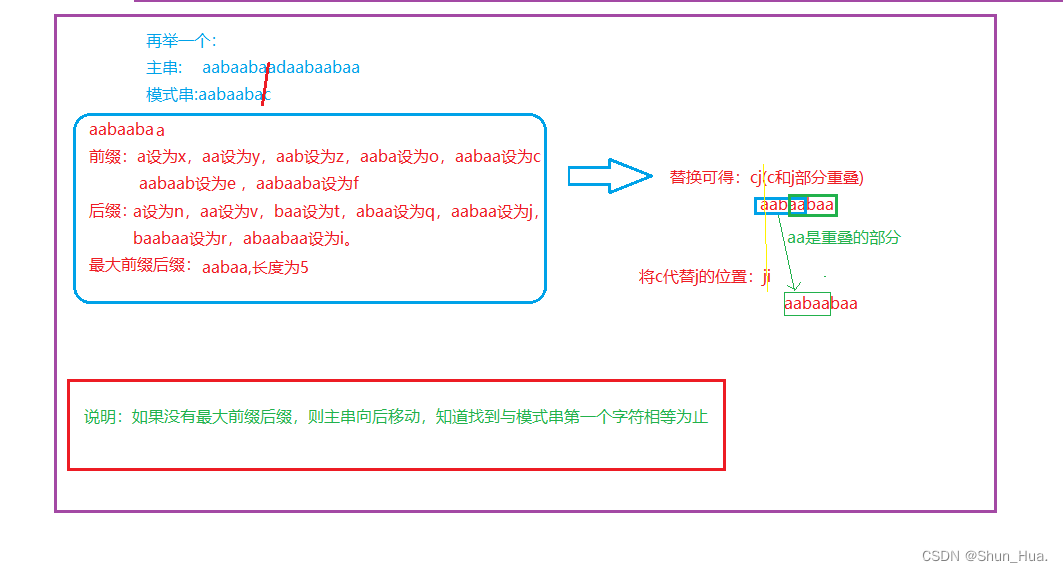
说明：我采用的是代码转换的思想，以及数学的换元法进行辅助理解。

三.next/prefix

1.next的含义

定义

 next是数组存放的是当发生比匹配的情况时：要进行的下一步操作，往往是当模式串的字符与对应的主串字符不匹配时，对应的下一步，不匹配的前一个字符跳到next下标对应的值或相似的运算。
 简单来说就是，下一步的该咋办，要写入next数组.

规律

一般是模式串下标和最长前缀后缀字符串的长度。
执行时间：当模式串的字符与主串字符串的对应字符不同时执行。
举例：

注意：
这里就充分利用了上一次比较的结果，使用上次比较的结果，进行下一步的比较。这里就方便了许多.
为什么方便呢？
换元思想就是最大前缀后缀的核心, 也就是方便的原因，这里求出的最大前缀后缀长度，刚好与下标的计算差1，也就是跳去的下标，刚好与主串的前一次不一样的字符对应，可以接着比较。这里就比较凑巧。

2.next的求取

说明：
人脑计算和机器计算不一样，人脑是把字符串依次拿出来比较，计算机可做不到这样，只能将下一步可能的操作全部记录下来，也就是next数组。
那如何进行快速计算呢？
这里的主要思想：回溯思想
说明：回溯思想，就跟游击战的意思差不多，打的过就打，打不过就走。

1.准备工作

图解：

框架：

void get_next(char arr1[], int next[], int len)
{
	next[0] = 0;//第一个字符为0，不管字符串的长度多大。
	int i = 0;//最开始的下标
	int j = 1;//最开始的字符串大于1的模式串的下标
	for (j = 1; j > len; j++)
	{
		while (arr1[i]!=arr1[j]&&i>0)
		{
			i = arr1[i - 1];
		}
		if (arr1[i] == arr1[j])
		{
			i++;
		}
		next[j] = i;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

2.思路和图解

4.应用

1.字符串中找模式串，以及类似的问题。（strstr这个函数就是找模式串的函数）

• 贴一份KMP的模版

vector<int> kmp(string& text,string& pattern)
{
    //求next数组
    int tsz = text.size(),psz = pattern.size();
    vector<int> next(psz);
    int index = 0;
    for(int i = 1; i < psz; i++)
    {
        char ch = pattern[i];
        while(index && ch != pattern[index])
        {
            //进行回退找最长匹配串与之匹配
            index = next[index-1];
        }
        if(ch == pattern[index])
            index++;
        next[i] = index;
    }
    vector<int> ans;
    //求子串的起始位置。
    index = 0;
    for(int i = 0; i < tsz; i++)
    {
        char ch = text[i];
        while(index && ch != pattern[index])
        {
            index = next[index-1];
        }
        if(ch == pattern[index])
            index++;
        
        if(index == psz)
        {
            //说明找到子串了,记录下标并进行回退
            ans.push_back(i + 1 - psz);
            index = next[index - 1];
        }
    }
    return ans;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

• 练习题：

1. 3008. 找出数组中的美丽下标 II

• 说明：KMP是一个很不错的算法，能将字符串匹配缩短到线性O(m + n)，关键就在于，将前缀的信息记录，匹配失败时可快速找到下一个可能匹配的字符子串。