二叉排序树详解

二叉排序树详解

摘要：本篇笔记专门介绍二叉排序树，重点讲解了二叉排序树的特性，以及二叉排序树各方面的基本实现。

1.二叉排序树简介

  二叉排序树又称为二叉搜索树，是一种重要的数据结构，需要注意的是，在使用二分搜索中，搜索数组中每一个数字的函数调用栈重叠起来，就是一个平衡的或者说是接近平衡的二叉排序树，也就是说使用有序数组进行二分搜索实际上和在一个二叉排序树搜索一个节点干的事情是一样的。并且，对于一棵二叉排序树的深度优先中序遍历结果，就是一个有序的数组。二叉排序树首先要求该树是一棵二叉树，之后要求在这棵树中，所有子树的根节点的左子树上的节点值或者说是权重要均小于(或大于)根节点，而右子树上的所有节点值或者说是权重均大于(或小于)根节点。如图所示：

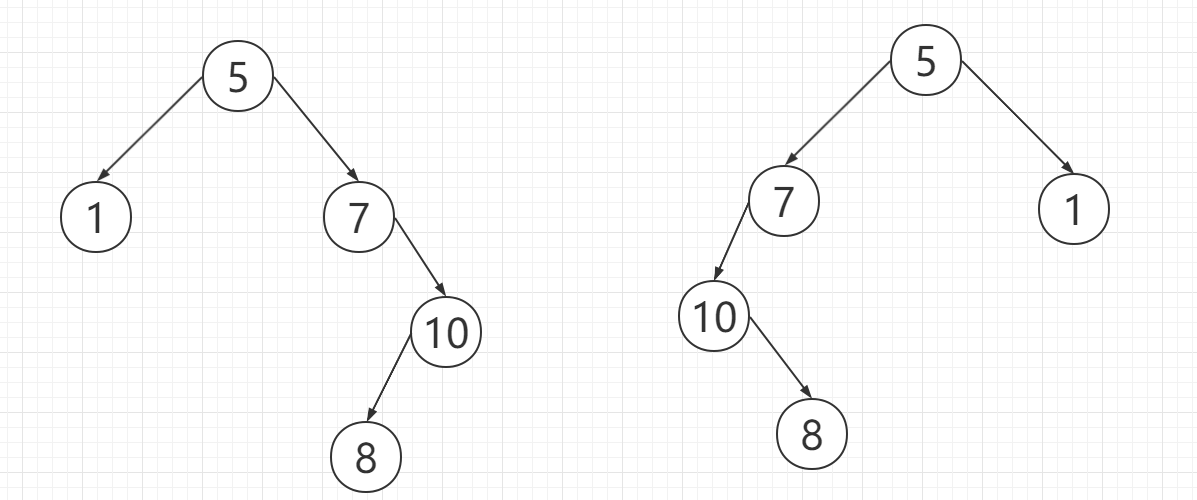
  二者均为二叉排序树，其中的左右的大小关系根据具体情况而定。

2.二叉排序树的实现

2.1.二叉排序树的节点实现

  二叉排序树的节点和普通树的节点没有差异，只是整棵树在生成的时候有所限制，因此不再画图介绍，我们在IDE中直接创建TreeNode.java文件，代表树的节点类，如图所示：

  之后我们开始书写代码，在树的节点类中，我们需要创建的字段分别为leftChildNode，rightChildNode以及value，我们将他们声明为私有类型，如图所示：

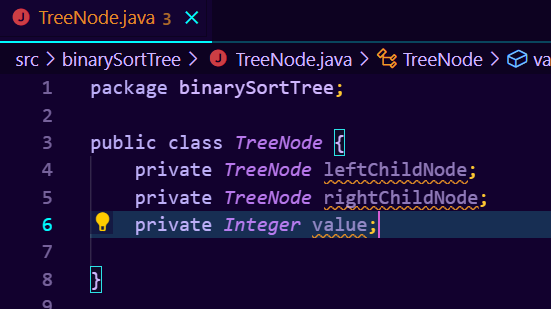
  我们为其编写一个构造器，以便于节点对象初始化的时候就将这些数据进行赋值，如图所示：

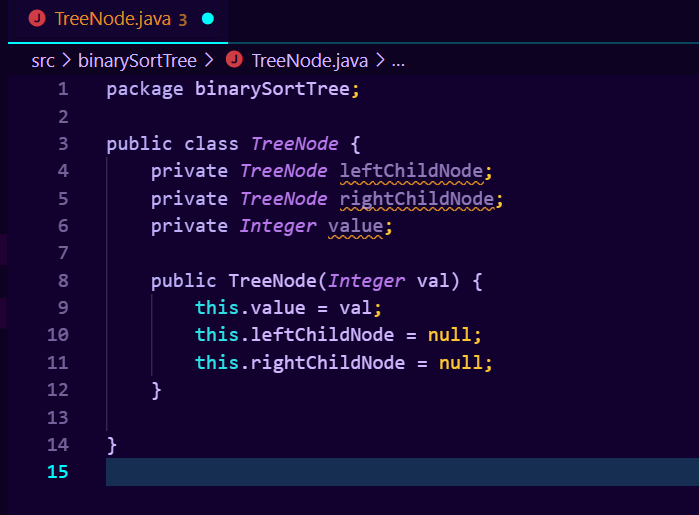
  之后我们为其所有字符生成访问器和修改器，方法简单，不再赘述，生成后如图所示：

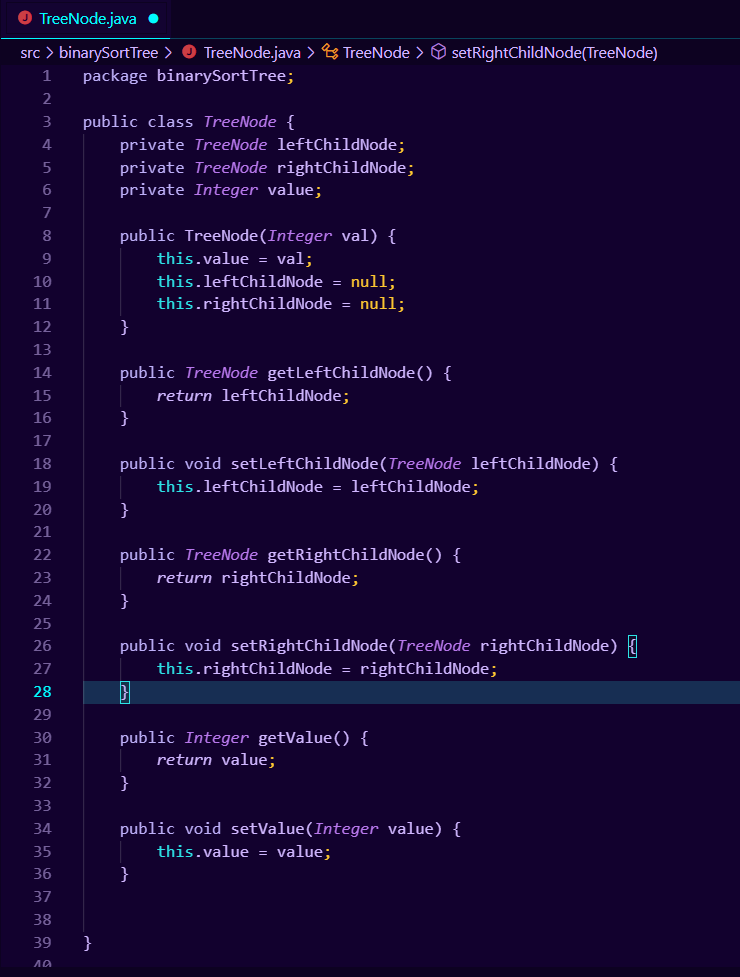
  在此附上源码：

package binarySortTree;

public class TreeNode {
    private TreeNode leftChildNode;
    private TreeNode rightChildNode;
    private Integer value;

    public TreeNode(Integer val) {
        this.value = val;
        this.leftChildNode = null;
        this.rightChildNode = null;
    }

    public TreeNode getLeftChildNode() {
        return leftChildNode;
    }

    public void setLeftChildNode(TreeNode leftChildNode) {
        this.leftChildNode = leftChildNode;
    }

    public TreeNode getRightChildNode() {
        return rightChildNode;
    }

    public void setRightChildNode(TreeNode rightChildNode) {
        this.rightChildNode = rightChildNode;
    }

    public Integer getValue() {
        return value;
    }

    public void setValue(Integer value) {
        this.value = value;
    }
    

}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

2.2.二叉排序树的管理类实现

  二叉排序树的管理类实际上就是二叉排序树类，在这个类中定义了二叉排序树的存储结构，以及对于二叉排序树的各种方法，因此关于二叉排序树的生成，节点添加，节点修改，节点删除，节点搜索等各种方法都会在此定义。为此，我们特意新建一个BinarySortTree.java来存储这个管理类，如图所示：

2.2.1.二叉排序树的结构定义

  在管理类中，我们通常会定义一个指针字段，用于指向实体结构的首索引节点，如在链表中我们会定义一个head节点，而在二叉排序树中我们也会定义一个root节点，在之后的各种生成操作中，我们都会以这个节点为首索引节点，在这个节点上进行扩充，简而言之，我们使用这个节点来表示整棵树结构，实际上它并不是一棵树，但是它是我们访问这棵树的入口，因此我们在逻辑上认为它就是这棵树逻辑上的实体，它的定义并不难，一个字段即可，如图所示：

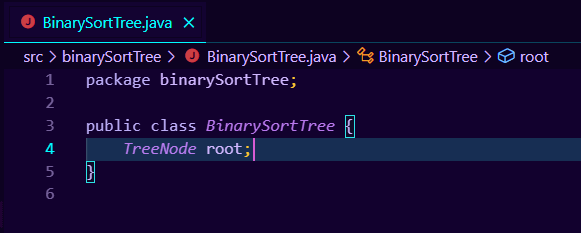
  然而，真正困难的方法才刚要到来，接下来，我们研究二叉排序树的插入方法。

2.2.2.二叉排序树的插入方法定义

  首先我们使用画图的方式来描绘一下二叉排序树的插入过程，如图，我们要在一棵空的二叉排序树中插入一个数组6,2,7,4,0,3,1,5，如图所示：

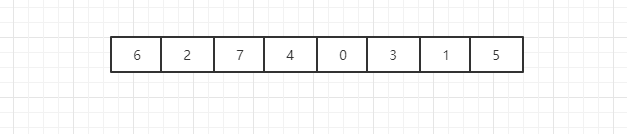
  首先我们插入第一个元素6，此时二叉排序树中还没有任何一个节点，因此我们应该新建一个节点，并将6存储进去，并将6认定为根节点，如图所示：

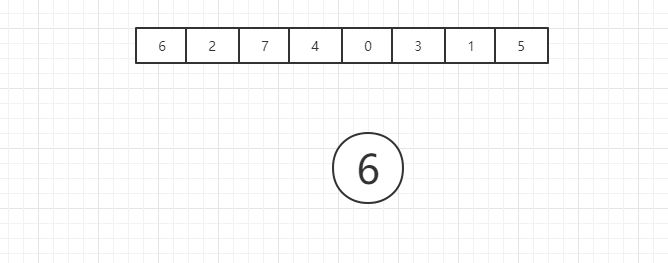
  之后我们插入第二个元素2，此时二叉排序树已经不是一个空树了，因此我们需要首先找到适合它的位置，我们将2和6进行对比，判断谁大谁小，我们发现2更小，因此2应该被插入在6的左子树中，之后我们将2和根节点6的左子树进行对比，发现6的左子树是空的，因此这时我们将2存放在6的左子树根节点位置，如图所示：

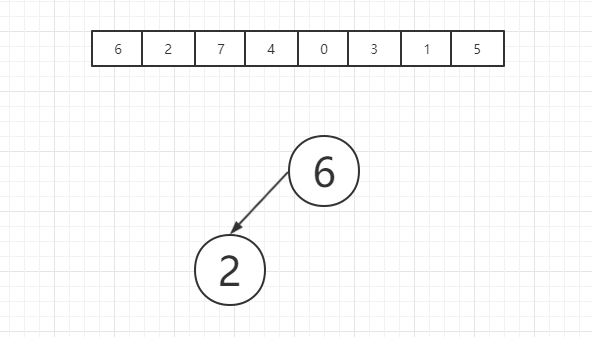
  之后是元素7,7显然大于6，因此我们要将7放在6的右子树中，经过探寻我们发现6的右子树根节点也是空的，因此我们需要将7放在右子树的根节点上，如图所示：

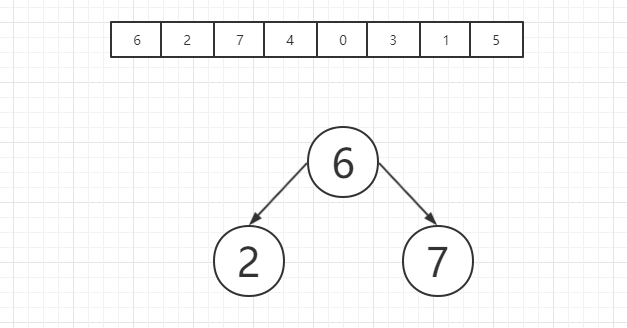
  之后是元素4，我们首先将4和6对比，发现4是小于6的，因此4应该位于6的左子树上，之后我们将4和6的左子树根节点进行对比，发现4是大于2的，因此4应该被放在2的右子树上，而2的右子树为空，因此4直接被放置在2的右子树根节点上，如图所示：

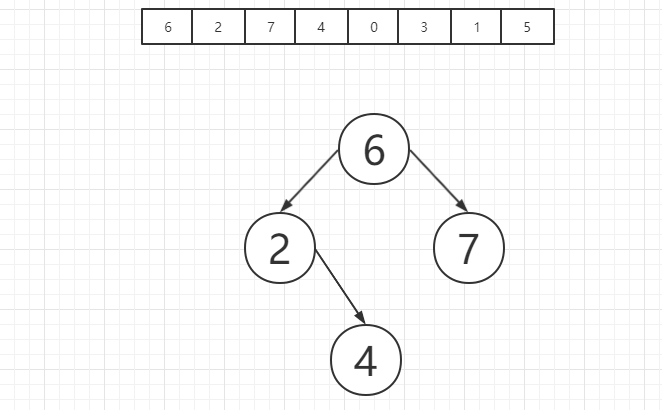
  之后是元素0，首先我们将0和元素6进行对比，发现0是小于元素6的，因此应该被放置在6的左子树上，之后我们将0和6的左子树根节点进行对比，发现其小于2，因此0应该被放置在2的左子树上，这时我们发现0是小于2的，因此0应该被放置在2的左子树上，同时我们发现2的左子树为空，因此我们将0放置在2的左子树根节点上，如图所示：

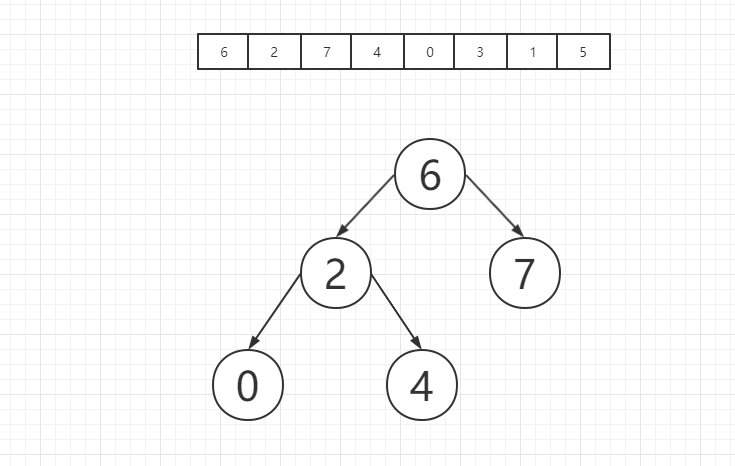
  之后是元素3，我们发现元素3是小于6的，因此3应该被放置在6的左子树上，而这时我们就开始研究6的左子树，3大于2，因此3应该被放置在2的右子树上，这时我们开始研究2的右子树，而3是小于2的右子树根节点4的，因此3应该放置在4的左子树上，我们发现4的左子树为空，因此我们将3放置在4的左子树根节点上，如图所示：

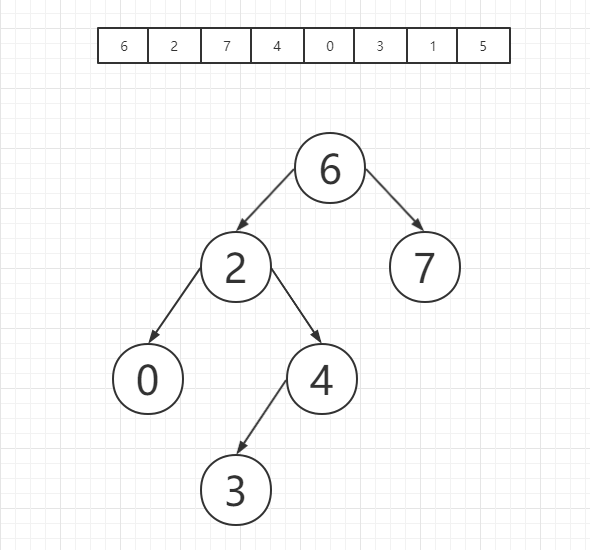
  之后是元素1，首先我们将1和6进行对比，发现1是小于6的，因此1应该被放置在6的左子树上，而1又小于2，因此应该被放置在2的左子树上，而1又大于0，因此应该被放置在0的右子树上，0的右子树为空，因此1应该被放置在0的右子树根节点上，如图所示：

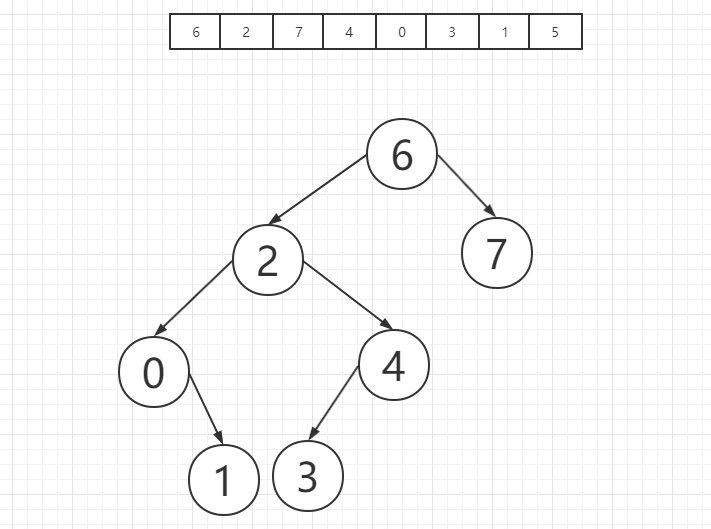
  之后我们研究最后一个元素5,5小于根节点6，因此我们应该将5放置在6的左子树上，而5大于2，因此我们应该将5放置在2的右子树上，5大于4，因此5应该被放置在4的右子树上，4的右子树为空，因此我们将5放置在4的右子树根节点上，如图所示：

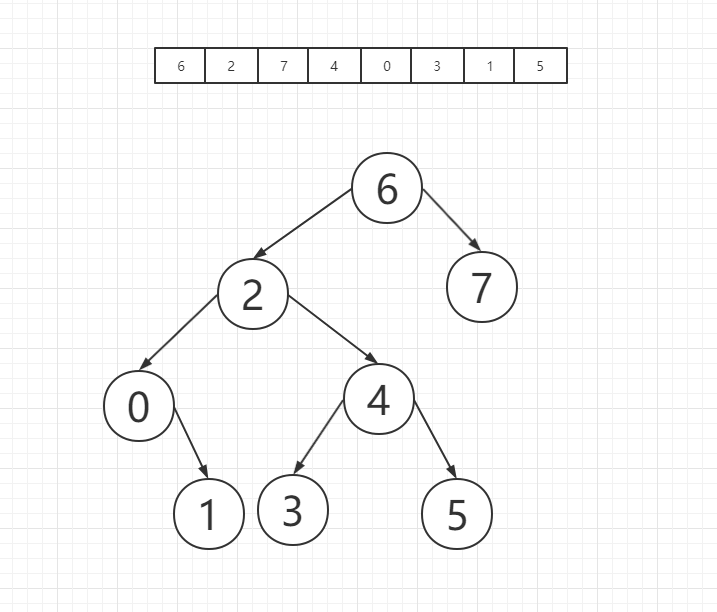
  至此这个二叉排序树宣布构造完毕，经过这个步骤，我们可以分析出二叉排序树的插入规则：新的节点只能被插入在一个叶子节点之下，这个插入过程实际上是新节点在和不同规模的子树的根节点进行比较之后，被放置在了一个最小的或者是次最小的子树之下，并一定会形成一个新的最小规模子树，新的节点一定会作为一个新子树的根节点，而不是顶替一个已有子树的根节点。因此我们总结出来了插入的规律：

1.检查该二差排序树是否为空，如果为空，则将新节点指定为根节点，否则将新节点与根节点进行比较；
2.根据比较结果，确定新节点应该插入根节点的左子树还是右子树，之后我们将应该被插入的左右子树作为新的研究对象，重复1过程
1
2

  现在我们来书写代码，首先我们书写一个普通的实现方式，代码如图所示：

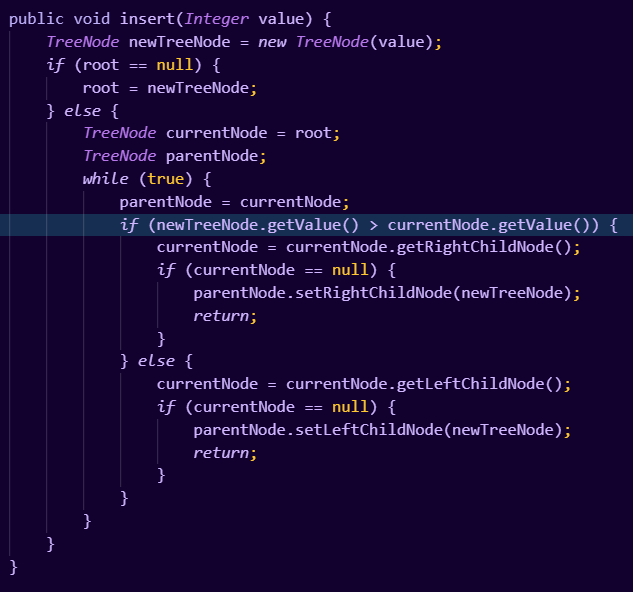
  我们在TreeNode类中重写一个toString方法，用来测试一下这个插入方法：

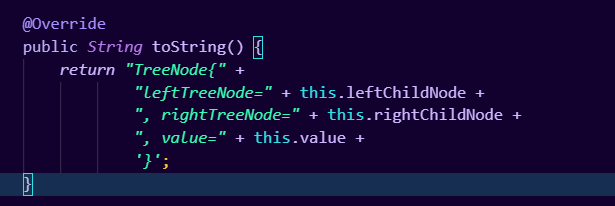
  书写测试代码如下：

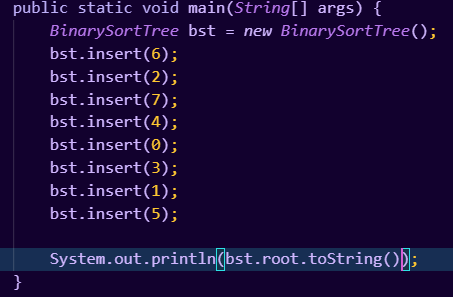
  获取输出结果如下：

//整理如下：
TreeNode{
    leftTreeNode=TreeNode{
        leftTreeNode=TreeNode{
            leftTreeNode=null, 
            rightTreeNode=TreeNode{
                leftTreeNode=null, 
                rightTreeNode=null, 
                value=1
            }, 
            value=0
        }, 
        rightTreeNode=TreeNode{
            leftTreeNode=TreeNode{
                leftTreeNode=null, 
                rightTreeNode=null, 
                value=3
            }, 
            rightTreeNode=TreeNode{
                leftTreeNode=null, 
                rightTreeNode=null, 
                value=5
            }, 
            value=4
        }, 
        value=2
    }, 
    rightTreeNode=TreeNode{
        leftTreeNode=null, 
        rightTreeNode=null, 
        value=7
    }, 
    value=6
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

  经验证发现这个输出结果是正确的，接下来我们分析代码：

public void insert(Integer value) {
        TreeNode newTreeNode = new TreeNode(value);//首先建立一个新节点，代表即将要插入的节点
        if (root == null) {//检查根结点，如果根结点为null的话，我们直接将新节点赋值给根节点
            root = newTreeNode;
        } else {//否则我们将进行普通的插入操作
            TreeNode currentNode = root;//设置一个心指针指向当前结构的根节点
            TreeNode parentNode;//为了便于插入，我们专门设置一个父节点，让它一直指向当前指针的父节点
            while (true) {//让循环一直进行下去
                parentNode = currentNode;//父节点保存当前节点值
                if (newTreeNode.getValue() > currentNode.getValue()) {//如果新节点的值大于当前节点，那么我们进行如下操作
                    currentNode = currentNode.getRightChildNode();//如果新节点的值大于当前节点，那我们首先要让当前指针指更新，指向它的右子树
                    if (currentNode == null) {//如果右子树为空，那么说明此时有供新节点插入的空位，那么我们进行插入
                        parentNode.setRightChildNode(newTreeNode);//因为当前指针已经更新，但是父节点保存了它更新之前的值，此时父节点指向的就是当前指针的上一个节点，因此直接让父节点指针的右子树等于新节点即可
                        return;//插入一个之后立即返回
                    }
                    //如果右子树不为空，则什么也不做，让循环继续推移
                } else {//如果新节点的值不大于当前节点，我们则进行如下操作
                    currentNode = currentNode.getLeftChildNode();//我们将让当前指针更新为自己的左孩子节点
                    if (currentNode == null) {//同理，此时我们应该进行插入操作
                        parentNode.setLeftChildNode(newTreeNode);//因为父节点已经保存了之前的指向，我们直接让父节点的做孩子节点为新节点
                        return;
                    }
                }
            }
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

  对于这个方法我又一个小小的优化方案，可以去掉父节点指针的使用：

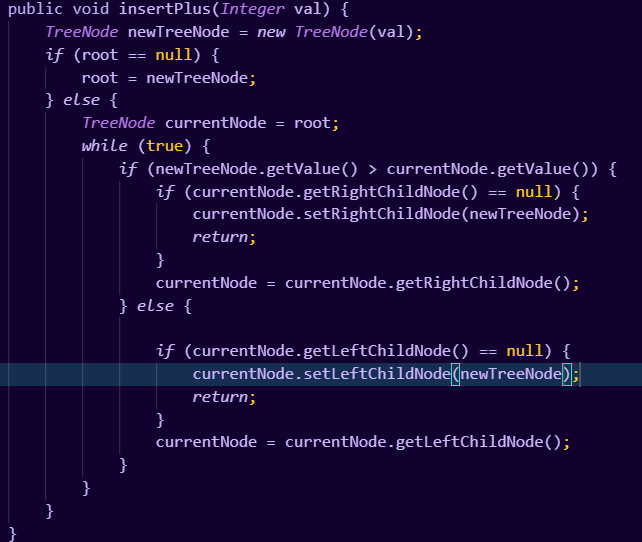
  现在让我们修改测试代码如下：

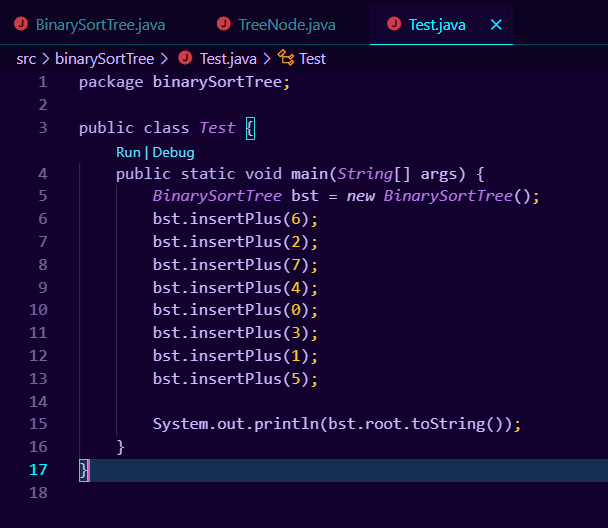
  我们运行查看输出如下：

TreeNode{
    leftTreeNode=TreeNode{
        leftTreeNode=TreeNode{
            leftTreeNode=null, 
            rightTreeNode=TreeNode{
                leftTreeNode=null, 
                rightTreeNode=null, 
                value=1
            }, 
            value=0
        }, 
        rightTreeNode=TreeNode{
            leftTreeNode=TreeNode{
                leftTreeNode=null, 
                rightTreeNode=null, 
                value=3
            }, 
            rightTreeNode=TreeNode{
                leftTreeNode=null, 
                rightTreeNode=null, 
                value=5
            }, 
            value=4
        }, 
        value=2
    }, 
    rightTreeNode=TreeNode{
        leftTreeNode=null, 
        rightTreeNode=null, 
        value=7
    }, value=6
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

  我们可以发现其结果是和之前的方法输出一致的。除去普通的插入方法外，我们还可以使用一种递归的方法，首先因为这个插入过程就是一个递归插入的过程，实际上我们做的事情是：拿到新节点之后，先将其放在最大的树中进行比较，我们让它和根节点进行比较，如果其小于根节点，这时我们查看根节点是否拥有左子树，并将新节点放在根节点的左子树上进行比较，此时我们是与左子树的根节点进行了比较，我们将眼界缩小到了一棵子树，然后我们重复这个过程，因此这也是一个递归的过程，我们可以书写这样的递归方法来解决这个问题：

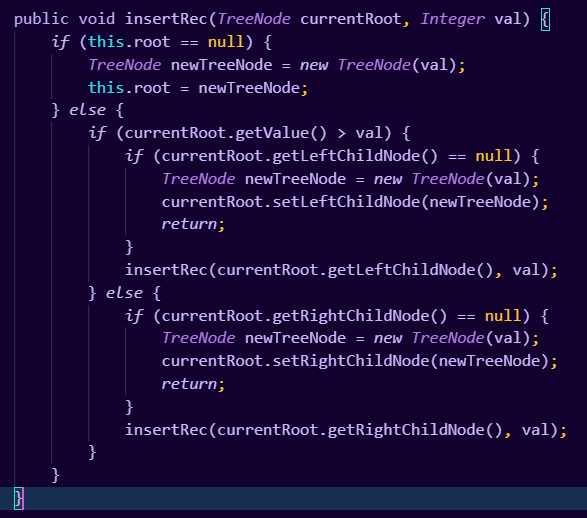
  验证输出为：

TreeNode{
    leftTreeNode=TreeNode{
        leftTreeNode=TreeNode{
            leftTreeNode=null, 
            rightTreeNode=TreeNode{
                leftTreeNode=null, 
                rightTreeNode=null, 
                value=1
            }, value=0
        }, rightTreeNode=TreeNode{
            leftTreeNode=TreeNode{
                leftTreeNode=null, 
                rightTreeNode=null, 
                value=3
            }, 
            rightTreeNode=TreeNode{
                leftTreeNode=null, 
                rightTreeNode=null, 
                value=5
            }, 
            value=4
        }, 
        value=2
    }, 
    rightTreeNode=TreeNode{
        leftTreeNode=null, 
        rightTreeNode=null, 
        value=7
    }, 
    value=6
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

  验证正确。

  代码如下：

public void insertRec(TreeNode currentRoot, Integer val) {
        if (this.root == null) {//如果结构根节点为null，那么先为其赋予一个实体节点
            TreeNode newTreeNode = new TreeNode(val);
            this.root = newTreeNode;
        } else {
            if (currentRoot.getValue() > val) {//如果即将插入的值小于当前根节点
                if (currentRoot.getLeftChildNode() == null) {//那么这个新节点铁定要往它的左子树上放，我们先看看它的左子树是否为空，是否能直接放
                    TreeNode newTreeNode = new TreeNode(val);//如果为空说明此时我们可以直接放，那么我们就直接生成一个新节点，然后直接往里放
                    currentRoot.setLeftChildNode(newTreeNode);//这里就是放入的过程
                    return;
                }
                insertRec(currentRoot.getLeftChildNode(), val);//否则我们继续研究其左子树，将插入范围缩小到当前节点的左子树上，在下一层递归，将以当前根节点的左子树作为研究对象
            } else {
                if (currentRoot.getRightChildNode() == null) {
                    TreeNode newTreeNode = new TreeNode(val);
                    currentRoot.setRightChildNode(newTreeNode);
                    return;
                }
                insertRec(currentRoot.getRightChildNode(), val);
            }
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

3.二叉排序树的中序遍历

  二叉树的深度优先中序遍历，对于一棵子树的遍历，是先检索左孩子节点，然后在检索根节点，之后再检索右孩子节点的，对于一棵比较大的树，它会递归的检索左子树，左子树检索完毕之后检索根节点，之后再递归的检索右子树，这个检索过程使得二叉排序树的深度优先中序遍历结果，是一个有序的排列，接下来我们写一下二叉排序树的中序遍历：

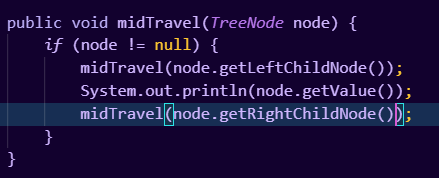
  使用递归的方法并不难写，接下来让我们调用看看我们构建的二叉排序树使用中序遍历输出出来是否是一个有序的排列：

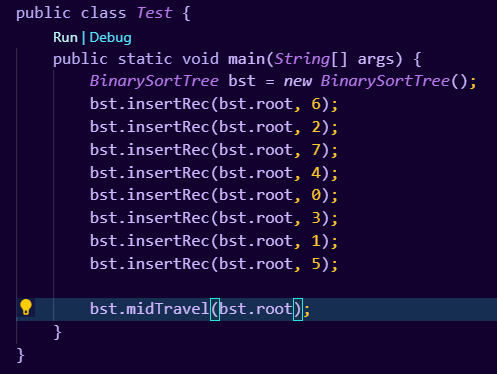
  结果如下图所示，很显然我们输出了一个有序排列：

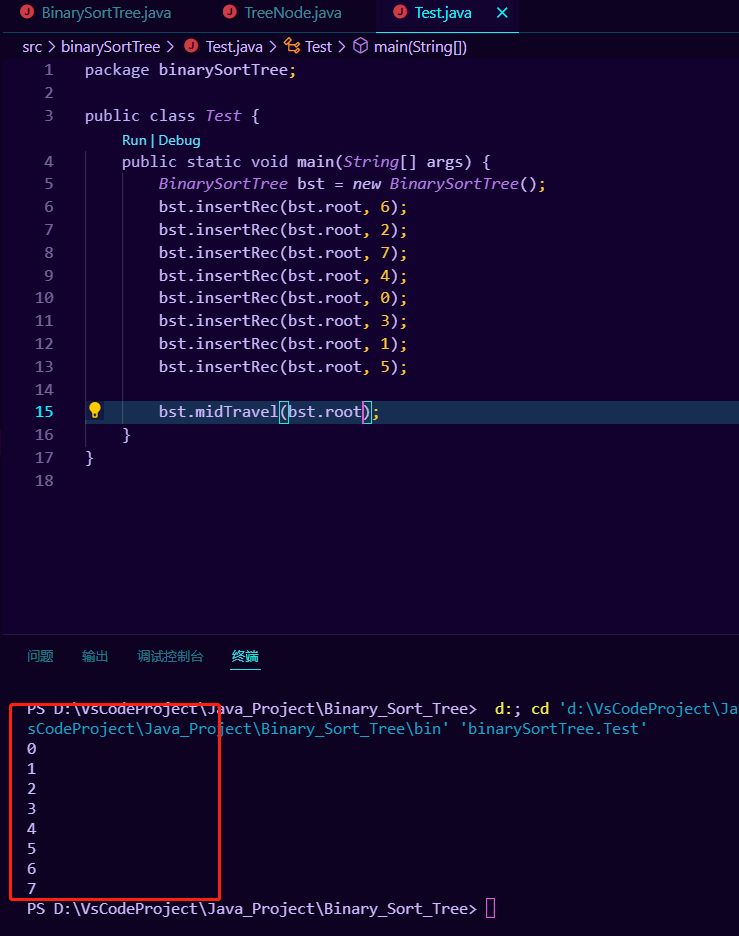
4.二叉排序树的节点查找

  在二叉排序树中进行指定值的节点查找非常简便，这个查找过程实际上就是一个二分搜索的过程，我们首先创建一个遍历指针，让这个指针指向排序树的根节点，如果根节点值等于我们想要查找的值，那么我们就直接进行返回操作即可，如果不等于，那么根节点必定大于或者小于我们要查找的值，此时我们根据具体情况在根节点的左子树或者右子树中继续查询，这里是一个递归过程，算法比较简单，因此不再深入研究，直接附上代码。

public TreeNode search(TreeNode node, int value){
        if(node == null){
            return null;
        }
        if(node.getValue()>value){
            if(node.getLeftTreeNode() == null)
                return null;
            return search(node.getLeftTreeNode(),value);
        }else if(node.getValue()<value){
            if(node.getRightTreeNode() == null)
                return null;
            return search(node.getRightTreeNode(),value);
        }else{
            return node;
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

5.二叉排序树的节点删除

  关于这个问题，实际上比较复杂，为了避免增大篇幅，我另起一篇笔记来记录这个知识点，点击链接查看。