python基于GCN（图卷积神经网络模型）和LSTM（长短期记忆神经网络模型）开发构建污染物时间序列预测模型_gcn-lstm

在以往的时间序列预测建模中广泛使用的是回归类算法模型和RNN类的算法模型，相对来说技术栈会更稳定一些，最近有一个实际业务场景的需求，在建模的过程中要综合考虑其余点位的影响依赖，这时候我想到了之前做过的交通流量和速度预测相关的项目，在那里采用的就是图相关的算法模型，所以这里也想对标来开发。

GCN（Graph Convolutional Network）是一种用于处理图结构数据的卷积神经网络模型。它的构建原理是基于图卷积操作，通过在图上进行局部的卷积运算来提取节点的特征表示。

具体来说，GCN通过邻居节点的信息聚合来更新每个节点的表示。GCN的每一层都可以表示为以下的公式：

H^{(l+1)} = σ(D^{-0.5}AD^{-0.5}H^{(l)}W^{(l)})

其中，H^{(l)}表示第l层的节点表示矩阵，A表示节点之间的邻接矩阵，D是度矩阵，W^{(l)}表示第l层的权重矩阵，σ表示激活函数。

GCN的优点主要体现在以下几个方面：

1. 考虑了节点的邻居信息：GCN通过聚合节点的邻居信息来更新节点的表示，能够捕捉到节点的局部结构信息，适用于处理图结构数据。
2. 具有共享权重的卷积：GCN通过共享权重矩阵来进行卷积操作，减少了需要学习的参数数量，降低了模型的复杂度。
3. 良好的泛化能力：GCN能够将节点的特征向量传递给邻居节点，从而在整个图上进行信息传播，有助于节点的特征表示学习。

然而，GCN也存在一些缺点：

1. 无法处理动态图：GCN对于静态图结构的处理效果较好，但对于动态图的处理存在一定的困难，因为动态图的结构会随着时间的推移而变化。
2. 局部邻居信息的限制：GCN只考虑节点的一阶邻居信息，对于高阶邻居信息的利用能力有限。
3. 对大规模图的计算开销较大：GCN的计算复杂度与图的规模相关，对于大规模图的处理需要较高的计算资源。

GCN作为一种处理图结构数据的卷积神经网络模型，具有考虑邻居信息、共享权重、泛化能力强等优点，但对动态图的处理存在限制，并且对大规模图的计算开销较大。

LSTM（Long Short-Term Memory）是一种用于处理序列数据的循环神经网络模型。它的构建原理是通过引入门控机制来解决传统RNN存在的梯度消失和梯度爆炸问题，从而能够更好地捕捉长期依赖关系。

具体来说，LSTM通过三个门控单元（输入门、遗忘门和输出门）来控制信息的流动和记忆的更新。它的计算过程可以表示为以下公式：

输入门：i_t = σ(W_{xi}x_t + W_{hi}h_{t-1} + b_i)
遗忘门：f_t = σ(W_{xf}x_t + W_{hf}h_{t-1} + b_f)
输出门：o_t = σ(W_{xo}x_t + W_{ho}h_{t-1} + b_o)
新的记忆：\tilde{c}t = tanh(W{xc}x_t + W_{hc}h_{t-1} + b_c)
细胞状态更新：c_t = f_t \odot c_{t-1} + i_t \odot \tilde{c}_t
隐藏状态更新：h_t = o_t \odot tanh(c_t)

其中，i_t、f_t和o_t分别表示输入门、遗忘门和输出门的输出，\tilde{c}_t表示新的记忆，c_t表示细胞状态，h_t表示隐藏状态，x_t表示当前时刻的输入。

LSTM的优点主要体现在以下几个方面：

1. 解决了梯度消失和梯度爆炸问题：通过门控机制，LSTM能够有效地捕捉长期依赖关系，解决了传统RNN在处理长序列时产生的梯度问题。
2. 长期记忆能力强：LSTM能够在细胞状态中长期存储信息，有助于模型记住对当前任务有用的信息。
3. 能够处理不定长的序列：LSTM可以处理不定长的序列数据，适用于多种应用场景，如自然语言处理、语音识别等。

然而，LSTM也存在一些缺点：

1. 计算复杂度较高：LSTM中引入了多个门控单元和记忆单元，导致模型的计算复杂度较高，对计算资源要求较大。
2. 可能存在过拟合：LSTM的参数数量较多，模型容易过拟合，需要采取一些正则化方法来缓解这个问题。
3. 难以并行化：LSTM的计算过程涉及到门控单元的计算，导致模型难以进行有效的并行化，限制了其在大规模数据上的应用。

LSTM作为一种用于处理序列数据的循环神经网络模型，具有解决梯度问题、长期记忆能力强等优点，但计算复杂度较高、难以并行化等缺点。

这里本文的核心思想是想要基于GCN+LSTM来实现图网络和时序网络的融合，开发构建更加适合业务需求的时间序列预测模型。

首先是数据集加载，如下所示：

with open("distance.json") as f:
    route_distances = json.load(f)
with open("nodedata.json") as f:
    speeds_array = json.load(f)
route_distances = np.array(route_distances)
speeds_array = np.array(speeds_array)
print(f"route_distances shape={route_distances.shape}")
print(f"speeds_array shape={speeds_array.shape}")

结果输出如下所示：

route_distances shape=(23, 23)
speeds_array shape=(1056, 23)

共包含了23个节点。

之后是创建邻接矩阵，如下：

num_routes = route_distances.shape[0]
route_distances = route_distances / 10000
w2, w_mask = (
    route_distances * route_distances,
    np.ones([num_routes, num_routes]) - np.identity(num_routes),
)
adjacency_matrix = (np.exp(-w2 / sigma2) >= epsilon) * w_mask

结果输出如下所示：

一个简单的GCN+LSTM实现如下所示：

def gcn_layer(adj_matrix, input_features, output_dim):
    # GCN层的实现
    adj_normalized = normalize_adj(adj_matrix) # 对邻接矩阵进行归一化处理
    output = Dense(output_dim)(adj_normalized @ input_features) # GCN的公式实现
    output = Activation('relu')(output)
    return output
 
# 构建GCN+LSTM模型
def build_gcn_lstm_model(adj_matrix, input_dim, hidden_dim, output_dim):
    # 输入层
    inputs = Input(shape=(None, input_dim))
    
    # GCN层
    gcn_output = gcn_layer(adj_matrix, inputs, hidden_dim)
    
    # LSTM层
    lstm_output = LSTM(hidden_dim)(gcn_output)
    
    # 输出层
    outputs = Dense(output_dim, activation='softmax')(lstm_output)
    
    model = Model(inputs=inputs, outputs=outputs)
    model.compile(optimizer=Adam(lr=0.001), loss='categorical_crossentropy', metrics=['accuracy'])
    
    return model

也可以自己定义新的layer都是可以的，如下：

class GCNLSTM(layers.Layer):
 
    def __init__(**kwargs):
        super().__init__(**kwargs)
        self.graph_conv = gcnLayer(in_feat, out_feat, graph_info, **graph_conv_params)
        self.lstm = layers.LSTM(lstm_units, activation="relu")
        self.dense = layers.Dense(output_seq_len)
        self.input_seq_len, self.output_seq_len = input_seq_len, output_seq_len
 
    def get_config(self):
        config = super().get_config().copy()
        return config
 
    def call(self, inputs):
        inputs = tf.transpose(inputs, [2, 0, 1, 3])
        gcn_out = self.graph_conv(inputs) 
        shape = tf.shape(gcn_out)
        gcn_out = tf.reshape(gcn_out, (batch_size * num_nodes, input_seq_len, out_feat))
        lstm_out = self.lstm(gcn_out) 
        dense_output = self.dense(lstm_out) 
        output = tf.reshape(dense_output, (num_nodes, batch_size, self.output_seq_len))
        return tf.transpose(output, [1, 2, 0]) 

之后就可以进行模型的训练了如下：

history=model.fit(X_train,y_train,validation_data=(X_test,y_test),epochs=200)
model.save("model.h5")
plotLoss(history.history["loss"],history.history["val_loss"],"loss.png")

loss可视化如下所示：

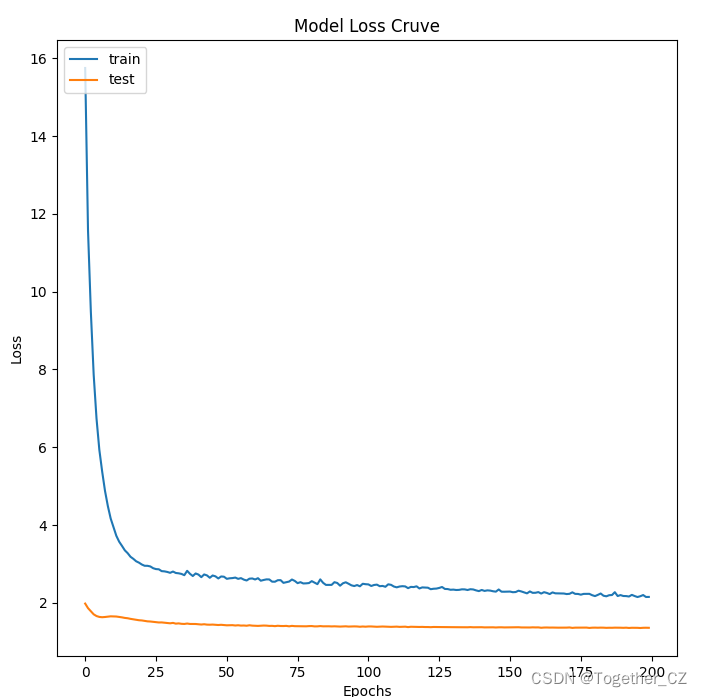
这里我们随机选取了几个node对其数据进行可视化，如下所示：

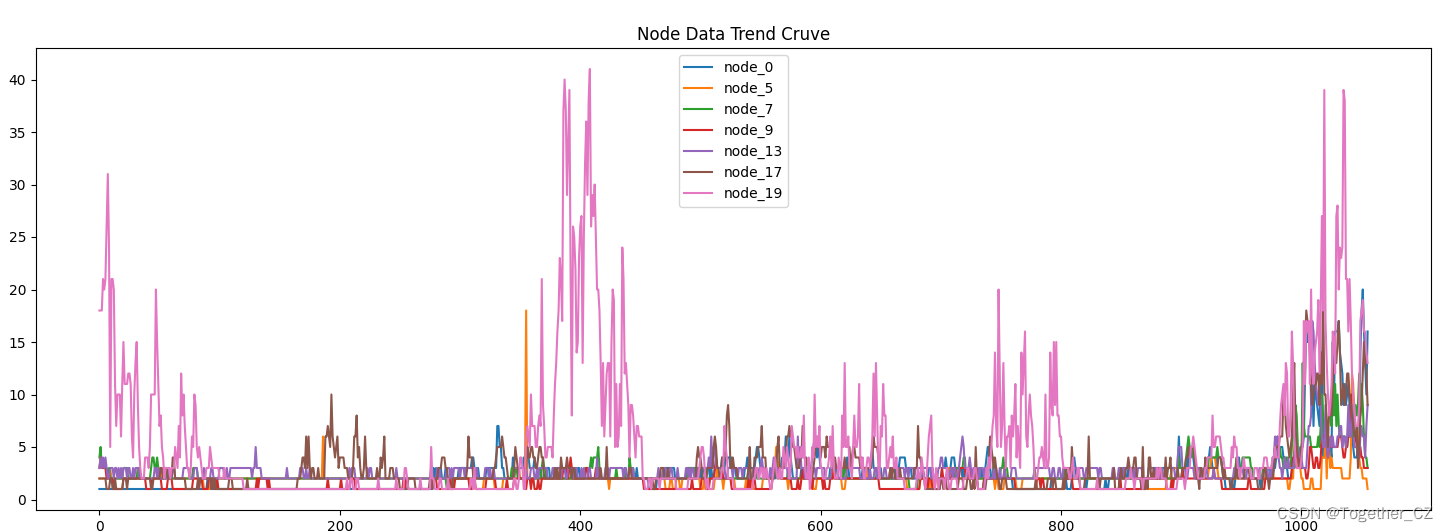
node之间的热力图如下所示：

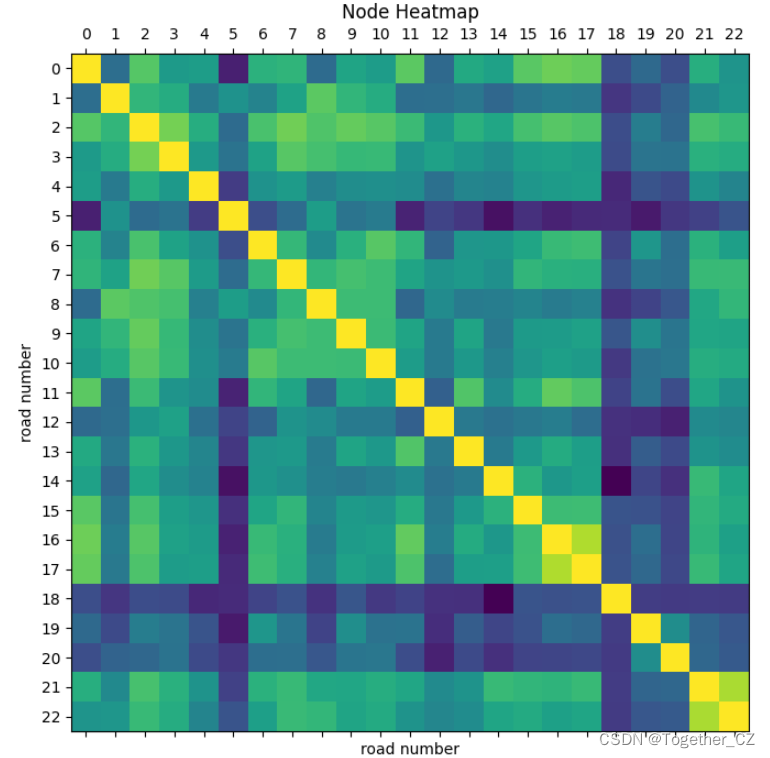
对测试集进行测试评估，对比曲线可视化结果如下所示：

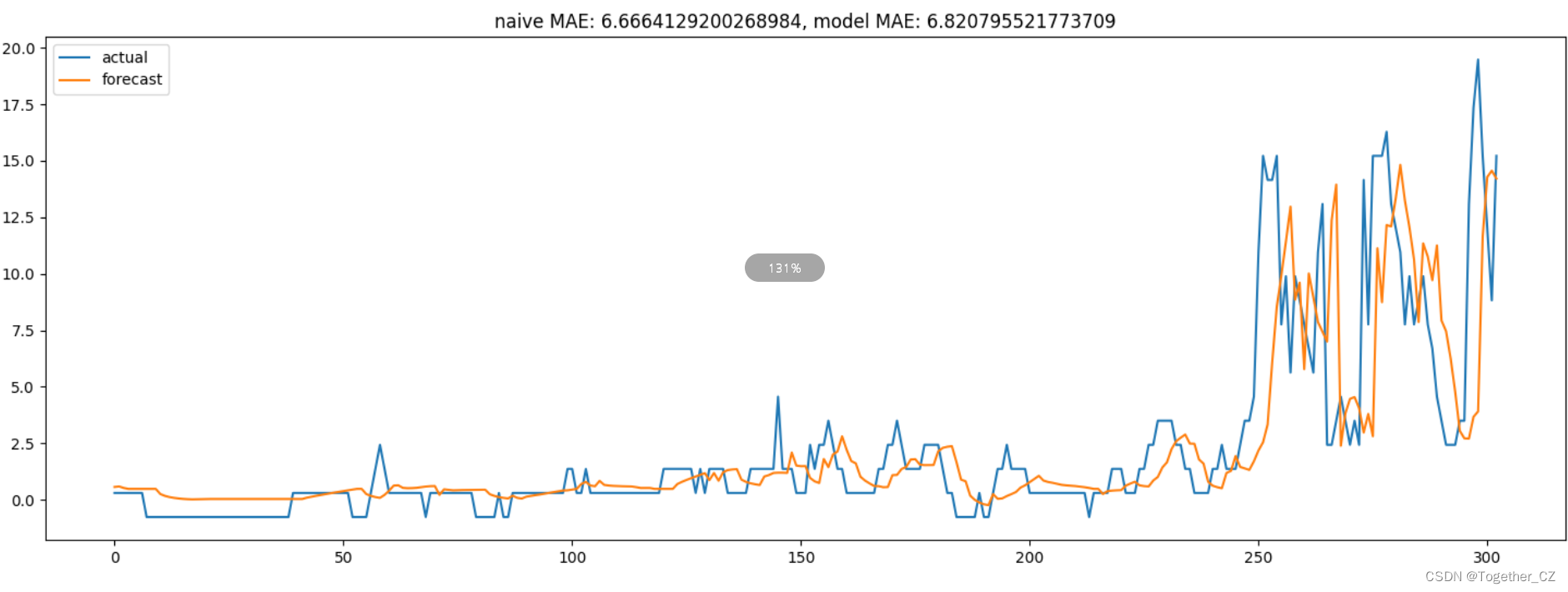
这里对不同node未来时刻进行持续预测，分别展示，如下所示：

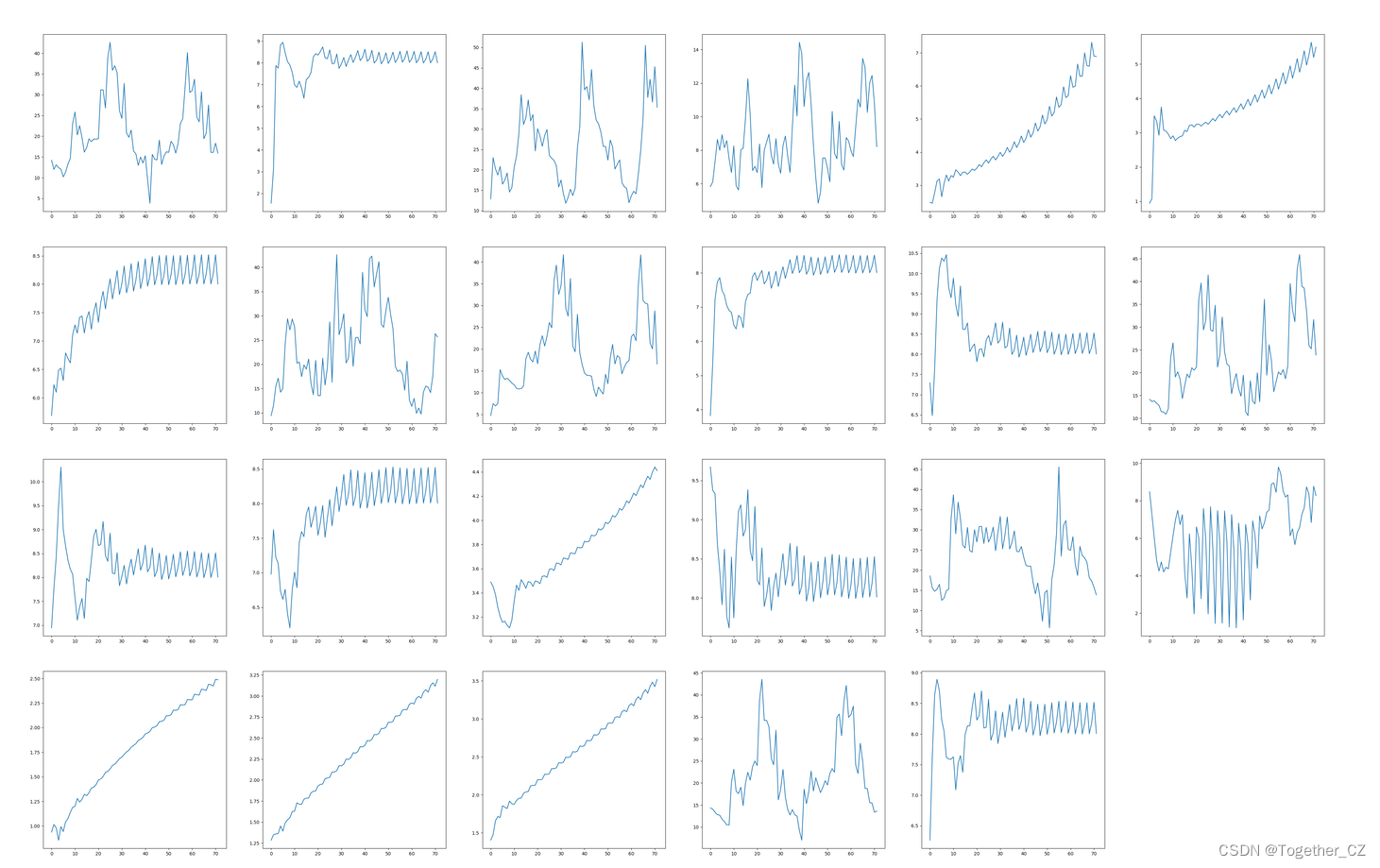
这是一种比较新的建模方式，在实际应用中可以更多捕捉到不同节点的依赖性，这个是比较有用的一点，后续会在实际应用过程中继续挖掘。