【数据结构】实现二叉搜索树的查找、插入和删除功能（思路+图文+代码详解）_删除二叉树的代码数据结构

---

二叉搜索树

---

• HashMap和HashSet的底层是一个哈希表

• TreeMap 和TreeSet底层是一棵搜索树（红黑树）

• 涉及到一些搜索查找的场景可以调用Map和Set接口

一、搜索树

二叉搜素树 又叫 二叉排序树

1.要么是空树

2.如果左子树不为空，则左子树上所有节点的值都小于根节点的值

3.如果右子树不为空，则右子树上所有节点的值都大于根节点的值

4.它的左右子树也是二叉搜索树

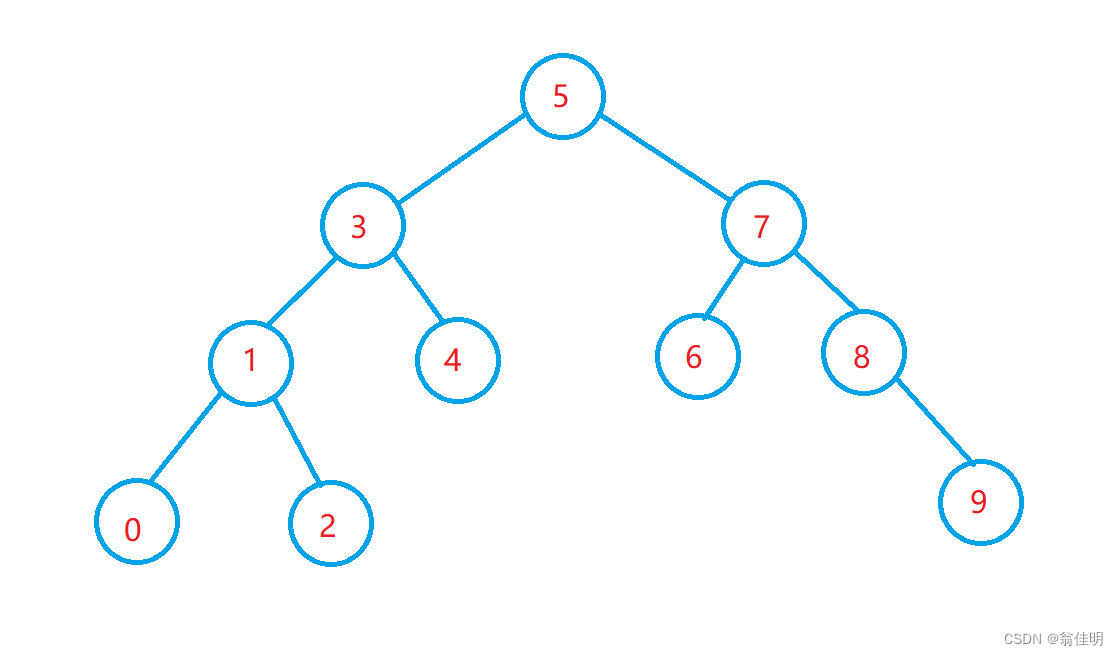
1.二叉搜索树的查找

• 将要查找的值，和根节点比较

• 比根节点小的在左树找，比根节点大的在右树找

最坏情况：按单分支树找， 为树的高度 N

最好情况：完全二叉树、满二叉树，树的高度为log₂N，效率最高

为了解决单分支树的问题，采用AVL树解决。

• AVL树：高度平衡的二叉搜索树，保证高度一直平衡（左右高度差不超过1），需要不断进行旋转，来保持平衡
• 红黑树：加入了颜色，减少了旋转

public class BinarySearchTree {
    static class TreeNode {//静态内部类
        public int val;
        public TreeNode left;
        public TreeNode right;

        public TreeNode(int val) {
            this.val = val;
        }
    }

    public TreeNode root = null;

    /**
     * 查找二叉搜索树中指定的val值
     *
     * @param val
     * @return
     */
    public TreeNode find(int val) {
        TreeNode cur = root;
        while (cur != null) {
            if (cur.val == val) {
                return cur;
            } else if (cur.val < val) {
                cur = cur.left;
            } else {
                cur = cur.right;
            }
        }
        return null;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

• 1.设cur结点为root位置
• 2.cur的val如果小于目标val，cur移动到左子树
• 3.cur 的val如果大于目标val，cur移动到右子树

2.二叉搜索树的插入

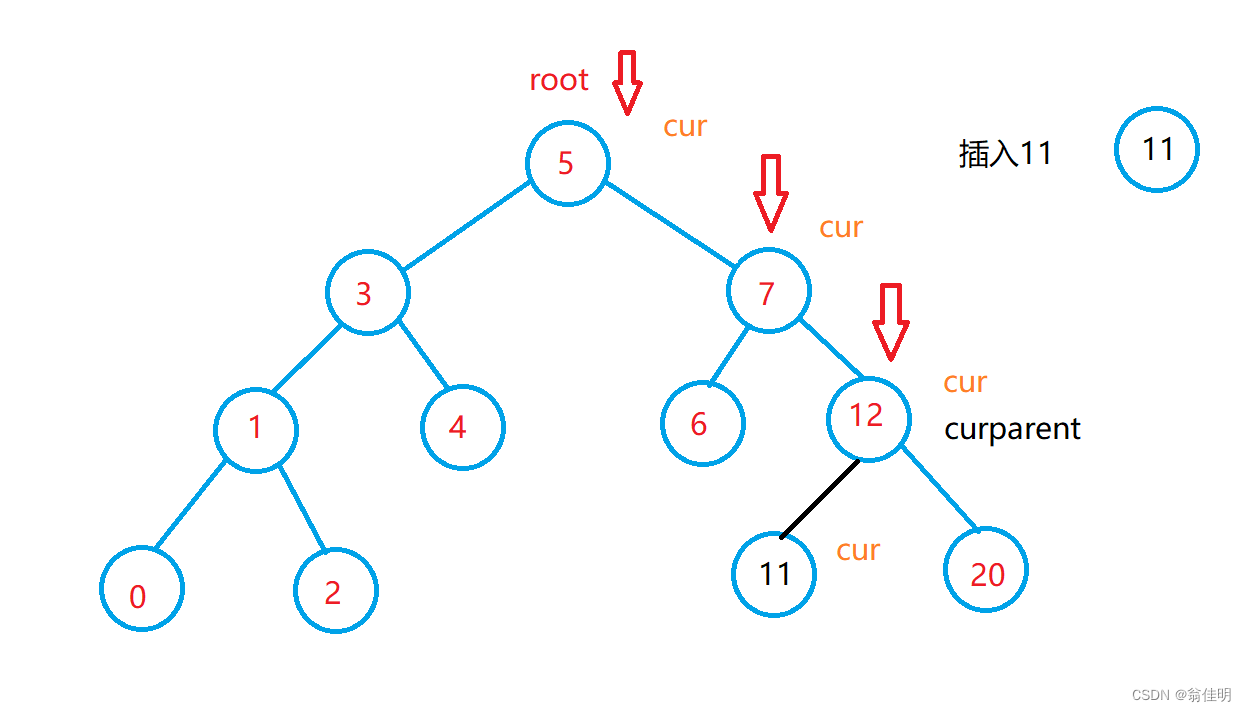
• 1.如果是空树（root==null），直接插入根的位置
• 2.如果不是空树，按照查找的逻辑找到要插入的位置，插入新结点
• 3.都插入到了叶子结点，也就是cur为空时的位置
• 4.所以要记录一个cur的双亲结点，方便cur插入数据

    /**
     * 插入一个数据
     *
     * @param val
     */
    public void insert(int val) {
        //root为空
        if (root == null) {
            root = new TreeNode(val);
            return;
        }
        //root不为空
        TreeNode cur = root;
        TreeNode parent = null;

        //找到cur为空的位置
        while (cur != null) {
            if (cur.val < val) {
                parent = cur;
                cur = cur.right;
            } else if (cur.val > val) {
                parent = cur;
                cur = cur.left;
            } else {
                return;
            }
        }
        //根据判断双亲结点的值来决定插入那个叶子结点
        TreeNode node = new TreeNode(val);
        if (val < parent.val) {
            parent.left = node;
        } else {
            parent.right = node;
        }
    }

    public void inorder(TreeNode root) {
        if (root == null) {
            return;
        }
        inorder(root.left);
        System.out.print(root.val + " ");
        inorder(root.right);
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

3.二叉搜索树的删除

要删除的位置为cur,它的双亲结点为parent

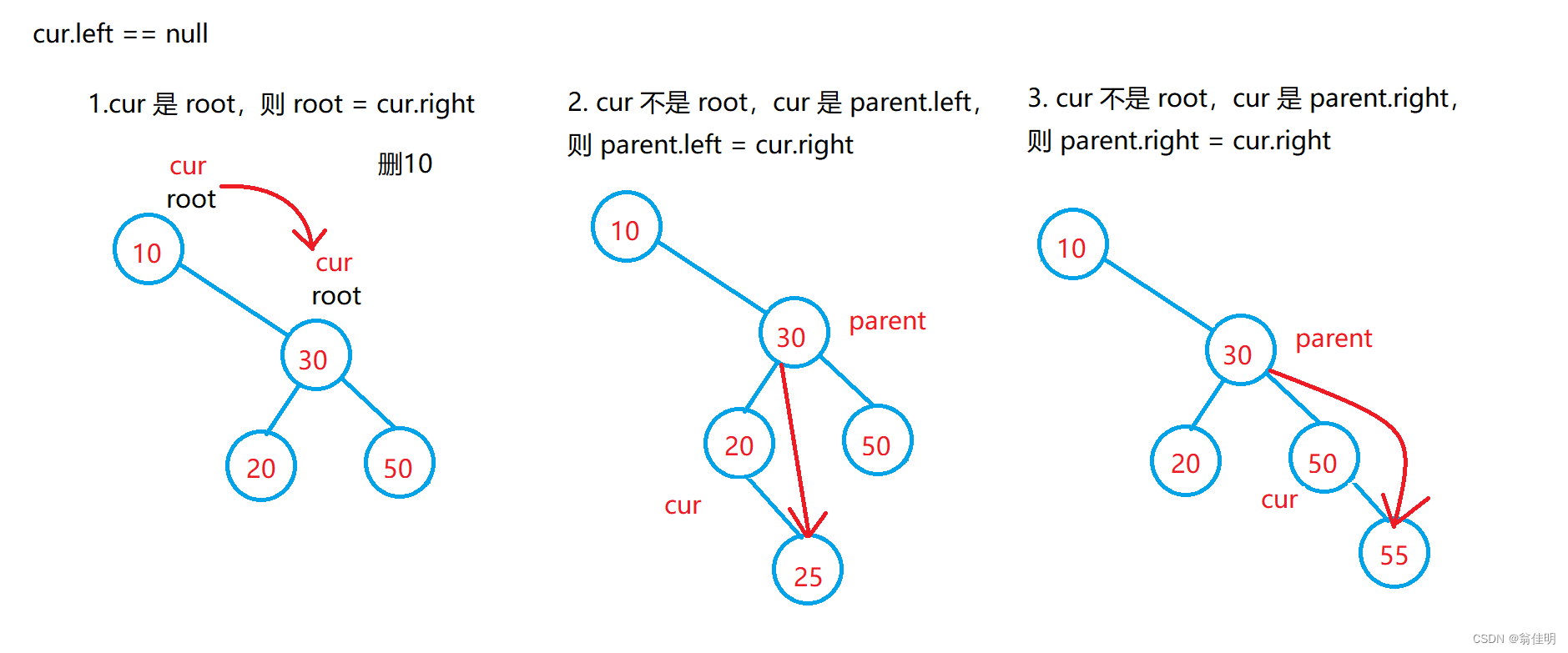
• 1.cur左结点为空：cur.left == null

  1.cur为根节点，cur没有左树，根节点移动到它的右树上

  2.cur不是根节点，此时cur为双亲结点的左结点，cur没有左树，双亲结点的左结点连上cur的右结点 parent.left = cur.right

  3.cur不是根节点，此时cur为双亲结点的右结点，cur没有左树，双亲结点的右结点连上cur的右结点 parent.right = cur.right

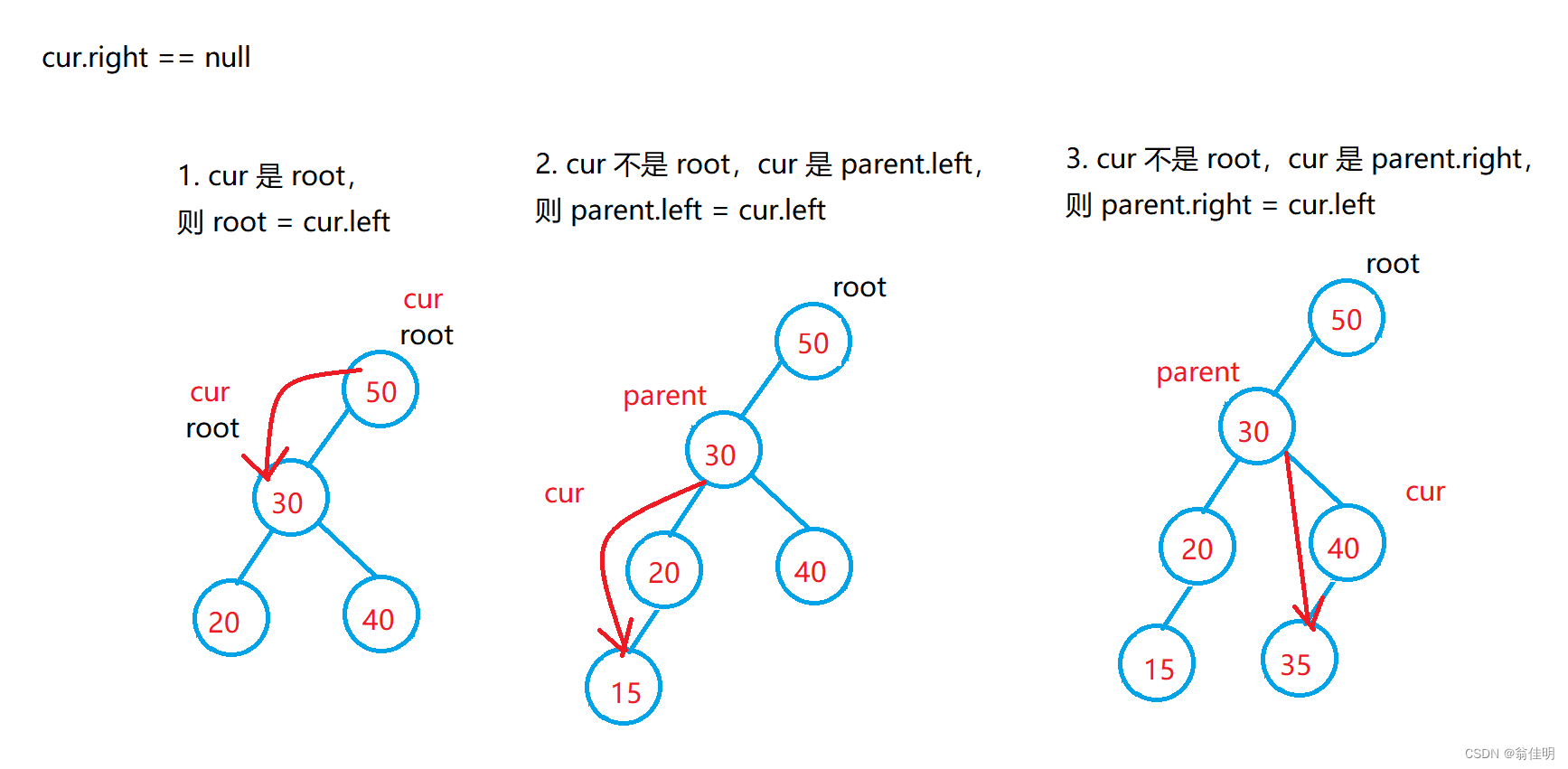
• 2.cur右结点为空：cur.right == null

1.cur为根节点，cur没有右子树，根节点移动到cur的左子树上

2.cur不是根节点，cur是双亲结点的左结点，cur没有右结点，双亲结点的左结点连上cur的左结点

3.cur不是根节点，cur是双亲结点的右结点，cur没有右结点，双亲结点的右结点连上cur的左结点

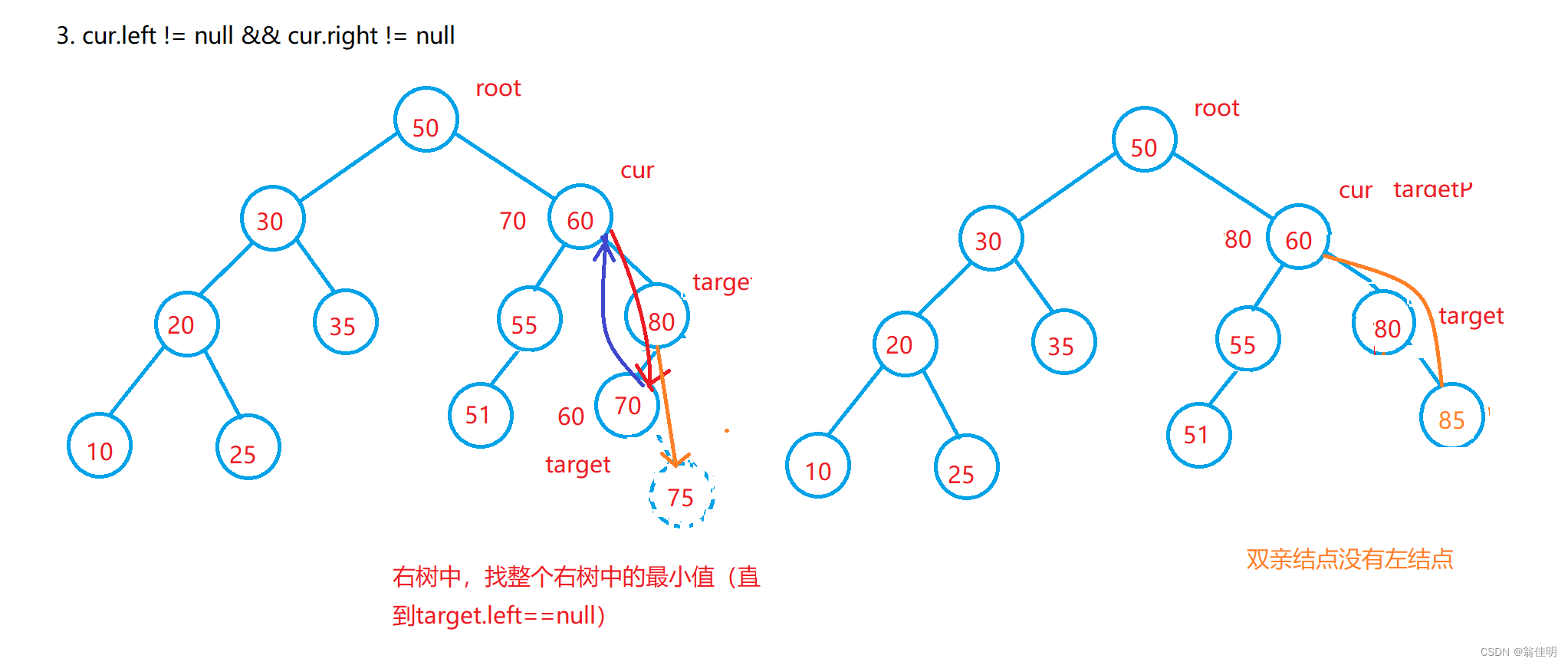
3.左右结点都不为空：cur.left != null && cur.right != null

1.替换法进行删除，在cur的右子树中，找到该子树的最小值，和要删除的值交换

2.最后删除那个替换的结点，维护了二叉搜索树

3.替换的结点在它双亲结点的左边，没有左子树，target.left==nulll，如果有右子树，target双亲结点的左结点连接target的右结点（target的右结点都比target大），没有右子树，连接的是空值

4.替换的结点在它双亲结点的右边(双亲结点没有左结点)，target双亲结点的右结点连接target的右结点

    /**
     * 删除值为val的结点
     *
     * @param val
     * @return
     */
    public void remove(int val) {
        TreeNode cur = root;
        TreeNode parent = null;

        //找到cur结点的位置
        while (cur != null) {
            if (cur.val == val) {
                removeNode(cur, parent);
                return;

            } else if (val < cur.val) {
                parent = cur;
                cur = cur.left;
            } else {
                parent = cur;
                cur = cur.right;
            }
        }
    }

    /**
     * 删除结点的分类情况
     *
     * @param cur
     * @param parent
     */
    private void removeNode(TreeNode cur, TreeNode parent) {
        if (cur.left == null) {
            //cur的左结点为空
            if (cur == root) {
                root = cur.right;
            } else if (cur == parent.left) {
                parent.left = cur.right;
            } else {
                parent.right = cur.right;
            }

        } else if (cur.right == null) {
            //cur的右结点为空
            if (cur == root) {
                root = cur.left;
            } else if (cur == parent.left) {
                parent.left = cur.left;
            } else {
                parent.right = cur.left;
            }
        } else {
            //cur的左右结点都不为空
            TreeNode target = cur.right;//在右树中找最小值
            TreeNode targetParent = cur;
            while (target.left != null) {
                targetParent = target;
                target = target.left;
            }//找最小值
            cur.val = target.val;//替换
            if (target == targetParent.left) {
                targetParent.left = target.right;
                //目标值在双亲结点的左边
            } else {
                targetParent.right = target.right;
                //目标值在双亲结点的右边
            }
        }
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72

4.性能分析

插入和删除操作都必须先查找，查找效率代表了二叉搜索树中各个操作的性能

• 即结点越深，则比较次数越多
• 插入的次序不同，可能得到不同结构的二叉搜索树

最好情况：二叉搜索树为完全二叉树，平均计较次数：log₂N

最坏情况：二叉树退化成单分支树，平均比较次数为 N/2

点击移步博客主页，欢迎光临~