- 1银河麒麟linux系统如何禁用触摸板_麒麟系统 设置触摸板在有鼠标的情况下禁用
- 2CSerialPort教程(1) - CSerialPort项目简介
- 3FRP内网穿透 + Nginx代理 + 获取真实IP_nginx grpc ip穿透
- 4Docker Resources
- 5通过命令iostat,iotop查看Linux系统IO性能,信息指标分析详解_d_await指什么
- 6Visual Studio安装MFC开发组件
- 7GoWeb——Gin框架的使用_fabric-sdk-go与gin框架应用
- 8Web3小白解惑系列:区块链入门(第三弹)_比特币halving
- 9使用c++类模板和迭代器进行List模拟实现
- 10C++领域新星创作者的申请与创作流程分享_csdn创作者认证要上传什么资料
模块优化加速_惯性导航系统中浮点计算加速单元设计
赞
踩
随着微机电系统(MEMS)技术的发展,石英振梁加速度计作为一种新型MEMS惯性传感器的全数字脉冲输出,越来越广泛应用于小型飞机、机器人导航系统等[1-2]。为了使该器件能在惯导系统中发挥出其优良性能,需要对其输出频率脉冲信号高精度测量的计数值进行浮点计算。
然而随着超大规模集成电路设计技术的发展,在中,大多数DSP处理器具有双精度浮点运算能力,但在这其中存在大量的运算,会耗用CPU大量的计算能力,并且采用功能级流水增加了面积开销和硬件复杂度[3]。通过软件设计实现,不仅占用大量的软件资源,而且运行速度慢,这些设计方法不太适合一些高速数据采集和处理应用场合[4]。
根据石英振梁加速度计的特性,在惯性导航系统中,为了优化频率转换的计算速度,本文提出一种面向频率转换应用的浮点计算加速单元设计,对加速度计测量的计数值进行浮点计算,以加快运算的换算速度,减轻了导航计算机中处理器的负担,从而加快导航姿态解算的速度。采用FPGA对浮点计算加速单元进行了实验验证,与传统的软件计算方法进行了比较,加速度解算速度提高了2倍,可以很好地提升惯性导航系统的性能。
1 总体设计
1.1 石英振梁加速度计原理
石英振梁加速度计是一种基于石英振动梁的力-频特性的新型高精度固态传感器。其内部交变电场使其推挽方式安装的两个石英梁在伸缩振动模式下进行振动。当加速度计受到外部加速时,敏感质量块产生一个惯性力以分别作用于这两个石英梁上。其中一个石英梁受到压缩作用,其谐振频率会降低;而另一个受到拉伸作用,其谐振频率将升高。最终这两个石英梁的频率差与外施加力成比例,即与加速度成比例,进而测量出加速度值[5]。
因此每个加速度计将输出两个频率信号,这两个频率信号之差与加速度的关系如下:
其中L0≤0.9 g,为零偏值;L1为标度因数,典型值为50 Hz/g;L2为二阶非线性系数,L2≤20 μg/g2;f1为力敏感石英梁F1的输出,单位为Hz;f2为力敏感石英梁F2的输出,单位为Hz;a为即时加速度计,单位为g。
1.2 系统架构设计
传统的惯性导航系统架构设计如图1所示,首先系统对三个石英振梁加速度计和三个陀螺仪进行数据采集。三个石英振梁加速度计的输出信号和温度信号均为频率信号,每个加速度计输出2路频率信号。根据式(1)可知,要得到加速度,就要测出2个石英梁的频率输出值,则设计的频率采样系统就必须能对9路通道的频率信号进行高精度测量与快速计算。系统对加速度计进行高精度测频,使用的是等精度测频法,其公式为:
其中fs为标准频率,Ns为标准频率信号脉冲个数,fx为被测频率,Nx为被测频率信号脉冲个数。
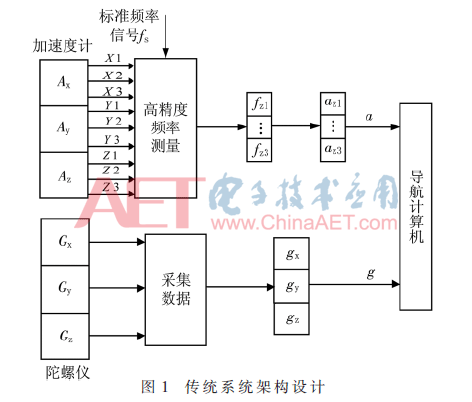
根据式(2),经过频率转换计算得到测频值,然后由式(1)可知,频率值转换后进而得出加速度值。同时三个陀螺仪经过脉冲测量后得到角速度,最后将得到的加速度值和陀螺仪测得的角速度值输入到导航计算机进行后续的解算。
系统设计实现流程图如图2所示,加速度计测量的频率值经过转换得到加速度,再通过姿态解算可得到姿态角θα,角速度通过积分算出角度θg,使用互补滤波算法进行数据融合,可得到最终的姿态角θ。
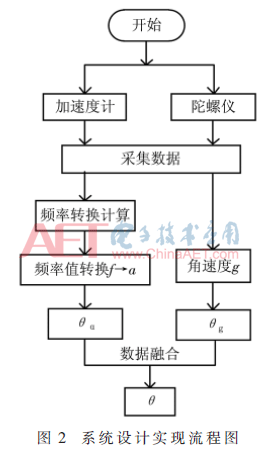
而在传统的系统架构设计中,频率转换计算会耗用大量的时间,为了加快频率转换的计算速度,本文设计了一种面向频率转换应用的浮点计算加速单元。如图3所示,在加速度计高精度频率测量模块后设计了FPU模块,此模块主要是在FPGA芯片里面完成的。设计时,选用了Xilinx公司的XC3S1400AN芯片。在下一节将对浮点计算加速单元的实现进行详细介绍。
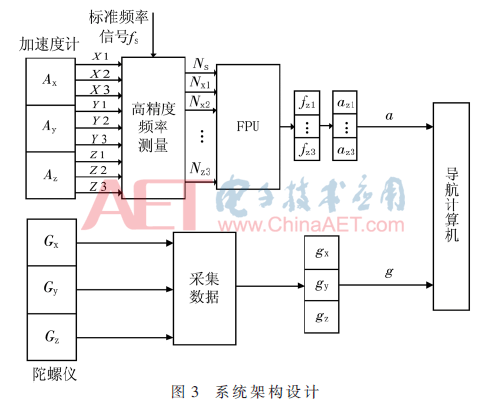
2 加速单元的实现
浮点计算是以9路频率计数值的顺序执行,即按照X1、X2、X3、Y1、Y2、Y3、Z1、Z2和Z3的顺序执行,在相应的计数器值锁定完成后立即开始浮点计算。浮点计算过程如图4所示,主要包括:乘法模块、定点浮点转换(规格化)、浮点除法、结果锁存4个过程,最终计算结果为满足IEEE-754标准[6]的规格化双精度浮点数。
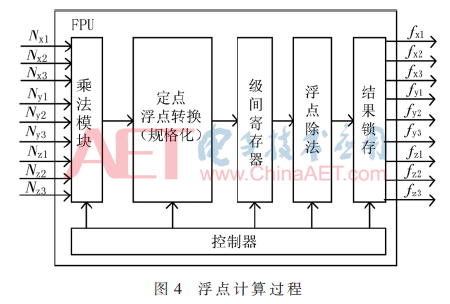
2.1 浮点计算的实现
2.1.1 乘法模块
一个浮点计算过程首先是9路通道的计数值并行输入到乘法模块,然后按照X1,X2,X3,Y1,Y2,Y3,Z1,Z2和Z3的顺序将fs与Nx,y,z进行乘法计算。其过程在对应的计数值锁存完成后,立即开始浮点计算。9路通道根据控制器来选择其中一个通道的计数值进入乘法模块做乘法计算。本文是根据工程所需,选用标准频率fs为80 MHz,通过分步相加实现的乘法计算。
2.1.2 规格化
在控制器的控制下,对fs与Nx,y,z相乘得到的结果进行规格化处理,即先判断计算的尾数结果是否符合规格化的格式,如果不符合,则将其进行移位处理,并对指数做相应的加减操作。9路通道的计数值计算完成后都要进行规格化处理。
2.1.3 级间寄存器
对fs与Nx,y,z相乘得出的结果进行计算前导0数量,即找出最高1的位置。在控制器的控制下,锁存到寄存器1和寄存器2中;使用最高1位置值加上指数偏移值,就是规格化后的指数。再根据最高1的位置,把其后的有效数字锁存到浮点尾数从最高位开始的位置,尾数低位补0。对于扩展标志,只有0与非0两种情况,如果计数值为全0,扩展标志为00,否则为01(表示正常数)。
2.1.4 浮点除法
在控制器的控制下,将对级间寄存器中的数据进行浮点除法运算。根据浮点除法运算必需的步骤,设计浮点除法整体单元如图5所示[7]。本设计由6个部分构成,即预处理、尾数除、指数减、异常处理、规格化与舍入、溢出判断与输出,其中尾数除是通过SRT基4算法[8]来实现的。
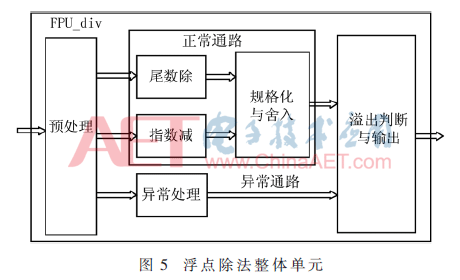
浮点计算是在乘法计算模块到浮点除法模块的过程中使用了流水线结构,当第一通道完成乘法计算后,立即送到下一模块进行相应的数据处理,进而将其送到浮点除法模块做最终计算。同时第二通道在处理其他数据,以此顺序执行运算。
本文在浮点除法过程中采用非流水线结构,此结构是以串行形式的迭代运算实现的,在每次迭代时都共用同样的硬件,产生的部分余数和部分商均在寄存器中更新。此过程是在9路全部完成最终计算后,再继续下一数据处理。
2.1.5 结果锁存
在控制器的控制下,对浮点除法模块计算的最终结果进行锁存,然后浮点输出。在以石英振梁加速度计为基础的惯性导航系统中,此结果经过转换为加速度后进行姿态解算。
2.2 控制器的实现
本文利用硬件描述语言VHDL实现对浮点加速单元进行逻辑设计。在整个控制过程中,乘法模块是由乘法变成加法计算的,使用7个加法器就可以实现乘法计算,3个周期即可计算出结果。
在乘法计算模块到浮点除法模块的过程中使用了两级流水线结构。图6所示为乘法计算模块到浮点除法模块的工作图,首先是在控制器的控制选择通道下,第一个通道输入计数器数据有效后进行乘法计算,等待乘法计算完成后,对其计算的结果进行规格化处理也就是定点浮点转换。两个周期后,待规格化数据输出稳定后,将其计算的结果锁存到M1。一旦锁存完成后,立即启动浮点除法计算单元,进行浮点除法运算。等待浮点除法完成后,在控制器的控制下,选择相应通道的地址将其计算的结果锁存到D1,同时系统在控制器的控制下,选择第二个通道数据输入到乘法计算模块做乘法计算,并将规格化后的计算结果锁存到M2,这时也将第三个通道的计数值输入到乘法计算模块。整个浮点计算过程以这种工作方式来完成9路通道数据的全部计算。
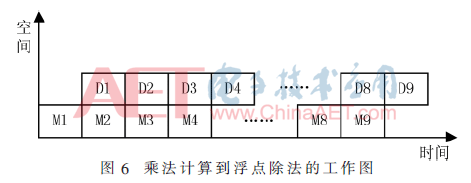
浮点除法模块是用非流水线结构来实现的,每次浮点除法计算需要26个周期,因此,采用图4所示的部件级流水结构,完成9个频率值的浮点计算共需要260个周期。
如果用流水线结构实现浮点除法运算[8],则只需要35个周期就可以完成9次浮点除法运算,但会耗用大量的面积资源。
本文对这两种实现方式都进行了实现与验证,经过综合分析后得出,虽然全流水线结构处理数据速度快,但面积开销大。而部件级流水线结构,除法计算采用非流水结构,速度虽然慢,但也能满足要求,面积开销以及性能均得到了优化折中。
3 结果与验证
3.1 实验验证
本文在惯性导航系统中,对浮点计算加速单元进行程序编写、综合及外部端口的输出状态的波形观测与验证,并在XC3S1400AN芯片上对其进行了硬件测试。
通过验证结果表明,设计的浮点计算输出为64位的双精度浮点数,结果正确,并且完全符合要求。另外,采用全流水线结构和部件流水结构设计的浮点计算加速单元经过综合、布局布线后,占用资源情况如表1所示。通过两种方法对比可以看出,全流水线结构实现浮点计算,其面积开销为24%,而部件流水结构的浮点计算加速单元只需4%的面积开销,也就是说全流水结构实现的浮点计算所消耗的面积资源是部件流水设计的6倍。与全流水线结构实现浮点计算相比,明显可以看出本文设计的部件流水结构的浮点计算加速单元极大地减少了面积开销。
3.2 性能验证
本文对性能进行了测试,系统使用的处理器为TMS320C6713(工作频率为100 MHz)。首先系统对三个加速度计和三个陀螺仪进行数据采集,之后对加速度计做频率转换计算,再将频率值转换成加速度值,经过姿态解算得到姿态角。同时三个陀螺仪再做软件计算,经过脉冲测量后得到角速度,角速度通过积分得到角度。然后使用互补滤波算法进行角度融合,整个过程运行时间为95.8 μs。而采用本文设计的全流水线结构、部件流水结构的浮点计算加速单元实现频率转换计算,整个解算过程运行时间均为27.8 μs。与软件计算方法相比,运行时间减少了70.9%,速度提高了2倍。
4 结论
本文设计了一种面向频率转换应用的浮点计算加速单元,在实际的导航计算机系统中进行了实现验证,功能正确可靠。使用本文设计的浮点计算加速单元,从数据采样到频率转换,再经过频率值转换成加速度进行姿态解算;陀螺仪测得的角速度再进行积分,最后进行数据融合,速度提高了2倍。相比使用全流水线结构,本文设计的部件流水结构的浮点计算加速单元的FPGA面积开销仅为其1/5。
参考文献
[1] ZHI W,CHU J,LI J,et al.A novel attitude determination system aided by polarization sensor[J].Sensors,2018(18):158.
[2] 杨挺,杨贵玉,李庆丰.石英振梁加速度计静态输入输出特性[J].中国惯性技术学报,2014,22(3):386-390.
[3] 苑佳红.Stratus HLS工具在高性能双精度浮点乘法设计中的应用流程[J].电子技术应用,2018,44(8):20-30.
[4] 朱峰,鲁征浩,朱青.形式化验证在处理器浮点运算单元中的应用[J].电子技术应用,2017,43(2):29-32.
[5] 冯丽爽,王文璞,周震,等.石英振梁加速度计谐振器的结构设计[J].中国惯性技术学报,2013,21(1):101-105.
[6] ZURAS D,COWLISHAW M,AIKEN A,et al.IEEE standard for floating-point arithmetic[S].IEEE Std 754-2008,2008:1-70.
[7] 陈勋.基于SRT4算法的浮点除法/方根算术单元设计[D].西安:西安电子科技大学,2016.
[8] A VHDL library of parametrisable floating-point and LNS operators for FPGA[DB/OL].(2006-07-31)[2019-01-22].http://www.ens-lyon.fr/LIP/Arenaire/Ware/FPLibrary.
作者信息:
田换换1,2,朱晓燕1
(1.首都师范大学 信息工程学院,北京100048;2.电子系统可靠性技术北京市重点实验室,北京100048)


