数据结构与算法之中序遍历

中序遍历是一种二叉树的遍历方式，其遍历顺序为先遍历左子树，然后遍历根节点，最后遍历右子树。具体的过程如下：

1. 如果当前节点的左子树非空，则递归遍历左子树。

2. 访问当前节点。

3. 如果当前节点的右子树非空，则递归遍历右子树。

中序遍历是二叉搜索树中最常用的遍历方式之一，因为它可以将树中所有节点按照大小顺序输出。在实际应用中，中序遍历常用于查找二叉搜索树中的某个节点，或者对二叉搜索树中的节点进行排序。

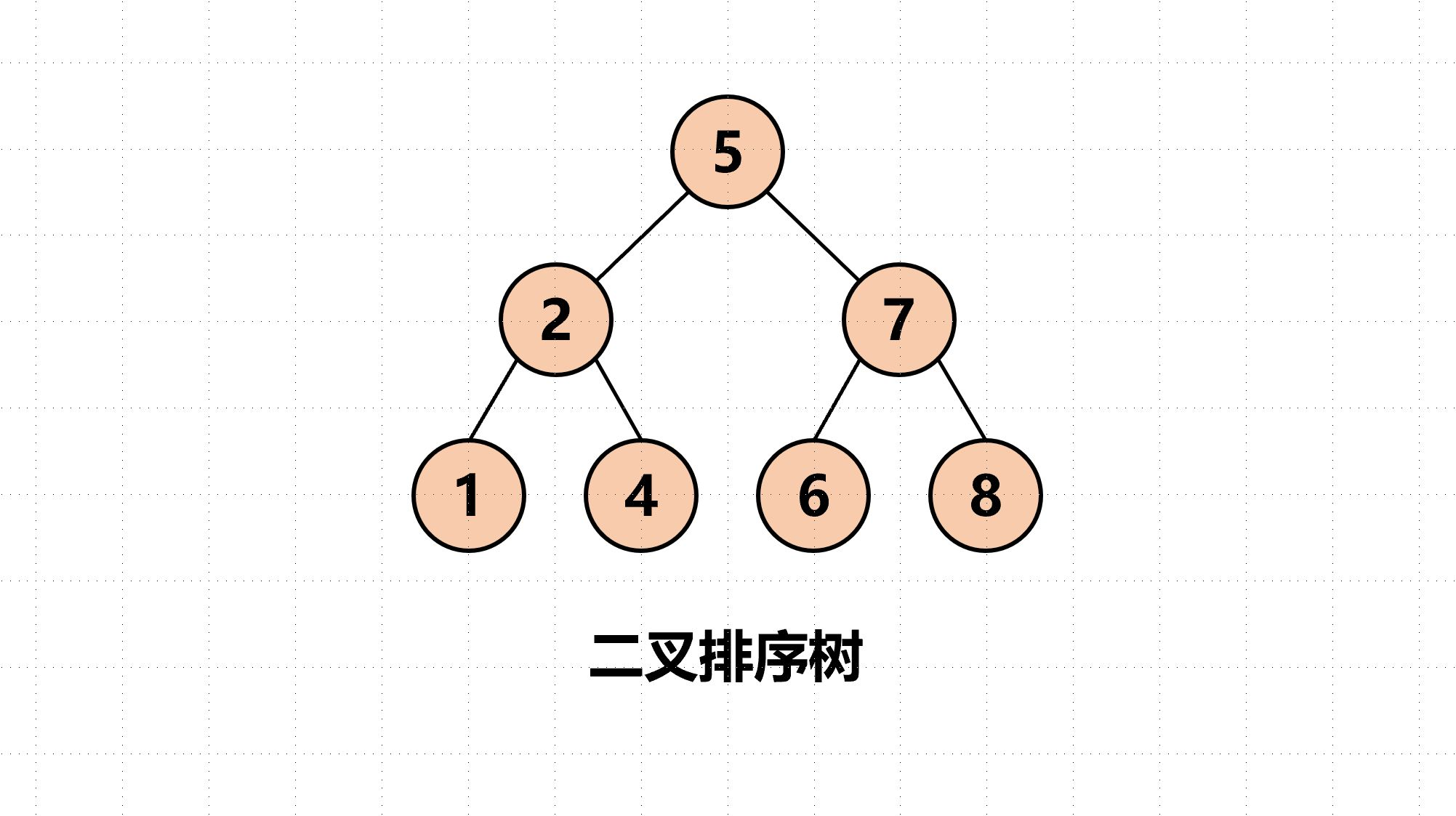
一、C 实现 中序遍历 及代码详解

中序遍历是二叉树的一种遍历方式，指先遍历左子树、再遍历根节点、最后遍历右子树的顺序。中序遍历在二叉搜索树中尤为常用，可以按照元素从小到大的顺序输出。

以下是中序遍历的 C 语言实现：

#include <stdio.h>
#include <stdlib.h>

// 定义二叉树结构体
struct node {
    int data;
    struct node *left;
    struct node *right;
};

// 中序遍历函数
void inorder(struct node *root) {
    if (root != NULL) {
        inorder(root->left);
        printf("%d ", root->data);
        inorder(root->right);
    }
}

// 创建新节点函数
struct node *newNode(int data) {
    struct node *node = (struct node*)malloc(sizeof(struct node));
    node->data = data;
    node->left = NULL;
    node->right = NULL;
    return node;
}

int main() {
    struct node *root = newNode(1);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->left = newNode(4);
    root->left->right = newNode(5);

    printf("中序遍历结果：\n");
    inorder(root);

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

上述代码中，我们首先定义了一个二叉树的结构体 node，包括数据域 data、左子树指针 left 和右子树指针 right。接着，我们编写了一个中序遍历的函数 inorder，用递归的方式实现了中序遍历的顺序，先递归左子树再输出根节点，最后递归右子树。最后，我们编写了一个创建新节点的函数 newNode，用于为二叉树插入新的节点。

在 main 函数中，我们创建了一棵二叉树，并调用了 inorder 函数进行中序遍历。程序输出的结果即为中序遍历的顺序。

该代码实现了二叉树的中序遍历，并通过例子展示了如何创建和遍历一棵二叉树。

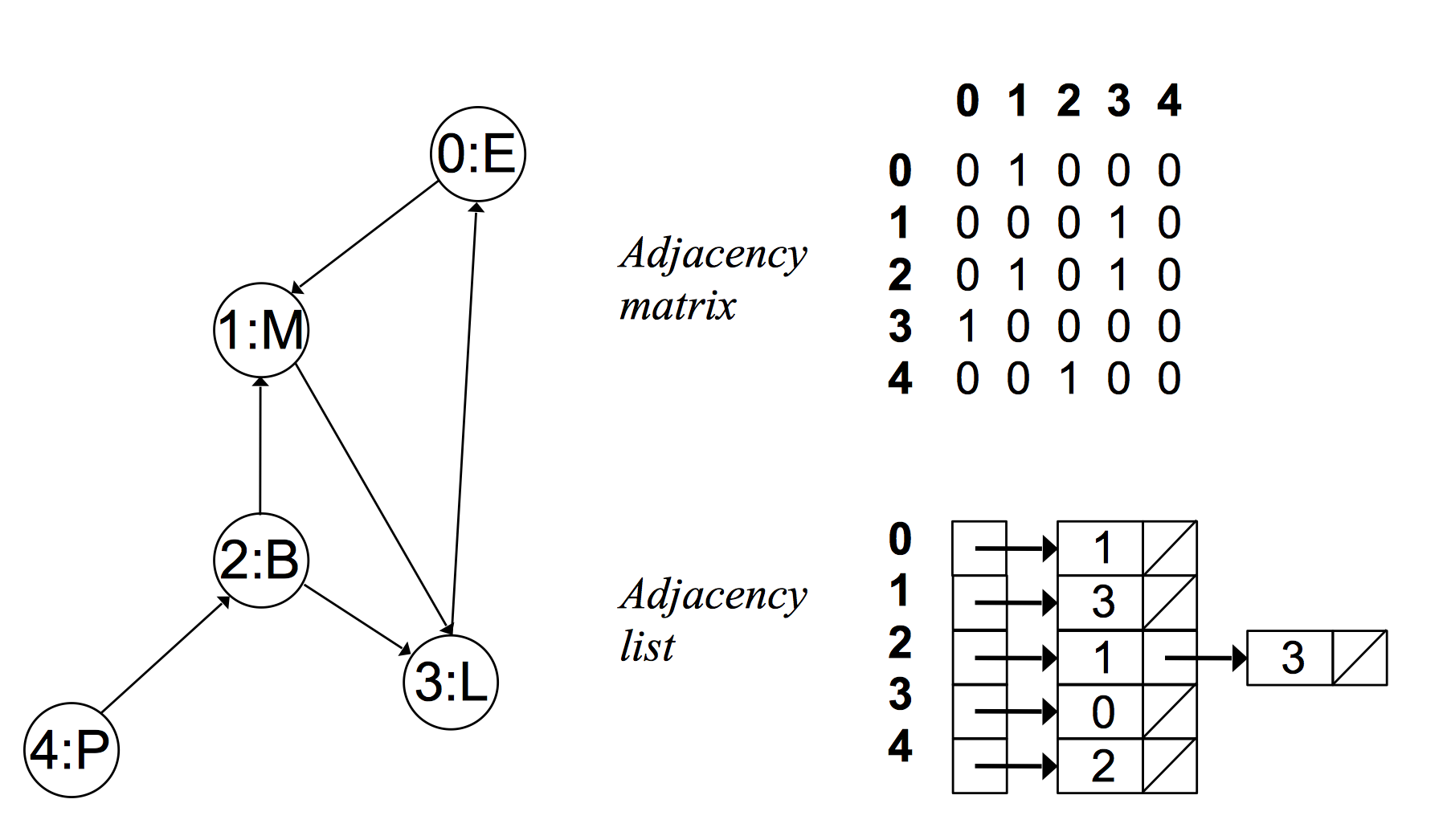
二、C++ 实现 中序遍历 及代码详解

中序遍历是二叉树遍历的一种方式，它按照节点的左孩子、节点本身、右孩子的顺序遍历。具体实现过程如下：

1. 如果当前节点为空，返回。
2. 对当前节点的左子树进行中序遍历。
3. 访问当前节点。
4. 对当前节点的右子树进行中序遍历。

下面是中序遍历的 C++ 代码实现：

#include <iostream>
using namespace std;

//定义二叉树节点结构体
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

class Solution {
public:
    void inorderTraversal(TreeNode* root) {
        if (root == NULL) return;
        inorderTraversal(root->left);
        cout << root->val << " ";
        inorderTraversal(root->right);
    }
};

int main() {
    //创建二叉树
    TreeNode *root = new TreeNode(1);
    root->left = new TreeNode(2);
    root->right = new TreeNode(3);
    root->left->left = new TreeNode(4);
    root->left->right = new TreeNode(5);

    Solution s;
    cout << "中序遍历结果为：";
    s.inorderTraversal(root);
    cout << endl;

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

代码解释：

1. 定义了一个 TreeNode 结构体，表示二叉树节点。其中，val 表示节点的值，left 和 right 分别表示节点的左孩子和右孩子。
2. inorderTraversal 是中序遍历函数，如果当前节点为空，返回；否则，先递归遍历左子树，再访问当前节点的值，最后递归遍历右子树。
3. 在主函数中，创建了一个二叉树，使用 inorderTraversal 函数进行中序遍历，并将结果输出到屏幕上。

这样，就完成了二叉树中序遍历的实现。

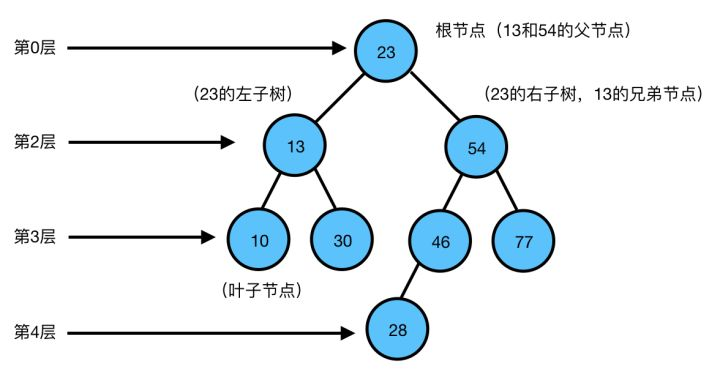
三、Java 实现 中序遍历 及代码详解

中序遍历是二叉树遍历的一种方式，它的遍历顺序是：先遍历左子树，然后访问根节点，最后遍历右子树。在 Java 中，可以通过递归实现中序遍历。

以下是 Java 中序遍历的代码实现及详解：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if (root == null) {
            return res;
        }
        inorderTraversal(root, res);
        return res;
    }

    private void inorderTraversal(TreeNode root, List<Integer> res) {
        if (root == null) {
            return;
        }
        inorderTraversal(root.left, res);
        res.add(root.val);
        inorderTraversal(root.right, res);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

代码实现的逻辑如下：

1. 首先，定义一个方法 inorderTraversal，返回类型为 List<Integer>，参数为根节点 root。

2. 在 inorderTraversal 方法中，定义一个空的 List<Integer> 类型的变量 res，用于存储遍历结果。

3. 如果根节点 root 为 null，直接返回空的结果列表 res。

4. 调用 inorderTraversal 方法的重载方法 inorderTraversal(TreeNode root, List<Integer> res)，进行递归中序遍历。

5. 重载方法 inorderTraversal(TreeNode root, List<Integer> res) 的实现如下：

   a. 如果根节点 root 为 null，直接返回。

   b. 先遍历左子树，调用 inorderTraversal 方法递归访问左子树。

   c. 访问根节点 root，将当前节点的值添加到结果列表 res 中。

   d. 最后遍历右子树，调用 inorderTraversal 方法递归访问右子树。

6. 中序遍历完成后，返回结果列表 res。

该算法的时间复杂度为 O(n)，其中 n 是二叉树的节点数，因为需要遍历每一个节点。空间复杂度为 O(n)，因为需要存储每一个节点的值。