分治算法及常见示例

1、原理

分为三个阶段：

-Divide:整个问题划分成多个子问题

-Conquer:求解各子问题的解

-Merge:合并子问题的解，形成原始问题的解

2、示例

(1)整数乘法

输入：n位二进制整数X,Y

输出：X、Y的乘积

通常计算X*Y时间复杂性是O(n²),现给出一个时间复杂性为O(n^1.59)的算法。

将X,Y表示成X=A2^n/2+B,Y=C2^n/2+D

则X*Y=(A2n/2+B)*(C2n/2+D)=AC2n+(AD+BC)2^n/2+BD

而AD+BC=(A-B)(C-D)+AC+BD。

计算步骤：

• 划分产生A,B,C,D
• 计算A-B,C-D
• 计算n/2位乘法AC,BD,(A-B)(C-D)
• 计算AC+BD+(A-B)(C-D)
• 计算XY

则T(n)=3T(n/2)+O(n)使用master定理得到T(n)=n^1.59.

(2)矩阵乘法

输入：两个n*n矩阵AB

输出：A*B

• 通常计算矩阵乘积时间复杂度是O(n³)，这里给出一个O(n^2.81)的算法。
• 将A、B分为四个子矩阵
  .
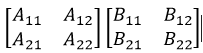• 计算n/2*n/2的矩阵的10个加减和7个乘法

          

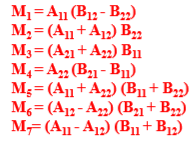
• 则
  

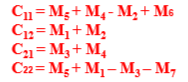
所以T(n)=7T(n/2)+O(n²),根据master定理可得T(n)=O(n^2.81).

(3)找最近点对

输入：n个点的集合Q(两维)

输出：

Preprocessing:

• 若Q中仅包含一个点，则算法结束；
• 把Q中点分别按照x y坐标值排序

Divide:

• 计算Q中各点的x坐标值的中位数m;
• 用x=m将Q划分成两个点集为Q_L,Q_R.

Conquer:

• 递归地在Q_L,Q_R中找到最近点对
  
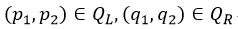
• 令
  

Merge:

• 在临界区查找距离小于d的点对
  
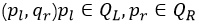
• 若找到，则(p_l,q_r)是Q中最接近点对，否则(p₁,p₂)和(q₁,q₂)中距离最小者为Q中最接近点对

(p_l,q_r)的搜索方法：

 

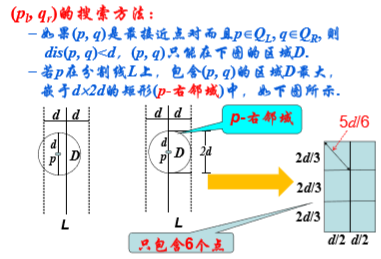
时间复杂度：

T(n)=2T(n/2)+O(n),则T(n)=O(nlogn)

(4)找到convex hull

输入：平面上的n个点的集合Q

输出：CH(Q)：Q的凸包。

【注：Q的凸包是一个多边形P，Q的点或者在P上或者在P内，连接P内任意两点的边都在P内】

Graham-scan算法：

 

 

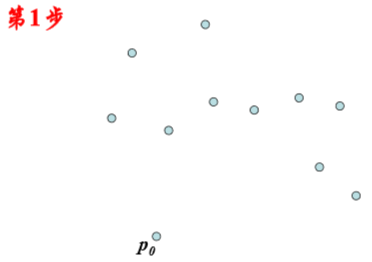
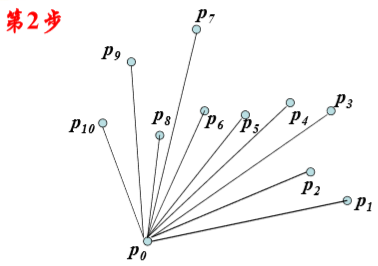
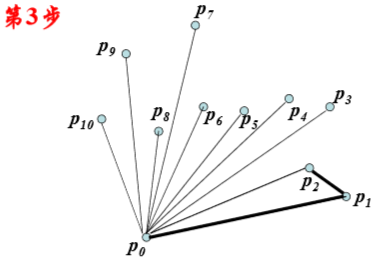
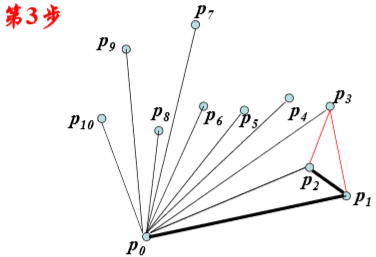
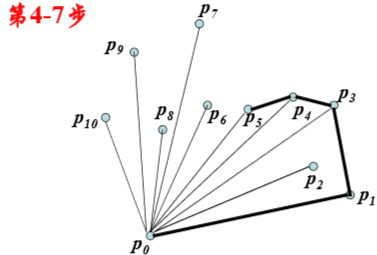
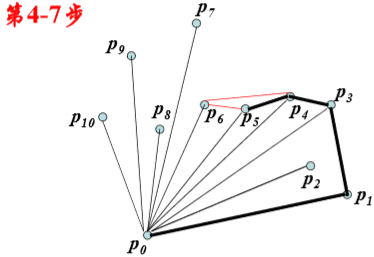
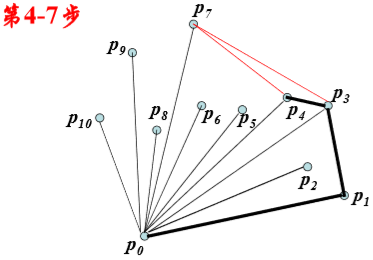
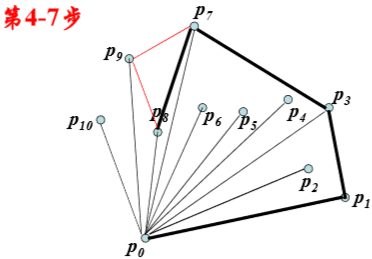
时间复杂性分析：

T(n)=2T(n/2)+O(n),则T(n)=O(nlogn)

--------------------------------------^_^我是可爱的分割线^_^--------------------------------------------------

1、友谊点对

2、黑白点匹配

3、求反序个数

4、和最大连续子数组

5、找出两个数组的中位数

6、在点集中找到三个点是构成的三角形周长最小

7、求出满足距离要求的点对数

链接：https://pan.baidu.com/s/1wsqjpB8Xgzgw_GnSRRP40w
提取码：k1yp