【算法题】判断一颗二叉树是否对称_给一个二叉树检查是否轴对称

---

theme: nico

一起养成写作习惯！这是我参与「掘金日新计划 · 4 月更文挑战」的第8天，点击查看活动详情。

大家好，我是前端西瓜哥。今天做一道比较基础的二叉树算法题。

题目

给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例1：

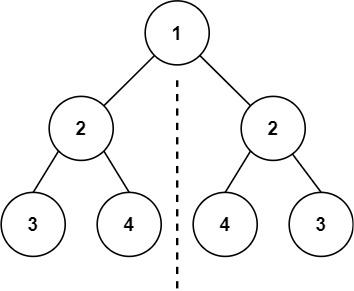
输入：root = [1,2,2,3,4,4,3]
输出：true
1
2

示例 2：

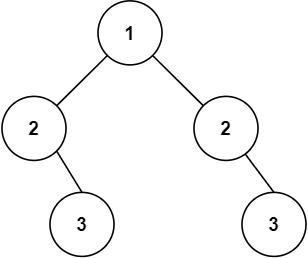
输入：root = [1,2,2,null,3,null,3]
输出：false
1
2

本题 LeetCode 对应地址：

https://leetcode-cn.com/problems/symmetric-tree/

解法

如果你熟练写二叉树的先序、中序、后序遍历的递归写法套路，再看这题，可能一时不太能想到思路。

我一开始做这道题就是这样，我会将注意力放在一个节点上，尝试在上面写出花来。

但对这题来说并不受用，一开始或许可以对比根节点的左右子节点，但左右子节点的后稷的子节点就不好取出来对比了。

对于这题，我们需要给递归函数，传入两个节点。

function isSymmetric(root) {
  if (!root) return true;
  return compare(root.left, root.right);
};

function compare(left, right) {
  if (!left && !right) return true;
  if (!left || !right) return false;
  return left.val === right.val &&
    compare(left.left, right.right) &&
    compare(left.right, right.left);
}
1
2
3
4
5
6
7
8
9
10
11
12

compare 递归函数接收两个节点，如果这两个节点对称，返回 true，否则返回 false。

首先是 left 和 right 都为 null 的情况，属于对称，返回 null。

null 的情况需要在最前方判断，因为后面我们要使用 left.val 的语法，如果 left 是 null，会报错。

然后就是 left 或 right 其中一个为 null 另一个不为 null 的情况。

因为前面的 if (!left && !right) return true; 如果不符合条件，代码往后走时，left 和 right 至少有一个不为 null。所以只要有 left 或 right 有一个 null，就说明一个为 null 一个不为 null，说明不对称，返回 false。

if (!left && !right) return true;
// 代码能运行到这里，说明 left 和 right 至少有一个为 null
if (!left || !right) return false;
1
2
3

如果你想更容易理解，可以改成这样子：

if (!left && !right) return true;
// 下面代码没有利用上面的条件判断
if (left && !right) return false;
if (!left && right) return false;
1
2
3
4

最后 left 和 right 都不为 null 的情况，我们需要对比以下节点

• left 和 right
• left.left 和 right.right
• left.right 和 right.left

当这些都为 true 的话，递归函数就返回 true；否则返回 false。

这里的 && 操作符支持短路运行，当前面的条件不符合，后面的函数就不会执行，起到剪枝的效果。

LeetCode 官方递归解法的缺陷

我看了一下 LeetCode 的官方解法，发现它有个地方和我的不一样：

function isSymmetric(root) {
  return compare(root, root);
};

function compare(left, right) {
  // 实现同上
}
1
2
3
4
5
6
7

就是它是直接将 root 和 root 对比，我初一看，觉得挺优雅的，不需要像我一样写额外的 root 为空的判断。

但我很快发现了不妥的地方，那就是这种写法，在二叉树是对称的情况下，所有节点都要被访问两次。

虽然从时间复杂度上来说，它也是 O(n) 的量级，但从实际情况是，LeetCode 官方解法在二叉树对称情况下，花费的时间我的解法的两倍。

如果二叉树不对称，因为 && 运算的短路特性，耗时倒和我的解法没有太大区别。

我是前端西瓜哥，分享前端和算法知识，欢迎关注我。