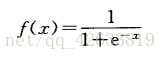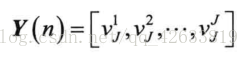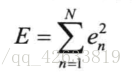神经网络学习（3）————BP神经网络以及python实现_可调节层数的bp神经网络

一、BP神经网络结构模型       

        BP算法的基本思想是，学习过程由信号的正向传播和误差的反向传播俩个过程组成，输入从输入层输入，经隐层处理以后，传向输出层。如果输出层的实际输出和期望输出不符合，就进入误差的反向传播阶段。误差反向传播是将输出误差以某种形式通过隐层向输入层反向传播，并将误差分摊给各层的所有单元，从而获得各层单元的误差信号，这个误差信号就作为修正个单元权值的依据。知道输出的误差满足一定条件或者迭代次数达到一定次数。

层与层之间为全连接，同一层之间没有连接。结构模型如下图所示。

        使用的传递函数sigmoid可微的特性使他可以使用梯度下降法。所以，在隐层函数中使用sigmoid函数作为传递函数，在输出层采用线性函数作为传递函数。

输入向量、隐层输出向量、最终输出向量、期望输出向量：

X=（x1,x2,x3……xn），其中图中x0是为隐层神经元引入阈值设置的;

Y=(y1,y2,y3……ym),其中图中y0是为输出神经元引入阈值设置的;

O=(o1,o2,o3……ol)

D=（d1,d2,d3……dl）

输出层的输入是隐层的输出，隐层的输入是输入层的输出，计算方法和单层感知器的计算方法一样。

单极性Sigmoid函数：

双极性sigmoid函数：

二、BP神经网络的学习算法

        标准BP神经网络沿着误差性能函数梯度的反方向修改权值，原理与LMS算法比较类似，属于最速下降法。此外还有以下改进算法，如动量最速下降法，拟牛顿法等。

    最速下降法又称为梯度下降法。LMS算法就是最小均方误差算法。LMS算法体现了纠错原则，与梯度下降法本质上没有区别，梯度下降法可以求目标函数的极小值，如果将目标函数取为均方误差，就得到了LMS算法。

       梯度下降法原理：对于实值函数F(x)，如果函数在某点x0处有定义且可微，则函数在该点处沿着梯度相反的方向下降最快，因此，使用梯度下降法时，应首先计算函数在某点处的梯度，再沿着梯度的反方向以一定的步长调整自变量的值。其中实值函数指的是传递函数，自变量x指的是上一层权值和输入值的点积作为的输出值。

        网络误差定义：

   

   

三层BP网络算法推导：

1、变量定义

网络的实际输出：

1. 信号正向传播

1. 误差信号反向传播

首先误差反向传播首先经过输出层，所以首先调整隐含层和输出层之间的权值。

然后对输入神经元和隐层神经元的误差进行调整。

权值矩阵的调整可以总结为:

    权值调整量det(w)=学习率*局部梯度*上一层输出信号。

BP神经网络的复杂之处在于隐层输入层、隐层和隐层之间的权值调整时，局部梯度的计算需要用到上一步计算的结果，前一层的局部梯度是后一层局部梯度的加权和。

 

训练方式：

1. 串行方式：网络每获得一个新样本，就计算一次误差并更新权值，直到样本输入完毕。

2. 批量方式：网络获得所有的训练样本，计算所有样本均方误差的和作为总误差；

在串行运行方式中，每个样本依次输入，需要的存储空间更少，训练样本的选择是随机的，可以降低网络陷入局部最优的可能性。

批量学习方式比串行方式更容易实现并行化。由于所有样本同时参加运算，因此批量方式的学习速度往往远优于串行方式。

 

BP神经网络的优点：

1. 非线性映射能力
2. 泛化能力  
3. 容错能力  允许输入样本中带有较大误差甚至个别错误。反应正确规律的知识来自全体样本，个别样本中的误差不能左右对权矩阵的调整。

 

BP神经网络的局限性：

    梯度下降法的缺陷：

1. 目标函数必须可微；
2. 如果一片区域比较平坦会花费较多时间进行训练；
3. 可能会陷入局部极小值，而没有到达全局最小值；（求全局极小值的目的是为了实现误差的最小值）

BP神经网络的缺陷：

1. 需要的参数过多，而且参数的选择没有有效的方法。确定一个BP神经网络需要知道：网络的层数、每一层神经元的个数和权值。权值可以通过学习得到，如果，隐层神经元数量太多会引起过学习，如果隐层神经元个数太少会引起欠学习。此外学习率的选择也是需要考虑。目前来说，对于参数的确定缺少一个简单有效的方法，所以导致算法很不稳定；
2. 属于监督学习，对于样本有较大依赖性，网络学习的逼近和推广能力与样本有很大关系，如果样本集合代表性差，样本矛盾多，存在冗余样本，网络就很难达到预期的性能；
3. 由于权值是随机给定的，所以BP神经网络具有不可重现性；

 

梯度下降法（最速下降法的改进）：

    针对算法的不足出现了几种BP算法的改进。

1. 动量法

动量法是在标准BP算法的权值更新阶段引入动量因子α（0<α<1）,使权值修正具有一定惯性，可以看出，在原有的权值调整公式中，加入了动量因子以及上一次的权值改变量。加入的动量项表示本次权值的更新方向和幅度，不但与本次计算所得的梯度有关，还与上一次更新的方向和幅度有关。动量项反映了以前积累的调整经验，对于t时刻的调整起到了阻尼作用。当误差曲面出现骤然起伏时，可减小震荡趋势，提高训练速度。

1. 调节学习率法

在平缓区域希望学习率大一点减小迭代次数，在坑凹处希望学习率小一点，较小震荡。所以，为了加速收敛过程，希望自适应改变学习率，在该大的时候大，在该小的时候小。

学习率可变的BP算法是通过观察误差的增减来判断的，当误差以减小的方式区域目标时，说明修正方向是正确的，可以增加学习率；当误差增加超过一定范围时，说明前一步修正进行的不正确，应减小步长，并撤销前一步修正过程。学习率的增减通过乘以一个增量/减量因子实现：

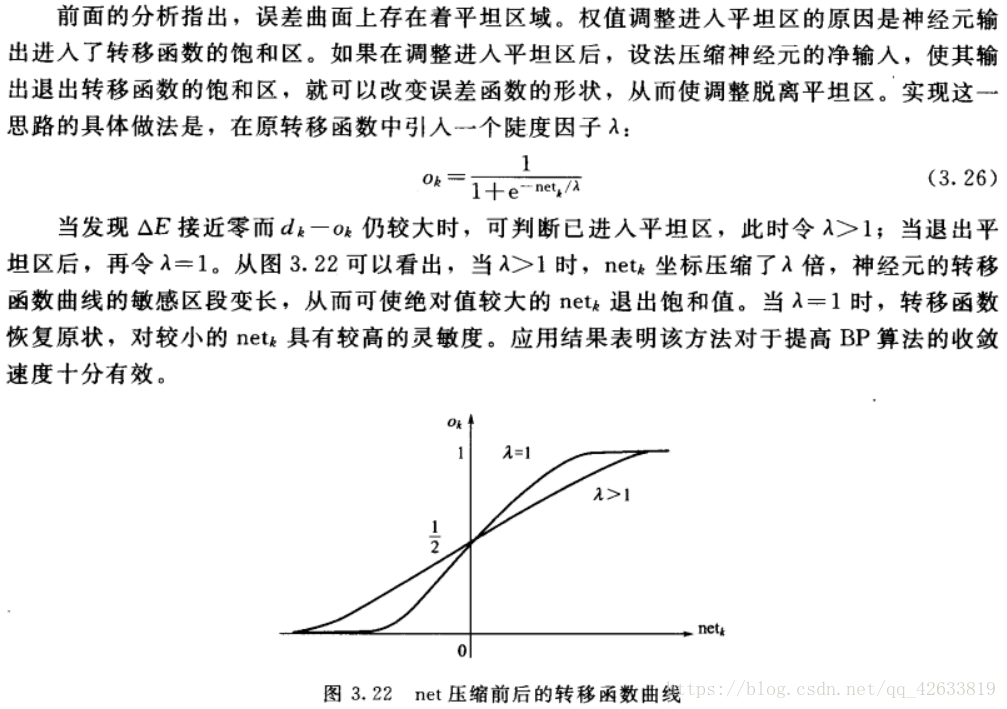
1. 引入陡度因子。

 

 

BP神经网络的设计：

   BP神经网络采用有监督学习。解决具体问题时，首先需要一个训练集。然后神经网络的设计主要包括网络层数、输入层节点数、隐层节点数、输出层节点数、以及传输函数、训练方法、训练参数。

 

（一）输入输出数据的预处理：尺度变换。尺度变化也称为归一化或者标准化，是指变换处理将网络的输入、输出数据限制在[0,1]或者[-1,1]区间内。进行变换的原因是，（1）网络的各个输入数据常常具有不同的物理意义和不同的量纲。尺度变换使所有分量都在一个区间内变化，从而使网络训练一开始就给各输入分量以同等重要的地位；（2）BP神经网络神经元均采用sigmoid函数，变换后可防止因净输入的绝对值过大而使神经元输出饱和，继而使权值调整进入误差曲面的平坦区；（3）sigmoid函数输出在区间[0,1]或者[-1,1]内，如果不对期望输出数据进行变换处理，势必使数值大的分量绝对误差大，数值小的分量绝对误差小。

（二）神经网络结构设计

1）网络层数  BP神经网络最多只需要俩个隐层，在设计的时候一般先只考虑设一个隐层，当一个隐层的节点数很多但是依然不能改善网络情况时，才考虑增加一个隐层。经验表明，如果在第一个隐层较多的节点数，第二个隐层较少的节点数，可以改善网络性能。

2）输入层节点数  输入层节点数取决于输入向量的维数。应用神经网络解决实际问题时，首先应从问题中提炼出一个抽象模型。如果输入的是64*64的图像，则输入向量应为图像中左右的像素形成的4096维向量。如果待解决的问题是二院函数拟合，则输入向量应为二维向量。

3）隐层节点数设计  隐含节点数对BP神经网络的性能有很大影响，一般较多的隐含层节点数可以带来更好的性能，但是导致训练时间过长。通常是采用经验公式给出估计值：

4）输出层神经元个数  

5）传递函数的选择  一般隐层选择sigmoid函数，输出层选择线性函数。如果也使用sigmoid函数，则输出值将会被限制在（0,1）或者（-1,1）之间。

6）训练方法的选择  一般来说，对于包含数百个权值的函数逼近网络，使用LM算法收敛速度最快，均方误差也小，但是LM算法对于模式识别相关问题的处理能力较弱，且需要较大的存储空间。对于模式识别问题，使用RPROP算法能收到较好的效果。SCG算法对于模式识别和函数逼近都有较好的性能表现。串行方式需要更小的存储空间，且输入样本具有一定随机性，可以避免陷入局部最优。批量方式的误差收敛条件非常简单，训练速度快。

 

三、python实现加动量法改进

# -*- coding: utf-8 -*-
"""
Created on Mon Oct  1 22:15:54 2018
@author: Heisenberg
"""
import numpy as np
import math
import random
import string
import matplotlib as mpl
import matplotlib.pyplot as plt
 
#random.seed(0)  #当我们设置相同的seed，每次生成的随机数相同。如果不设置seed，则每次会生成不同的随机数
                #参考https://blog.csdn.net/jiangjiang_jian/article/details/79031788
 
#生成区间[a,b]内的随机数
def random_number(a,b):
    return (b-a)*random.random()+a
 
#生成一个矩阵，大小为m*n,并且设置默认零矩阵
def makematrix(m, n, fill=0.0):
    a = []
    for i in range(m):
        a.append([fill]*n)
    return a
 
#函数sigmoid(),这里采用tanh，因为看起来要比标准的sigmoid函数好看
def sigmoid(x):
    return math.tanh(x)
 
#函数sigmoid的派生函数
def derived_sigmoid(x):
    return 1.0 - x**2
 
#构造三层BP网络架构
class BPNN:
    def __init__(self, num_in, num_hidden, num_out):
        #输入层，隐藏层，输出层的节点数
        self.num_in = num_in + 1  #增加一个偏置结点
        self.num_hidden = num_hidden + 1   #增加一个偏置结点
        self.num_out = num_out
        
        #激活神经网络的所有节点（向量）
        self.active_in = [1.0]*self.num_in
        self.active_hidden = [1.0]*self.num_hidden
        self.active_out = [1.0]*self.num_out
        
        #创建权重矩阵
        self.wight_in = makematrix(self.num_in, self.num_hidden)
        self.wight_out = makematrix(self.num_hidden, self.num_out)
        
        #对权值矩阵赋初值
        for i in range(self.num_in):
            for j in range(self.num_hidden):
                self.wight_in[i][j] = random_number(-0.2, 0.2)
        for i in range(self.num_hidden):
            for j in range(self.num_out):
                self.wight_out[i][j] = random_number(-0.2, 0.2)
    
        #最后建立动量因子（矩阵）
        self.ci = makematrix(self.num_in, self.num_hidden)
        self.co = makematrix(self.num_hidden, self.num_out)        
        
    #信号正向传播
    def update(self, inputs):
        if len(inputs) != self.num_in-1:
            raise ValueError('与输入层节点数不符')
            
        #数据输入输入层
        for i in range(self.num_in - 1):
            #self.active_in[i] = sigmoid(inputs[i])  #或者先在输入层进行数据处理
            self.active_in[i] = inputs[i]  #active_in[]是输入数据的矩阵
            
        #数据在隐藏层的处理
        for i in range(self.num_hidden - 1):
            sum = 0.0
            for j in range(self.num_in):
                sum = sum + self.active_in[i] * self.wight_in[j][i]
            self.active_hidden[i] = sigmoid(sum)   #active_hidden[]是处理完输入数据之后存储，作为输出层的输入数据
            
        #数据在输出层的处理
        for i in range(self.num_out):
            sum = 0.0
            for j in range(self.num_hidden):
                sum = sum + self.active_hidden[j]*self.wight_out[j][i]
            self.active_out[i] = sigmoid(sum)   #与上同理
            
        return self.active_out[:]
    
    #误差反向传播
    def errorbackpropagate(self, targets, lr, m):   #lr是学习率， m是动量因子
        if len(targets) != self.num_out:
            raise ValueError('与输出层节点数不符！')
            
        #首先计算输出层的误差
        out_deltas = [0.0]*self.num_out
        for i in range(self.num_out):
            error = targets[i] - self.active_out[i]
            out_deltas[i] = derived_sigmoid(self.active_out[i])*error
        
        #然后计算隐藏层误差
        hidden_deltas = [0.0]*self.num_hidden
        for i in range(self.num_hidden):
            error = 0.0
            for j in range(self.num_out):
                error = error + out_deltas[j]* self.wight_out[i][j]
            hidden_deltas[i] = derived_sigmoid(self.active_hidden[i])*error
        
        #首先更新输出层权值
        for i in range(self.num_hidden):
            for j in range(self.num_out):
                change = out_deltas[j]*self.active_hidden[i]
                self.wight_out[i][j] = self.wight_out[i][j] + lr*change + m*self.co[i][j]
                self.co[i][j] = change
                
        #然后更新输入层权值
        for i in range(self.num_in):
            for i in range(self.num_hidden):
                change = hidden_deltas[j]*self.active_in[i]
                self.wight_in[i][j] = self.wight_in[i][j] + lr*change + m* self.ci[i][j]
                self.ci[i][j] = change
                
        #计算总误差
        error = 0.0
        for i in range(len(targets)):
            error = error + 0.5*(targets[i] - self.active_out[i])**2
        return error
 
    #测试
    def test(self, patterns):
        for i in patterns:
            print(i[0], '->', self.update(i[0]))
    #权重
    def weights(self):
        print("输入层权重")
        for i in range(self.num_in):
            print(self.wight_in[i])
        print("输出层权重")
        for i in range(self.num_hidden):
            print(self.wight_out[i])
            
    def train(self, pattern, itera=100000, lr = 0.1, m=0.1):
        for i in range(itera):
            error = 0.0
            for j in pattern:
                inputs = j[0]
                targets = j[1]
                self.update(inputs)
                error = error + self.errorbackpropagate(targets, lr, m)
            if i % 100 == 0:
                print('误差 %-.5f' % error)
    
#实例
def demo():
    patt = [
            [[1,2,5],[0]],
            [[1,3,4],[1]],
            [[1,6,2],[1]],
            [[1,5,1],[0]],
            [[1,8,4],[1]]
            ]
    #创建神经网络，3个输入节点，3个隐藏层节点，1个输出层节点
    n = BPNN(3, 3, 1)
    #训练神经网络
    n.train(patt)
    #测试神经网络
    n.test(patt)
    #查阅权重值
    n.weights()
 
     
if __name__ == '__main__':
    demo()
 

计算结果：