主题模型：LDA原理详解与应用_lda模型原理

LDA算法简介：

LDA是一种基于贝叶斯思想的无监督的聚类算法，广泛用于文本聚类，文本分析，文本关键词等场景。具体的，算法 的输入是一个文档的集合D={d1, d2, d3, ... , dn}，同时还需要主题Topic的类别数量m；然后会算法会将每一篇文档 di 在 所有Topic上的一个概率值p；这样每篇文档都会得到一个概率的集合di=(dp1，dp2，..., dpm), 表示文档di在m个topic上的概率值；同样的文档中的所有词也会求出 它对应每个Topic的概率，wi = （wp1，wp2，wp3，...，wpm）；这样就得到了两个矩阵，一个文档到Topic，一个词到Topic。

其核心公示为：

p(w|d) = p(w|t)*p(t|d)

直观的看这个公式，就是以Topic作为中间层，可以通过当前的θd和φt给出了文档d中出现单词w的概率。其中p(t|d)利用θd计算得到，p(w|t)利用φt计算得到。

　　实际上，利用当前的θd和φt，我们可以为一个文档中的一个单词计算它对应任意一个Topic时的p(w|d)，然后根据这些结果来更新这个词应该对应的topic。然后，如果这个更新改变了这个单词所对应的Topic，就会反过来影响θd和φt。

　　LDA算法开始时，先随机地给θd和φt赋值（对所有的d和t）。然后上述过程不断重复，最终收敛到的结果就是LDA的输出。

这样LDA算法，就将文档和词，投射到了一组Topic上，试图通过Topic找出文档与词间，文档与文档间，词于词之间潜在的关系；由于LDA属于无监督算法，每个Topic并不会要求指定条件，但聚类后，通过统计出各个Topic上词的概率分布，那些在该Topic上概率高的词，能非常好的描述该Topic的意义。

LDA算法原理：

在讲LDA模型之前，会先介绍下 Unigram Model （词袋模型）、Bayes Unigram Model（贝叶斯词袋模型），以及PLSA 概率潜在语义分析，这些算法工作是LDA模型的思想起源。

1.Unigram Model （词袋模型）

 LDA既然是聚类算法，而聚类算法大多数时候，都在寻找两个东西的相似度。

最开始，大家想要判断两篇文档是否相似，最简单直接的方法就是看文档里出现的词是否一样，其个数是否相近。于Unigram Model（词袋模型）就是实现这样的思路设计的。所以为了得到文档集合中，所有文档的共性的规律，词袋模型，假设：一篇文档生成的过程就是 独立的抛一个具有M面的骰子（M是所有词的个数），N次（N是该文档里词的个数），这样文档的生成，刚好可以看作是个多项式分布：

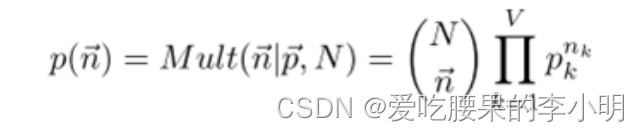
文档集合中，每个词出现的概率就是要求的参数，通过EM算法可以确定下来，这样就得到了模型。

2. Bayes Unigram Model（贝叶斯词袋模型）

词袋模型是频率学派，简单的认为文档里每个词出现的概率是个定数（即骰子的每个面的概率），但Bayes学派不这么认为，他们认为这些概率应该是一个随机过程产生的，于是生成一篇文档的过程可以描述为：先随机抽取一个M面的骰子（每个词出现的概率也是一个分布）， 再用这个骰子独立抛N次。那么这个模型的分布如下：

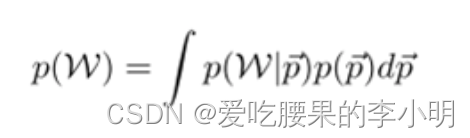
是多项式分布，为了方便计算，假设为Dirichlet分布，它是多项式分布的共轭分布。

共轭分布：

共轭分布(conjugate distribution)的概率中一共涉及到三个分布：先验、似然和后验，如果由先验分布和似然分布所确定的后验分布与该先验分布属于同一种类型的分布，则该先验分布为似然分布的共轭分布，也称为共轭先验。

假设变量xx服从分布P(x|θ)P(x|θ)，其观测样本为X={x1,x2,...,xm}X={x1,x2,...,xm}，参数θθ服从先验分布Π(θ)Π(θ)。那么后验分布为
  P(θ|X)=Π(θ)P(X|θ)P(X)
如果后验分布P(θ|X)P(θ|X)与先验分布Π(θ)Π(θ)是同种类型的分布，则称先验分布Π(θ)Π(θ)为似然分布P(X|θ)P(X|θ)的共轭分布。
  比较常用的几个例子有：高斯分布是高斯分布的共轭分布，Beta分布是二项分布的共轭分布，Dirichlet分布是多项分布的共轭分布。

Dirichlet 分布：比如 抛了100次骰子，得到6个面的一个概率，记为一个实验，重复这个实验100次，那么这100次的实验中，这6个面的概率的概率分布，就是Dirichlet分布，它是分布之上的分布。

例如：1点（骰子六个面之一） 在这100次实验（每个实验抛100次） 是 0.15的概率为 0.12，实际我们这么想，100次实验中，有12次，1点在一个实验内出现了15次，可以看作是总共抛10000次，1点出现15×12=180次。这10000次实验，视为一个大的多项式分布，于是可以得出他们有相同的概率分布公式，这就是前面所提到的共轴分布，且有如下性质：

                            先验的Dirichlet分布+多项式分布 = 后验的Dirichlet分布

上述的例子中，你会发现，它与我们的Bayes Unigram Model（贝叶斯词袋模型）已经很相似了。一个实验里的100次抛骰子，可以看作是先验的Dirichlet分布，也就是模型中确定骰子各个面概率的那个随机过程，而重复这个这个实验100次，可以看作是后面的根据这个骰子确定文档的一个过程。

Dirichlet分布还有一个重要的性质，它的最大似然估计可以通过如下公式，证明过程有些复杂，暂不推导了：

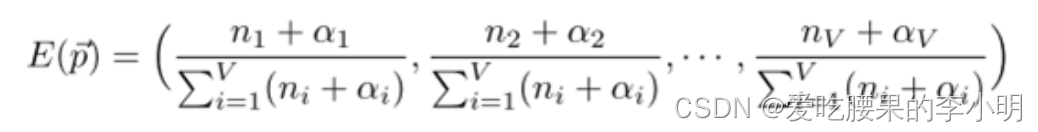
 3. PLSA潜在语义分析

在文本聚类的时候，常常会遇到这样一种问题：例如在NBA的相关新闻中提到“石佛”，和提到“邓肯”它们应该是指的同一个人，确实两个不同的词；而另一篇关于教育的新闻里也提到了“邓肯”，但此“邓肯”非彼“邓肯”，它可能指的是美国教育部部长“阿恩·邓肯”；而这两篇NBA新闻和一篇教育新闻，很可能就被错误的聚类了。

      于是，可以发现词在不同的语义环境下，同一个词可能表达不同意思，而同一个意思可能产生不同的词。PLSA潜在语义分析，就是为了解决这样的问题。它在文档和词之间加了一层主题（Topic），先让文档和主题产生关联，再在主题中寻找词的概率分布。

      PLSA模型将文档的生成这样设计：第一步，我们抛一个有H面的骰子，每个面代表一个主题，各个面概率不一，得到一个主题；第二步，这个主题又对应了一个有T个面的骰子，每个面代表一个词，抛这骰子N次，得到一篇文章。其实我觉得这个模型可以看作是两个词袋模型的组合，第一个做一次，确定主题，第二个重复独立做N词，确定文章。下面是一个直观图（借用LDA数学八卦的图了）：

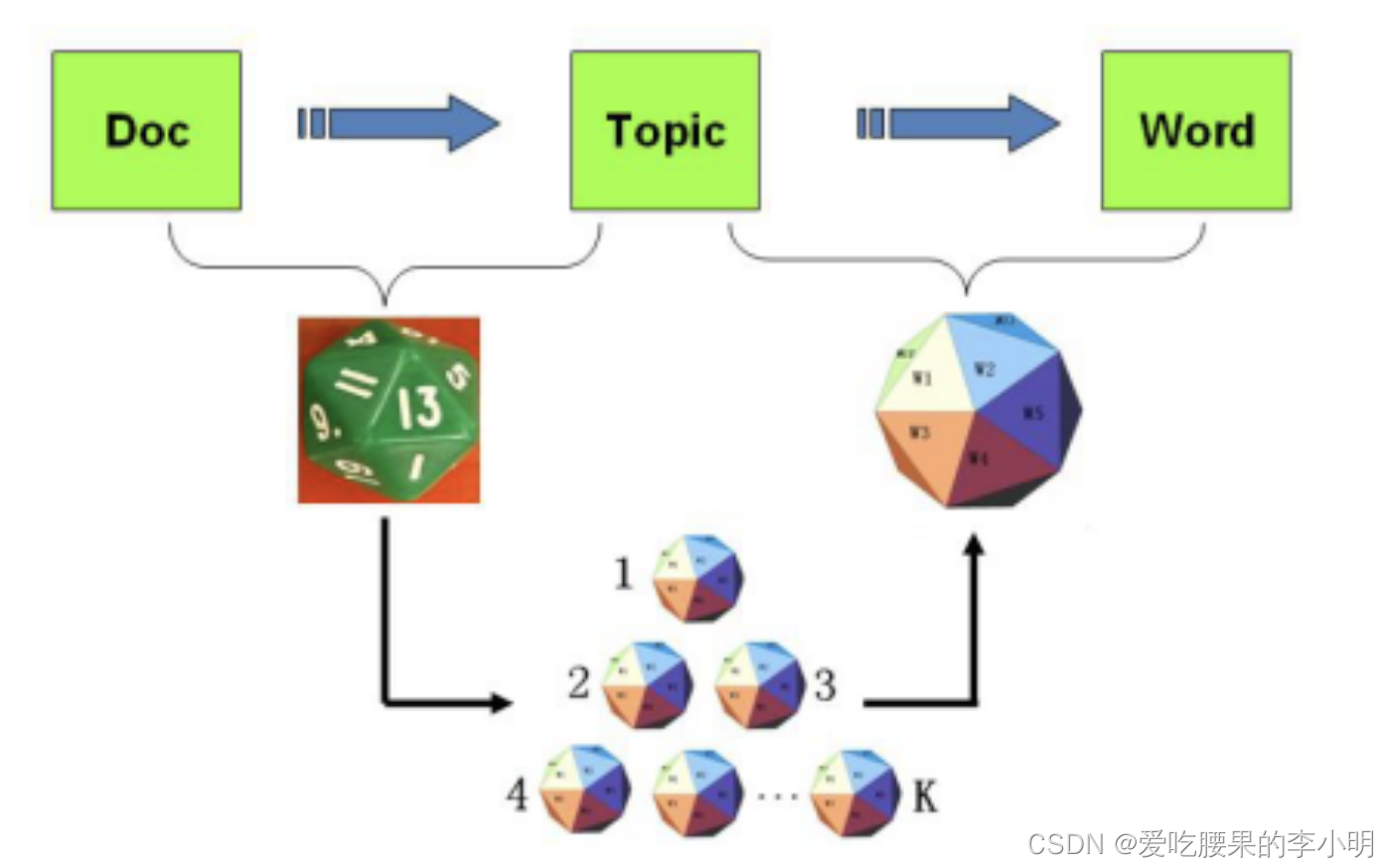
 这样概率分布公式如下：

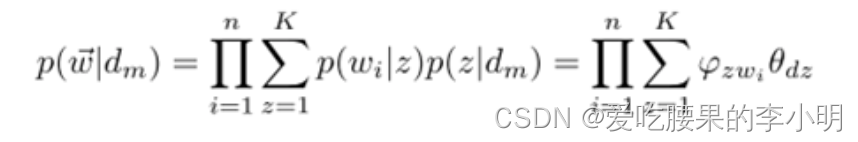
 4. LDA主题聚类模型

这时Bayes学派的朋友们又出现，历史是如此的相似，他们又对PLSA下手了，认为PLSA里面的两种骰子（产生主题的骰子和主题对应词的骰子），各个面的概率都不应该是确定，应该由一个随机过程来得出。于是让PLSA的两个词袋模型，变成两个Bayes词袋模型，就是LDA了

      前面已经介绍了，Bayes词袋模型的概率分布是一个Dirichlet 同轴分布，LDA 的整个物理过程实际就是两个Dirichlet 同轴分布，而 LDA 模型的参数估计也就出来了，通过那个重要的性质，如下：

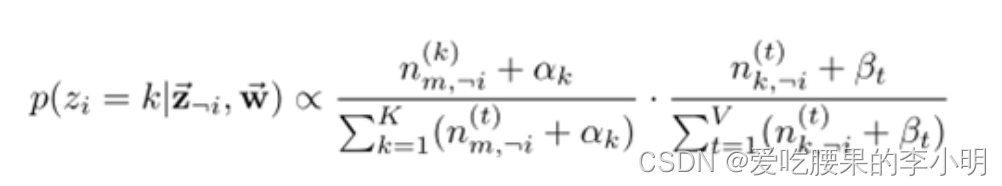
 LDA算法设计与Gibbs Sampling

算法步骤：

      1. 对文档集合中的每篇文档d，做分词，并过滤掉无意义词，得到语料集合W = {w1, w2, …, wx}。
      2. 对这些词做统计，得到 p（wi|d）。
      3. 为语料集合W中的每个 wi ，随机指定一个主题 t，作为初始主题。
      4. 通过 Gibbs Sampling 公式， 重新采样 每个 w 的所属 主题t， 并在语料中更新 直到Gibbs Sampling 收敛。
      收敛以后得到 主题-词 的概率矩阵，这个就是LDA矩阵，而 文档-主题的的概率矩阵也是能得到的，统计后，就能能得到文档-主题的概率分布。

      Gibbs Sampling 公式：
      Gibbs Sampling 公式，可以用于计算 某x维度的空间中，两个平行点之间转移的概率。 比如在 二维空间（x, y平面），点a（x1，y1） 转移到 b（x1，y2）的概率记为P，P（a ->b） = p(y2|x1 )

      于是上述中第4步，可以视为我们将一个词对应的 文档和Topic的概率 看作是一个点在二维平面里的两个维度，词在不同的文档和不同的主题里，通过Gibbs Sampling公式，不断的转移（即重新采样），直至收敛。 下面是Gibbs Sampling公式收敛的一个图，可以给大家一个直观印象（来自LDA数学八卦）。

一个例子

Suppose you have the following set of sentences:

• I like to eat broccoli and bananas.
• I ate a banana and spinach smoothie for breakfast.
• Chinchillas and kittens are cute.
• My sister adopted a kitten yesterday.
• Look at this cute hamster munching on a piece of broccoli.

What is latent Dirichlet allocation? It’s a way of automatically discovering topics that these sentences contain. For example, given these sentences and asked for 2 topics, LDA might produce something like

• Sentences 1 and 2: 100% Topic A
• Sentences 3 and 4: 100% Topic B
• Sentence 5: 60% Topic A, 40% Topic B
• Topic A: 30% broccoli, 15% bananas, 10% breakfast, 10% munching, … (at which point, you could interpret topic A to be about food)
• Topic B: 20% chinchillas, 20% kittens, 20% cute, 15% hamster, … (at which point, you could interpret topic B to be about cute animals)

　　上面关于sentence 5的结果，可以看出来是一个明显的概率类型的聚类结果（sentence 1和2正好都是100%的确定性结果）。

　　再看例子里的结果，除了为每句话得出了一个概率的聚类结果，而且对每个Topic，都有代表性的词以及一个比例。以Topic A为例，就是说所有对应到Topic A的词里面，有30%的词是broccoli。在LDA算法中，会把每一个文档中的每一个词对应到一个Topic，所以能算出上面这个比例。这些词为描述这个Topic起了一个很好的指导意义，我想这就是LDA区别于传统文本聚类的优势吧。

所以LDA要干的事情简单来说就是为一堆文档进行聚类（所以是非监督学习），一种topic就是一类，要聚成的topic数目是事先指定的。聚类的结果是一个概率，而不是布尔型的100%属于某个类。