devbox
很楠不爱3
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

【C语言】——十大排序算法_c语言十大算法

作者：很楠不爱3 | 2024-03-21 03:18:57

赞

踩

c语言十大算法

文章目录

  • 写在前面
  • 一、`【冒泡排序算法】`
  • 二、`【选择排序算法】`
  • 三、`【插入排序算法】`
  • 四、`【希尔排序算法】`
  • 五、`【归并排序算法】`
  • 六、`【快速排序算法】`
  • 七、`【堆排序算法】`
  • 八、`【计数排序算法】`
  • 九、`【计数排序算法】`
  • 十、`【计数排序算法】`
  • 写在最后

写在前面

  • 学了算法之后相信大家还需要整理一份关于算法的笔记，希望这篇文章能给大家带来一些启发和帮助。学习算法就是学习解决问题思想，在面对一个问题要利用算法的思维来思考会对解题有很大的帮助。

一、【冒泡排序算法】

冒泡排序，是一种计算机科学领域的较简单的排序算法。
它重复地走访过要排序的元素列，依次比较两个相邻的元素，如果顺序（如从大到小、首字母从Z到A）错误就把他们交换过来。走访元素的工作是重复地进行直到没有相邻元素需要交换，也就是说该元素列已经排序完成。
这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端（升序或降序排列），就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样，故名“冒泡排序”。

在这里插入图片描述

【源程序代码】

#include <stdio.h>
#define ARR_LEN 255 /*数组长度上限*/
#define elemType int /*元素类型*/

/* 冒泡排序 */
/* 1. 从当前元素起，向后依次比较每一对相邻元素，若逆序则交换 */
/* 2. 对所有元素均重复以上步骤，直至最后一个元素 */
/* elemType arr[]: 排序目标数组; int len: 元素个数 */
void bubbleSort(elemType arr[], int len)
{
	elemType temp;
	int i, j;
	for (i = 0; i < len - 1; i++) /* 外循环为排序趟数，len个数进行len-1趟 */
	{
		for (j = 0; j < len - 1 - i; j++)
		{ /* 内循环为每趟比较的次数，第i趟比较len-i次 */
			if (arr[j] > arr[j + 1])
			{ /* 相邻元素比较，若逆序则交换（升序为左大于右，降序反之） */
				temp = arr[j];
				arr[j] = arr[j + 1];
				arr[j + 1] = temp;
			}
		}
	}

}

int main(void)
{
	elemType arr[ARR_LEN] = { 3,5,1,-7,4,9,-6,8,10,4 };
	int len = 10;
	int i;

	bubbleSort(arr, len);
	printf("\n\n数组排序之后输出】\n\n");
	for (i = 0; i < len; i++)
		printf("%d\t", arr[i]);
	putchar('\n');

	return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41

【运行结果】
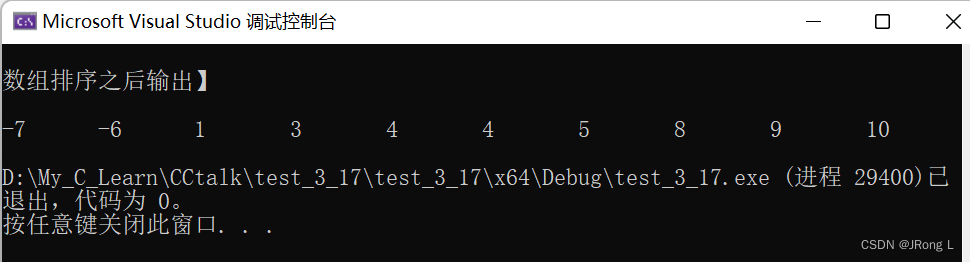
在这里插入图片描述

二、【选择排序算法】

选择排序是一种简单直观的排序算法。
它的工作原理是：第一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，然后再从剩余的未排序元素中寻找到最小（大）元素，然后放到已排序的序列的末尾。以此类推，直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法。

在这里插入图片描述

【源程序代码】

#include <stdio.h>
int main()
{
    int i, j, t, a[11];    //定义变量及数组为基本整型
    printf("请输入10个数：\n");
    for (i = 1; i < 11; i++)
        scanf_s("%d", &a[i]);    //从键盘中输入要排序的10个数字
    for (i = 1; i <= 9; i++)
        for (j = i + 1; j <= 10; j++)
            if (a[i] > a[j])    //如果前一个数比后一个数大，则利用中间变量t实现两值互换
            {
                t = a[i];
                a[i] = a[j];
                a[j] = t;
            }
    printf("排序后的顺序是：\n");
    for (i = 1; i <= 10; i++)
        printf("%5d", a[i]);    //输出排序后的数组
    printf("\n");
    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21

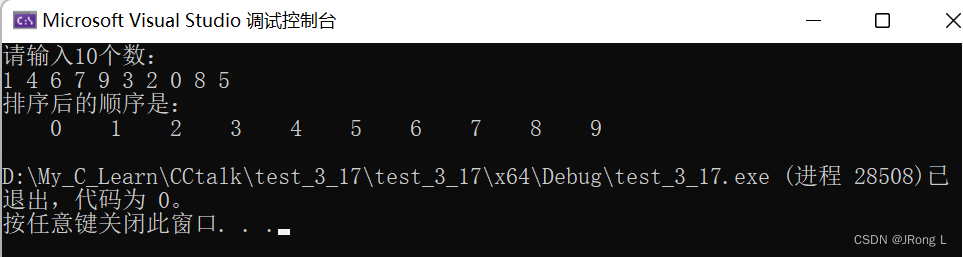
在这里插入图片描述

三、【插入排序算法】

插入排序，一般也被称为直接插入排序。
对于少量元素的排序，它是一个有效的算法。插入排序是一种最简单的排序方法，它的基本思想是将一个记录插入到已经排好序的有序表中，从而一个新的、记录数增1的有序表。在其实现过程使用双层循环，外层循环对除了第一个元素之外的所有元素，内层循环对当前元素前面有序表进行待插入位置查找，并进行移动。

在这里插入图片描述

【源程序代码】

#include <stdio.h>
//自定义的输出函数
void print(int a[], int n, int i) {
	printf("%d:", i);
	for (int j = 0; j < 8; j++) {
		printf("%5d", a[j]);
	}
	printf("\n");
}
//直接插入排序函数
void InsertSort(int a[], int n)
{
	for (int i = 1; i < n; i++)
	{
		if (a[i] < a[i - 1])
		{//若第 i 个元素大于 i-1 元素则直接插入；反之，需要找到适当的插入位置后在插入。
			int j = i - 1;
			int x = a[i];
			while (j > -1 && x < a[j])
			{  //采用顺序查找方式找到插入的位置，在查找的同时，将数组中的元素进行后移操作，给插入元素腾出空间
				a[j + 1] = a[j];
				j--;
			}
			a[j + 1] = x;      //插入到正确位置
		}
		print(a, n, i);//打印每次排序后的结果
	}
}

int main()
{
	int a[8] = { 31,12,17,45,26,84,99,67 };
	printf("\n\n【数组排序之后输出】\n\n");

	InsertSort(a, 8);

	return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38

【运行结果】
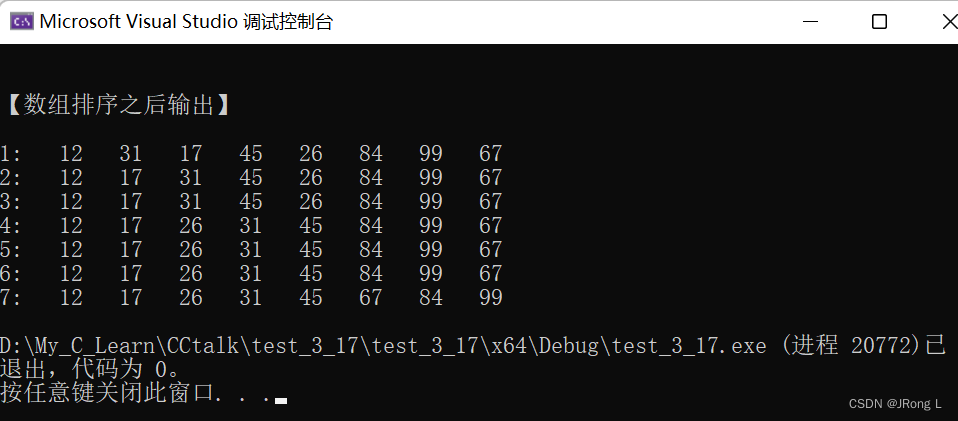
在这里插入图片描述

四、【希尔排序算法】

希尔排序是插入排序的一种又称“缩小增量排序”（Diminishing Increment Sort），是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因 D.L.Shell 于 1959 年提出而得名。
希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至 1 时，整个文件恰被分成一组，算法便终止。

在这里插入图片描述

【源程序代码】

#include<stdio.h>
#include<math.h>

#define MAXNUM 10

void main()
{
	void shellSort(int array[], int n, int t);//t为排序趟数
	int array[MAXNUM], i;
	printf("\n\n请输入10个数字:\n");
	for (i = 0; i < MAXNUM; i++)
		scanf_s("%d", &array[i]);
	shellSort(array, MAXNUM, (int)(log(MAXNUM + 1) / log(2)));//排序趟数应为log2(n+1)的整数部分

	printf("\n\n排序后输出结果为:\n");
	for (i = 0; i < MAXNUM; i++)
		printf("%d ", array[i]);

	printf("\n");
}

//根据当前增量进行插入排序
void shellInsert(int array[], int n, int dk)
{
	int i, j, temp;
	for (i = dk; i < n; i++)//分别向每组的有序区域插入
	{
		temp = array[i];
		for (j = i - dk; (j >= i % dk) && array[j] > temp; j -= dk)//比较与记录后移同时进行
			array[j + dk] = array[j];
		if (j != i - dk)
			array[j + dk] = temp;//插入
	}
}

//计算Hibbard增量
int dkHibbard(int t, int k)
{
	return (int)(pow(2, t - k + 1) - 1);
}

//希尔排序
void shellSort(int array[], int n, int t)
{
	void shellInsert(int array[], int n, int dk);
	int i;
	for (i = 1; i <= t; i++)
		shellInsert(array, n, dkHibbard(t, i));
}

//此写法便于理解，实际应用时应将上述三个函数写成一个函数。

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51

【运行结果】
在这里插入图片描述

五、【归并排序算法】

归并排序是建立在归并操作上的一种有效，稳定的排序算法，该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

在这里插入图片描述
【算法描述】

归并操作的工作原理如下：
第一步：申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
第二步：设定两个指针，最初位置分别为两个已经排序序列的起始位置
第三步：比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
重复步骤3直到某一指针超出序列尾，将另一序列剩下的所有元素直接复制到合并序列尾。

【源程序代码】

#include <stdlib.h>
#include <stdio.h>

void Merge(int sourceArr[], int tempArr[], int startIndex, int midIndex, int endIndex)
{
    int i = startIndex, j = midIndex + 1, k = startIndex;
    while (i != midIndex + 1 && j != endIndex + 1)
    {
        if (sourceArr[i] > sourceArr[j])
            tempArr[k++] = sourceArr[j++];
        else
            tempArr[k++] = sourceArr[i++];
    }
    while (i != midIndex + 1)
        tempArr[k++] = sourceArr[i++];
    while (j != endIndex + 1)
        tempArr[k++] = sourceArr[j++];
    for (i = startIndex; i <= endIndex; i++)
        sourceArr[i] = tempArr[i];
}

//内部使用递归
void MergeSort(int sourceArr[], int tempArr[], int startIndex, int endIndex)
{
    int midIndex;
    if (startIndex < endIndex)
    {
        midIndex = startIndex + (endIndex - startIndex) / 2;//避免溢出int
        MergeSort(sourceArr, tempArr, startIndex, midIndex);
        MergeSort(sourceArr, tempArr, midIndex + 1, endIndex);
        Merge(sourceArr, tempArr, startIndex, midIndex, endIndex);
    }
}

int main(int argc, char* argv[])
{
    int a[8] = { 50, 10, 20, 30, 70, 40, 80, 60 };
    int i, b[8];
    MergeSort(a, b, 0, 7);
    printf("\n\n【数组排序后输出结果】\n\n");
    for (i = 0; i < 8; i++)
        printf("%5d ", a[i]);
    printf("\n");

    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46

【运行结果】
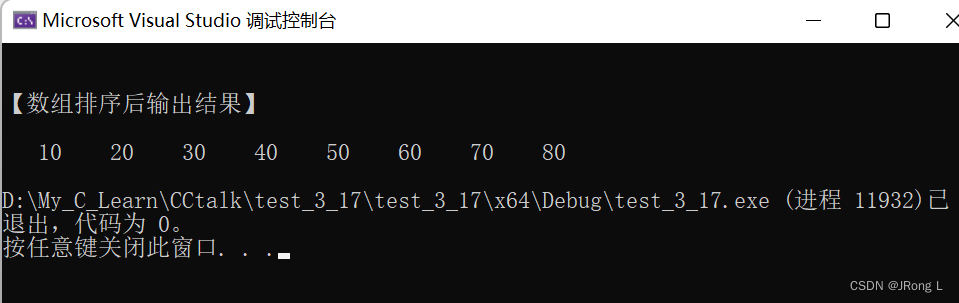
在这里插入图片描述

六、【快速排序算法】

快速排序是对冒泡排序的一种改进。
快速排序由C. A. R. Hoare在1960年提出。它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

在这里插入图片描述
排序流程
快速排序算法通过多次比较和交换来实现排序，其排序流程如下：
1、首先设定一个分界值，通过该分界值将数组分成左右两部分。
2、将大于或等于分界值的数据集中到数组右边，小于分界值的数据集中到数组的左边。此时，左边部分中各元素都小于或等于分界值，而右边部分中各元素都大于或等于分界值。
3、然后，左边和右边的数据可以独立排序。对于左侧的数组数据，又可以取一个分界值，将该部分数据分成左右两部分，同样在左边放置较小值，右边放置较大值。右侧的数组数据也可以做类似处理。
4、重复上述过程，可以看出，这是一个递归定义。通过递归将左侧部分排好序后，再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后，整个数组的排序也就完成了。

【源程序代码】

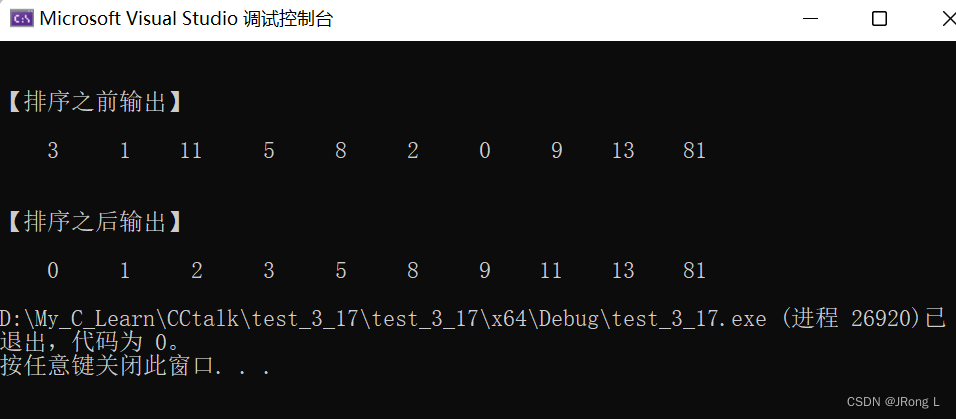
#include <stdio.h>

void quickSort(int arr[], int low, int high)
{
    int first = low;
    int last = high;
    int key = arr[first];
    if (low >= high)
        return;
    while (first < last)
    {
        while (first < last && arr[last] > key)
        {
            last--;
        }
        arr[first] = arr[last];

        while (first < last && arr[first] < key)
        {
            first++;
        }
        arr[last] = arr[first];
    }
    arr[first] = key;

    quickSort(arr, low, first - 1);
    quickSort(arr, first + 1, high);
}

int main()
{
    int i;
    int a[10] = { 3, 1, 11, 5, 8, 2, 0, 9, 13, 81 };

    printf("\n\n【排序之前输出】\n\n");
    for (i = 0; i < 10; i++)
        printf("%5d ", a[i]);
    printf("\n");

    quickSort(a, 0, 9);

    printf("\n\n【排序之后输出】\n\n");
    for (i = 0; i < 10; i++)
        printf("%5d ", a[i]);
    printf("\n");

    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48

【运行结果】
在这里插入图片描述

七、【堆排序算法】

堆排序是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。
堆排序（英语：Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

在这里插入图片描述
堆的操作：
在堆的数据结构中，堆中的最大值总是位于根节点（在优先队列中使用堆的话堆中的最小值位于根节点）。
堆中定义以下几种操作：
最大堆调整（Max Heapify）：将堆的末端子节点作调整，使得子节点永远小于父节点
创建最大堆（Build Max Heap）：将堆中的所有数据重新排序
堆排序（HeapSort）：移除位在第一个数据的根节点，并做最大堆调整的递归运算。

【源程序代码】

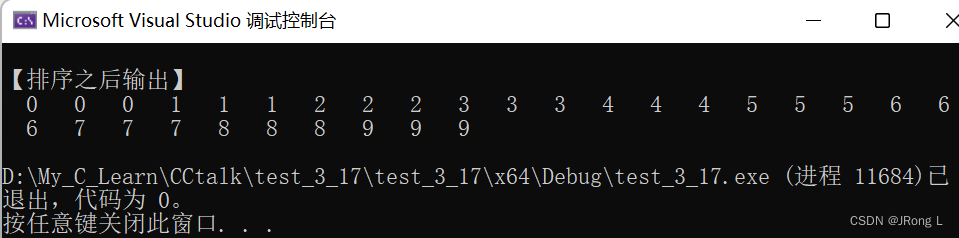
#include <stdio.h>
#include <stdlib.h>

void swap(int* a, int* b)
{
    int temp = *b;
    *b = *a;
    *a = temp;
}

void max_heapify(int arr[], int start, int end)
{
    //建立父节点指标和子节点指标
    int dad = start;
    int son = dad * 2 + 1;
    while (son <= end)  //若子节点指标在范围内才做比较
    {
        if (son + 1 <= end && arr[son] < arr[son + 1])
            //先比较两个子节点大小，选择最大的
            son++;
        if (arr[dad] > arr[son]) //如果父节点大於子节点代表调整完毕，直接跳出函数
            return;
        else  //否则交换父子内容再继续子节点和孙节点比较
        {
            swap(&arr[dad], &arr[son]);
            dad = son;
            son = dad * 2 + 1;
        }
    }
}

void heap_sort(int arr[], int len)
{
    int i;
    //初始化，i从最後一个父节点开始调整
    for (i = len / 2 - 1; i >= 0; i--)
        max_heapify(arr, i, len - 1);
    //先将第一个元素和已排好元素前一位做交换，再重新调整，直到排序完毕
    for (i = len - 1; i > 0; i--)
    {
        swap(&arr[0], &arr[i]);
        max_heapify(arr, 0, i - 1);
    }
}

int main() {
    int arr[] = { 3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6 };
    int len = (int)sizeof(arr) / sizeof(*arr);
    heap_sort(arr, len);
    int i;

    printf("\n【排序之后输出】\n");
    for (i = 0; i < len; i++)
        printf("%3d ", arr[i]);
    printf("\n");
    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57

【运行结果】
在这里插入图片描述

八、【计数排序算法】

计数排序是一个非基于比较的排序算法，该算法于1954年由 Harold H. Seward 提出。它的优势在于在对一定范围内的整数排序时，它的复杂度为Ο(n+k)（其中k是整数的范围），快于任何比较排序算法。当然这是一种牺牲空间换取时间的做法，而且当O(k)>O(nlog(n))的时候其效率反而不如基于比较的排序（基于比较的排序的时间复杂度在理论上的下限是O(nlog(n)), 如归并排序，堆排序）

在这里插入图片描述

【算法思想】
计数排序对输入的数据有附加的限制条件：
1、输入的线性表的元素属于有限偏序集S；
2、设输入的线性表的长度为n，|S|=k（表示集合S中元素的总数目为k），则k=O(n)。
在这两个条件下，计数排序的复杂性为O(n)。
计数排序的基本思想是对于给定的输入序列中的每一个元素x，确定该序列中值小于x的元素的个数（此处并非比较各元素的大小，而是通过对元素值的计数和计数值的累加来确定）。一旦有了这个信息，就可以将x直接存放到最终的输出序列的正确位置上。例如，如果输入序列中只有17个元素的值小于x的值，则x可以直接存放在输出序列的第18个位置上。当然，如果有多个元素具有相同的值时，我们不能将这些元素放在输出序列的同一个位置上，因此，上述方案还要作适当的修改。

【源程序代码】

#include <stdio.h>
#include <stdlib.h>
#define random(x) rand()%(x)
#define NUM 100     // 产生100个随机数
#define MAXNUM 200     //待排序的数字范围是0-200
void countingSort(int A[], int n, int k) {
    int* c, * b;
    int i;
    c = (int*)malloc(sizeof(int) * k);/*临时数组,注意它的大小是待排序序列中值最大的那个。如假定该排序序列中最大值为1000000，则该数组需要1000000*sizeof(int)个存储单元*/
    b = (int*)malloc(sizeof(int) * n);  /*存放排序结果的数组*/
    for (i = 0; i < k; i++)
        c[i] = 0;                       /*初始化*/
    for (i = 0; i < n; i++)
        c[A[i]] += 1;                   /*统计数组A中每个值为i的元素出现的次数*/
    for (i = 1; i < k; i++)
        c[i] = c[i - 1] + c[i];         /*确定值为i的元素在数组c中出现的位置*/
    for (i = n - 1; i >= 0; i--)
    {
        b[c[A[i]] - 1] = A[i];       /*对A数组，从后向前确定每个元素所在的最终位置;*/
        c[A[i]] -= 1;
    }
    for (i = 0; i < n; i++)
        A[i] = b[i];                /*这个目的是返回A数组作为有序序列*/
    free(c);
    free(b);
}
void printArray(int A[], int n) {
    int i = 0;
    for (i = 0; i < n; i++) {
        printf("%4d", A[i]);
    }
    printf("\n");
}
/*测试*/
int main()
{
    int A[NUM];
    int i;
    for (i = 0; i < NUM; i++)
        A[i] = random(MAXNUM);
    printf("\n\nBefore sorting:\n");
    printArray(A, NUM);
    countingSort(A, NUM, MAXNUM);
    printf("\n\nAfter sorting:\n");
    printArray(A, NUM);
    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47

【运行结果】
在这里插入图片描述

九、【计数排序算法】

桶排序 (Bucket sort)或所谓的箱排序，是一个排序算法，工作的原理是将数组分到有限数量的桶子里。每个桶子再个别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序）。桶排序是鸽巢排序的一种归纳结果。当要被排序的数组内的数值是均匀分配的时候，桶排序使用线性时间（Θ（n））。但桶排序并不是 比较排序，他不受到 O(n log n)下限的影响。

在这里插入图片描述
【源程序代码】

#include <stdio.h>
#include <stdlib.h>

typedef struct node {
	int key;
	struct node* next;
}KeyNode;

void bucket_sort(int keys[], int size, int bucket_size) {
	int i, j;
	KeyNode** bucket_table = (KeyNode**)malloc(bucket_size * sizeof(KeyNode*));
	for (i = 0; i < bucket_size; i++) {
		bucket_table[i] = (KeyNode*)malloc(sizeof(KeyNode));
		bucket_table[i]->key = 0;
		bucket_table[i]->next = NULL;
	}
	for (j = 0; j < size; j++) {
		KeyNode* node = (KeyNode*)malloc(sizeof(KeyNode));
		node->key = keys[j];
		node->next = NULL;
		int index = keys[j] / 10;
		KeyNode* p = bucket_table[index];
		if (p->key == 0) {
			bucket_table[index]->next = node;
			(bucket_table[index]->key)++;
		}
		else {
			while (p->next != NULL && p->next->key <= node->key)
				p = p->next;
			node->next = p->next;
			p->next = node;
			(bucket_table[index]->key)++;
		}
	}
	//print result
	KeyNode* k = NULL;
	for (i = 0; i < bucket_size; i++)
		for (k = bucket_table[i]->next; k != NULL; k = k->next)
			printf("%d ", k->key);
	printf("\n");
}


int main()
{
	int raw[] = { 49,38,65,97,76,13,27,49 };
	int size = sizeof(raw) / sizeof(int);
	printf("\n\n【排序后输出结果为】\n\n");
	bucket_sort(raw, size, 10);

	return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52

【运行结果】
在这里插入图片描述

十、【计数排序算法】

基数排序（radix sort）属于“分配式排序”（distribution sort），又称“桶子法”（bucket sort）或bin sort，顾名思义，它是透过键值的部份资讯，将要排序的元素分配至某些“桶”中，藉以达到排序的作用，基数排序法是属于稳定性的排序，其时间复杂度为O (nlog(r)m)，其中r为所采取的基数，而m为堆数，在某些时候，基数排序法的效率高于其它的稳定性排序法。

在这里插入图片描述
【源程序代码】

#include <stdio.h>
#include <string.h>

/* 获取输入数字的索引值，dec指定数字的位数，3代表百位数，order指定需要获取哪一位的索引，1代表个位，2代表十位，3代表百位 */
int get_index(int num, int dec, int order)
{
    int i, j, n;
    int index;
    int div;

    /* 根据位数，循环减去不需要的高位数字 */
    for (i = dec; i > order; i--) {
        n = 1;
        for (j = 0; j < dec - 1; j++)
            n *= 10;
        div = num / n;
        num -= div * n;
        dec--;
    }

    /* 获得对应位数的整数 */
    n = 1;
    for (i = 0; i < order - 1; i++)
        n *= 10;

    /* 获取index */
    index = num / n;

    return index;
}

/* 进行基数排序 */
void radix_sort(int array[], int len, int dec, int order)
{
    int i, j;
    int index;     /* 排序索引 */
    int tmp[30];  /* 临时数组，用来保存待排序的中间结果 */
    int num[10];   /* 保存索引值的数组 */
    memset(num, 0, 10 * sizeof(int));  /* 数组初始清零 */
    memset(tmp, 0, len * sizeof(int)); /* 数组初始清零 */

    if (dec < order) /* 最高位排序完成后返回 */
        return;

    for (i = 0; i < len; i++) {
        index = get_index(array[i], dec, order);  /* 获取索引值 */
        num[index]++;  /* 对应位加一 */
    }

    for (i = 1; i < 10; i++)
        num[i] += num[i - 1]; /* 调整索引数组 */

    for (i = len - 1; i >= 0; i--) {
        index = get_index(array[i], dec, order);  /* 从数组尾开始依次获得各个数字的索引 */
        j = --num[index];  /* 根据索引计算该数字在按位排序之后在数组中的位置 */
        tmp[j] = array[i]; /* 数字放入临时数组 */
    }

    for (i = 0; i < len; i++)
        array[i] = tmp[i];  /* 从临时数组复制到原数组 */

    printf("the %d time\n", order);
    for (i = 0; i < 30; i++)
        printf("%d  ", array[i]);
    printf("\n");

    /* 继续按高一位的数字大小进行排序 */
    radix_sort(array, len, dec, order + 1);

    return;
}

int main(int argc, char* argv[])
{
    int i;
    int array[30] = { 258, 976, 515, 337, 359, 701, 916, 494, 303, 175,
                        677, 825, 131, 560, 147, 254, 759, 814, 917, 382,
                        452, 114, 873, 585, 881, 127, 819, 658, 461, 435 };

    int len = 30;  /* 测试数据个数 */
    int dec = 3;   /* 数据位数，3代表3位数 */
    int order = 1; /* 排序的位数，1代表个位、2代表十位、3代表百位 */

    printf("before\n");
    for (i = 0; i < 30; i++)
        printf("%d  ", array[i]);
    printf("\n");

    /* 排序函数，从个位开始 */
    radix_sort(array, len, dec, order);

    printf("final\n");
    for (i = 0; i < 30; i++)
        printf("%d  ", array[i]);
    printf("\n");

    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90
  • 91
  • 92
  • 93
  • 94
  • 95
  • 96
  • 97
  • 98

【运行结果】
在这里插入图片描述

写在最后

本小白的此次分享就到这里结束啦，欢迎各位佬多多指正

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/很楠不爱3/article/detail/278011
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号