生成模型（自编码器、VAE、GAN）_latent representation

来自Manolis Kellis教授（MIT计算生物学主任）的课《人工智能与机器学习》，中间结合李沐的一个精读视频（GAN）作为补充

主要内容就是生成模型，包括自编码器（Autoencoder）、变分自编码器（VAE）和生成对抗网络（GAN）

由于这部分在我学习的课程中不到15分钟，所以内容很少，下面贴出油管链接（这个有一个半小时）：

Kellis教授详细的课：Generative Models, Adversarial Networks GANs, Variational Autoencoders VAEs, Representation Learning

生成模型，最经典和热门的就是VAE（变分自编码器）和GAN（生成对抗网络）。

一篇不错的博客：【ML】 第17章 使用自动编码器和 GAN 的表示学习和生成学习

生成模型（Generative Models）和传统的深度学习神经网络是机器学习中两种不同的建模方法，它们的主要区别主要体现在如何学习数据以及预测未来的方式上。

1. 生成模型（Generative Models）：生成模型的目标是学习数据的真实分布，以便能生成新的数据。这些模型会尝试捕获数据的内在结构或者模式，然后用来生成新的、相似的数据。这意味着生成模型可以生成新的、从未见过的数据实例。典型的生成模型包括生成对抗网络（GANs）、变分自编码器（VAEs）和自回归模型等。

   重点：生成模型关注的是学习和理解输入数据的整体分布，并尝试从这个分布中生成新的数据实例。

2. 传统的深度学习神经网络：这类神经网络主要通过学习输入与输出之间的映射关系进行预测。这种方法通常用于监督学习任务，如分类或回归问题。例如，对于一个图片分类任务，神经网络会尝试学习从图片（输入）到类别标签（输出）的映射关系。典型的这类模型包括卷积神经网络（CNNs）、循环神经网络（RNNs）、全连接网络（DNNs）等。

   重点：传统的深度学习神经网络主要关注学习输入到输出的映射关系，并根据学习到的映射关系进行预测。

总的来说，生成模型和传统的深度学习神经网络的最大区别在于它们的目标不同：生成模型试图理解和生成与训练数据相似的新数据，而传统的深度学习神经网络则试图理解输入数据与输出数据间的映射关系。

自编码器

自编码器就是试图使其输出等于输入的模型。

先放两个快速入门视频，加起来就十分钟

让机器学习重画图（自动编码器Autoencoder）

61 编码器-解码器架构【动手学深度学习v2】

Autoencoder

首先还是得说明一下为什么要有自编码器。我们根据猫猫的图片，要最后生成猫猫的图片，达到最后以假乱真的效果，这个过程不是简单的输入复制到输出。根据自编码器的结构，我们中间是必然有个数据压缩的过程，这个过程可以保证不是简单的复制，而是学到了重要的东西。

• 自编码器是一种特殊的神经网络，它的输入和输出是相同的。它由两部分组成：编码器（Encoder）和解码器（Decoder）。

  • 编码器将高维的输入数据压缩成低维的表征（通常称为“瓶颈”或"bottleneck"）
  • 解码器将这个低维表征恢复成高维的数据。编码器和解码器通常都是神经网络。

• 训练自编码器的过程就是让自编码器学习一个函数，这个函数可以将输入数据编码和解码，使得解码后的数据尽可能接近原始的输入数据。由于自编码器在编码过程中会将数据压缩到低维，所以它常常被用于数据的降维。

• 自编码器的另一个应用是特征学习。自编码器在编码过程中会学习到输入数据的有效表示，这些表示可以捕捉到输入数据的关键特征。在许多应用中，这些特征比原始的输入数据更有用。（编码的过程就是特征抽取，类似CNN的卷积层）

• 使用**限制性玻尔兹曼机（RBM）**进行预训练的方法。这是一个常见的策略，用来帮助自编码器学习更好的表征。具体来说，我们可以先用RBM在无标签的数据上进行预训练，然后将RBM的输出作为自编码器的输入进行训练。这种预训练的方法可以帮助自编码器学习到更好的特征表示。

• 使用反向传播（Backpropagation）进行微调的步骤。这是指在预训练之后，我们会使用反向传播算法对自编码器进行微调，使得它的输出更接近输入数据。这个步骤也被称为“微调”或"fine-tuning"。

潜在表示（latent representation）

编码器的输出就是潜在表示（latent representation）

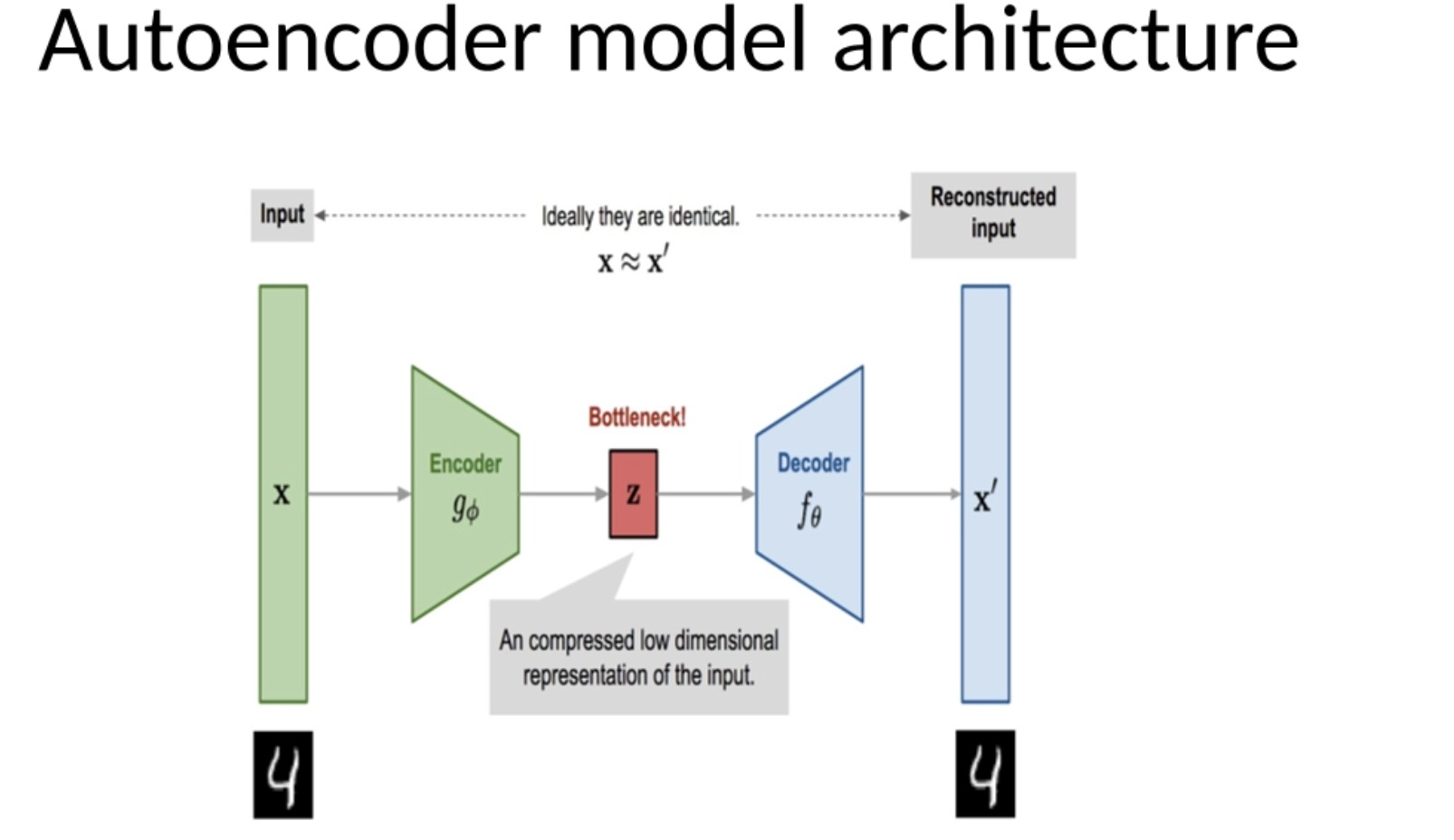
自编码器是一种神经网络模型，它的目标是找到输入数据的潜在表示（latent representation），并通过这个表示重构输入数据。它由编码器和解码器两部分组成，编码器将输入数据压缩到一个潜在空间，而解码器则试图从这个潜在空间恢复原始的输入数据。

然而，传统的自编码器存在一些缺点（在那个科普视频里提到，比较形象）：

1. 没有对潜在表示的约束：这意味着在潜在空间中可能存在“空洞”或“间隙”（gaps），即某些区域可能没有对应的有效输入。这使得从潜在空间中随机抽样并通过解码器生成新的样本变得困难。
2. 易于过拟合：自编码器可能会“记住”输入数据，而不是学习到数据的真实结构或分布。特别是当模型的复杂度（如神经元数量或层数）过高时，自编码器可能会几乎复制输入数据，而不是找到其潜在表示。
3. 不清楚如何生成新的样本：由于上述问题，传统的自编码器并不能直接用于生成新的数据。虽然它们可以重构输入数据，但在潜在空间中生成有意义的新数据通常是困难的。

• 自编码器的结构如图

VAE

补充学习视频：17-机器视觉-13 生成模型VAE

为了解决这些问题，研究人员提出了多种变体，例如变分自编码器（Variational Autoencoder，VAE）。VAE通过引入随机性和对潜在空间的显式约束（例如假设潜在变量遵循某种已知的概率分布，如高斯分布），使得模型可以更好地学习数据的潜在结构，并能够生成新的样本。

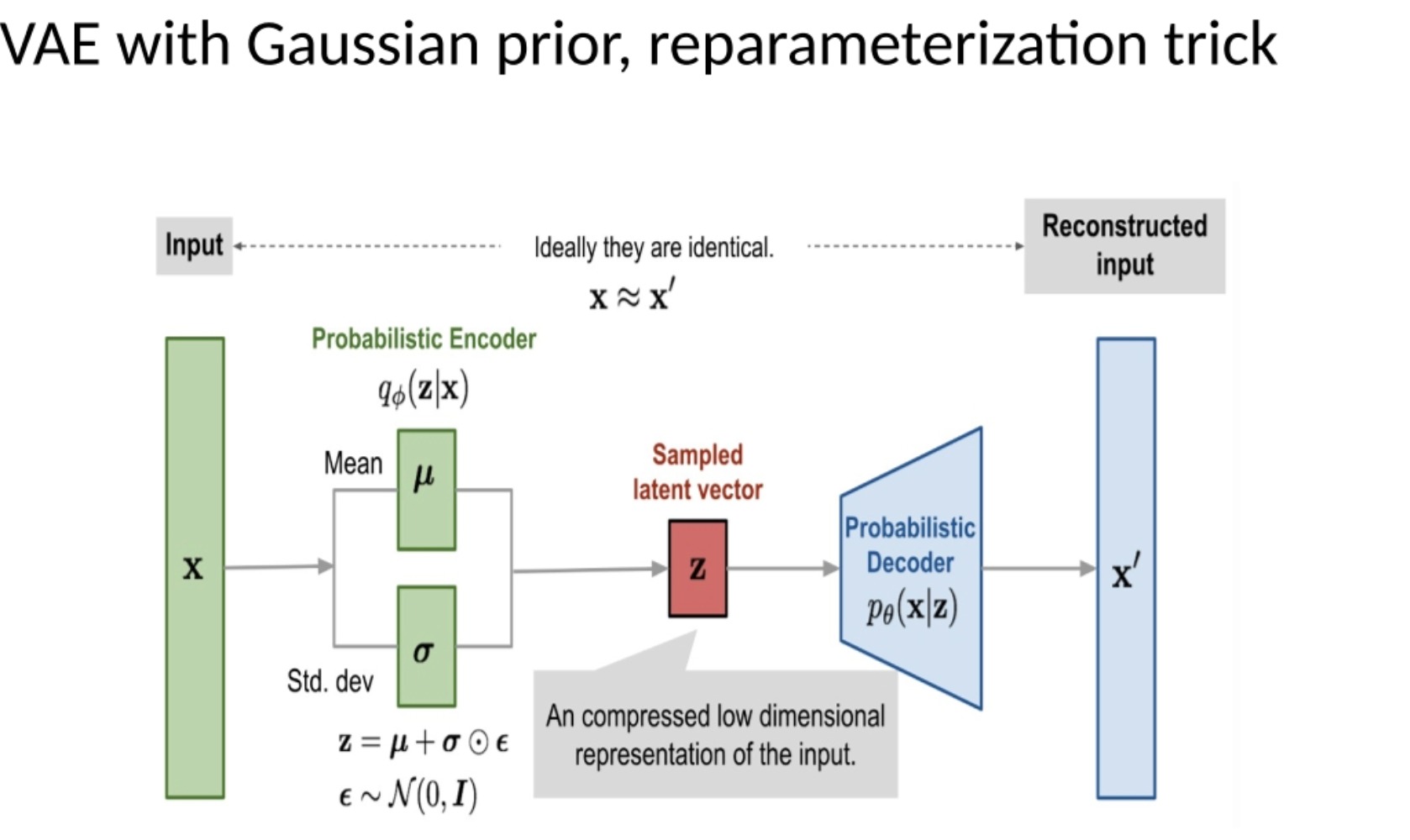
• VAE的结构

• VAE的结构包括一个概率编码器和一个概率解码器。概率编码器将输入数据编码成一个潜在向量，但不同于传统的自编码器，这个潜在向量不是一个固定的值，而是一个概率分布的参数（例如高斯分布的均值和标准差）。然后，我们从这个分布中采样一个潜在向量，将其输入到概率解码器中，生成重构的输入数据。

• VAE的一个关键技巧是"重参数化技巧"（reparameterization trick）。这个技巧允许我们在训练过程中通过反向传播优化概率编码器和概率解码器。具体来说，我们将潜在向量的采样过程写成一个确定性的函数和一个独立的噪声项的和。例如，如果我们假设潜在向量遵循高斯分布，那么我们可以将潜在向量表示为均值加上标准差乘以一个标准正态分布的随机噪声。这样，我们就可以将所有的随机性归因于噪声项，而将确定性的函数（即编码器和解码器）通过反向传播进行优化。

• “ideally they are identical”，这可能是指VAE的目标是使重构的输入数据尽可能接近原始的输入数据。这一目标通过最小化重构损失和一个正则化项（通常是KL散度）来实现，KL散度项鼓励潜在空间的分布接近先验分布（例如标准正态分布）。

• “An compressed low dimensional representation of the input”，这是指VAE的潜在向量，它是输入数据的低维压缩表示，捕捉了输入数据的关键信息。通过调整这个潜在向量，我们可以生成新的数据样本，这是VAE的一个主要优点。

迁移学习

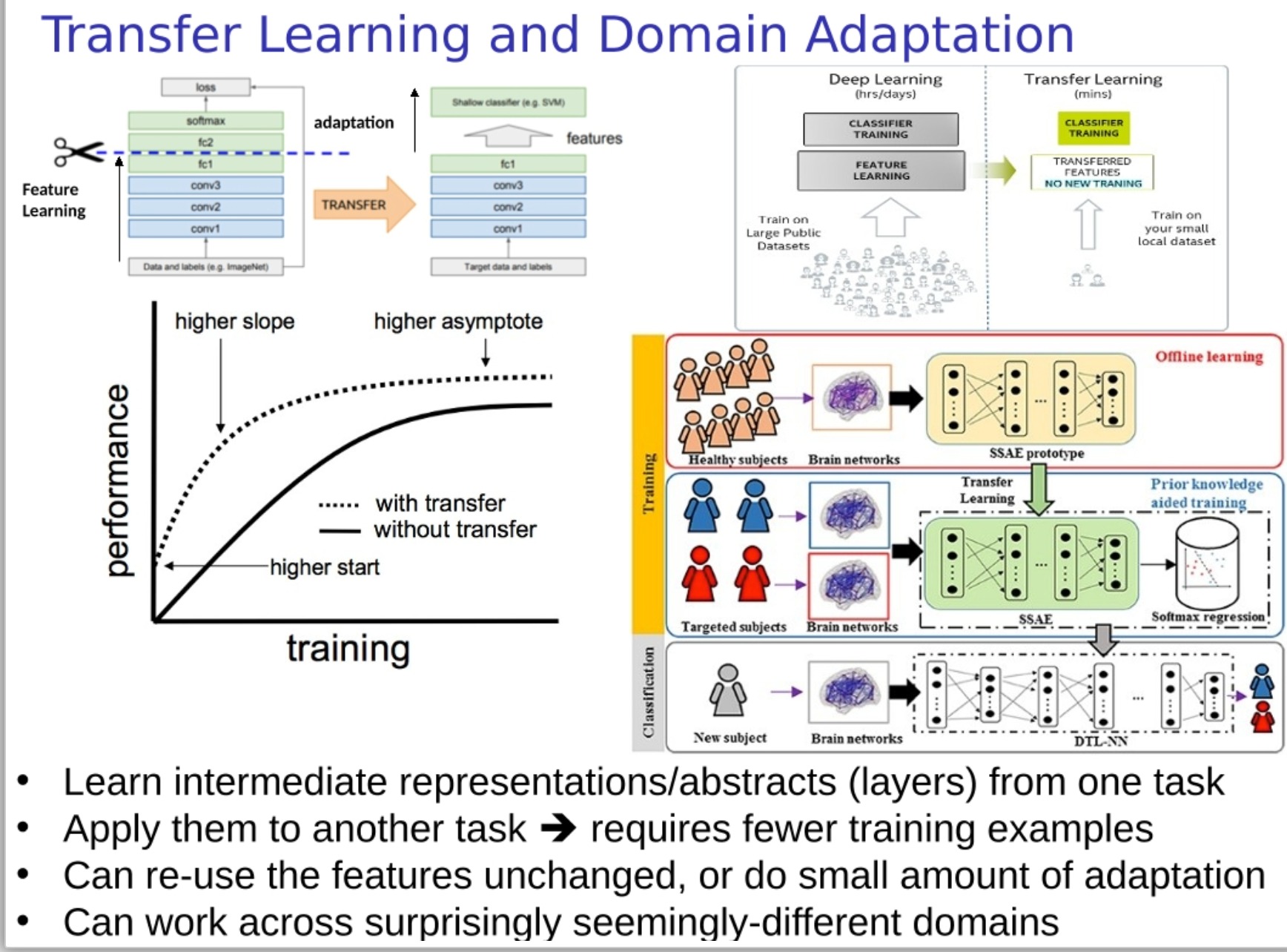
迁移学习：迁移学习是一种机器学习策略，它利用在源任务上学习到的知识来帮助解决目标任务。例如，如果我们已经在一个大型公共数据集（如ImageNet）上训练了一个深度神经网络，那么我们可以利用这个网络在目标任务（如医疗影像识别）上的表现。这通常会在目标任务的数据集较小时带来显著的性能提升。

具体来说，我们通常会将源任务的模型的卷积层（conv layers）作为特征提取器使用，并在其上加一个新的全连接层（fc layer）和softmax层进行分类。全连接层和softmax层会在目标任务的数据上进行训练，而卷积层可以选择冻结（不训练）或进行微调。

领域适应：领域适应是迁移学习的一个特例，它主要关注的是源任务和目标任务的数据分布不一致的情况。例如，我们可能在清晰的照片上训练了一个人脸识别模型，但我们希望在模糊的监控视频中使用这个模型。在这种情况下，我们需要进行领域适应，以使模型能够适应目标领域的数据分布。

领域适应通常涉及到一些特殊的技术，如领域对抗神经网络（Domain-Adversarial Neural Network, DANN）。DANN通过对模型添加一个领域分类器，使模型在源领域和目标领域的数据上的表现尽可能一致，从而达到领域适应的目标。

总的来说，迁移学习和领域适应都是利用源任务的知识来帮助解决目标任务，它们在许多实际应用中都表现出了显著的效果

生成对抗网络GAN

李沐论文精读

沐神：GAN论文逐段精读【论文精读】

论文：https://arxiv.org/pdf/1406.2661.pdf【最早版本的】

Generative Adversarial Nets

摘要

我们提出了一种新的框架，通过对抗过程来估计生成模型，该过程中我们同时训练两个模型：一个是生成模型G，捕获数据分布；另一个是判别模型D，估计一个样本来自训练数据的概率，而非从模型G生成。模型G的训练过程是最大化模型D出错的概率。这个框架对应一个极小极大两人博弈。在任意函数G和D的空间中，存在一个唯一的解决方案，模型G能恢复训练数据分布，模型D在各处等于0。在模型G和D被定义为多层感知机的情况下，整个系统可以通过反向传播进行训练。在训练或生成样本过程中，无需任何马尔可夫链或展开近似推断网络。实验证明，通过定性和定量评估生成的样本，该框架具有巨大潜力。

导言

作者认为深度学习不仅仅是神经网络，更多的是对整个数据分布的一个特征的表示。目前DL在辨别模型上表现还可以，但在生成模型上表现很差。原因是在最大化似然函数的时候，要对概率分布进行很多近似，这个近似带来了很多计算上的困难。意思就是说我不用去近似你那个似然函数了，我有其他方法得到一个好的计算模型（其实还是近似似然函数 只是KL divergence这个度量本身也拿来近似了。）。

在我们提出的对抗网络框架中，生成模型与一个对手即判别模型对立：判别模型学习判断一个样本是来自模型分布还是数据分布。生成模型可以被视为类似于造假币的团队，试图制造假币并在不被检测的情况下使用，而判别模型可以被视为警察，试图检测出假币。这个游戏中的竞争驱使两个团队都提升他们的方法，直到假币与真币无法区分。

这个框架可以产生针对许多类型的模型和优化算法的特定训练算法。**在这篇文章中，我们探索了生成模型通过多层感知器传递随机噪声生成样本，而判别模型也是多层感知器的特殊情况。我们称这个特殊情况为对抗网络。**在这种情况下，我们可以使用高度成功的反向传播和dropout算法来训练两种模型，并且仅使用前向传播从生成模型中采样。不需要近似推断或马尔可夫链(复杂的采样)。

首先搞明白噪声的定义是均匀分布的数据 MLP是拟合数据分布特征 所以才会输入噪音的说法

输入噪声是为了提供随机性。在生成模型中，特别是在对抗生成网络(GAN)中，我们希望模型能生成多样性的样本，而不仅仅是重复或复制训练数据。这种多样性的一种来源就是输入噪声。噪声提供了随机性，使得每次通过模型生成的样本都有所不同。

将噪声作为输入，能使模型学习将这个噪声映射到数据的分布上。模型不断调整自己的参数，以尽量使噪声经过模型处理后生成的样本更接近真实数据的分布。这是一个动态的过程，模型会不断地通过学习来改善这种映射，使得生成的样本能更好地反映真实数据的特性。

此外，通过输入噪声，可以拟合数据的分布特征，这是因为这个过程实际上是在模拟数据生成的过程。在现实世界中，数据的生成往往也是伴随着各种不确定性和随机性的，这些随机性就像是噪声一样。因此，我们通过将噪声输入到模型中，实际上是在模拟这种数据生成的过程，使得生成的样本能更好地反映数据的分布特性。

• 举个例子

我们可以想象一下生成模型就像一个画家，而噪声就像他的灵感来源。

画家需要画一张和给定样本（比如说一幅著名的油画）相似的画。画家每次画画的时候，都会受到一些随机的灵感（这就是噪声）。这些灵感会影响他的画作，使得每一次他画出来的画都有一些细微的不同。然而，尽管他的每一幅画都不完全相同，但是他的目标是让他的画作尽可能地接近那幅著名的油画。

开始的时候，画家可能还不是很擅长画画，他的画和著名的油画相去甚远。但是，通过不断地练习和改进，他的技巧会越来越好，他的画作也会越来越接近那幅著名的油画。最终，他可能会达到一个点，他的画作已经无法被人类观察者区分出是否为原作。

这就是生成模型（画家）如何通过输入噪声（灵感）来拟合数据（著名的油画）的分布特征。噪声提供了一种随机性，使得模型生成的样本具有多样性，同时模型通过学习和优化，使得这些生成的样本尽可能地接近真实的数据分布。

相关工作

直到近期，大部分关于深度生成模型的研究都集中在提供概率分布函数参数化规定的模型上。然后，这种模型可以通过最大化对数似然来进行训练。在这个模型系列中，可能最成功的就是深度Boltzmann机器。这种模型通常有难以处理的似然函数，因此需要对似然梯度进行大量近似。这些困难激发了“生成机器”的开发——这些模型并不明确表示似然，但却能从期望的分布中生成样本。生成随机网络就是一种可以通过精确的反向传播进行训练的生成机器，而不是像Boltzmann机器那样需要大量的近似。我们的工作扩展了生成机器的理念，通过使用观察到的结果进行反向传播梯度，消除了生成随机网络中使用的马尔可夫链。

以往的深度生成模型，如深度Boltzmann机器，往往需要对复杂的似然函数进行近似处理，这导致了训练过程的困难。为了解决这个问题，研究者发展出了不直接依赖似然的生成模型，例如生成随机网络，这些模型能更简单地通过反向传播进行训练。本文的工作进一步扩展了这种生成模型的理念，消除了生成过程中的马尔可夫链，使得模型更简洁，训练过程更直接。

作者提及了他们在开发这项工作时并未意识到其他研究者已经开发了更为通用的随机反向传播规则，这些规则允许通过有限方差的高斯分布进行反向传播，并且可以向协方差参数以及均值进行反向传播。这种方法有可能使人们能够学习生成模型的条件方差，而在当前的工作中，这被视为超参数。

他们还提到了变分自编码器（VAEs）和生成对抗网络（GANs）的相似性和差异。两者都配备了一个可微分的生成网络和第二个神经网络，但是在VAEs中，第二个网络是执行近似推理的识别模型。相比之下，GANs则不能模拟离散数据，而VAEs不能具有离散的潜在变量。

此外，作者还讨论了一些其他的方法，例如噪声对比估计（NCE），它通过学习鉴别数据和噪声分布的权重来训练生成模型。然而，NCE的主要限制在于它的"鉴别器"需要能够评估和通过噪声分布和模型分布的概率密度进行反向传播。

最后，作者提到了他们的工作与“可预测性最小化”这个概念的不同之处。在可预测性最小化中，网络的每个隐藏单元都被训练成与第二个网络的输出不同，而在这项工作中，网络之间的竞争是唯一的训练标准，而且它本身就足以训练网络。

Adversarial net

视频从15:50到25:33

比较适合多听几遍(就懂了)，比笔记效果好

D目标是尽量完美，使得V最大；G目标是尽量使D犯错，使得V最小。并且我们最终要让G胜利，通过这种对抗中进步，能使得G的对手越来越厉害，相应的，G也会越来越厉害。

有点像EM算法

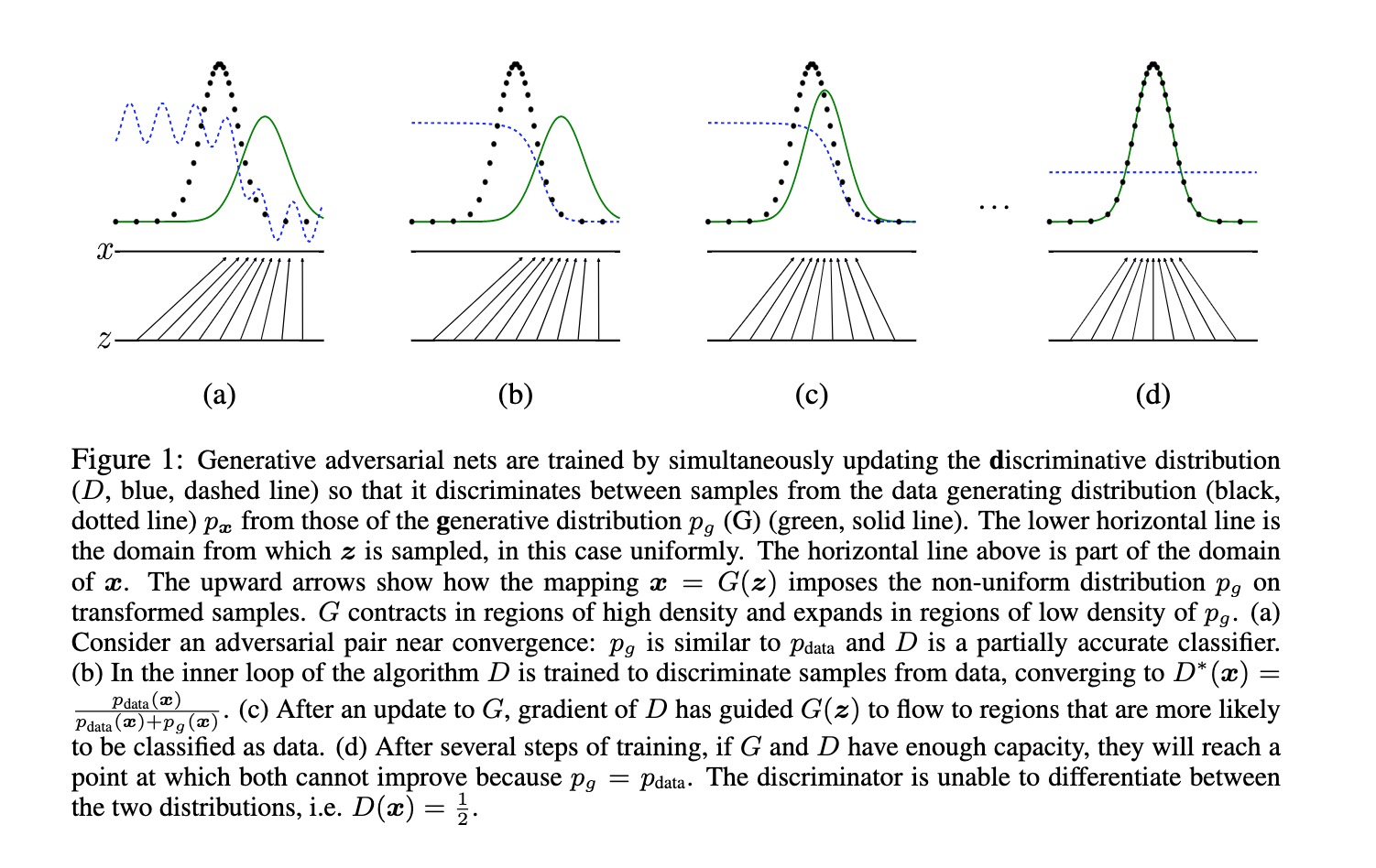
在对抗模型框架中，最直接的应用是在两个模型都是多层感知机（MLP）的情况下。为了学习生成器的数据分布pg，我们在输入噪声变量pe(z)上定义了一个先验，然后通过多层感知机将它映射到数据空间，得到G(z; θg)。同时，我们还定义了一个输出单一标量的多层感知机D(x; θd)，D(x)表示样本x来自真实数据的概率。我们同时训练D和G，使D最大化为训练样本和G生成的样本分配正确标签的概率，而G最小化log(1 - D(G(z)))。

在这个过程中，D和G实质上是在进行一种最小最大化的双人博弈，其目标函数为V(D, G)。理论分析表明，只要G和D给定足够的容量，这个训练标准就能恢复出数据生成的分布。

然而在实践中，需要通过迭代的数值方法来实现这个博弈。由于在有限数据集中完全优化D的计算成本过高，且会导致过拟合，所以我们选择在优化D的k步之后，优化G一步。这种策略类似于SML/PCD训练中的做法，即在学习的每一步都保持马尔科夫链的样本，以避免在学习的内层循环中进行马尔科夫链的燃烧。

此外，作者提到，在实践中，公式(1)可能并不提供足够的梯度以供G良好地学习。在学习初期，当G的性能较差时，D可以高度自信地拒绝样本，因为它们明显与训练数据不同。在这种情况下，log(1 - D(G(z)))会饱和。为了解决这个问题，我们可以训练G去最大化log D(G(z))，这样可以在学习初期提供更强的梯度。

所以，这段内容的核心点在于：

1. 描述了对抗模型框架的实施细节。
2. 提出了在训练中遇到的问题，以及针对这些问题的解决方案。
3. 指出在理论上，只要给定足够的模型容量，就能恢复出数据生成的分布。

后面的理论部分和证明真妙啊，光顾着听了，笔记以后在补充（挖坑+1）

简单总结

首先GAN是一个无监督学习，但是他用的是有监督学习的损失函数来训练。他数据的标号来自于数据（是采样的还是生成的），在训练上高效很多。这是以后自监督学习比如BERT的灵感来源。

精读挖坑（

还有一个精读笔记以后再补充（挖坑+2）：

同济子豪兄：生成对抗网络GAN开山之作论文精读

上课内容

Kellis教授这些讲的很快，就5张ppt，甚至还没讲（晕），就贴个图吧