算法导论-第15章-动态规划_算法导论 动态规划

动态规划（dynamic programming）的思想是分治思想和解决冗余。

• 与分治法相似的是
  • 将原问题分解为若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。
• 与分治法不同的是
  • 经分解的子问题往往不是相互独立的。若用分治法来解，有些共同部分（子问题或子子问题）被重复计算了很多次。
  • 而动态规划算法对每个子子问题只求解一次，将其解保存在一个表格中，从而无需每次求解一个子子问题时都需重新计算。

动态规划方法通常用来求解最优化问题（optimization problem）。这类问题可以有很多可行的解，每个解都有一个值，我们希望寻找具有最优值（最小值或最大值）的解。我们称这样的解为问题的一个最优解（an optimal solution），而不是最优解（the optimal solution），因为可能有多个解都是最优值。

我们通常按如下4步骤来设计一个动态规划算法：

1. 刻画一个最优解的结构特征。
2. 递归地定义最优解的值（写出动态规划方程）。
3. 计算最优解的值，通常采用自底向上的方法。
4. 利用计算出的信息构造一个最优解。

步骤1~3是动态规划求解问题的基础。如果我们仅仅需要最优解的一个值，而不是最优解本身，可以忽略步骤4。如果要构造最优解，则必须执行步骤4，步骤3中维护的一些额外信息是构造最优解的基础。

下面将讨论如何用动态规划求解最优解问题。15.1节将讨论如何将长钢条切割成短钢条，使其总价值最高。15.2节将讨论如何使用最少次数的标量乘法计算矩阵链乘。15.3节将讨论适合用动态规划求解的问题应该具备的两个关键特征。15.4节将讨论如何使用动态规划求解两个序列的最长公共子序列。15.5节用动态规划方法解决在已知关键字分布的前提下，如何构造最优二叉搜索树。

15.1 钢条切割

钢条切割问题：给定一段长度为 $n$ 英寸的钢条和一个价格表 $p_i(i=1,2,3,\cdots ,n)$。求切割钢条的方案，使得销售收益 $r_n$ 最大。注意，如果长度为 $n$ 英寸的钢条的价格 $p_n$ 足够大，最优解可能就是完全不需要切割。

假设Serling公司出售一段长度为 $i$ 英寸的钢条的价格为 $p_i$。钢条的长度均为整英寸，价格表如下：

考虑 $n=4$ 的情况。下图给出了4英寸钢条所有可能的切割方案，包括根本不切割的方案。最优解为方案c。

长度为 $n$ 的钢条有 $2^{n-1}$ 种不同的切割方案，因为在距离钢条左端 $i(i=1,2,\cdots ,n-1)$英寸处，都有切割或不切割两种选择。

如果一个最优解将钢条切割为 $k(1\le k\le n)$ 段，那么最优切割方案
$$n=i_1+i_2+\cdots +i_k$$
最大收益为
$$r_n=p_{i_1}+p_{i_2}+\cdots +p_{i_k}$$
一般地，对于$r_n(n\ge 1)$，可以用更短的钢条的最优切割收益来描述它：
$$r_n=max(p_n,r_1+r_{n-1},r_2+r_{n-2},\cdots ,r_{n-1}+r_1)$$
其中 $p_n$ 表示不切割，其他参数对应切割为长度为 $i$ 和 $n-i$ 的两段，接着求这两段短钢条的最优收益 $r_i$ 和 $r_{n-i}$。由于无法预知哪种划分方案会获得最大收益，需要遍历所有可能的 $i$，选取其中收益最大者。

15.4 最长公共子序列

[轻松掌握动态规划]5.最长公共子序列 LCS_哔哩哔哩_bilibili

子序列（subsequence）：给定一个序列 $X=<x_1,x_2,\cdots ,x_m>$，另一个序列 $Z=<z_1,z_2,\cdots ,z_k>$，存在一个严格递增的 $X$ 的下标序列 $<i_1,i_2,\cdots ,i_k>$，对所有 $j=1,2,\cdots ,k$，满足 $x_{i_j}=z_j$。例如，$Z=<B,C,D,B>$是 $X=<A,B,C,B,D,A,B>$的子序列，对应的下标序列为 $<2,3,5,7>$。

公共子序列（common subsequence）：给定两个序列 $X$ 和 $Y$，如果 $Z$ 既是 $X$ 的子序列，也是 $Y$ 的子序列，我们称它是 $X$ 和 $Y$ 的公共子序列。例如，$X=<A,B,C,B,D,A,B>$，$Y=<B,D,C,A,B,A>$，那么序列 $<B,C,A>$ 就是 $X$ 和 $Y$ 的公共子序列，但不是最长的公共子序列（LCS），因为它的长度为3；而 $<B,C,B,A>$ 也是 $X$ 和 $Y$ 的公共子序列，其长度为4。$<B,C,B,A>$ 是 $X$ 和 $Y$ 的最长公共子序列，$<B,D,A,B>$ 也是最长公共子序列，因为 $X$ 和 $Y$ 不存在长度大于等于5的公共子序列。

最长公共子序列问题（longest-common-subsequence problem）：给定两个序列 $X=<x_1,x_2,\cdots ,x_m>$ 和 $Y=<y_1,y_2,\cdots ,y_n>$，求 $X$ 和 $Y$ 的最长公共子序列。

步骤1：刻画最长公共子序列的特征

定理：LCS的最优子结构

令 $X=<x_1,x_2,\cdots ,x_m>$ 和 $Y=<y_1,y_2,\cdots ,y_n>$ 为两个序列， $Z=<z_1,z_2,\cdots ,z_k>$ 为 $X$ 和 $Y$ 的任意LCS。

1. 如果 $x_m=y_n$，则 $z_k=x_m=y_n$ 且 $Z_{k-1}$ 是 $X_{m-1}$ 和 $Y_{n-1}$ 的一个 LCS。
2. 如果 $x_m\ne y_n$ 且 $z_k\ne x_m$，那么 $Z$ 是 $X_{m-1}$ 和 $Y$ 的一个 LCS。
3. 如果 $x_m\ne y_n$ 且 $z_k\ne y_n$，那么 $Z$ 是 $X$ 和 $Y_{n-1}$ 的一个 LCS。

步骤2：一个递归解

根据LCS的最优子结构定理可知，在求 $X=<x_1,x_2,\cdots ,x_m>$ 和 $Y=<y_1,y_2,\cdots ,y_n>$ 的一个LCS时，我们需要求解一个或两个子问题。如果 $x_m=y_n$，我们应该求解 $X_{m-1}$ 和 $Y_{n-1}$ 的一个LCS，将 $x_m=y_n$ 追加到这个LCS的末尾，就得到 $X$ 和 $Y$ 的一个LCS。如果 $x_m\ne y_n$，我们必须求解两个子问题：求 $X_{m-1}$ 和 $Y$ 的一个 LCS 与 $X$ 和 $Y_{n-1}$ 的一个 LCS。两个LCS中较长者即为 $X$ 和 $Y$ 的一个LCS。

根据LCS的最优子结构性质，可得如下公式：
c [ i , j ] = { 0 若 i=0 或 j=0 c [ i − 1 , j − 1 ] + 1 若 i, j > 0 且  x i = y j m a x ( c [ i , j − 1 ] , c [ i − 1 , j ] ) 若 i, j > 0 且  x i ≠ y j c[i, j]=

$$\begin{cases} 0 &\text{若 i=0 或 j=0} \\ c[i-1,j-1]+1 &\text{若 i, j > 0 且 }x_i=y_j \\ max(c[i, j-1], c[i-1, j]) &\text{若 i, j > 0 且 }x_i \ne y_j\end{cases}$$ c[i,j]=⎩ ⎨ ⎧​0c[i−1,j−1]+1max(c[i,j−1],c[i−1,j])​若 i=0 或 j=0若 i, j > 0 且 xi​=yj​若 i, j > 0 且 xi​=yj​​

步骤3：计算LCS的长度

LCS问题有 $\Theta (mn)$ 个不同的子问题，可以采用自底向上动态规划进行计算。

LCS-LENGTH过程接受两个序列 $X=<x_1,x_2,\cdots ,x_m>$ 和 $Y=<y_1,y_2,\cdots ,y_n>$ 作为输入。将 $c[i,j]$ 的值保存在表 $c[\mathrm{0..}m,\mathrm{0..}n]$ 中，并按照行主次序（row-major order）计算表项（即首先从左到右计算 c 的第一行，然后计算第二行，以此类推）。过程中还维护了一个表 $b[\mathrm{1..}m,\mathrm{1..}n]$，帮助构造最优解。

LCS-LENGTH(X, Y, m, n)
    let b[1 : m, 1 : n] and c[0 : m, 0 : n] be new tables
    for i = 1 to m
        c[i, 0] = 0
    for j = 0 to n
        c[0, j] = 0
    for i = 1 to m   // compute table entries in row-major order
        for j = 1 to n
            if x_i == y_j
                c[i, j] = c[i - 1, j - 1] + 1
                b[i, j] = "↖"
            else if c[i - 1, j] ≥ c[i, j - 1]
                c[i, j] = c[i - 1, j]
                b[i, j] = "↑"
            else c[i, j] = c[i, j - 1]
                b[i, j] = "←"
    return c and b
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

下图显示了LCS-LENGTH对输入序列 $X=<A,B,C,B,D,A,B>$ 和 $Y=<B,D,C,A,B,A>$ 计算的结果。运行时间为 $\Theta (mn)$，因为每个表项的计算时间为 $\Theta (1)$。

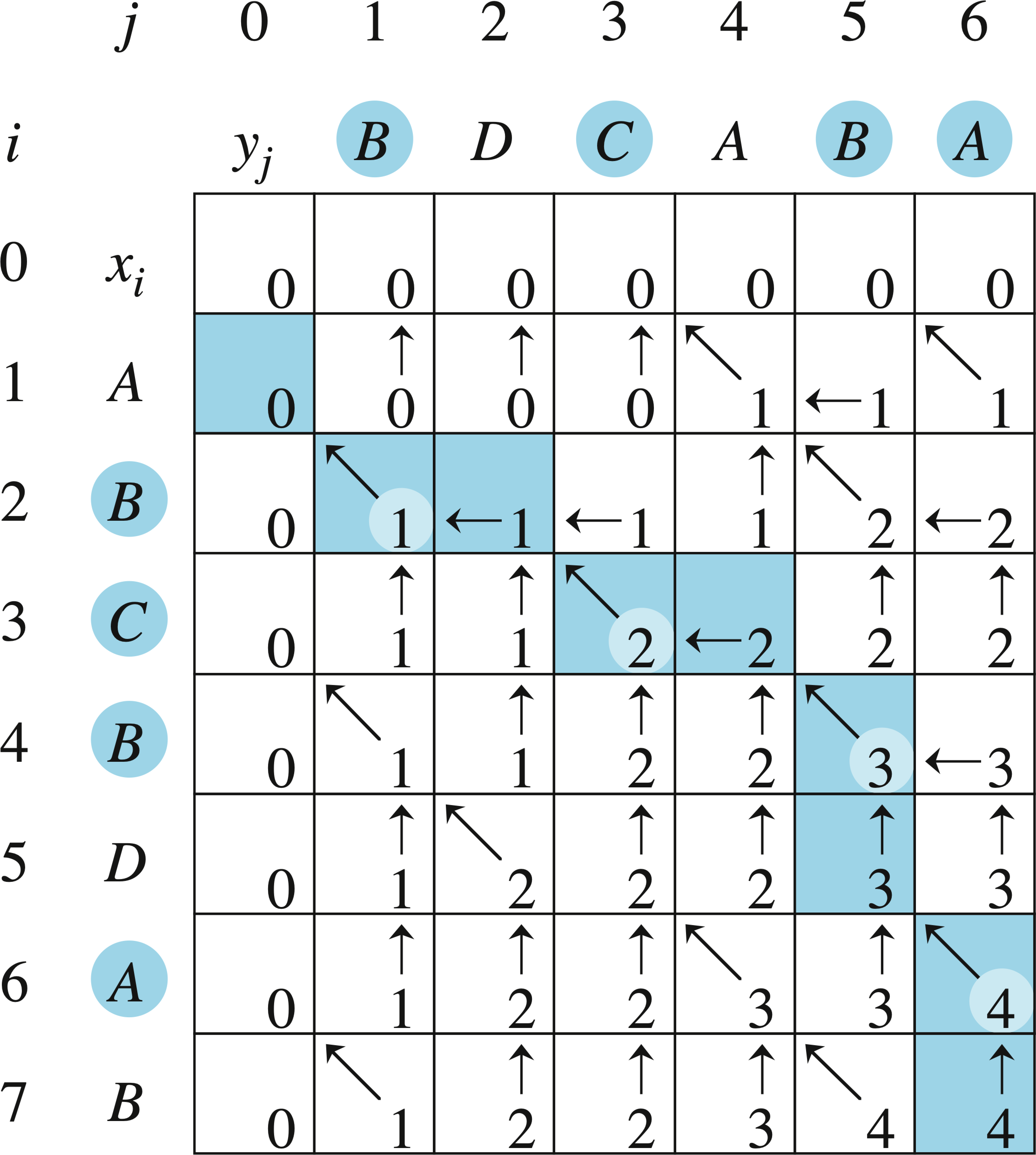
步骤4：构造LCS

要构造LCS，只需从 $b[m,n]$ 开始，按箭头追踪下去即可。当在表项中遇到”↖“时，意味着 $x_i=y_j$ 是LCS的一个元素。按照这种方法，就可以依次构造出LCS的所有元素。

PRINT-LCS(b, X, i, j)
    if i == 0 or j == 0
        return    // the LCS has length 0
    if b[i, j] == "↖"
        PRINT-LCS(b, X, i - 1, j - 1)
        print x_i    // same as y_i
    else if b[i, j] == "↑"
        PRINT-LCS(b, X, i - 1, j)
    else PRINT-LCS(b, X, i, j - 1)

PRINT-LCS(b, X, m, n)
1
2
3
4
5
6
7
8
9
10
11

也可以不依赖表 b。每个 $c[i,j]$ 项只依赖于表 c 中的其他三项：$c[i-1,j]、c[i,j-1]、c[i-1,j-1]$。这种方法节省了 $\Theta (mn)$ 的空间。此时的空间复杂度是 $\Theta (mn)$。

对空间复杂度进行优化

使用滚动数组对空间复杂度进行优化。

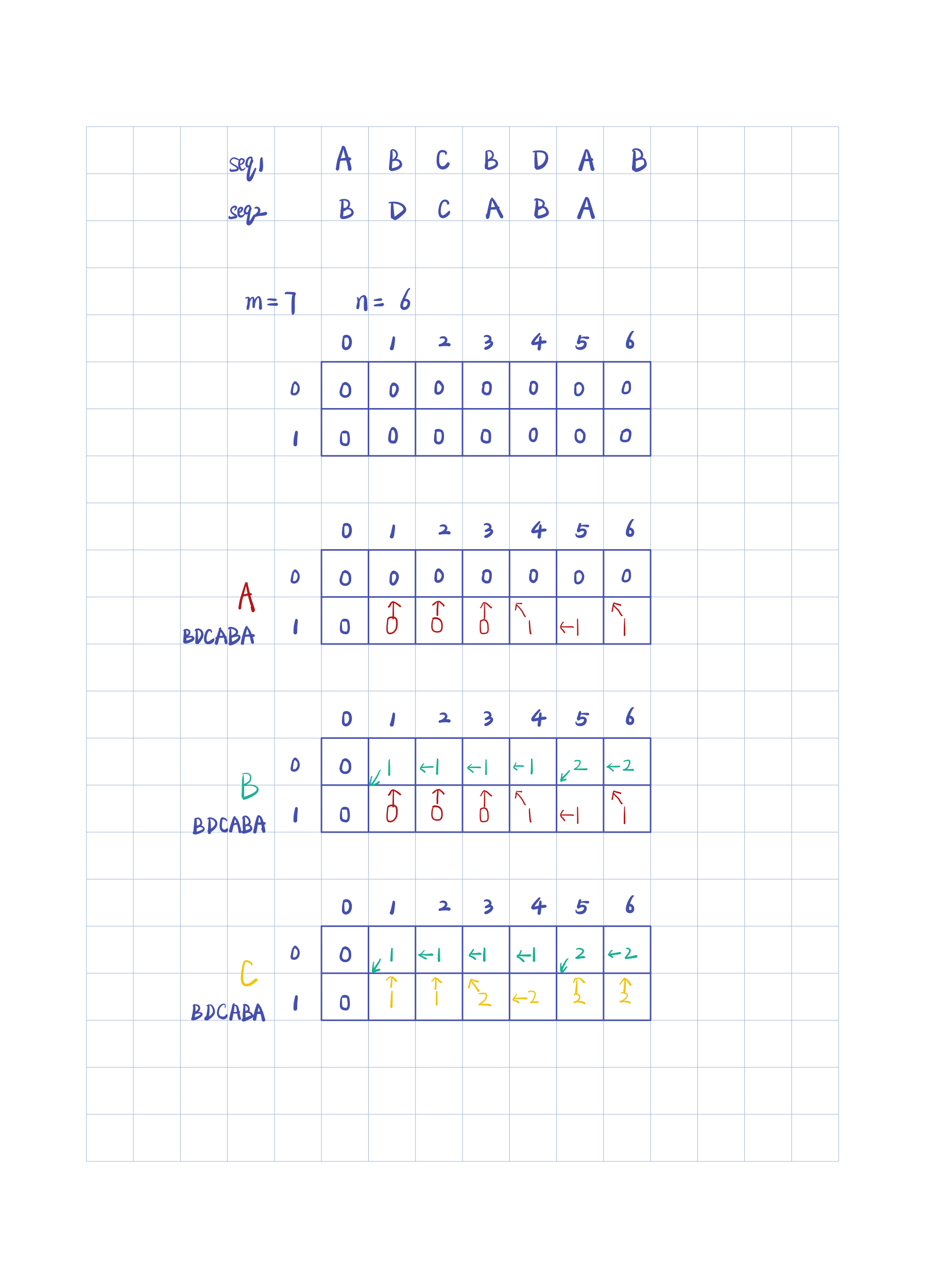
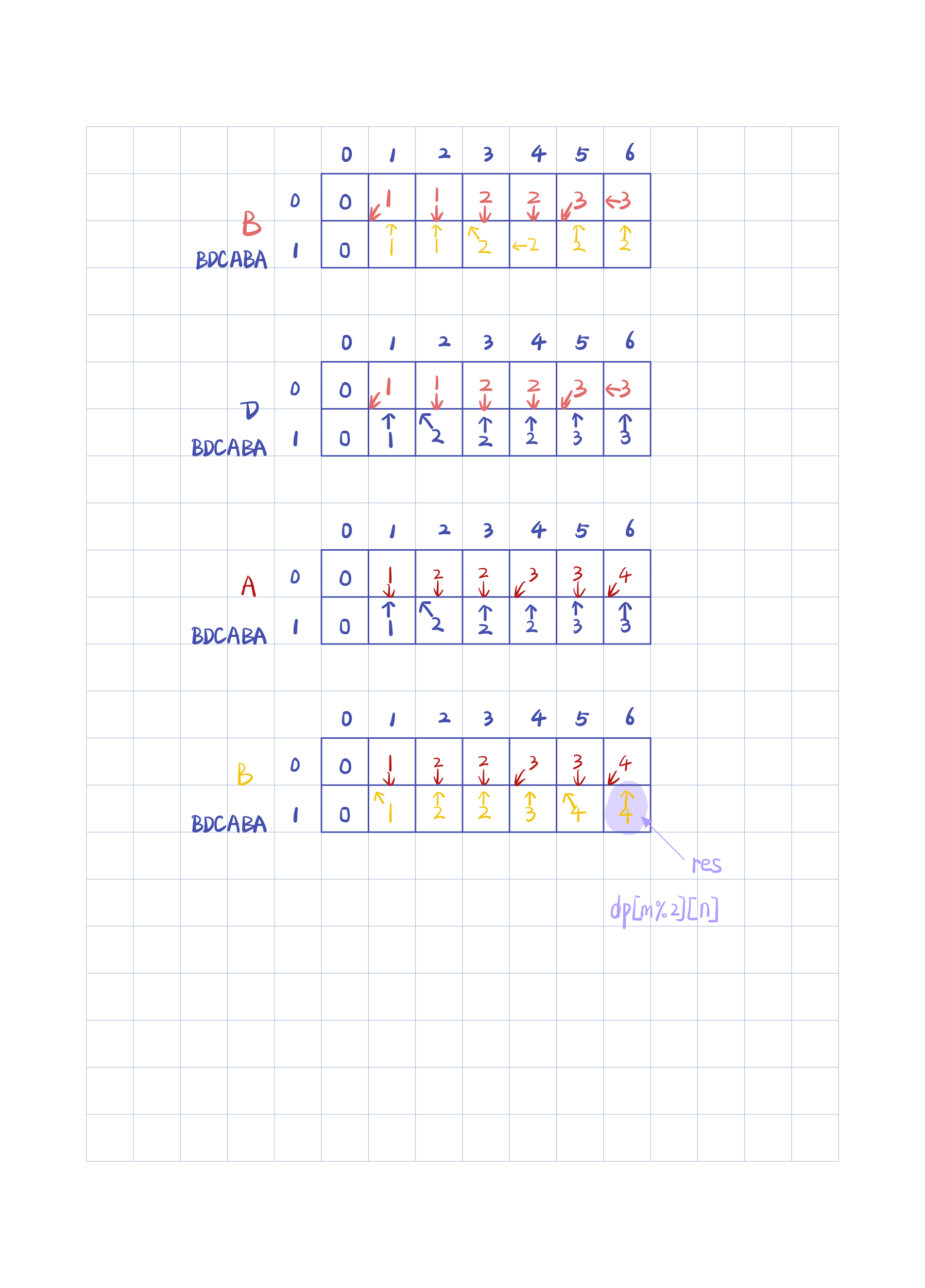
LCS的代码实现

编程实现最长公共子序列（LCS）算法，并理解其核心思想。

1. 时间复杂度$\mathrm{O}(mn)$，空间复杂度 $\mathrm{O}(mn)$，求出LCS及其长度。
2. 时间复杂度 $\mathrm{O}(mn)$，空间复杂度 $\mathrm{O}(2\ast min(m,n))$，求出LCS的长度。
3. 时间复杂度 $\mathrm{O}(mn)$，空间复杂度 $\mathrm{O}(min(m,n))$，求出LCS的长度。

输入：由控制台输入两个字符串text1，text2。

输出：控制台打印LCS的长度及相应的序列，如不存在公共子序列则返回0.

package ch15;

import java.util.Scanner;

public class LCS {
    /**
     * 最长公共子序列，空间复杂度O(mn)
     * @param seq1 序列1
     * @param seq2 序列2
     * @return LCS及其长度
     */
    public static String longestCommonSubsequence(String seq1, String seq2) {
        int m = seq1.length();
        int n = seq2.length();

        // 创建一个二维数组来保存子问题的解
        int[][] dp = new int[m + 1][n + 1];

        // 动态规划求解最长公共子序列
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (seq1.charAt(i - 1) == seq2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }

        // 从二维数组的右下角开始回溯，构造最长公共子序列
        StringBuilder lcs = new StringBuilder();
        int i = m, j = n;
        while (i > 0 && j > 0) {
            if (seq1.charAt(i - 1) == seq2.charAt(j - 1)) {
                lcs.insert(0, seq1.charAt(i - 1));
                i--;
                j--;
            } else if (dp[i - 1][j] > dp[i][j - 1]) {
                i--;
            } else {
                j--;
            }
        }
        return lcs.toString();
    }

    /**
     * 最长公共子序列，空间复杂度2 * O(min(m, n))
     * @param seq1 序列1
     * @param seq2 序列2
     * @return LCS长度
     */
    public static int longestCommonSubsequencesPro(String seq1, String seq2) {
        int m = seq1.length();
        int n = seq2.length();

        // 确保 n 是较小的值，以减小空间复杂度
        if (m < n) {
            String temp = seq1;
            seq1 = seq2;
            seq2 = temp;
            int tempLength = m;
            m = n;
            n = tempLength;
        }

        // 创建两行滚动数组来保存子问题的解
        int[][] dp = new int[2][n + 1];

        // 动态规划求解最长公共子序列的长度
        for (int i = 1; i <= m; i++) {
            int currRow = i % 2;
            int prevRow = (i - 1) % 2;
            for (int j = 1; j <= n; j++) {
                if (seq1.charAt(i - 1) == seq2.charAt(j - 1)) {
                    dp[currRow][j] = dp[prevRow][j - 1] + 1;
                } else {
                    dp[currRow][j] = Math.max(dp[prevRow][j], dp[currRow][j - 1]);
                }
            }
        }
        return dp[m % 2][n];
    }

    /**
     * 最长公共子序列，空间复杂度O(min(m, n))
     * @param seq1 序列1
     * @param seq2 序列2
     * @return LCS长度
     */
    public static int longestCommonSubsequenceLengthUltra(String seq1, String seq2) {
        int m = seq1.length();
        int n = seq2.length();

        // 确保 n 是较小的值，以减小空间复杂度
        if (m < n) {
            String temp = seq1;
            seq1 = seq2;
            seq2 = temp;
            int tempLength = m;
            m = n;
            n = tempLength;
        }

        // 创建一维数组来保存子问题的解
        int[] dp = new int[n + 1];

        // 动态规划求解最长公共子序列的长度
        for (int i = 1; i <= m; i++) {
            int prev = 0;
            for (int j = 1; j <= n; j++) {
                int current = dp[j];
                if (seq1.charAt(i - 1) == seq2.charAt(j - 1)) {
                    dp[j] = prev + 1;
                } else {
                    dp[j] = Math.max(dp[j], dp[j - 1]);
                }
                prev = current;
            }
        }
        return dp[n];
    }


    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        String seq1 = scanner.next();
        String seq2 = scanner.next();


        // 最长公共子序列，空间复杂度O(mn)
        String lcs = longestCommonSubsequence(seq1, seq2);
        if (!lcs.equals("")) {
            System.out.println("LCS: " + lcs + ", 长度为: " + lcs.length());
        }else {
            System.out.println("0");
        }

        // // 最长公共子序列，空间复杂度2 * O(min(m, n))
        //int res = longestCommonSubsequencesPro(seq1, seq2);
        //System.out.println(res);


         最长公共子序列，空间复杂度O(min(m, n))
        //int res = longestCommonSubsequenceLengthUltra(seq1, seq2);
        //System.out.println(res);
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149

理解最优子结构

最优子结构是指一个问题具有递归结构，并且原问题的最优解可以通过一系列子问题的最优解来构建得到。换句话说，如果一个问题的最优解可以通过其子问题的最优解来推导得出，那么这个问题就具有最优子结构。

最优子结构是动态规划算法中的一个关键概念。在使用动态规划解决问题时，我们将问题划分为若干个子问题，并通过递归地解决子问题来获得原问题的最优解。通过最优子结构的特性，我们可以在求解子问题时将其最优解进行存储，以便后续的计算和使用。

通过将问题划分为子问题，并利用最优子结构的特性，动态规划算法能够避免重复计算，提高效率，并且能够在多项式时间内求解复杂的问题。因此，最优子结构是动态规划算法的一个重要性质，对于设计和分析动态规划算法非常关键。