环形链表的快慢指针相遇的数学证明_快慢指针相遇,慢指针走了多少步

我们说的环形链表是类似于下图的环形链表

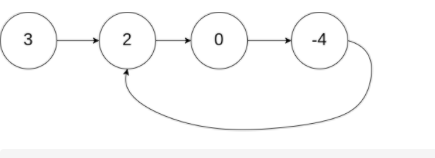
慢指针一圈内必遇上

设我们的环长度为$C$。假定我们慢指针的初始位置是环的入口（比如上图的2），设这个位置为0.
而快指针的初始位置是$A$，$A\in [0,C-1]$。
假设慢指针走了K步之后，快慢指针相遇，则慢指针位置:$0+K$，而快指针的位置是$A+2K$.
此时，显然有一个道理，快指针的初始距离加上它的走过的距离超了慢指针走的距离的$nC$.
所以可以得到表达式$(A+2K)-(0+K)=nC$
进一步化简可得$A+K=nC$，我们令$n=1$时，因为$A\in [0,C-1]$，所以$K$有解，且$K\in [0,C]$，所以，必定在慢指针运行一圈有相遇。

快慢指针相遇时，另一指针从初始点出发，会与慢指针相遇在环的入口

设链表中环外部分的长度为 $a$。$slow$指针进入环后，又走了 $b$的距离与 $fast$ 相遇。此时，$fast$指针已经走完了环的 $n$圈，因此它走过的总距离为 $a+n(b+c)+b=a+(n+1)b+nc$.
根据题意，任意时刻，$fast$ 指针走过的距离都为 $slow$ 指针的 2 倍。因此，我们有

$a+(n+1)b+nc=2(a+b)⟹a=c+(n-1)(b+c)$

有了 $a=c+(n-1)(b+c)$ 的等量关系，我们会发现：从相遇点到入环点的距离加上 $n-1$圈的环长，恰好等于从链表头部到入环点的距离。

因此，当发现 $slow$ 与$fast$ 相遇时，我们再额外使用一个指针 $ptr$。起始，它指向链表头部；随后，它和$slow$ 每次向后移动一个位置。最终，它们会在入环点相遇。

参考资料

LeetCode官方题解