- 1Ambari-2.7.5.0 + HDP-3.1.5.0网盘地址_hdp3.1.5 ubuntu ambari 2.7.5
- 2cesium如何获取立方体的坐标
- 3Typora崩溃 与 设置备份_typora 写多了保存不了
- 4数据挖掘实战(4)——聚类(Kmeans、MiniBatchKmeans、DBSCAN、AgglomerativeClustering、MeanShift)_聚类分析meanshift
- 5除了等保2.0,还有哪些法规涉及云计算数据安全?
- 6最适合Python入门到大牛必看的7本书籍,一定一定一定要收藏!_python高级编程 教材
- 7永磁同步电机(PMSM)无传感器控制基于滑膜观测器Matlab/Simulink仿真分析_永磁同步电机无速度传感器控制 滑膜
- 8python实现ID3算法对鸢尾花数据集分类_机器学习id3算法鸢尾花
- 9这10款VS Code神仙插件,嵌入式程序员必备_vscode嵌入式插件
- 10Redis缓存的使用
排序算法(一) 插入排序和希尔排序_插入排序 希尔排序
赞
踩
一、排序的概念与分类
1.1 排序的概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
1.2 常见的排序算法及分类
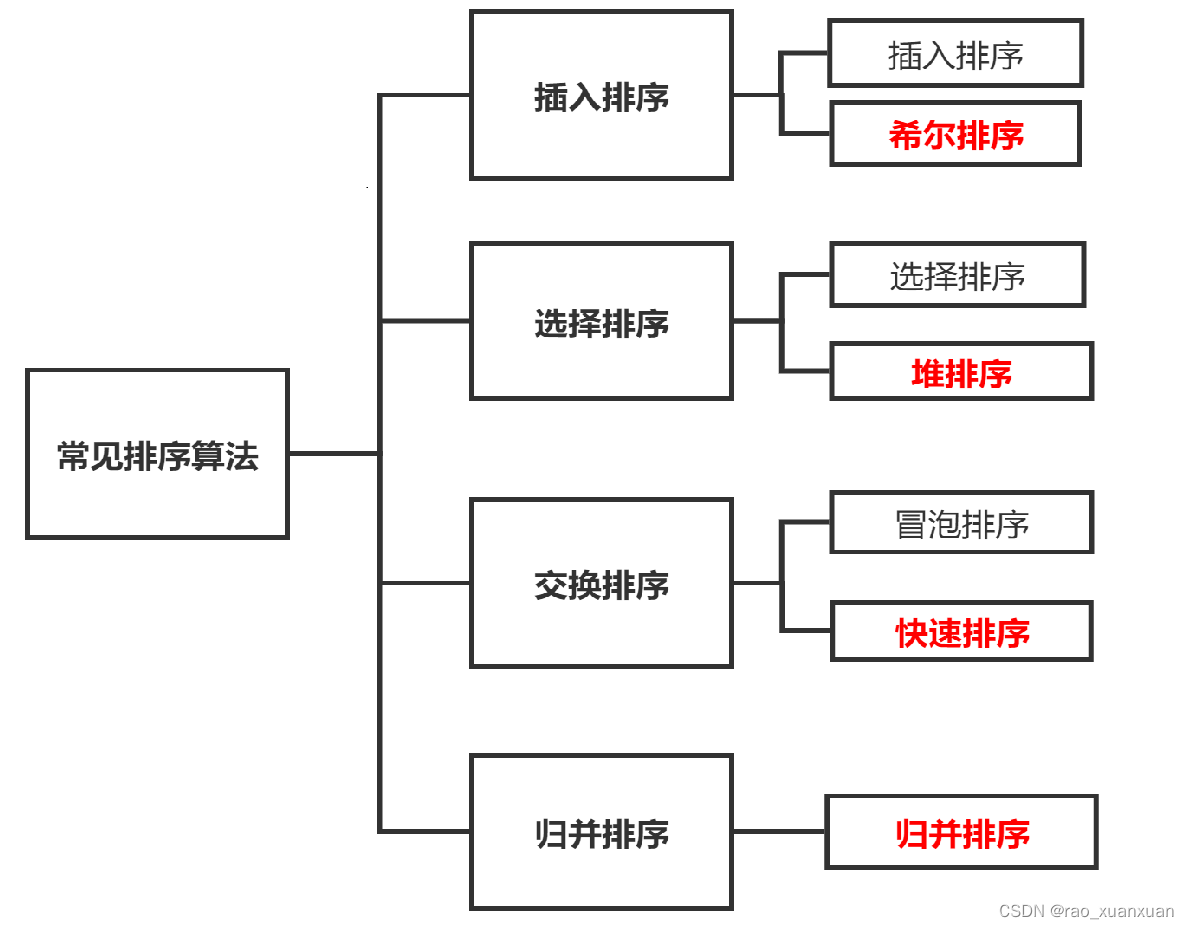
本文介绍插入排序中的插入排序和希尔排序。下面是其他排序算法的博客链接:
二、插入排序
2.1 插入排序的核心思想
对于少量元素的排序,它是一种有效的算法,其工作方式像排序扑克牌。开始时,我们的左手为空且桌子上牌面向下(也就是看不到没有拿到的牌)。然后,我们每次从桌子上拿走一张牌并将它插入到左手中的正确位置,我们从右到左(从小到大)将拿走的牌与已在左手中的每张牌比较,如下图所示。于是拿在左手中的牌总是已经排序好的。

按照上述流程,我们可以得到插入排序数组的大概过程,某次排序key = A[i]时,A[0...i-1]已经排序好,我们只需要找到一个合适的位置x,满足A[x-1] < key < A[x]或是key < A[0],然后将key插入到相应位置处。一直重复直到 i = A.length-1,此时,数组A便已经有序。
2.2 插入排序的伪代码及流程
用A表示待排序的数组,插入排序的伪代码如下:

其中,用j来表示当前需要插入的元素的下标(这里假定数组下标从0开始),key表示要插入元素的值,即key=A[j]。我们结合下图来理解插入排序的具体流程和细节。
如下图:第一次排序,j=1,也就是要将key = A[1] = 2插入已经排序好的子数组A[0]中,按照伪代码的流程,如图(a),我们从i = j - 1处开始寻找合适的插入点,A[i] > key,说明当前位置不满足,于是将i后移一位,即A[i+1] = A[i](注意到key所在位置被覆盖,为了之后可以使用A[j],我们使用key在进行插入之前记录下A[j]的值),如图(b);继续判断下一个位置(i--)是否满足插入条件,由于i < 0(退出while循环的一个条件),于是可以将key插入到【i+1】处,即A[i+1] = key,如图(c),本次插入完成。

如下图:第二次排序,j=2,也就是要将key = A[2] = 5插入到已经排序好的子数组A[0:1]中,按照伪代码的流程,如图(a),我们从i = j-1处开始寻找合适的插入点,A[i] > key,说明当前位置不满足,于是将A[i]后移,即A[i+1] = A[i],如图(b);继续判断下一个位置(i--)是否满足插入条件,由于A[i] < key(退出while循环的一个条件),于是可以将key插入到【i+1】处,即A[i+1] = key,如图(c),本次插入完成。
如下图:第三次排序, j = 3,也就是要将key = A[3] = 6插入到已经排序好的子数组A[0:2]中,按照伪代码的流程,如图(a),我们从i = j-1处开始寻找合适的插入点,由于A[i] < key(退出while循环的一个条件),满足插入条件,于是将key插入到【i+1】处,即A[i+1] = key,如图(b),本次插入完成。

按照以上规律,我们重复操作,直到 j = A.length-1,即最后一个元素完成插入,此时数组A排序完成。
2.3 插入排序的具体代码
- void insertSort(int* nums, int numsSize)
- {
- for (int j = 1; j < numsSize; j++) {
- int key = nums[j];
- int i = j - 1;
- while (i >= 0 && nums[i] > key){
- nums[i + 1] = nums[i];
- i--;
- }
- nums[i + 1] = key;
- }
- }
2.4 插入排序的循环不变式和正确性分析
根据之前的分析,在for循环(循环变量为j)的每次迭代开始,子数组A[0....j-1]构成了当前在手上的牌,也就是已经有序,实际上,A[0....j-1]就是原来在位置0到j-1上的元素,现在已经按序排列;而子数组A[j+1.....A.length-1]对应仍在桌上的牌堆,即未排序元素,我们将A[0....j-1]的这些性质称为循环不变式。接下来证明循环不变式的三条性质(记n = A.length)。
1.初始化。首先证明在第一次迭代前(j=1)时,循环不变式成立。子数组仅有A[0]一个元素组成,就是A[0]原来的元素,所以子数组显然是有序的,满足循环不变式。
2.保持。其次证明每次迭代保持循环不变式。for循环的4-7行将A[j-1]、A[j-2]等元素向右移动一个位置,直到找到合适的位置,在第8行将插入key插入该位置。此时,子数组A[0....j]由原来在A[0...j]中的元素组成,并且已经按序排列。于是对for循环的下一次迭代增加 j 将保持循环不变式的正确性。
3.终止。最后研究当循环结束时的情况。因为每次循环迭代j增加1,那么for循环结束时必然有j = n。在循环不变式中将 j 用 n 替代,有子数组A[0....n-1]有原来A[0....n-1]的元素组成,注意到子数组A[0....n-1]就是整个数组A,因此整个数组已经完成排序。插入排序的正确性得证。
2.5 插入排序的性能分析
空间复杂度:由于插入排序不需要开辟额外空间存储数组,只需要key等变量记录相关信息,时间复杂度为常数O(1)。
时间复杂度:考虑最坏的情况,数组反向排序,即已经递减排序,那么对于每个key,都需要经历最多次数的比较,对于 j = 1,2, ... , A.length-1,将A[j]插入到子数组A[0...j-1]中,消耗时间都为:c*j,排序总耗时为: 。因此插入排序的时间复杂度为O(n^2)。
稳定性:对于相等的元素,由while循环的条件可知并不会改变位置,因此插入排序是一种稳定的算法。
三、希尔排序
3.1 希尔排序的核心思想
希尔排序是对插入排序的优化,又称缩小增量排序。其基本思想是:先选定一个整数gap,将待排序数组分组,对各组进行排序,这一过程称为预排序,使得数组接近有序。经过若干次预排序后进行插入排序,得到的就是有序的数组。这样,针对数组逆序的最坏情况,排序的效率得到极大的提高。
3.2 希尔排序的流程
首先,选取分组间隔gap,这里我们选取gap = 3,对数组A进行分组,如图(a)。然后,对每组数进行插入排序,如图(b)。此时,经过一次预排序,数组中大的元素已经移动到靠后位置,小的数已经移动到靠前的位置,数组已经接近有序。

之后,减小gap,继续进行预排序。第二次分组排序,取gap = 2,对数组A进行分组,如图(a)。然后,对每组数进行插入排序,如图(b)。此时,经过两次预排序,数组的有序程度已经很高。

之后,减小gap,取gap = 1,此时就相当于不分组直接对整个数组进行插入排序,如图(a)。对整个数组排序完后,得到的就是有序的数组,如图(b)。

3.3 希尔排序的具体代码
首先,我们确定gap的选择方式,其实gap只要满足每次递减并且最终为1即可,这里我们让gap从A.length/2开始,每次分组排序后gap减小为原来的一半,即gap/=2。
具体实现代码的过程很简单,由于每次进行的都是插入排序,因此我们只需要在前面插入排序代码的基础上做出修改。分组排序插入与直接插入排序的唯一区别就是每个元素的距离,在分组插入排序时,每两个需要比较的元素下标之差为gap,而直接插入排序每两个需要比较的元素下标之差为1,于是,我们只需要将插入排序中的1替换为gap即可得到分组排序的代码。对于gap的变化,我们采用while循环,每次在入while循环后先确定gap(gap /= 2),然后根据gap进行分组排序,于是while循环终止的条件是while>1。
- void shellSort(int* nums, int numsSize)
- {
- int gap = numsSize;
- while (gap > 1)
- {
- gap /= 2;
- for (int j = gap; j < numsSize; j++) {
- int key = nums[j];
- int i = j - gap;
- while (i >= 0 && nums[i] > key) {
- nums[i + gap] = nums[i];
- i -= gap;
- }
- nums[i + gap] = key;
- }
- }
- }

3.4 希尔排序的性能分析
空间复杂度:类似于插入排序,由于希尔排序不需要开辟额外空间存储数组,只需要key、gap等变量记录相关信息,时间复杂度为常数O(1)。
时间复杂度:希尔排序的时间复杂度分析极其复杂,这里给出相关结论:希尔排序的时间消耗主要取决于增量(gap)的变化,因此希尔排序的时间复杂度与增量序列高度相关,以下列举几个经典增量序列:
稳定性:希尔排序是一种不稳定的排序算法。


