卷积和全连接层的模型参数计算详解，详细到神经元个数一个个算，天啊，以VGG16为例_全连接层计算

神经网络参数计算基础（卷积、全连接层）

卷积核参数量计算

单个卷积核大小

一个卷积核的大小是 kernel = channel(input) × kernel_width × kernel_height，如下图卷积过程，一个卷积核能卷积得到一个通道的特征图。

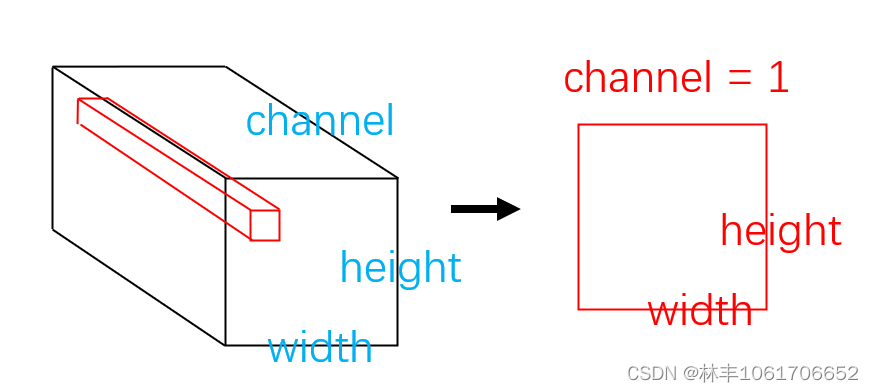
其中，channel(input) 就是输入的通道数，kernel_width，kernel_height 分别表示一个卷积核的宽和高。通过一个这么大的卷积核对一层多通道的特征图层进行卷积我可以获得一个（1，W，H）的特征图层。
如果需要输出 N 个通道的特征图层，我们就需要 N 个这样的卷积核进行卷积计算，即可获取（N，W，H）的特征图层。这里的 N 个卷积核在建立网络的时候都是系统自动初始化的，如随机初始化，全部为0初始化，高斯分布初始化等，看你的库是用什么方法初始化。

卷积层卷积核大小的计算

由上面的说明，我们可以知道，一个卷积层的卷积核参数量计算其实就受输入通道、输出通道、卷积核大小的影响，而实际卷积过程中我们还会给每个卷积核都加个偏置，因此公式如下：
卷积核参数量
= kernel.shape × kernel.num + bias.num
= ( channel(input) × kernel_width × kernel_height ) × channel(output) + channel(output)

其中，channel(input) 是输入卷积层的通道数，channel(output)是输出卷积层的通道数。
也就是说，如果输入的特征图层的 shape 是（3，224，224），需要 3 × 3 卷积之后****输出的特征图层的 shape 是（64，224，224）。我们就可以知道输入通道数为 3，输出通道数为64，kernel_width 为 3，kernel_height 为 3，因此，我们可以计算这个 3 × 3 卷积层的卷积核参数量大小为
参数量 = 3 × 3 × 3 × 64 + 64 = 1792。

全连接层参数计算

全连接层概念

全连接层其实就是一个权重矩阵，计算过程其实就是通过一个矩阵，将一个向量转换成另外一个维度的向量。公式如下：
Vector(output) = Vector(input) × Weight(FC) + Bias(FC)
其中，Weight(FC) 表示全连接层的权重，Bias(FC)表示全连接层的偏置。
也就是说，如果输入全连接层向量的 shape 是（1，4），输出全连接层向量的 shape 是（1，3），显然学过线性代数的同学就知道了，这个全连接层权重的 shape 是（4，3），偏置的shape是（1，3）。如输入一个（2，2，2，2）的四维向量，需要输出一个三维向量，当权重矩阵的数值全为1，偏置矩阵的数值全为3时，计算过程如下：

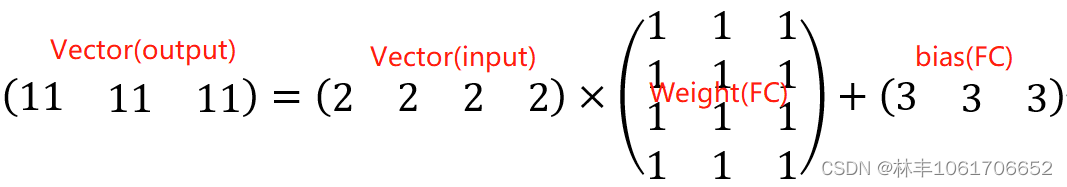
全连接层参数计算

全连接层的参数量，其实就是参数权重和偏置的大小。因此全连接层的参数量就有公式：
全连接层参数量
= Weight(FC).height × Weight(FC).width + bias(FC).width
= Vector(input).shape × Vector(output).shape + Vector(output).shape
因此，如上面的例子，输入是1×4的向量，输出是1×3的向量，全连接层的参数量 = 4 × 3 + 3 = 15。

VGG16参数计算

模型架构

VGG16就是下图红框部分，我加上了在这里面的特征图层的大小。因此VGG16输入的大小是（224，224，3），最后一层的输出是（1000）。

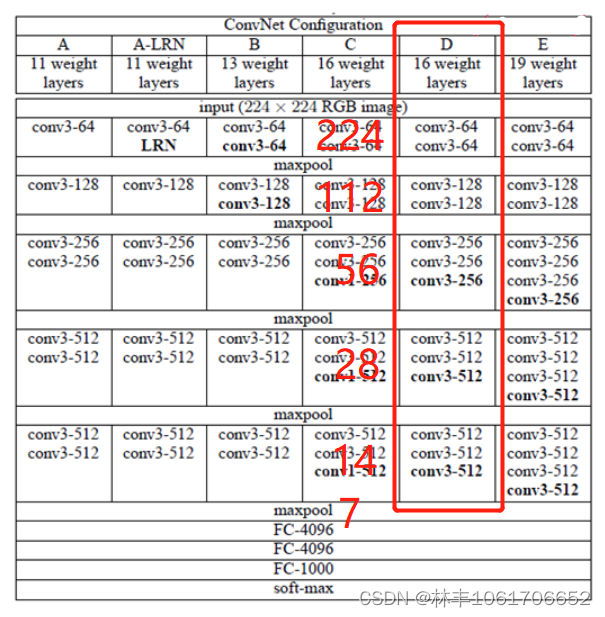
计算参数量

第一部分卷积层

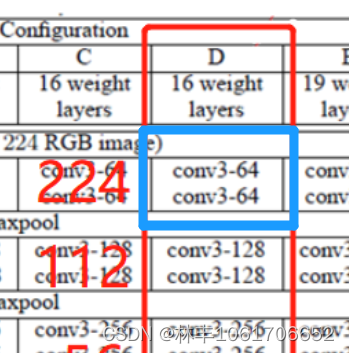
第一部分就是蓝色框的位置，其中有两个3*3的卷积层：

1. 第一个卷积层把输入（224，224，3）的图片转换成（224，224，64）的特征图层；
2. 第二个卷积层把（224，224，64）的特征图层转换成（224，224，64）的特征图层；

num11表示第 1 部分的第 1 个卷积核，num12表示第 1 部分的第 2 个卷积核，后面以此类推。
根据上述公式我们可以知道第一层卷积的参数量为
num11 = 3×3×3×64 + 64 = 1792
第二层卷积的参数量为
num12 = 64×3×3×64 + 64 = 36928

其他卷积层参数量计算

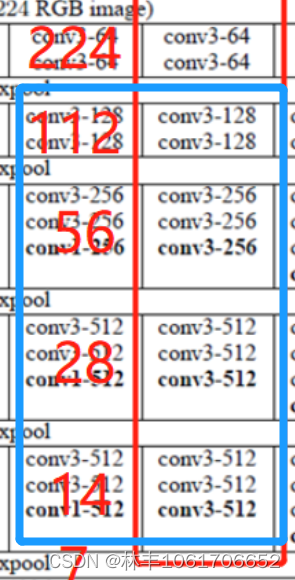
num21 = 64 × 128 × 3 × 3 + 128 = 73856
num22 = 128 × 128 × 3 × 3 + 128 = 147,584
num31 = 128 × 256 × 3 × 3 + 256 = 295,168
num32 = 256 × 256 × 3 × 3 + 256 = 590,080
num33 = 256 × 256 × 3 × 3 + 256 = 590,080
num41 = 256 × 512 × 3 × 3 + 512 = 1,180,160
num42 = 512 × 512 × 3 × 3 + 512 = 2,359,808
num43 = 512 × 512 × 3 × 3 + 512 = 2,359,808
num51 = 512 × 512 × 3 × 3 + 512 = 2,359,808
num52 = 512 × 512 × 3 × 3 + 512 = 2,359,808
num53 = 512 × 512 × 3 × 3 + 512 = 2,359,808
即所有卷积层的参数总量为
num_conv_total = 14,714,688

全连接层输入说明

全连接层是整个模型中参数量占比较多的一部分，我们计算蓝框这一部分的全连接层。

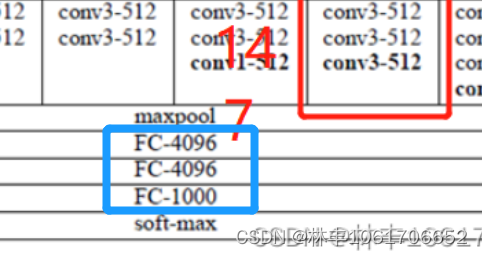
首先我们看全连接层上面的maxpool，通常这种maxpool操作后直接展平为一维向量输入进全连接层（展平：其实就是将（m，n）的向量变成（1，m×n）的向量）。
因此，我们需要知道上一层的特征图层大小是多少，根据推算，maxpooling后的特征图大小是 7 × 7 × 512，即可直接展平成（1，7×7×512）大小的向量，即（1，25088）的向量。

全连接层计算参数量

根据上述全连接层的参数量计算公式，可知各个全连接层的参数量是：
num_fc1 = 25088 × 4096 + 4096 = 102,764,544
num_fc2 = 4096 × 4096 + 4096 = 16,781,312
num_fc3 = 4096 × 1000 + 1000 = 4,097,000
即所有的全连接层参数量为
num_fc_total = 123,642,856

其他部分参数量

其他部分如maxpool，softmax等，我记得是没有参数，所以为0。
VGG16总体参数量为 num_total = num_conv_total + num_fc_total = 138,357,544
即VGG16的参数计算就算完啦。

验证

我用torch调用VGG16看下模型大小的时候发现，跟计算出来的结果相差了很多。

然后就去看了下他的源码，看是不是模型设置跟论文的不一样，发现除了最后的maxpooling换成了平均池化，加了dropout层，其他没什么大的变化。




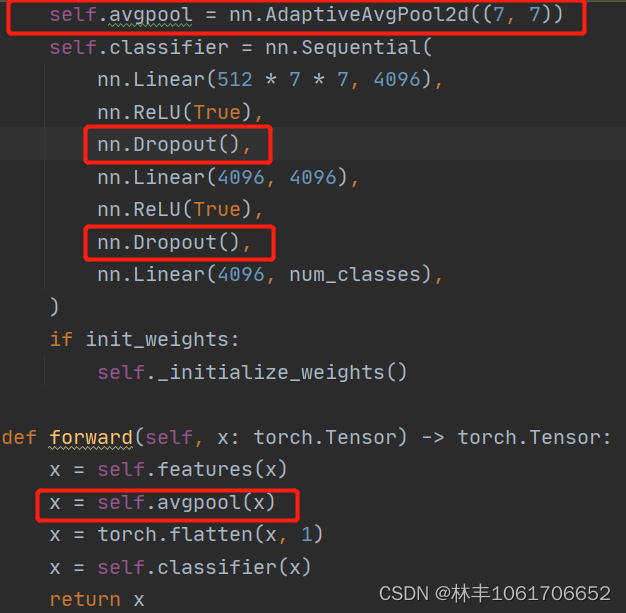
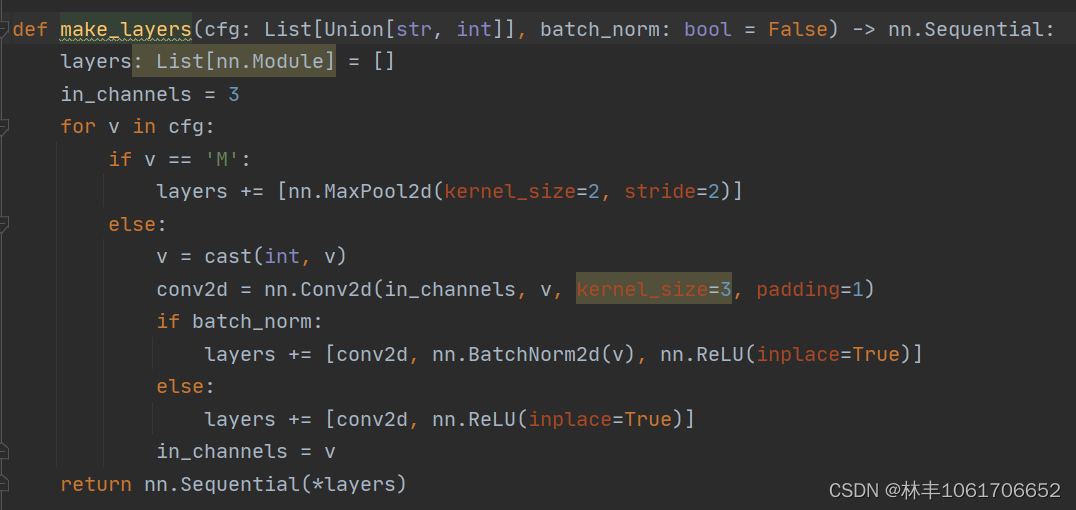
后面发现是自己傻逼了，我们的计算参数量是138,357,544，也就是138M，保存成文件，需要用4bytes的float类型来存储，
所以保存后的模型大小是138357544 × 4 = 553,430,176，就是553M，验证完毕。
而实际保存的参数量为540M。
个人想法是由于dropout层去除了一些参数量，所以容量减小了，以上。

个人学习，如有不正，请大佬指正，欢迎交流。