【FinE】在险价值(VaR)计算_在险价值var计算公式

VaR模型

在险价值Value-at-risk的定义为，在一定时期$\Delta t$内，一定的置信水平$1-\alpha$下某种资产组合面临的最大损失，公式为
$$P(\Delta p\le VaR)=1-\alpha$$
在持有组合时期$\Delta t$内，给定置信水平$1-\alpha$下，该组合的最大损失不会超过VaR，使用VaR进行风险衡量时，需要给定持有期和置信水平，巴塞尔协会规定持有期标准为10天，置信水平为99%，商业银行可以确定各自的水平，J.P.Morgan公司在1994年年报中设置持有期为1天，置信水平为95%，VaR值为1500万元，即J.P.Morgan公司在一天内所持有的风险头寸损失小于1500万的概率为95%.

VaR的主要性质：

• 变换不变性：$VaR(X+a)=VaR(X)+a,a\in \mathbb{R}$
• 正齐次性：$VaR(aX)=aVaR(X),a<0$，资产的风险与持有头寸呈反比关系
• 协单调可加性：$VaR(X_1+X_2)=VaR(X_1)+VaR(X_2)$
• 不满足次可加性和凸性：不满足次可加性表示资产组合的风险不一定小于各资产风险之和，这个性质导致VaR测度存在不合理性，因为组合VaR不可以通过求各个资产的VaR得出。不满足凸性表示以VaR为目标函数的规划问题一般不是凸规划，局部最优解不一定是全局最优解，由于多个局部极值的存在导致无法得到最优资产组合
• 满足一阶随机占优
• VaR关于概率水平$1-\alpha$不是连续的

VaR对风险的衡量具有前瞻性，将预期损失的规模和发生的概率结合，可以了解在不同置信水平上风险的大小.
但是VaR模型是对正常市场环境中金融风险的衡量，如果整体环境出现了动荡或者发生极端情况时，VaR就会失去参考价值，一般加上压力测试（Stress Test）结合极值分析进行风险衡量，常用的极值分析方法有BMM和POT两种，极值分析就是当风险规模超过设定阈值时进行建模，处理风险尾部.
由于金融数据的低信噪比特点，导致数据呈现尖峰后尾的分布，这种分布导致VaR模型无法产生一致性度量，针对风险度量的不一致性可以使用条件风险价值CVaR模型修正，即当资产组合损失超过给定的VaR值时，资产组合的损失期望，计算公式如下
$$CVa{R}_{\alpha }=\mathbb{E}(-X\mid -X\le Va{R}_{\alpha }(x))$$
其中$X$表示资产的损益，CVaR满足以下性质：

• 一致连续性
• 次可加性，$\forall X,Y$满足$\rho (X+Y)\le \rho (X)+\rho (Y)$
• 满足二阶随机占优
• 满足单调性，$\forall X\le Y$满足$\rho (X)\le \rho (Y)$

案例：AAPL

历史模拟法

历史模拟法计算AAPL公司的VaR，历史模拟法使用市场历史因子的变化来估计市场因子未来的变化，对市场因子的估计采用权值估计方法，根据市场因子的未来价格水平对头寸进行重新估值，计算出头寸的价值变化，将组合损益从小到大排序，得到损益分布，通过计算给定置信度下的分位数求出VaR. 这里计算了置信水平分别为95%和99%的VaR.

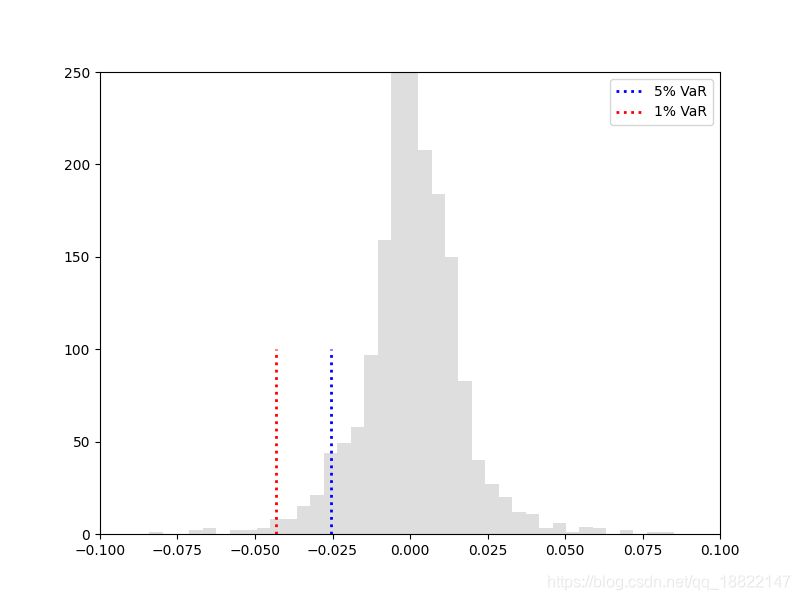
历史模拟法python代码

import pandas_datareader.data as web
import datetime as dt
import pandas as pd
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt

start=dt.datetime(2012, 1, 1)
end=dt.datetime(2018, 12, 31)
df=web.DataReader('AAPL', 'yahoo', start, end)

# 对数收益率
df['return']=np.log(df['Adj Close']/df['Adj Close'].shift(1))
# 计算收益率的分位数
# 5%分位数
VaR5=np.percentile(df['return'].dropna(), 5)
# 1%分位数
VaR1=np.percentile(df['return'].dropna(), 1)

def hm_demo():
    grey = 0.75, 0.75, 0.75
    fig=plt.figure(figsize=(8, 6))
    plt.hist(df['return'], bins=50, alpha=0.5, color=grey)
    plt.plot([VaR5, VaR5], [0, 100], 'b:', linewidth=2, label='5% VaR')
    plt.plot([VaR1, VaR1], [0, 100], 'r:', linewidth=2, label='1% VaR')
    plt.xlim([-0.1, 0.1])
    plt.ylim([0, 250])
    plt.legend()
    # plt.savefig('hm_var.png')
    plt.show()

hm_demo()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

参数模型分析法

分析法利用证券组合的价值函数与市场因子之间的近似关系，推断市场因子的统计分布，简化VaR计算.
使用参数模型分析法需要进行数据预处理工作，在Matlab(R 2012a)中常用数据预处理函数如下

% 计算股票样本的均值，标准差，相关性与beta
% 价格转收益率
tick_ret=tick2Ret(stockPrices, [], 'continuous')
mu=mean(tick_ret) % 计算均值
std=std(tick_ret) % 计算标准差
mdd=maxdrawdown(tick_ret) % 计算最大回撤
coef=corrcoef(tick_ret) % 相关系数矩阵
1
2
3
4
5
6
7

tick2ret函数说明

[RetSeries, RetIntervals]=tick2ret(TickSeries, TickTimes, Method)
INPUT
TickSeries: 价格序列
TickTimes: 时间序列
Method: 计算方法，continuous表示对数收益率计算log(x)-log(y)；simple表示简单收益率计算(x-y)/y
OUTPUT
RetSeries: 收益率序列
RetIntervals: 收益率对应的时间间隔
1
2
3
4
5
6
7
8

maxdrawdown函数说明

T日组合最大回撤计算接口为
[MaxDD, MaxDDIndex]=maxdrawdown(Data, Format)
INPUT
Data: 组合每日总收益序列
Format: 类别有 return(默认，收益率序列)，arithmetic（算术布朗运动），geometric（几何布朗运动）
OUTPUT
MaxDD：最大回撤值
MaxDDIndex：最大回撤值位置
1
2
3
4
5
6
7
8

参数模型法计算VaR使用接口portvrisk，函数说明如下

ValueAtRisk=portvrisk(PortReturn, PortRisk, RiskThreshold, PortValue)
INPUT
PortReturn：组合收益率
PortRisk: 组合标准差
RiskThreshold：置信度阈值，默认为5%
PortValue：组合资产价值，默认为1
OUTPUT
ValueAtRisk：风险价值
1
2
3
4
5
6
7
8

参数模型法计算程序如下

pVar=portvrisk(mean(ret), std(ret), [0.01, 0.05], port_value);
confidence=pVar/port_value
1
2

非参数bootstrap

对历史数据进行有放回的采样，计算每次采样的VaR，然后对所有采样结果求期望，设置采样容量为300，进行200轮采样的结果如下

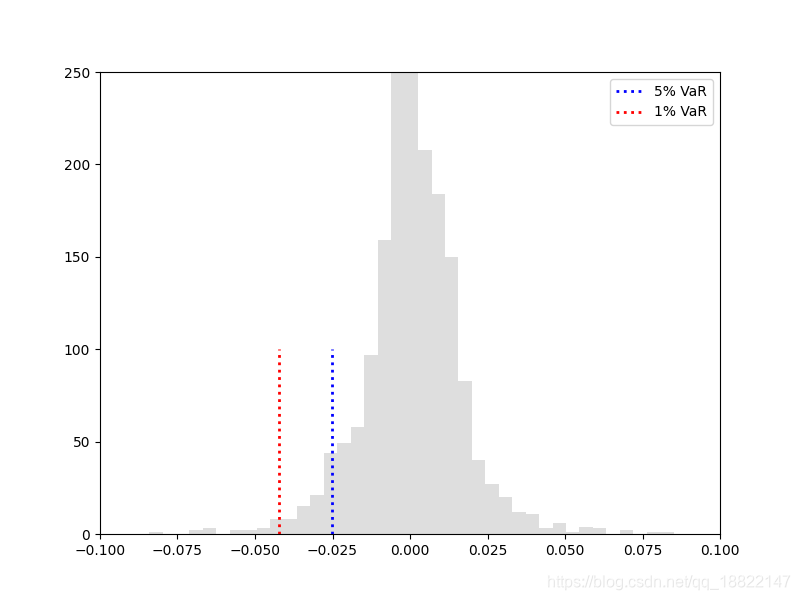
python非参数bootstrap代码

def bootstrap_demo():
    ret=df['return'].dropna()
    # 有放回采样
    def sample(data, size):
        sample=np.random.choice(data, size, replace=True)
        VaR5=np.percentile(sample, 5)
        VaR1=np.percentile(sample, 1)
        return (VaR5, VaR1)

    sz, n=300, 200
    samples=np.array([sample(ret, sz) for _ in range(n)])
    VaR5, VaR1=np.mean(samples, axis=0)
    
    grey = 0.75, 0.75, 0.75
    fig=plt.figure(figsize=(8, 6))
    plt.hist(df['return'], bins=50, alpha=0.5, color=grey)
    plt.plot([VaR5, VaR5], [0, 100], 'b:', linewidth=2, label='5% VaR')
    plt.plot([VaR1, VaR1], [0, 100], 'r:', linewidth=2, label='1% VaR')
    plt.xlim([-0.1, 0.1])
    plt.ylim([0, 250])
    plt.legend()
    plt.savefig('bootstrap_var.png')
    plt.show()

bootstrap_demo()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

Monte-Carlo模拟计算

Monte-Carlo计算欧式期权价格可以见这篇博客.
Monte-Carlo模拟的基本步骤是：
1.选择市场因子变化的随机过程和分布，估计该过程的参数的相关参数.
2.模拟市场因子的变化路径，建立对市场因为未来的预测
3.对市场因子每个情景，利用公式计算价值和变化
4.根据组合价值变化分布模拟结果，计算给定置信度下的VaR.
设置股票价格符合几何布朗运动，即
$$S_{t+1}=S_t\exp ((\mu -\frac{{\sigma }^2}{2})\Delta t+\sigma \epsilon \sqrt{\Delta t})$$
其中$\mu$为收益率均值，${\sigma }^2$为收益率方差，$\epsilon$为从Gaussian分布中抽样出的随机值.
计算$\Delta t=1$日的VaR值

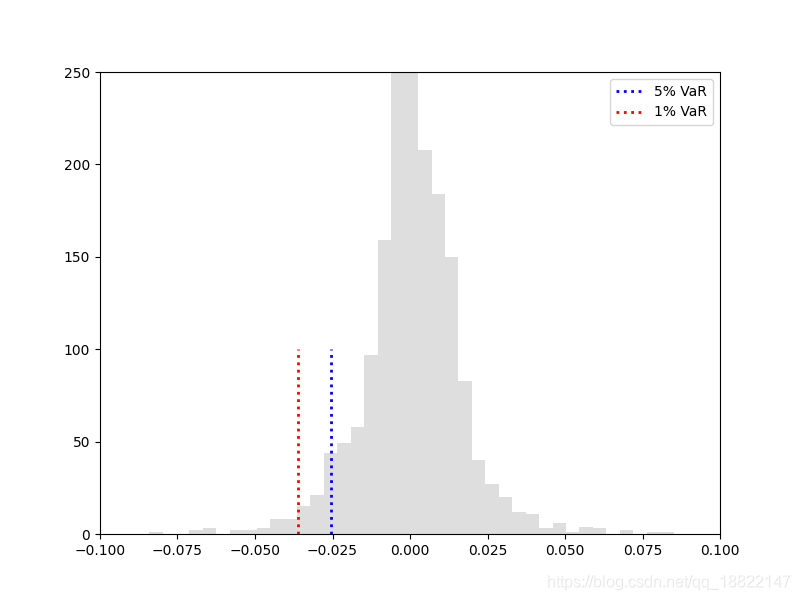
python蒙特卡洛模拟计算代码

def monte_carlo_demo():
    ret = df['return'].dropna()
    mu, sig = np.mean(ret), np.std(ret)
    def gbm(s0, T, n):
        dt=T/n
        price=s0
        for _ in range(n):
            eps=np.random.normal()
            s=price*np.exp((mu-sig**2/2)*dt+sig*eps*np.sqrt(dt))
            price=s
        return price

    sp=[]
    s0=1
    for _ in range(10000):
        sp.append(gbm(s0, 1, 100))
    sret=np.array(sp)/s0-1
    VaR1=np.percentile(sret, 1)
    VaR5=np.percentile(sret, 5)
    print(VaR1, VaR5)
    grey = 0.75, 0.75, 0.75
    fig=plt.figure(figsize=(8, 6))
    plt.hist(df['return'], bins=50, alpha=0.5, color=grey)
    plt.plot([VaR5, VaR5], [0, 100], 'b:', linewidth=2, label='5% VaR')
    plt.plot([VaR1, VaR1], [0, 100], 'r:', linewidth=2, label='1% VaR')
    plt.xlim([-0.1, 0.1])
    plt.ylim([0, 250])
    plt.legend()
    plt.savefig('monte-carlo_var.png')
    plt.show()

monte_carlo_demo()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

$k$天的VaR可以根据公式
$$Va{R}_k=Va{R}_1\ast \sqrt{k}$$
计算，或者令程序中gbm参数T=k进行模拟计算.

参考资料

DCC-Garch VaR 量化小白H
Copula模型估计组合VaR 量化小白H
python金融实战之计算VaR
Risk Analysis in Python
量化投资以Matlab为工具 中国工信出版集团 李洋 郑志勇