基于SVM-支持向量机对鸢尾花数据进行分类_cnn-svm 莺尾花

 目录

认识SVM——支持向量机

 SVM的"硬间隔"与"软间隔"

 实战——SVM对鸢尾花分类

认识SVM——支持向量机

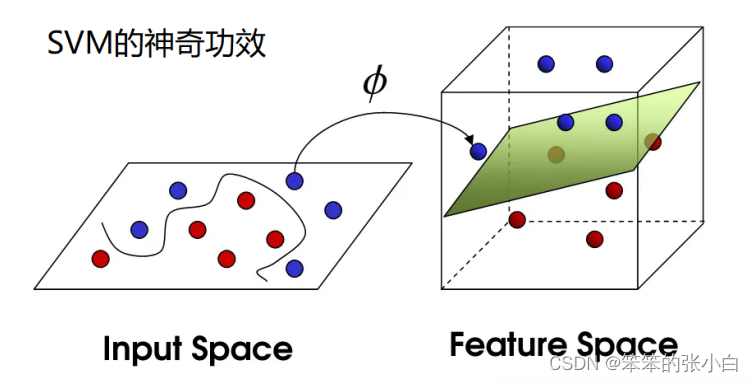
什么是支持向量机

支持向量机（SVM），Supported Vector Machine,基于线性划 分，输出一个最优化的 分隔超平面，该超平面不但能将两类正确分开,且使分类间隔 (margin)最大 

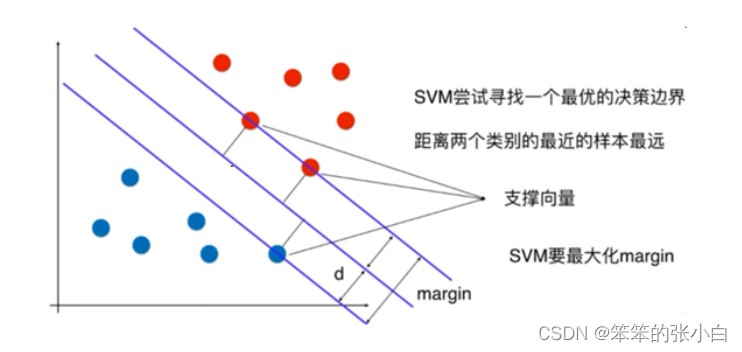
•  所有训练数据点距离最优分类超平面的距离都要大于支持向量距 离此分类超平面的距离
• 支持向量点到最优分类超平面距离越大越好

 注意： SVM的终极目标是求出一个最优的线性分类超平面

 SVM的核函数

        当在低维空间中，不能对样本线性可分时，将低维空间中的点 映射到高维空间中，使 它们成为线性可分的，再使用线性划分的原理来判断分类边界。 这里有个问题：如果直接采用这种技术在高维空间进行分类或 回归，可能在高维特征 空间运算时出现"维数灾难"！采用核函数技术(kernel trick)可以有效 地解决这样的问题 直接在低维空间用核函数，其本质是用低维空间中的更复杂的 运算代替高维空间中的普 通内积。

常用的核函数

• linear：线性核函数 当训练数据线性可分时，一般用线性核函数，直接实现可分
• poly：多项式核函数
• rbf：径向基核函数/高斯核函数（Radial Basis Function Kernel） gamma值越小，模型越倾向于欠拟合 gamma值越大，模型越倾向于过拟合
• sigmod：sigmod核函数

 SVM的"硬间隔"与"软间隔"

硬间隔

当支持向量机（SVM）要求所有样本都必须划分正确，这称为 “硬间隔”（hard margin）。 

软间隔

到目前为止，我们一直假定存在一个超平面能将不同类的样本 完全划分开。然而，在现 实任务中往往很难确定合适的核函数使得训练样本线性可分（即使 找到了，也很有可能 是在训练样本上由于过拟合所造成的） 缓解该问题的一个办法是允许支持向量机在一些样本上出错， 这称为"软间隔"（soft margin）。 

 软间隔支持向量机的数学表达式为（L1正则）：

 或者（L2正则）

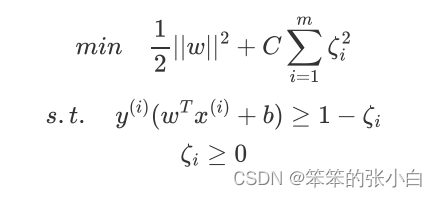
 注意： 正则项前面的常数C，C越大说明相应的容错空间越小，若C 取正无穷，则"逼迫"着每个ζ（也称为“松弛变量”）都必须等于 0，此时的Soft Margin SVM就变成了Hard Margin SVM.

 实战——SVM对鸢尾花分类

在sklearn中可通过sklearn.svm.SVC使用支持向量机的方式分类 本节课使用SVC对两种鸢尾花的类型进行分类

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
 
iris = datasets.load_iris()  # 加载鸢尾花数据集
X = iris.data  # 样本特征
y = iris.target  # 样本标签
X = X[y<2,:2]  # 选择前两种花，为了可视化，只选择前两个特征
y = y[y<2]
plt.scatter(X[y==0,0],X[y==0,1],color='red')
plt.scatter(X[y==1,0],X[y==1,1],color='blue')
plt.show()

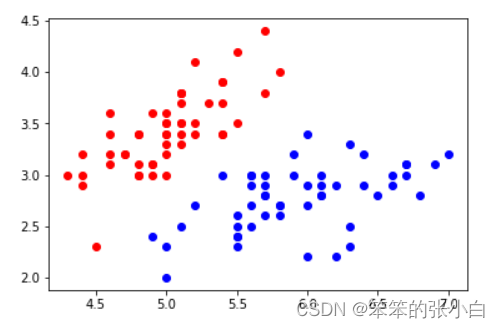
from sklearn.model_selection import train_test_split
# 拆分数据集
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=666)
from sklearn.preprocessing import StandardScaler
 
# 标准化样本特征
std = StandardScaler()
X_train_std = std.fit_transform(X_train)
X_test_std = std.transform(X_test)
 
# 使用SVC分类
from sklearn.svm import SVC
 
# 使用rbf核函数，相应地设置rbf核函数的gamma参数，C是正则化参数
svc = SVC(C=1.0,kernel="rbf",gamma=1.0)
svc.fit(X_train_std,y_train)  # 训练样本集上拟合
svc.score(X_test_std,y_test)   # 测试样本集上测试分类准确率

准确率100%