devbox
我家小花儿
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

【数据结构】树与二叉树、树与森林部分习题与算法设计例题

作者：我家小花儿 | 2024-04-17 10:48:18

赞

踩

【数据结构】树与二叉树、树与森林部分习题与算法设计例题

目录

  1. 树与二叉树知识点文章: 【数据结构】树与二叉树（递归法先序、中序、后序、层次遍历二叉树、二叉树的建立以及求树高的方法）
  2. 二叉树遍历算法的应用: 【数据结构】树与二叉树遍历算法的应用（求叶子节点个数、求树高、复制二叉树、创建二叉树、二叉树存放表达式、交换二叉树每个结点的左右孩子）
  3. 树与森林知识点文章: 【数据结构】树与森林（树的存储结构、森林与二叉树的转化、树与森林的遍历）

【数据结构】树与二叉树部分习题与算法设计例题

一、单选题

  1. 设树T的度为4,其中度为1,2,3和4的结点个数分别为4,2,1,1 则T中的叶子数为( )。

A. 5
B. 6
C. 7
D. 8
选D
一棵含有n个结点的树，有n-1个分支，即 n = 1 ∗ 4 + 2 ∗ 2 + 3 ∗ 1 + 4 ∗ 1 + 1 = 16 ; n = 1*4 + 2*2 + 3*1 + 4*1 + 1 = 16; n=1∗4+2∗2+3∗1+4∗1+1=16;
又由于 n = n 0 + n 1 + n 2 + n 3 + n 4 = n 0 + 8 ; n = n_0 + n_1 + n_2 + n_3 + n_4 = n0 + 8; n=n0​+n1​+n2​+n3​+n4​=n0+8;
n 0 + 8 = 16 n_0 + 8 = 16 n0​+8=16，所有叶子结点个数为8

  1. 在下述结论中,正确的是( )
    ①只有一个结点的二叉树的度为0;
    ②二叉树的度为2;
    ③二叉树的左右子树可任意交换;
    ④深度为K的完全二叉树的结点个数小于或等于深度相同的满二叉树。

A 1、2、3

B 2、3、4

C 2、4

D 1、4
选D
(1)对。只有一个结点的二叉树的度为0;
(2)二叉树的要求是度不超过2
(3) 二叉树是有序树，左右子树不能交换位置.
(4)对。深度为K的完全二叉树的结点个数小于或等于深度相同的满二叉树。

  1. 设森林F对应的二叉树为B,它有m个结点,B的根为p,p的右子树结点个数为n,森林F中第一棵树的结点个数是( )

A m-n

B m-n-1

C n+1

D 条件不足,无法确定
选A
所有节点数减去右兄弟，剩下的就是第一棵树。

  1. 若一棵二叉树具有10个度为2的结点,5个度为1的结点,则度为0的结点个数是( )

A 9

B 11

C 15

D 不确定
选B
性质3：*对任何一棵二叉树，若它含有 n 0 n_0 n0​个叶子结点、 n 2 n_2 n2​个度为 2的结点，则必存在关系式 n 0 = n 2 + 1 n_0=n_2+1 n0​=n2​+1。
n 0 = n 2 + 1 = 10 + 1 = 11 n_0=n_2+1=10+1=11 n0​=n2​+1=10+1=11

  1. 在一棵三叉树中度为3的结点数为2个, 度为2 的结点数为1个,度为1的结点数为2个,则度为0的结点数为( )个

A. 4

B. 5

C. 6

D. 7
选c
设该树总共有n个节点,则 n = n 0 + n 1 + n 2 + n 3 . n=n_0+n_1+n_2+n_3. n=n0​+n1​+n2​+n3​.
该树中除了根节点没有前驱以外,每个节点有且只有一个前驱,因此有n个节点的树的总边数为 n − 1 n-1 n−1条.根据度的定义,总边数与度之间的关系为： n − 1 = 0 ∗ n 0 + 1 ∗ n 1 + 2 ∗ n 2 + 3 ∗ n 3 . n-1=0*n_0+1*n_1+2*n_2+3*n_3. n−1=0∗n0​+1∗n1​+2∗n2​+3∗n3​.
联立两个方程求解,可以得到 n 0 = 6 n_0=6 n0​=6

  1. 设森林F中有三棵树,第一,第二,第三棵树的结点个数分别为M1,M2和M3。与森林F对应的二叉树根结点的右子树上的结点个数是( )。

A. M1

B. M1+M2

C. M3

D. M2+M3
选D
根据森林转换为二叉树的法则,二叉树的根结点通常是第一棵树的结点,二叉树的左子树是由第一棵树删去根后所得所有子树构成的,二叉树的右子树是由其它树(第二，第三棵树)构成的,故左子树结点个数是M1-1,右子树上的结点个数是M2+M3。

  1. 具有10个叶结点的二叉树中有( )个度为2的结点,

A. 8

B. 9

C. 10

D. 11
选B
性质3：*对任何一棵二叉树，若它含有 n 0 n_0 n0​个叶子结点、 n 2 n_2 n2​个度为 2的结点，则必存在关系式 n 0 = n 2 + 1 n_0=n_2+1 n0​=n2​+1。
计算得 10 − 1 = 9 10-1=9 10−1=9

  1. 一棵完全二叉树上有1001个结点,其中叶子结点的个数是( )

A. 250

B. 500

C. 254

D. 505

E. 以上答案都不对
选E
方法一：由 性质4： *具有 n 个结点的完全二叉树的深度为: ⌊ log ⁡ 2 n ⌋ + 1 \lfloor\log_2 n\rfloor + 1 ⌊log2​n⌋+1 可得树高为 9 + 1 = = 10 9+1==10 9+1==10
前九层的总结点个数为 2 9 − 1 = 511 2^9-1=511 29−1=511
第十层的结点个数为 1001 − 511 = 490 1001-511=490 1001−511=490
第九层上结点个数为 2 9 − 1 = 256 2^{9-1}=256 29−1=256
第九层上叶节点个数为 256 − 490 / 2 = 11 256-490/2=11 256−490/2=11
因此叶节点一共有 490 + 11 = 501 ( 个 ) 490+11=501(个) 490+11=501(个)

方法二：
完全二叉树的最后一个结点的编号是 n n n，则它的父结点的编号为 [ n / 2 ] [n/2] [n/2]，则叶子结点个数为 n − [ n / 2 ] n-[n/2] n−[n/2]。
完全二叉树的最后一个结点的编号一定是1001，则它的父结点的编号为1001/2=500，则叶子结点个数为1001-500=501.

  1. 设给定权值总数有n 个,其哈夫曼树的结点总数为( )

A. 不确定

B. 2n

C. 2n+1

D. 2n-1
选 D
哈夫曼树中只有度为0和2的节点，且有此关系 n 0 = n 2 + 1 ( 度为 0 的节点个数 = 度为 2 的节点个数 + 1 ) n_0=n_2+1(度为0的节点个数=度为2的节点个数+1) n0​=n2​+1(度为0的节点个数=度为2的节点个数+1) 哈夫曼树中权值所在的节点一定是叶子节点，有哈夫曼树的构造决定的。
因此“给定权值总数有 n n n个”，也就是说叶子节点有 n n n个，则度为2的节点个数为 ( n − 1 ) (n-1) (n−1)，哈夫曼树总结点个数为 n + ( n − 1 ) = 2 n − 1 n+(n-1)=2n-1 n+(n−1)=2n−1
根据：
性质3：*对任何一棵二叉树，若它含有 n 0 n_0 n0​个叶子结点、 n 2 n_2 n2​个度为 2的结点，则必存在关系式 n 0 = n 2 + 1 n_0=n_2+1 n0​=n2​+1。

  1. 一个具有1025个结点的二叉树的高h为( )

A. 11

B. 10

C. 11至1025之间

D. 10至1024之间
选A
由
性质4： *具有 n 个结点的完全二叉树的深度为: ⌊ log ⁡ 2 n ⌋ + 1 \lfloor\log_2 n\rfloor + 1 ⌊log2​n⌋+1 可得树高为 10 + 1 = = 11 10+1==11 10+1==11

  1. 一棵二叉树高度为h,所有结点的度或为0,或为2,则这棵二叉树最少有( )结点

A. 2h

B. 2h-1

C. 2h+1

D. h+1
选B
性质3：*对任何一棵二叉树，若它含有 n 0 n_0 n0​个叶子结点、 n 2 n_2 n2​个度为 2的结点，则必存在关系式 n 0 = n 2 + 1 n_0=n_2+1 n0​=n2​+1。
在这里插入图片描述

  1. 一棵树高为K的完全二叉树至少有( )个结点

A. 2 k – 1 2^k –1 2k–1

B. 2 k − 1 – 1 2^{k-1} –1 2k−1–1

C. 2 k − 1 2^{k-1} 2k−1

D. 2 k 2^k 2k
选C
至少的情况：最后一层只有一个叶子结点，前 K-1 层是满二叉树。因此，结点数可以通过以下公式计算： [ 至少结点数 = 2 ( K − 1 ) − 2 ( K − 1 ) + 1 = 2 K − 2 ( K − 1 ) ] [ \text{至少结点数} = 2^{(K-1)} - 2^{(K-1)} + 1 = 2^{K} - 2^{(K-1)} ] [至少结点数=2(K−1)−2(K−1)+1=2K−2(K−1)]
至多的情况：第 K 层是满二叉树，因此结点数最多为： [ 至多结点数 = 2 K − 1 ] [\text{至多结点数} = 2^{K} - 1 ] [至多结点数=2K−1]

完全二叉树：

    1.  完全二叉树：树中所含的 n个结点和满二叉树中编号为 1 至 n 的结点一一对应。
     2.  特点：结点没有左孩子一定没有右孩子；度为1的结点最多有一个

  • 1
  • 2

性质1：二叉树的第 i层上至多有 2 i − 1 2^{i-1} 2i−1个结点 ( i ≥ 1 ) (i≥1) (i≥1)。
性质2：深度为k的二叉树上至多含 ( 2 k − 1 ) (2^k-1) (2k−1)个结点 ( k ≥ 1 ) (k≥1) (k≥1)。达到最多的时候，就是满二叉树。
性质3：*对任何一棵二叉树，若它含有 n 0 n_0 n0​个叶子结点、 n 2 n_2 n2​个度为 2的结点，则必存在关系式 n 0 = n 2 + 1 n_0=n_2+1 n0​=n2​+1。

  1. 一棵二叉树的前序遍历序列为ABCDEFG,它的中序遍历序列可能是( )

A. CABDEFG

B. ABCDEFG

C. DACEFBG

D. ADCFEG
选B
当二叉树所有节点都只有有右孩子时，选项中只有B成立。

  1. 下面的说法中正确的是( ).
    (1)任何一棵二叉树的叶子结点在三种遍历中的相对次序不变;
    (2)按二叉树定义,具有三个结点的二叉树共有6种。

A. (1)(2)

B. 1

C. 2

D. (1)、(2)都错
选B
(1)是正确的 解析看第15题。任何一颗二叉树的叶子结点在先序、中序、后序遍历序列中的相对次序是不发生改变的
(2)应该是五种.
在这里插入图片描述

  1. 在二叉树结点的先序序列,中序序列和后序序列中,所有叶子结点的先后顺序( )

A. 都不相同

B. 完全相同

C. 先序和中序相同,而与后序不同

D. 中序和后序相同,而与先序不同
选B

  • 前序遍历序列的顺序是根节点 --> 左子树 --> 右子树；
  • 后序遍历序列的顺序是左子树 --> 右子树 --> 根结点；
  • 中序遍历序列的顺序是左子树 --> 根结点 --> 右子树；
    因此相对次序发生变化的都是子树的根，也就是非叶结点。 所以各叶子之间的相对次序关系在前序序列、中序序列和后序序列中是一样的。
  1. 某二叉树的前序序列和后序序列正好相反,则该二叉树一定是()的二叉树。

A. 空或只有一个结点

B. 任一结点无左子树

C. 高度等于其结点数

D. 任一结点无右子树
选C
高度等于其结点个数的二叉树，即任意结点只有左孩子或只有右孩子，前序序列即从上向下的层序，后序序列即从下向上的层序。

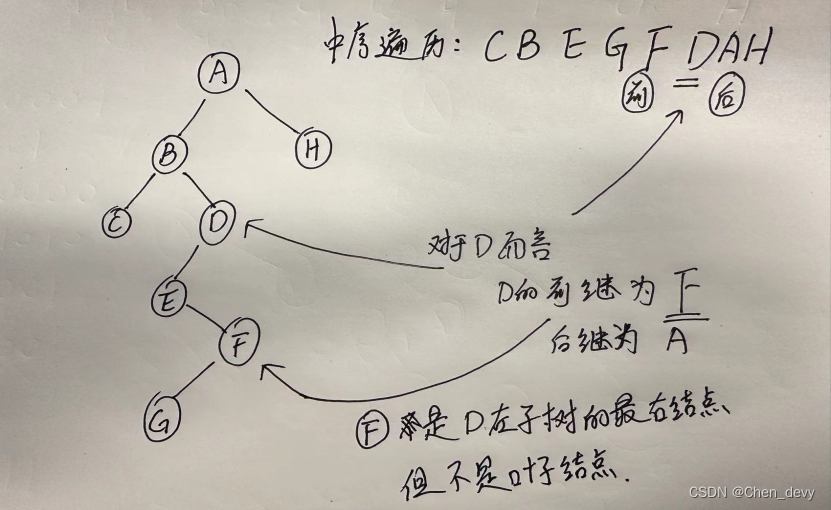
  1. 若X是二叉中序线索树中一个有左孩子的结点,且X不为根,则x的前驱为( )

A. X的双亲

B. X的右子树中最左的结点

C. X的左子树中最右结点

D. X的左子树中最右叶结点
正确答案：C
在这里插入图片描述

  1. 引入二叉线索树的目的是( )

A. 加快查找结点的前驱或后继的速度

B. 为了能在二叉树中方便的进行插入与删除

C 为了能方便的找到双亲

D. 使二叉树的遍历结果唯一
选A 加快查找结点前驱和后继的速度

  1. n个结点的线索二叉树上含有的线索数为( )

A. 2n

B. n-1

C. n+1

D. n
选C
一个有n个节点的线索二叉树，每个节点都有指向左右孩子的两个指针域，则共有2n个指针域，而n个节点共有n-1条分支，所以共有2n-(n-1)个空指针域，即有n+1个线索.

  1. 下述编码中哪一个不是前缀码( )。

A. (00,01,10,11)

B. (0,1,00,11)

C. (0,10,110,111)

D. (1,01,000,001)
选B
0是00的前缀 1是11的前缀

二、算法设计题

判断二叉树是否为完全二叉树

  1. 判断二叉树是否为完全二叉树

判断二叉树是否为完全二叉树的函数：

//完全二叉树的性质
bool check(BiTree T){
    if((T->lchild && T->rchild)||(!T->lchild && !T->rchild))
        return true;
    return false;
}       


//判断是否的完全二叉树
bool is_Complete_Binarytree(BiTree T){
    BiTree p=T;
    SqQueue Q;
    if(!T) return true;//空树也是完全二叉树
    InitQueue(Q);
    EnQueue(Q,p);
    while(!is_QueueEmpty(Q)){
        DeQueue(Q,p);
        if(!check(p)) return false;
        else{
            if(p->lchild) 
                EnQueue(Q,p->lchild);
		    if(p->rchild) 
                EnQueue(Q,p->rchild);
        }
    }
    return true;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27

(带main函数)题解代码示例：

//给定一个二叉树，找出其最小深度。
//最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

#include<iostream>
using namespace std;


//判断二叉树是否为完全二叉树

//结点定义入下：
//二叉链表
typedef struct BiTNode{
    char data;
    struct BiTNode *lchild,*rchild;
} BiTNode, *BiTree;

//若用到队列，请用循环队列，并请实现队列的相关操作以供调用。

#define MAXQSIZE 100

typedef struct {
    BiTree *base;
    int front,rear;
} SqQueue; //定义循环队列


//二叉树的建立的算法(按先序遍历序列建立)
void CreateBiTree(BiTree &T) {
	char ch; 
    scanf("%c",&ch);
    if (ch=='#') T = NULL;
    else {
        T = (BiTNode*)malloc(sizeof(BiTNode));
        T->data = ch;      // 生成根结点
        CreateBiTree(T->lchild); // 构造左子树
        CreateBiTree(T->rchild); // 构造右子树
    }
}
//队列的初始化
void InitQueue(SqQueue &Q){
    Q.base = (BiTree *)malloc(MAXQSIZE*sizeof(BiTree));
    Q.front = Q.rear = 0;//队列初始化
}

//队空
bool is_QueueEmpty(SqQueue Q){
    if(Q.rear==Q.front) return true;
    return false;
}

//队满
bool is_QueueMAX(SqQueue Q){
    if((Q.rear+1)%MAXQSIZE == Q.front) return true;
    return false;
}


//入队
void EnQueue(SqQueue &Q,BiTree e){
    if(!is_QueueMAX(Q)){
        Q.base[Q.rear]=e;
        Q.rear = (Q.rear + 1) % MAXQSIZE;
    }
    
    else{
        cout<<"ERROR!!! 队列已满"<<endl;
    }
}
//出队
void DeQueue(SqQueue &Q,BiTree &e){
    if(!is_QueueEmpty(Q)){
        e = Q.base[Q.front];
        Q.front = (Q.front + 1) % MAXQSIZE;
    }
    else{
        cout<<"ERROR!!! 队列为空"<<endl;
    }
}

//完全二叉树的性质
bool check(BiTree T){
    if((T->lchild && T->rchild)||(!T->lchild && !T->rchild))
        return true;
    return false;
}       


//判断是否的完全二叉树
bool is_Complete_Binarytree(BiTree T){
    BiTree p=T;
    SqQueue Q;
    if(!T) return true;//空树也是完全二叉树
    InitQueue(Q);
    EnQueue(Q,p);
    while(!is_QueueEmpty(Q)){
        DeQueue(Q,p);
        if(!check(p)) return false;
        else{
            if(p->lchild) 
                EnQueue(Q,p->lchild);
		    if(p->rchild) 
                EnQueue(Q,p->rchild);
        }
    }
    return true;
}

//层次遍历算法 
void LevelOrderTraverse(BiTree T)
{	BiTree p = T;
	SqQueue Q;
	
	
	if(!T) return;	
	
	InitQueue(Q); EnQueue(Q,p);
	while (!is_QueueEmpty(Q))
	{	DeQueue(Q,p);
		printf("%c ", p->data);
		if(p->lchild) EnQueue(Q,p->lchild);
		if(p->rchild) EnQueue(Q,p->rchild);
	}
}




int main(){
	 
	BiTree T;
	//例如输入：ABC##DE##F### 来创建二叉树 
	CreateBiTree(T);
    LevelOrderTraverse(T);
    cout<<endl;
    if(is_Complete_Binarytree(T)){
        cout<<"是完全二叉树"<<endl;
    }
    else{
        cout<<"不是完全二叉树"<<endl;
    }
	

	return 0; 
} 


  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90
  • 91
  • 92
  • 93
  • 94
  • 95
  • 96
  • 97
  • 98
  • 99
  • 100
  • 101
  • 102
  • 103
  • 104
  • 105
  • 106
  • 107
  • 108
  • 109
  • 110
  • 111
  • 112
  • 113
  • 114
  • 115
  • 116
  • 117
  • 118
  • 119
  • 120
  • 121
  • 122
  • 123
  • 124
  • 125
  • 126
  • 127
  • 128
  • 129
  • 130
  • 131
  • 132
  • 133
  • 134
  • 135
  • 136
  • 137
  • 138
  • 139
  • 140
  • 141
  • 142
  • 143
  • 144
  • 145

求二叉树的最小深度 以及 二叉树树高

  1. 求二叉树的最小深度
    给定一个二叉树，找出其最小深度。
    最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

求二叉树的最小深度的函数：

//直接就是将求树高的程序进行修改，将找左右子树最大树高 改为求左右子树 最小树高
//求二叉树的最小深度
int Get_minHeigt(BiTree T){
    //二叉树的最小深度
    if(T==NULL) return 0;
    else{
        int Left_Height = Get_minHeigt(T->lchild);
        int Right_Height = Get_minHeigt(T->rchild);
        int Tree_minHeight = 1+(Left_Height < Right_Height?Left_Height:Right_Height);//取最短路径
        return Tree_minHeight;
    }

}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13

(带main函数)题解代码示例：

//给定一个二叉树，找出其最小深度。
//最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

#include<iostream>
using namespace std;


typedef struct TreeNode{
	int data;//数据域
	TreeNode *rchild;//右孩子指针
	TreeNode *lchild;//左孩子指针
}TreeNode, *BiTree;


//二叉树的建立的算法(按先序遍历序列建立)
void CreateBiTree(BiTree &T) {
	char ch; 
    scanf("%c",&ch);
    if (ch=='#') T = NULL;
    else {
        T = (TreeNode*)malloc(sizeof(TreeNode));
        T->data = ch;      // 生成根结点
        CreateBiTree(T->lchild); // 构造左子树
        CreateBiTree(T->rchild); // 构造右子树
    }
}


//求树高 
int Get_Height(BiTree node){//递归 求树高 
	if(node==NULL) return 0;
	else{
		int Left_Height = Get_Height(node->lchild);
		int Right_Height = Get_Height(node->rchild);
		int Tree_Height = 1 + (Left_Height > Right_Height?Left_Height:Right_Height);//计算树高
    	return Tree_Height;
	}
	
}
//求二叉树的最小深度
int Get_minHeigt(BiTree T){
    //二叉树的最小深度
    if(T==NULL) return 0;
    else{
        int Left_Height = Get_minHeigt(T->lchild);
        int Right_Height = Get_minHeigt(T->rchild);
        int Tree_minHeight = 1+(Left_Height < Right_Height?Left_Height:Right_Height);//取最短路径
        return Tree_minHeight;
    }

}


int main(){
	 
	BiTree T;
	//例如输入：ABC##DE##F### 来创建二叉树 
	CreateBiTree(T);

	cout<<"树高为：" ;
	cout<<Get_Height(T)<<endl;
    cout<<"根节点到叶节点的最短路径上的节点数量为：";
    cout<<Get_minHeigt(T)<<endl;

	return 0; 
} 


  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67

感谢阅读！！！

  1. 树与二叉树知识点文章: 【数据结构】树与二叉树（递归法先序、中序、后序、层次遍历二叉树、二叉树的建立以及求树高的方法）
  2. 二叉树遍历算法的应用: 【数据结构】树与二叉树遍历算法的应用（求叶子节点个数、求树高、复制二叉树、创建二叉树、二叉树存放表达式、交换二叉树每个结点的左右孩子）
  3. 树与森林知识点文章: 【数据结构】树与森林（树的存储结构、森林与二叉树的转化、树与森林的遍历）
声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/我家小花儿/article/detail/439804
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号