双臂二指魔方机器人的制作（三）--还原控制_双臂魔方机器人 算法优化

本文素材来源于广西大学 机械工程学院

作者：孙尹同  黄祖杰

指导老师：李俚

       魔方还原算法最早可以追溯到1980年捷克共和国的女大学生 Jessica Fridrich 发明的 CFOP 算法，目前这个算法仍然广泛应用于国际魔方速拧比赛中。而经过几十年的发展，魔方还原的主流算法有:层先法、角先法、TM算法和二阶段算法。关于算法的优劣与否，主要看它的两个方面：魔方还原步数、魔方寻优时间。本文算法追求的是在尽可能短的时间内完成魔方的还原。双臂二指魔方机器人还原魔方的时间包括寻优的时间和机器人拧魔方的时间，而双臂二指魔方机器人完成一次魔方旋转所用的时间是固定的，因此机器人还原魔方的时间与还原指令的长度呈线性关系，即还原指令长度越短，魔方还原所花费的时间越少。根据相关资料显示，Kociemba 二阶段算法是最优的选择。本章主要介绍Kociemba 二阶段算法。

1.魔方状态分析

      魔方的状态分析是实现魔方成功求解的前提和基础。如果把魔方的12个棱块放于12个边的位置，根据排列顺序有12!种情况，除此之外，还要考虑棱块的方向问题，有2种方向置于12个边上，根据乘法原理可知有 种情况，综上所述棱块的状态数一共有：

 

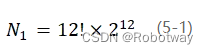
       同理，魔方有8个角块，每个角块朝向有3种，所以角块的状态数一共是：

 

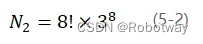
       然而，魔方的一些状态是不存在的。因为对于一个还原的魔方来说，不存在单独改变一个棱块或角块的朝向的情况以及单独一对角块和一对棱块互换位置的情况[37]，所以应该在魔方所有状态的基础上去掉一个倍数：

 

此可以得到魔方的所有可能状态数：

 

由此得到:

       魔方的所有可能状态有43252003274489856000种，说明魔方还原的难度非常之大，想要通过胡乱的旋转侥幸将魔方还原是几乎不可能的。因此各种各样的魔方还原算法接踵而来，目前人们已经将“上帝之数”压缩到20，即任何一种组合的魔方都能在20步以内还原。

2. Kociemba 二阶段算法

       经上位机（电脑）视觉识别处理完成之后，就得到一串包含魔方相对位置与颜色的字符串，这串字符串就代表了这个魔方此时的状态信息，通过这串字符串，计算机也就可以准确的得到此时的魔方模型状态。目前来说，魔方机器人使用较为广泛的算法是来自 Kociemba 的二阶段算法，以下简称 Kociemba 算法。Kociemba 算法是一种能在较短时间内使用较短步数还原魔方的算法，通常能在 1s 内得到平均 20 步的解法，相比较于人工还原魔方的方法，如层先法、角先法，进阶的如 CFOP 法的动辄上百步还原步骤，是非常具有优势的， 所以我们也采用的此算法。

       我们可以把魔方简单的看做一个立方体，对每个面进行相应的标记，六个面分我们可以把魔方简单的看做一个立方体，对每个面进行相应的标记分别为 U（顶面）、F（前面）、 L（左面）、R（右面）、B（后面）、D（下面），对于每一个面，又分别有顺时针旋转 90°，逆时针旋转 90°， 旋转 180°（顺时针逆时针均可）这三种操作，我们可以把对应的操作记为 XY，其中 X 为面的代号，Y 为对 应操作代号（1 为顺时针旋转 90°，2 为旋转 180°，3 逆时针旋转 90°），如 U3 就代表着是顶层逆时针旋转 90°。经 Kociemba 算法得到的解法就是多个上述操作代号相连起来，例如“D2 R1 D3 F2 B1 D1 R2 D2 R3 F2 D3 F2 U3 B2 L2 U2 D1 R2 U1”就是经 Kociemba 算法得出来的完整的一个解魔方步骤。

3.魔方转动状态分析

 

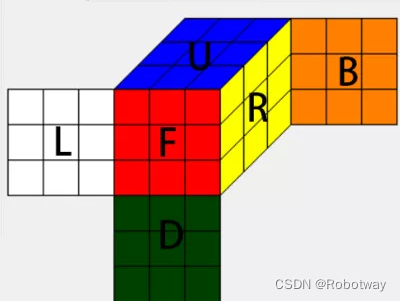
       我们可以把魔方简单的看做一个立方体，对每个面进行相应的标记，六个面分别为U(顶面)、F（前面）、L（左面）、R（右面）、B（后面）、D（下面），对于每一个面，又分别有顺时针旋转90°，逆时针旋转90°，旋转180°（顺时针逆时针均可）这三种操作，我们可以把对应的操作记为XY，其中X为面的代号，Y为对应操作代号（1为顺时针旋转90°，2为旋转180°，3逆时针旋转90°），如U3就代表着是顶层逆时针旋转90°。

4. kociemba算法结果

       经Kociemba算法得到的解法就是多个上述操作代号相连起来，例如“D2 R1 D3 F2 B1 D1 R2 D2 R3 F2 D3 F2 U3 B2 L2 U2 D1 R2 U1”就是经Kociemba算法得出来的完整的一个解魔方步骤。对于我们的机器人而言，这样的一个步骤是不能直接运用的，对于双臂二指机器人而言，如图，它能直接转动的面只有D、B两个面，要想转动其他的面，还需要进行一些其他的机械臂的操作转化，接下来会在下位机算法中详细介绍。

 

5. 串口通讯

       经Kociemba算法得到的解法，需要经过一定的通讯手段，将数据从上位机传输给下位机进行后续的操作，故选择简单并且稳定的usb串口通讯，只需要将上位机和下位机通过一根usb线连接起来，选取和下位机相对应的端口号和波特率，就可以向下位机传输这一组数据了，下附python源代码，其中的txt便是经Kociemba算法得到的一串包含正确解法的字符串。 

 6. 串口数据接收及数据解码

       下位机进行串口缓存检测，一旦有数据输入时，就按顺序读取单个字符值，并转化为字符，循环赋值给a数组。这样就可以得到上位机传输过来的数据了。

       但这样得到的字符串并不能被下位机直接识别，将得到的字符串以空格为界，将两个空格之间的字符的ASCLL码相加，使得魔方的每一个转动方式都有一个对应的十进制数字与之相对应。 

7. 机械臂控制及转化算法

       我们的双臂二指机器人包含两个舵机，分别控制左右两只手手指的夹紧与放开，另外还包含两个步进电机，用来分别控制左右两个机械臂的转动，我们可以做如下定义：

      L0左手手指张开

      L1左手手指夹紧

      Ls左手顺时针旋转90°

      Ln左手逆时针旋转90°

      L180左手旋转180°（至于是顺时针还是逆时针之后会有另行说明）

舵机控制代码： 

       步进电机在转动的时候，根据手指的夹紧和张开状态，有三种速度可以选择，在不同负载下选择不同的速度来进行转动，其中lim值的作用在下文防缠绕算法中会详细说明：

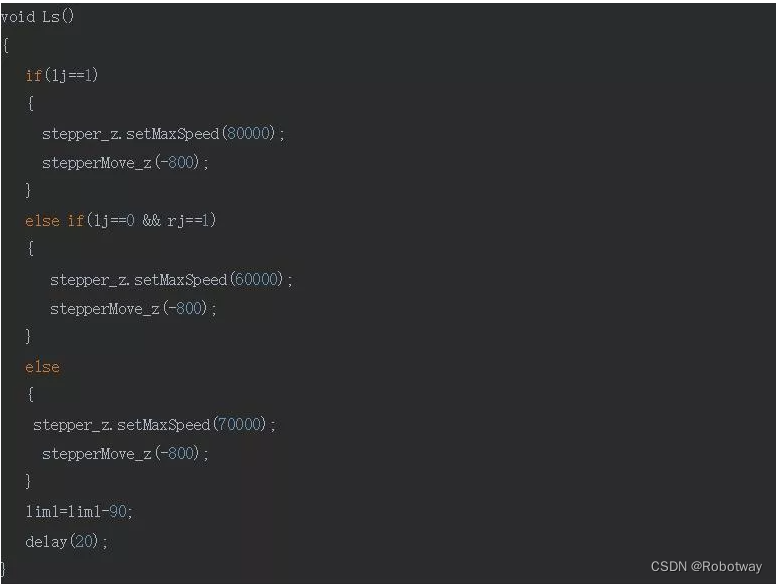
       R0、R1、Rs、Rn、R180则是右手相应动作。

       这样，我们就可以把魔方还原的解法通过一定的映射，转换为机器人相应的机械步骤，从而让机器人可以正确还原魔方。定义机械臂手指平行地面为归位，垂直地面为不归位，在进行一次转动操作以后，一共会出现三种状态，分别是1：左手归位、右手不归位2：左手不归位、右手归位3：左右手都归位。如在左右手臂都是初始状态时执行U3步骤：R1→L180→R0→Rn，对于其他步骤，同样存在相应的转化方法，下附表1。

 

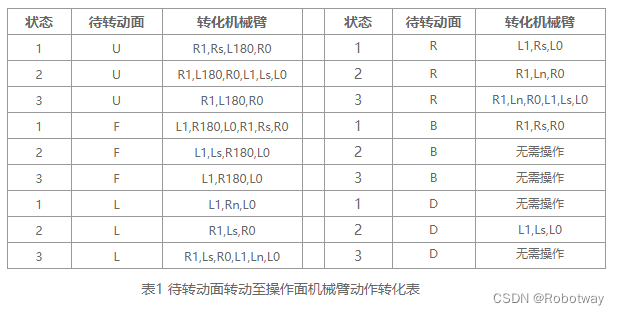
       经过这样的操作之后，只是把待转动面移动到了机械爪的操作范围之内，至于是顺时针还是逆时针，用左手还是右手，经过程序的进一步判断以后就可以进行下一步操作。

8. 坐标转换算法

       当然，在双手机械臂还原魔方的过程中，会涉及到一定的坐标变换，如执行U3步骤之后，后续的所有还原步骤中：U→D、D→U、L→R、R→L，F和B面不变，不难发现，只要是对U面进行操作，都是这样的坐标转换步骤。当然，对于其他另外的5个面，在进行操作以后也会有一定的转换规则，下附表2。

 

9.步进电机控制

       当步进电机加速度过快时，会使魔方发生错位的风险，在这里，通过使用了Arduino自带的AccelStepper库函数，可以更加简单方便的来驱动步进电机来达到想要的速度。

10.线的防缠绕算法

       由于机器人选择的是用舵机来控制手指的开合，在舵机和控制板之间必须要有一根线来传输数据和提供电力，在魔方进行还原的过程中，如果不加以限制，这根线就会一点一点的缠绕在机械臂上，为了解决这个问题，我们做了如下优化工作：定义机器人初始机械臂状态为“0”，当机械臂顺时针旋转90°后，我们让机械臂状态值加上90，逆时针旋转90°则减去90，在之前定义旋转180°的时候，我们没有定义旋转的方向，在这里，我们可以根据状态值动态选择顺时针还是逆时针，具体来说，就是在机械臂要进行旋转180°的时候，机械臂状态值大于0时，选择逆时针旋转180°，同时状态值减少180，状态值小于0时，选择顺时针旋转180°，同时状态值加上180，这样的算法会使机械臂在旋转的过程中，机械臂的状态值始终是趋近于0也就是机械臂的状态始终向着初始状态靠近，这样就可以解决线的缠绕问题。 

       在经过这样的一系列算法处理以后，魔方机器人就可以驱动电机，实现还原魔方的操作了。

       通过 10 次的平稳运行测试，还原速度在 18s~25s 区间内，平均还原速度为 22.9 s。

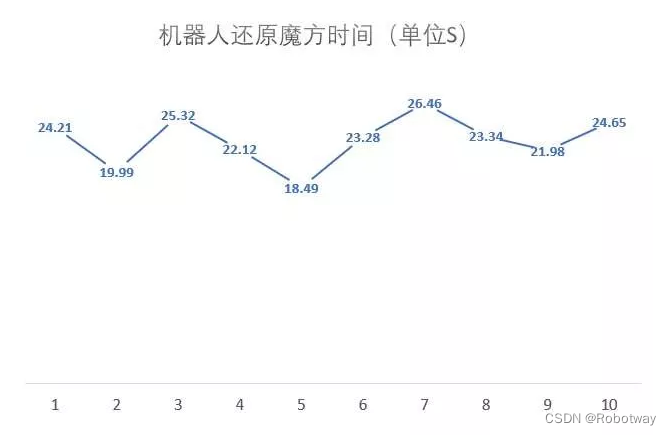
关于双臂二指魔方机器人的详细内容可参考双臂二指魔方机器人

-----------------------------------------------完结---------------------------------------------------