- 1JVM垃圾回收--垃圾回收器--CMS和G1的区别和执行流程_g1 和cms 卡表的区别
- 2基于大数据的宠物领养系统设计与实现 毕业论文+任务书+开题报告+毕业设计方案+中期答辩PPT+毕业答辩PPT+答辩稿+项目源码及数据库文件+演示视频+指导视频_毕设宠物管理系统的中期报告
- 3低成本DIY空气质量检测仪(D1 Mini ESP8266<Tasmota固件> 、PMS5003)_d1 mini esphome
- 4用D3.js绘制完整的流程图demo_d3.js demo
- 5探索ChatGPT Web Share:利用AI的力量进行智能对话与创作
- 6JavaScript快速入门-基础_javascrip快速入门文档
- 7可视化数据分析-基于JavaScript的d3实践学习_d3 javascript
- 8【Paddle】PCA线性代数基础 + 领域应用:人脸识别算法(1.1w字超详细:附公式、代码)_paddle 人脸识别
- 9【信息安全案例】——信息内容安全(学习笔记)
- 10实用AI工具分享|平替 ChatGPT,帮助效率提高
随机森林分类、回归、调参、特征重要性_随机森林特征重要性
赞
踩
一、基本概念
随机森林(RF)是一种组合分类器,它利用 bootstrap 重抽样方法从原始样本中抽取多个样本,对每个 bootstrap 样本进行决策树建模,然后将这些决策树组合在一起,通过投票得出最终分类或预测的结果。大量的理论和实证研究都证明了随机森林算法具有较高的预测准确率,对异常值和噪声具有很好的容忍度,且不容易出现过拟合。
(一)决策树的不足
1.分类规则复杂,一般采用剪枝的办法实现。
2.ID3算法,在选择了一个属性后,不再会朔重新考虑这个选择,容易造成局部最优
3.容易过拟合
为了克服决策树的上述缺点,结合单个分类器组合成多个分类器的思想,这就是随机森林的核心思想。
(二)随机森林的构造步骤
1.为每棵树产生训练集,有放回抽样和不放回抽样,有放回抽样分为无权重抽样和更新权重抽样。无权重抽样,也叫bagging方法,boosting方法也叫更新权重抽样。
2.构建每棵决策树。构造每棵决策树涉及两个重要过程,节点分裂和随机特征的随机选取。现在的节点分裂原则一般都是选C4.5(信息增益率)或CART(基尼系数)。特征的随机选取主要是训练集随机选取,和特征随机选取。
(三)随机森林的优缺点
优点:实现简单,泛化能力强;相比单一的决策树,能学习到特征之间的相互影响,且不容易过拟合;相比SVM,不是很怕特征缺失;训练完成可以给出特征重要性,这个优点主要来源于决策树
缺点:在噪声过大的分类和处理回归问题时还是容易过拟合;相比单一的决策树,他的随机性,让我们难以对模型结果解释。
二、python实例
(一)手写数字识别
- #导入必要的包
- from sklearn.ensemble import RandomForestClassifier
- from sklearn.datasets import load_digits
- from sklearn.model_selection import train_test_split,GridSearchCV,cross_val_score
- from sklearn.metrics import accuracy_score
- import matplotlib.pyplot as plt
- import numpy as np
-
- #导入数据集
- data = load_digits()
- x = data.data
- y = data.target
- RF = RandomForestClassifier(random_state = 66)
- score = cross_val_score(RF,x,y,cv=10).mean()
- print('交叉验证得分: %.4f'%score)
创建一个随机森林分类器对象RF,并设置了随机种子为66。这里解释一下随机种子的含义:通过固定的种子值,我们可以确保每次运行程序时,得到相同的随机数序列。原理:在计算中,真正的随机数很难生成,通过使用伪随机数生成器来生成看似随机的数值。伪随机数生成器是根据一个初始种子值来生成随机数序列的。如果使用相同的种子值,伪随机数生成器将生成相同的随机数序列。
通过cross_val_score函数随机森林分类器进行交叉验证,cross_val_score函数是用于评估模型性能的函数,它会自动将数据集分成多个子集,这里是10个子集,然后用不同的子集作为训练集和测试集进行多次模型训练和评估,最后返回每次评估的得分。交叉验证结果为0.946。
- #训练一个模型,让oob_score=True
- RF1 = RandomForestClassifier(n_estimators=25,oob_score=True)
- RF1 =RF1.fit(x,y)
- #查看oob_score_,即袋外误差
- RF1.oob_score_
训练模型,设置25棵树,计算袋外误差。解释一下袋外数据的概念:有放回抽样,每个样本被抽到的概率是1/n,所以不被抽到的概率是1-1/n,所以n个样本都不被抽到的概率就是:(1-1/n)^n,用洛必达法则化简,这个概率收敛到1/e,约等于0.37。因此,数据量足够大时,约有37%的数据浪费掉,被称为袋外数据(out of bag data,简称oob)为了使他们不被浪费掉,我们可以用它来当测试集,也就是说,随机森林可以不划分测试集和训练集。当然,这需要样本数据n和n_estimators都很大,数据集过少,可能没有袋外数据。
手动调参--重要参数:
1. max_features:这个参数来控制训练每棵树选取的样本数,默认为auto。可填入的值有int值,float(特征总数目的百分比)等,默认值为总特征数开平方取整数,这个参数使得训练每棵树时只用到部分特征,抽样的随机性。
2. n_estimators:随机森林生成决策树的数量,默认值为100。
3. bootstrap:每次抽样是不是采取有放回抽样,可选参数:True和False 默认True,bootstrap为True时就会产生袋外数据。
4. oob_score:是否使用袋外数据来评估模型,默认False,如果希望使用袋外数据来测试,则需要将oob_score_参数调整为True。
5. max_samples:构建每棵树需要抽取的最大样本数据量,默认为None,即每次抽取的样本量和原数据量相同。
6. criterion:决策树划分标准规则
7. max_depth:每棵树的最大深度
8. min_samples_split:最小分裂样本数,拆分内部节点所需的最小样本数量
9. min_samples_leaf:最小叶子样本数
10. max_features:每棵树所选取的最大特征数量
调参:
1)选择criterion参数
- RF = RandomForestClassifier(random_state = 66)
- score = cross_val_score(RF,x,y,cv=10).mean()
- print('基尼系数得分: %.4f'%score)
- RF = RandomForestClassifier(criterion = 'entropy',random_state = 66)
- score = cross_val_score(RF,x,y,cv=10).mean()
- print('熵得分: %.4f'%score)
这里得到熵得分09488,基尼系数得分0.9460
2)探索n_estimators参数
- ###调n_estimators参数
- ScoreAll = []
- for i in range(10,200,10):
- DT = RandomForestClassifier(n_estimators = i,random_state = 66) #,criterion = 'entropy'
- score = cross_val_score(DT,data.data,data.target,cv=10).mean()
- ScoreAll.append([i,score])
- ScoreAll = np.array(ScoreAll)
-
- max_score = np.where(ScoreAll==np.max(ScoreAll[:,1]))[0][0] ##这句话看似很长的,其实就是找出最高得分对应的索引
- print("最优参数以及最高得分:",ScoreAll[max_score])
- plt.figure(figsize=[20,5])
- plt.plot(ScoreAll[:,0],ScoreAll[:,1])
- plt.show()
输出:
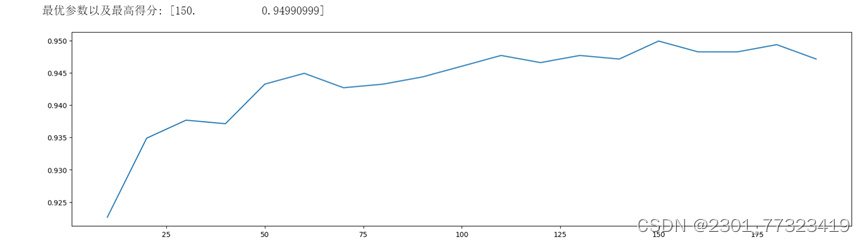
根据曲线,我们进一步缩小范围,搜索120~160之间的得分
- ###进一步缩小范围,调n_estimators参数
- ScoreAll = []
- for i in range(120,160):
- DT = RandomForestClassifier(n_estimators = i,random_state = 66) #criterion = 'entropy',
- score = cross_val_score(DT,data.data,data.target,cv=10).mean()
- ScoreAll.append([i,score])
- ScoreAll = np.array(ScoreAll)
-
- max_score = np.where(ScoreAll==np.max(ScoreAll[:,1]))[0][0] ##这句话看似很长的,其实就是找出最高得分对应的索引
- print("最优参数以及最高得分:",ScoreAll[max_score])
- plt.figure(figsize=[20,5])
- plt.plot(ScoreAll[:,0],ScoreAll[:,1])
- plt.show()
输出:
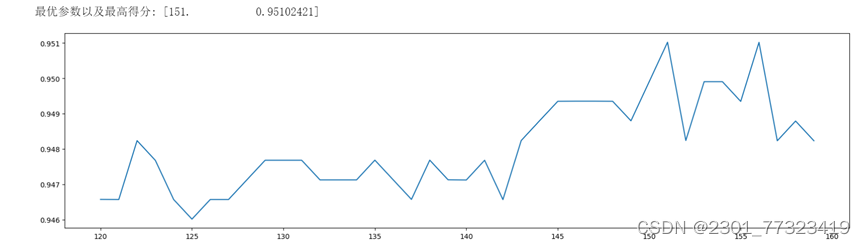
可以看出,151棵树为得分最高点,我们暂定n_estimators为151,接着调整下边的参数。
3)探寻max_depth(树的最大深度)
- ###粗调max_depth参数
- ScoreAll = []
- for i in range(10,30,5):
- DT = RandomForestClassifier(n_estimators = 151,random_state = 66,max_depth =i ) #,criterion = 'entropy'
- score = cross_val_score(DT,data.data,data.target,cv=10).mean()
- ScoreAll.append([i,score])
- ScoreAll = np.array(ScoreAll)
-
- max_score = np.where(ScoreAll==np.max(ScoreAll[:,1]))[0][0] ##这句话看似很长的,其实就是找出最高得分对应的索引
- print("最优参数以及最高得分:",ScoreAll[max_score])
- plt.figure(figsize=[20,5])
- plt.plot(ScoreAll[:,0],ScoreAll[:,1])
- plt.show()
输出:
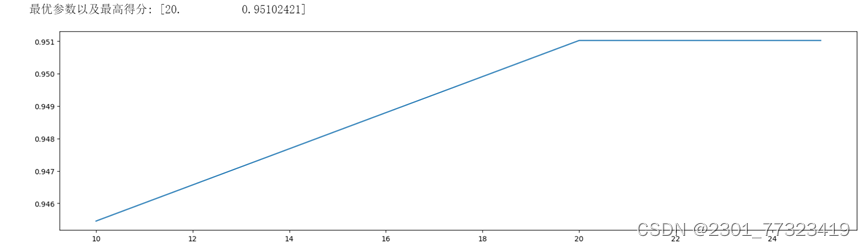
转折点在20,20滞后一直没有变化,可以说明就算不限制,所有树的最大深度也在20左右,因为我们是以5为步长的,所以还需进一步搜索一下16附近的值。精细搜索之后,发现,20这个值就是转折点,暂定max_depth=20。
4)探索min_samples_split的最优参数(节点最小分裂样本数量)
Min_samples_split最小值就是2,我们就从2开始调整。当一个节点中,样本数量小于min_samples_split时,决策树停滞拆分,该节点最为叶子结点。停止进一步分裂,这样可以防止过度拟合。
- ###调min_samples_split参数
- ScoreAll = []
- for i in range(2,8):
- RF = RandomForestClassifier(n_estimators = 151,random_state = 66,max_depth =20,min_samples_split = i ) #,criterion = 'entropy'
- score = cross_val_score(RF,data.data,data.target,cv=10).mean()
- ScoreAll.append([i,score])
- ScoreAll = np.array(ScoreAll)
-
- max_score = np.where(ScoreAll==np.max(ScoreAll[:,1]))[0][0] ##这句话看似很长的,其实就是找出最高得分对应的索引
- print("最优参数以及最高得分:",ScoreAll[max_score])
- plt.figure(figsize=[20,5])
- plt.plot(ScoreAll[:,0],ScoreAll[:,1])
- plt.show()
输出:
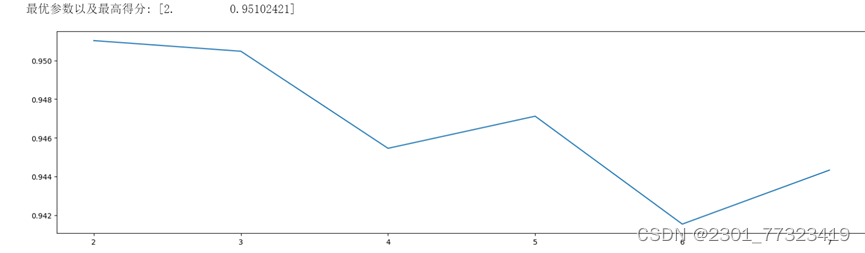
可以看到,随着min_samples_split增大,模型得分下降,说明没有出现过拟合现象,min_samples_split暂定为2。
5)探寻min_samples_leaf最佳参数
- ###调min_samples_leaf参数
- ScoreAll = []
- for i in range(1,10,2):
- DT = RandomForestClassifier(n_estimators = 151,random_state = 66,max_depth =20,min_samples_leaf = i,min_samples_split = 2 )
- score = cross_val_score(DT,data.data,data.target,cv=10).mean()
- ScoreAll.append([i,score])
- ScoreAll = np.array(ScoreAll)
-
- max_score = np.where(ScoreAll==np.max(ScoreAll[:,1]))[0][0] ##这句话看似很长的,其实就是找出最高得分对应的索引
- print("最优参数以及最高得分:",ScoreAll[max_score])
- plt.figure(figsize=[20,5])
- plt.plot(ScoreAll[:,0],ScoreAll[:,1])
- plt.show()
输出:
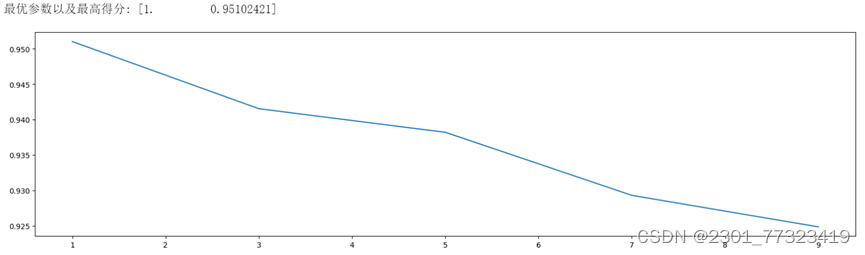 可以看到,随着min_samples_leaf增大,模型得分下降,说明没有出现过拟合现象,min_samples_leaf暂定为1。
可以看到,随着min_samples_leaf增大,模型得分下降,说明没有出现过拟合现象,min_samples_leaf暂定为1。
6)对每棵树用到的最大特征数调参(max_features):
正常来说,只要特征值不要设置的太小,所有特征都会被整个森林抽取到用来训练,所以相对来说这个值对整个模型的影响不是太大,但是这个值越大,单棵树需要考虑的特征越多,虽然模型的表现可能会更好,但是增加这个值对导致算法运行速度变慢,所以我们需要考虑去找一个平衡值。
- #调max_features参数
- param_grid = {
- 'max_features':np.arange(0.1, 1)}
-
- rfc = RandomForestClassifier(random_state=66,n_estimators = 151,max_depth =20,min_samples_leaf =1 ,min_samples_split =2 )
- GS = GridSearchCV(rfc,param_grid,cv=10)
- GS.fit(data.data,data.target)
- print(GS.best_params_)
- print(GS.best_score_)
结果显示,网格搜索中,找到的最佳max_features参数值为0.1,即每决策树只使用总特征数的0.1倍的特征进行训练。
此时我们得到的参数如下:
| 参数 | 值 |
| n_estimators | 151 |
| Max_depth | 20 |
| Min_samples_leaf | 1 |
| Min_samples_split | 2 |
| Max_features | 0.1 |
这个组合的准确率达到了95.269%比原来提高了0.329%
(二)随机森林回归问题
和决策树类似,随机森林同样分为分类森林和回归森林。
- import pandas as pd
- import matplotlib.pyplot as plt
- from sklearn.ensemble import RandomForestRegressor
- from sklearn.datasets import make_regression
- from sklearn.model_selection import train_test_split
- from sklearn.metrics import mean_squared_error
-
- # 创建一个回归数据集
- X, y = make_regression(n_samples=100, n_features=10, random_state=66)
首先使用make_regression函数生成一个具有10个特征的回归数据集。然后,使用train_test_split函数将数据集划分为训练集和测试集。
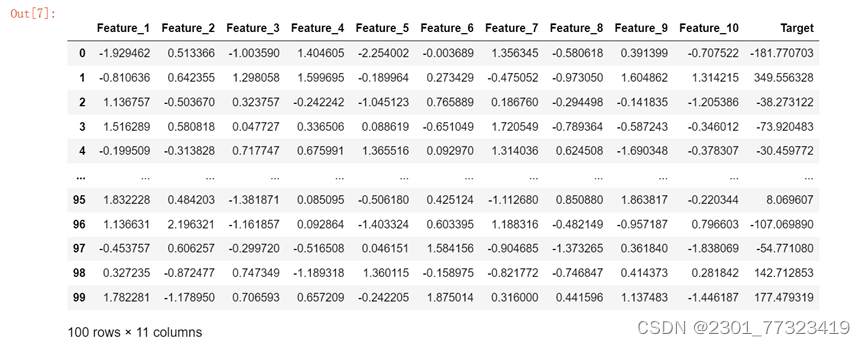
然后,使用训练集数据调用fit方法拟合模型。之后,使用测试集数据调用predict方法进行预测,得到预测结果y_pred。
最后,使用mean_squared_error函数计算实际值y_test和预测值y_pred之间的均方误差,评估模型的预测性能。
- # 将数据集划分为训练集和测试集
- X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=66)
-
- # 创建随机森林回归模型
- rf = RandomForestRegressor(n_estimators=100, random_state=66)
-
- # 在训练集上拟合模型
- rf.fit(X_train, y_train)
-
- # 在测试集上进行预测
- y_pred = rf.predict(X_test)
-
- # 计算均方误差(Mean Squared Error)
- mse = mean_squared_error(y_test, y_pred)
- print("均方误差(MSE):", mse)
(三)得到特征重要性
- # 获取特征重要性
- feature_importances = rf.feature_importances_
-
- # 创建一个DataFrame来存储特征重要性
- df_importance = pd.DataFrame({'Feature': [f"Feature_{i+1}" for i in range(X.shape[1])],
- 'Importance': feature_importances})
-
- # 按照特征重要性进行排序
- df_importance = df_importance.sort_values('Importance', ascending=False)
-
- # 绘制特征重要性条形图
- plt.figure(figsize=(10, 6))
- plt.bar(df_importance['Feature'], df_importance['Importance'])
- plt.xlabel('Features')
- plt.ylabel('Importance')
- plt.title('Feature Importance in Random Forest Regression')
- plt.xticks(rotation=45)
- plt.show()

输出:
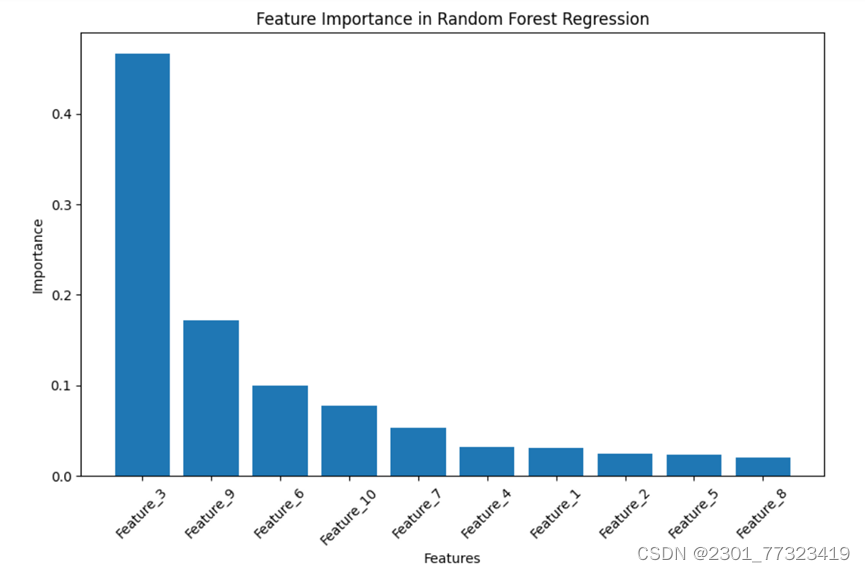
通过分析特征重要性,我们可以获得以下几个方面的信息:
1.特征选择:特征重要性可以帮助我们确定哪些特征对于预测目标变量最具有影响力。通过选择重要性较高的特征,可以简化模型并减少特征数量,提高模型的泛化能力和效果。
2.特征工程:特征重要性可以指导特征工程的过程。我们可以根据特征重要性的排序和比较,选择重要性较高的特征进行进一步的特征工程,例如特征组合、变量转换或衍生新特征。
3.可解释性:特征重要性提供了一种解释模型预测结果的方法。通过分析特征重要性,我们可以了解哪些因素对于模型预测的结果起到了主导作用。这对于理解问题领域的关键因素、发现潜在的影响因素以及解释模型的决策过程都是有帮助的。


